Ранговые коэффициенты корреляции • Для

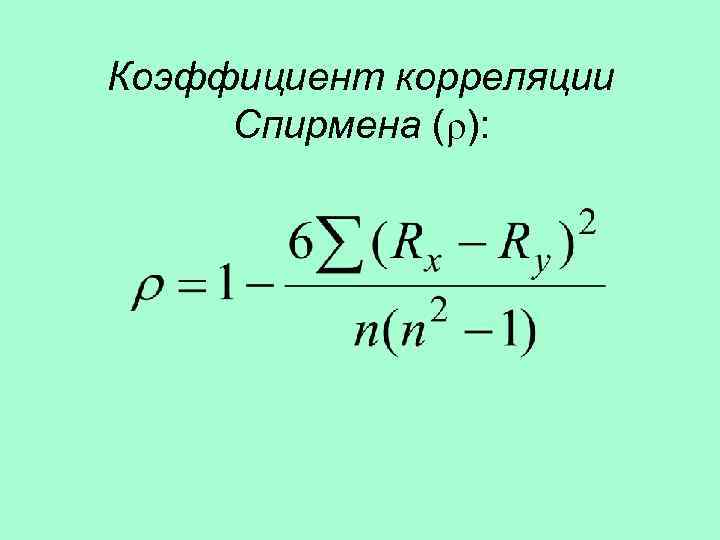
Ранговые коэффициенты корреляции

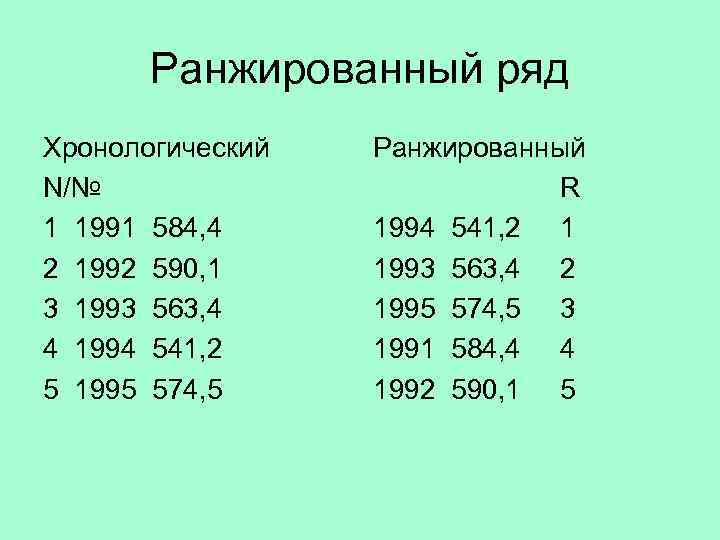
• Для измерения тесноты зависимости кроме перечисленных существуют так называемые ранговые коэффициенты корреляции. Когда коррелируют не сами значения показателей x и y, а их ранги, т. е. номера их мест, занимаемых в каждом ряду значений по возрастанию или убыванию. Ранги обозначают часто буквой R.

Ранжированный ряд Хронологический Ранжированный N/№ R 1 1991 584, 4 1994 541, 2 1992 590, 1 1993 563, 4 2 3 1993 563, 4 1995 574, 5 3 4 1994 541, 2 1991 584, 4 4 5 1995 574, 5 1992 590, 1 5

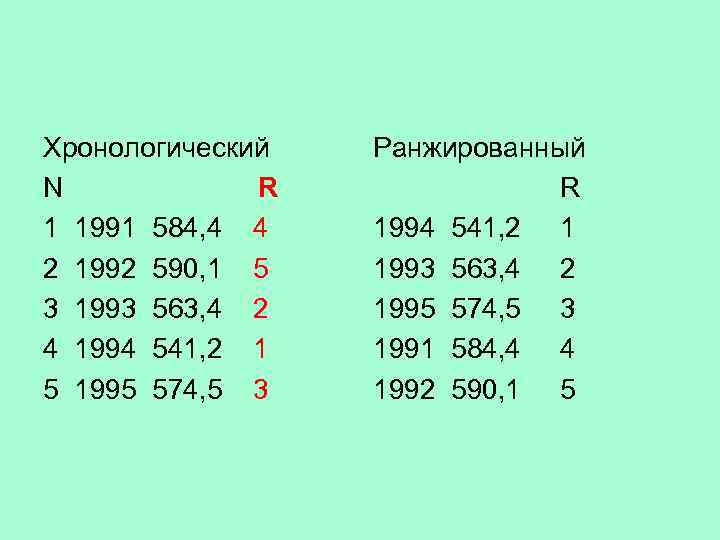
Хронологический Ранжированный N R 1 1991 584, 4 4 1994 541, 2 1992 590, 1 5 1993 563, 4 2 3 1993 563, 4 2 1995 574, 5 3 4 1994 541, 2 1 1991 584, 4 4 5 1995 574, 5 3 1992 590, 1 5

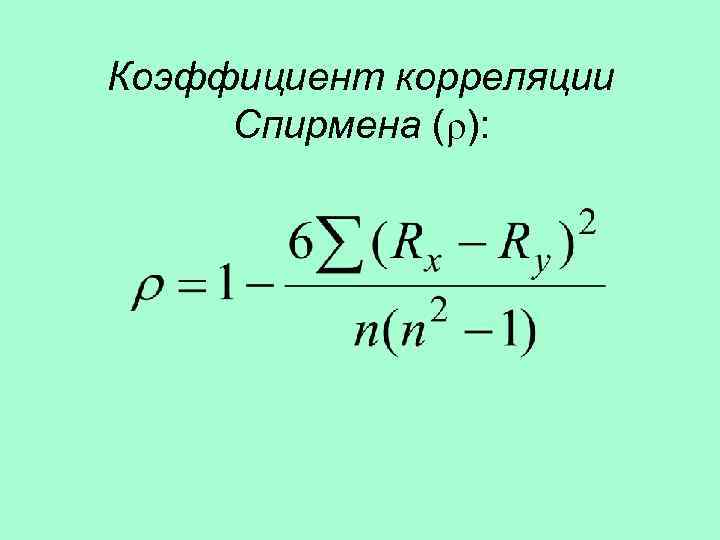Коэффициент корреляции Спирмена (ρ):

Коэффициент корреляции Кендела (τ):

Порядок расчета этих показателей следующий. • Значения x и y ранжируются, т. е. определяются Rx и Ry • Значения Rx записываются строго в порядке возрастания (или наоборот убывания) • Ранги второго показателя Ry располагаются в порядке соответствующем значению х в исходных данных.

• Для каждого значения Ry подсчитывается число следующих за ним рангов более высокого порядка. Общая сума таких случаев «правильного следования» последовательно для всех рангов учитывается как баллы со знаком «+» и обозначается символом Р.

• Аналогично для каждого значения Ry последователи подсчитывается, число следующих за ним рангов, меньших по значению. Общая сумма таких случаев (инверсий) учитывается как баллы со знаком «-» и обозначается символом Q. • Определяется общая сумма баллов, которая обозначается S, т. е. S= P+Q

Полученная сумма ( S ) сопоставляется с максимальной, которая равна в случае, если в обоих рядах ранги следуют строго последовательно от 1 до n.

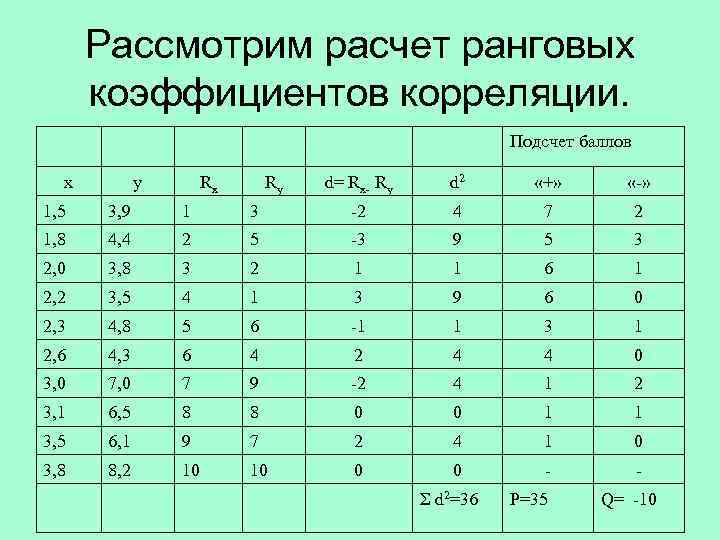
Рассмотрим расчет ранговых коэффициентов корреляции. Подсчет баллов x y Rx Ry d= Rx- Ry d 2 «+» «-» 1, 5 3, 9 1 3 -2 4 7 2 1, 8 4, 4 2 5 -3 9 5 3 2, 0 3, 8 3 2 1 1 6 1 2, 2 3, 5 4 1 3 9 6 0 2, 3 4, 8 5 6 -1 1 3 1 2, 6 4, 3 6 4 2 4 4 0 3, 0 7 9 -2 4 1 2 3, 1 6, 5 8 8 0 0 1 3, 5 6, 1 9 7 2 4 1 0 3, 8 8, 2 10 0 0 - - Σ d 2=36 Р=35 Q= -10

Коэффициент корреляции Спирмена (ρ):

Коэффициент корреляции Кендела (τ): Сначала определяем S. S= P+Q Подсчет баллов происходит следующим образом – после первой пары значений рангов, где Ry=3, в 7 случаях идут значения Ry>3 и в 2 случаях Ry<3 (1, 2), после второй пары R y =5, наблюдается 5 случаев выше рассматриваемого и 3 ниже. S= P+Q = 35 -10=25 τ=0, 44

Коэффициент Кендэла всегда меньше коэффициента Спирмена. Значения ранговых коэффициентов корреляции интерпретируется – чем ближе значение ρ или τ к 1, тем теснее зависимость, а близость к 0 означает отсутствие связи.

Коэффициент Фехнера • Наиболее простым показателем, используемым для измерения тесноты зависимости при параллельном рассмотрении у n единиц значений x и y, является коэффициент Фехнера (коэффициент корреляции знаков).

Он основан на сравнении поведения отклонений индивидуальных значений каждого признака (x и y) от своей средней величины. При этом во внимание принимаются не величины отклонений (xi-xср) и (yi-yср), а их знаки ( «+» или «-» ). Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений и несовпадений

• Достоинство этого критерия связи состоит в том, что исходная информация может быть задана не численно, а словесно по принципу "больше" - "меньше". • Коэффициент КФ Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме.

если знаки всех отклонений по каждому признаку совпадают, то = 0 и тогда КФ = 1. Это характеризует наличие прямой связи. Если все знаки не совпадают, то = 0, КФ = -1, что характеризует обратную связь. Коэффициент Фехнера, как и любой другой показатель тесноты связи, может принимать значения от – 1 до +1. равенство КФ = 1 нельзя оценивать как свидетельство функциональной зависимости между x и y. Поскольку КФ зависит только от знаков и не учитывает величину самих отклонений x и y от их средних величин, то он практически характеризует не столько тесноту связи, сколько её наличие и направление.