Randomized Weighted Paging Online Algorithms meet Linear Programming

Randomized Weighted Paging (Online Algorithms meet Linear Programming) Nikhil Bansal IBM Research Niv Buchbinder Technion, Israel Seffi Naor Technion, Israel 1

Caching / Paging CPU cache Browser cache web 2

The Paging/Caching Problem Set of pages {1, 2, …, n}. Cache can hold k << n pages. Request sequence of pages 1, 6, 4, 1, 4, 7, 6, 1, 3, … a) If requested page already in cache, no penalty. b) Else, cache miss. Need to fetch page in cache (possibly) evicting some other page. Goal: Minimize the number of cache misses. Main Question: Upon a request, which page to evacuate? 3

Measuring Algorithm Quality Several natural page replacement algorithms: Least Recently used, Least Freq. Used, FIFO, … How to measure their performance? Statistical or Queueing Theoretic approach: Assume requests generated by some statistical process. Sampled from a probability distribution, Markov Chain, … Analyze an algorithm’s performance under this distribution. 4

Competitive Analysis No restriction on input sequence. Competitive ratio (Alg): max. I Alg(I) / OPT(I): The best possible offline solution for I Sleator Tarjan (1985) Example: Stock Market Make decisions based on current knowledge, But compare with best possible outcome in hindsight. Can we do anything at all. Surprisingly, Yes. 5

Example: Ski-Rental Problem: It costs $500 to buy skis, and $25 to rent. I don’t know how often I will ski. What strategy to use every time I go skiing? Answer: Rent first 19 times, then buy the 20 th time you go skiing. (20 = 500/25). Never worse than twice off. Competitive ratio = 2. (In worst case, go 20 times, pay both renting and buying costs) 6

Randomized Competitive Analysis Bad instance Game between adversary and algorithm Randomized Algorithm: Can toss coins and act accordingly Expected Competitive Ratio : max. I E[Alg(I)] / OPT(I) ? 7

Example: Ski-Rental Problem: It costs $500 to buy skis, and $25 to rent. I don’t know how often I will ski. What strategy to use every time I go skiing? Answer: pt: Probability of buying on day t. p 1 + p 2 + … + pt ¼ (et/b-1 ) / (e-1) Can achieve a ratio of e/(e-1) = 1. 58 (no matter what adversary does, our expected cost within 1. 58 times) 8

Outline 1) 2) 3) 4) 5) 6) Competitive Analysis Paging Problem: History Linear Programming Framework LP Duality and Proofs Weighted Paging Conclusions 9

Paging Problem Set of pages {1, 2, …, n}. Cache can hold k pages. Request sequence of pages 1, 6, 4, 1, 4, 7, 6, 1, 3, … a) If requested page already in cache, no penalty. b) Else, cache miss. Need to fetch page in cache (possibly) evicting some other page. Goal: Minimize cache misses. Historically, led to developments in competitive analysis. 10

Previous Results: Paging (Deterministic) [Sleator Tarjan 85]: • Any det. algorithm >= k-competitive. • LRU is k-competitive (also other algorithms) • LRU is k/(k-h+1)-competitive if optimal has cache of size h · k. Paging (Randomized): • Rand. Marking O(log k) • Lower bound Hk [Fiat, Karp, Luby, Mc. Geoch, Sleator, Young 91]. [Fiat et al. 91], tight results known. • O(log(k/k-h+1))-competitive algorithm if optimal has cache of size h · k [Young 91] 11

The Weighted Paging Problem One small change: • Each page i has a different fetching cost w(i). • Models scenarios where cost of bringing pages is not uniform: Main memory, disk, internet … web Goal • Minimize the total cost of cache misses. 12

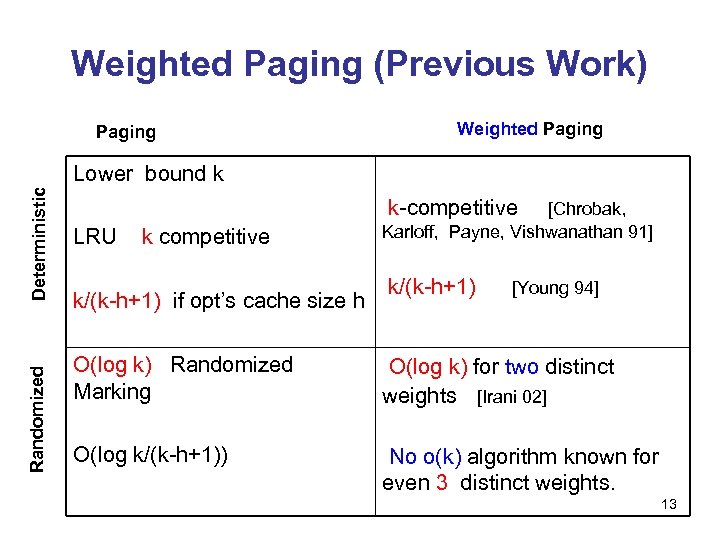Weighted Paging (Previous Work) Paging Weighted Paging Randomized Deterministic Lower bound k k-competitive LRU k competitive k/(k-h+1) if opt’s cache size h [Chrobak, Karloff, Payne, Vishwanathan 91] k/(k-h+1) [Young 94] O(log k) Randomized Marking O(log k) for two distinct weights [Irani 02] O(log k/(k-h+1)) No o(k) algorithm known for even 3 distinct weights. 13

The k-server Problem • k servers lie in an n-point metric space. • Requests arrive at points. • To serve request: Must move some server there. Goal: Minimize total distance traveled. • Paging = k-server on a uniform metric. (every page is a point, page in cache iff server on the point) • Weighted paging = k-server on a weighted star metric. Lower Bound: (log k) (widely believed right answer) No < k competitive algorithms known, even for very simple spaces. 14

Our Results Weighted Paging (Randomized): • O(log k)-competitive algorithm for weighted paging. • O(log (k/k-h+1))-competitive if opt’s cache size h

Outline 1) 2) 3) 4) 5) 6) Competitive Analysis Paging Problem: History Linear Programming Framework LP Duality and Proofs Weighted Paging Conclusions 16

Linear Programming Linear constraints, linear objective Min x 1 – 3 x 2 + 2 x 3 x 1 – x 2 + 7 x 3 <= 2 x 2 - x 3 >= 0 x 1 + 3 x 2 + x 3 >= -3 Polynomial time solvable. Lies at the heart of optimization. 17

An Abstract Online Problem min 3 x 1 + 5 x 2 + x 3 + 4 x 4 + … 2 x 1 + x 3 + x 6 + … ¸ 3 x 3 + x 14 + x 19 + … ¸ 8 x 2 + 7 x 4 + x 12 + … ¸ 2 Covering LP (non-negative entries) Goal: Find feasible solution x* with min cost. Requirements: 1) Upon arrival constraint must be satisfied 2) Cannot decrease a variable (online nature) 18

Example min x 1 + x 2 + … + xn x 1 + x 2 + x 3 + … + xn ¸ 1 Set all xi to 1/n Increase x 2 , x 3, …, xn to 1/n-1 … … xn ¸ 1 Online ¸ ln n Increase xn to 1 (1+1/2+ 1/3+ … + 1/n) Opt = 1 ( xn=1 suffices) 19

Powerful Abstraction The online covering LP problem (and its dual packing counterpart) is a powerful framework Ski-Rental, Adword auctions, Dynamic TCP acknowledgement, Online Routing, Load Balancing, Congestion Minimization, Caching, Online Matching, Online Graph Covering, Parking Permit Problem, … Unified Framework for various previously studied problems. Exposes underlying structure / gives improved guarantees for many problems. But let first see how to model problems. 20

Ski Rental – Integer Program Subject to: For each day i: (either buy or rent) 21

General Covering/Packing Results For a {0, 1} covering/packing matrix: [Buchbinder Naor 05] – Competitive ratio O(log D) – Can get e/e-1 for ski rental and other problems. (D – max number of non-zero entries in a constraint). Remarks: • • • Fractional solutions Number of constraints/variables can be exponential. There can be a tradeoff between the competitive ratio and the factor by which constraints are violated. Fractional solution ! randomized algorithm (online rounding) 22

General Covering/Packing Results For a general covering/packing matrix [BN 05] : Covering: – Competitive ratio O(log n) (n – number of variables). Packing: – Competitive ratio O(log n + log [a(max)/a(min)]) a(max), a(min) – max/min non-zero entry Remarks: • • Results are tight. Can add “box” constraints to covering LP (e. g. x · 1) 23

Outline 1) 2) 3) 4) 5) 6) Competitive Analysis Paging Problem: History Linear Programming Framework LP Duality and Proofs Weighted Paging Conclusions 24

Duality Min 3 x 1 + 4 x 2 x 1 + x 2 >= 3 x 1 + 2 x 2 >= 5 Want to convince someone that there is a solution of value 12. Easy, just demonstrate a solution, x 2 = 3 25

Duality Min 3 x 1 + 4 x 2 x 1 + x 2 >= 3 x 1 + 2 x 2 >= 5 Want to convince someone that there is no solution of value 10. How? 2 * first eqn + second eqn 3 x 1 + 4 x 2 >= 11 LP Duality Theorem: This seemingly ad hoc trick always works! 26

LP Duality Min cj xj j aij xj ¸ bi Linear combination (y ¸ 0) i yi j aij xj ¸ i yi bi j xj ( i aij yi ) ¸ i yi bi So, for any y ¸ 0 satisfying i aij yi · cj for all i j xj cj ¸ i yi bi Dual LP Dual cost Equality when Complementary Slackness i. e. yi > 0 (only if corresponding primal constraint is tight) xi > 0 (only if corresponding dual constraint is tight) 27

Generic Primal-Dual Approach min cx Ax ¸ b x¸ 0 (primal) max b y At y · c y¸ 0 (dual) Generic Primal Dual Algorithm: 0) Start with x=0, y=0 (primal infeasible, dual feasible) 1) Increase dual and primal together, s. t. if dual cost increases by 1, primal increases by · c 2) If both dual and primal feasible ) c approximate solution 28

Key Idea for Online Primal Dual Primal: Min i ci xi Dual Step t, new constraint: a 1 x 1 + a 2 x 2 + … + ajxj ¸ bt New variable yt + bt yt in dual objective How much: xi ? yt ! yt + 1 (additive update) primal cost = = Dual Cost dx/dy proportional to x so, x varies as exp(y) 29

How to initialize A problem: dx/dy is proportional to x, but x=0 initially. So, x will remain equal to 0 ? Answer: Initialize to 1/n. When: Complementary slackness tells us that x > 0 only if dual constraint corresponding to x is tight. Set x=1/n when its dual constraint becomes tight. 30

The Algorithm Min j cj xj j aij xj ¸ bi On arrival of i-th constraint, Initialize yi=0 (dual var. for constraint) If current constraint unsatisfied, gradually increase yi If xj =0, set xj = 1/n when i aij yi = cj (dual tight) else update xj exponentially as 1/n ¢ exp( ( i aij yi / cj) - 1 ) Proof: 1) Primal Cost · Dual Cost 2) Dual solution violated by O(log n) factor. 31

Outline 1) 2) 3) 4) 5) 6) Competitive Analysis Paging Problem: History Linear Programming Framework LP Duality and Proofs Weighted Paging Conclusions 32

Fractional Weighted Paging Model: • Fractions of pages are kept in cache: probability distribution over pages p 1, …, pn • The total sum of fractions of pages in the cache is at most k. • If pi changes by , cost = w(i) k units of cache 33

Weight Paging – Linear Program (i, 2) (i, 1) Pg i’ Pg i Time line Pg i’ t Pg i’ Pg i If interval present, no cache miss. At any time step t, can have at most k such intervals. Equivalently, at least n-k intervals must be absent B(t): number of distinct pages requested by time t x(i, j): How much interval (i, j) evacuated thus far 0 · x(i, j) · 1 Cost = i w(i) j x(i, j) i : i pt x(i, r(i, t)) ¸ n-k 8 t 34

Direct application of Primal-Dual Framework gives O(log n) competitive ratio. Specialized tricks to obtain an O(log k) ratio (details omitted) Thm: This gives the fractional O(log k) competitive algorithm for weighted paging. 35

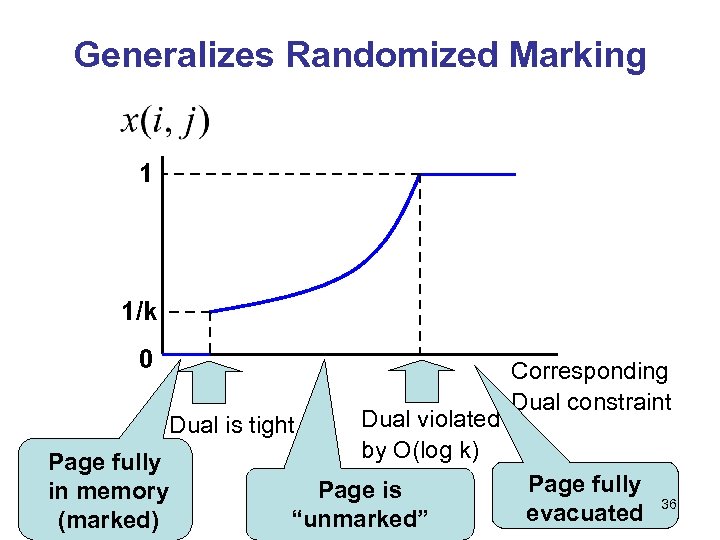Generalizes Randomized Marking 1 1/k 0 Dual is tight Page fully in memory (marked) Dual violated by O(log k) Page is “unmarked” Corresponding Dual constraint Page fully evacuated 36

Need for careful rounding K=2, Pages A, B, C, D LP state: (1/2, 1/2) New LP state: (1, 0, 1/2) Only consistent cache state: A, B have wt. 1, Cache state: C, D have wt. M ½ (A, B) + ½ (C, D) ½ (A, C) + ½ (A, D) (need to move C or D, incur cost >> than LP cost) Thm: Can maintain state s. t. only incur O(1) times LP cost. Together with fractional O(log k) result, implies an O(log k) competitive algorithm for weighted paging. 37

Concluding Remarks Primal-dual gives simple unifying framework for caching. (LP needed only for analysis, algorithm much simpler) Can also give O(log 2 k) compet. algorithm for general caching. (Pages have both arbitrary sizes and weights) Extend (partially) beyond covering/ packing problems. Apply to online learning with experts. Future Directions: 1. O(log k) algorithms for k-server. (or even < k for a start ? ) 2. Unified theory connecting online learning/prediction and competitive analysis. 38

Thank you 39