c864d5f95863f4e6713691eba8794cbd.ppt
- Количество слайдов: 54

Raising Revenue With Raffles: Evidence from a Laboratory Experiment Wooyoung Lim, University of Pittsburgh Alexander Matros, University of Pittsburgh Theodore Turocy, Texas A&M University 1

Lotteries n As of 2008, 43 States have State Lotteries n 33% - 50% of USA population participates 2

Lotteries A lottery is a salutary instrument and a tax. . . laid on the willing only, that is to say, on those who can risk the price of a ticket without sensible injury, for the possibility of a higher prize. Thomas Jefferson 3

Lotteries Too many players buy too many tickets Why? 4

Literature (A) Buy Hope? Clotfelter and Cook (1989, 1990, 1993) n 5

Literature (A) Buy Hope? Clotfelter and Cook (1989, 1990, 1993) n (B) Charity/Fund raising? Morgan (2000), Morgan and Sefton (2000) n 6

Literature (A) Buy Hope? Clotfelter and Cook (1989, 1990, 1993) n (B) Charity/Fund raising? Morgan (2000), Morgan and Sefton (2000) n n What if no (A) and no (B)? 7

Plan n n n Theory Experiments Data Behavioral Models Results Conclusion 8

Theory n risk neutral players V – prize value W – endowment xi 0 player i’s expenditure 9

Players’ maximization problem Player i solves the following problem 10

Rationalizable choices 11
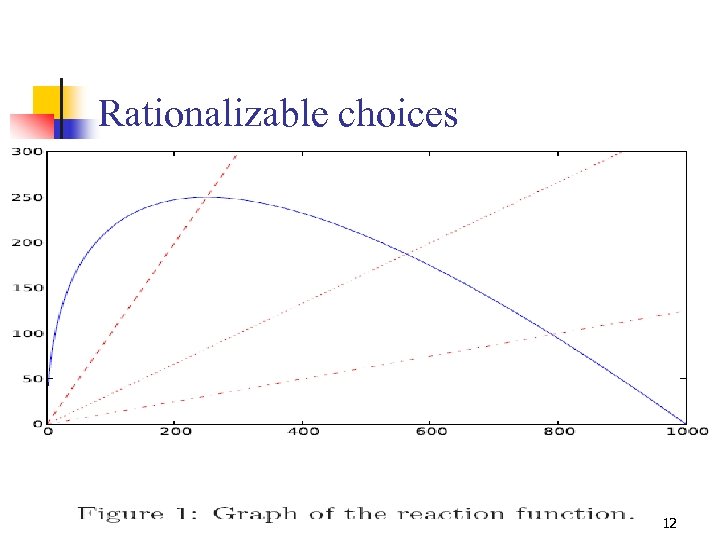
Rationalizable choices 12
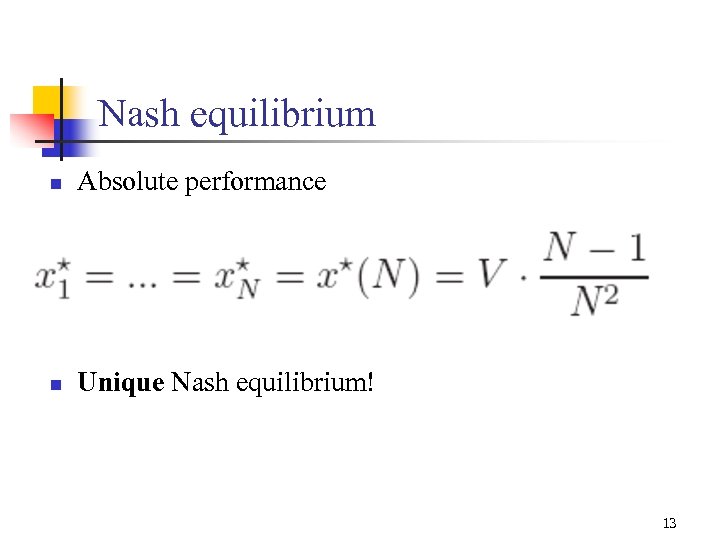
Nash equilibrium n Absolute performance n Unique Nash equilibrium! 13

Evolutionary Stable Strategies n Relative performance (spiteful behavior) 14
Experimental Design V = 1, 000 tokens (= $10) W = 1, 200 tokens (= $12) Quizzes Expected payoff tables N = 2, 3, 4, 5, 9 3 sessions for each N Pittsburgh Experimental Economics Laboratory October 2007 – March 2008 15

Experimental Design Quiz 1 Assume that your contribution is 100 tokens and your opponent’s contribution is 900 tokens. What is your chance to win the lottery? n n n 100 / 900 100 / 1, 000 100 / 800 / 900 / 1, 000 Assume that your contribution is 900 tokens and your opponent’s contribution is 100 tokens. What is your chance to win the lottery? n n n 100 / 900 100 / 1, 000 800 / 900 / 1, 000 900 / 900 16

Experimental Design Quiz 2 Assume that your contribution is 100 tokens and your opponent’s contribution is 900 tokens. What is your expected payoff? n n n -100 0 100 900 1, 000 Assume that your contribution is 900 tokens and your opponent’s contribution is 100 tokens. What is your expected payoff? n n n - 900 - 100 0 100 900 17
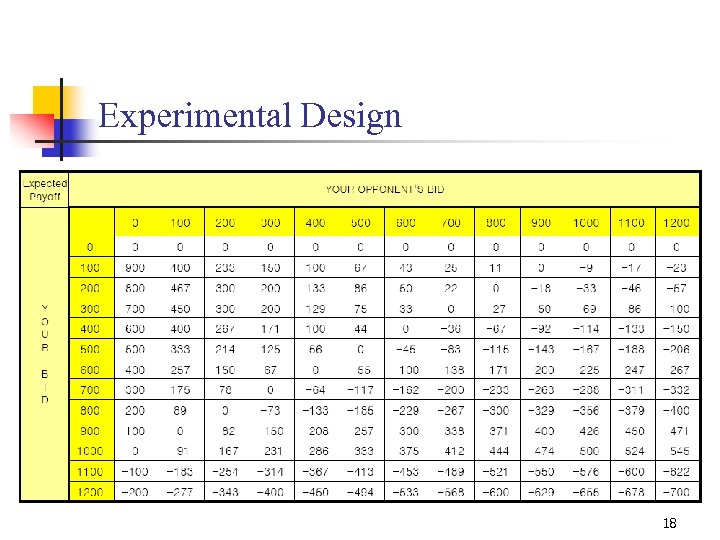
Experimental Design 18
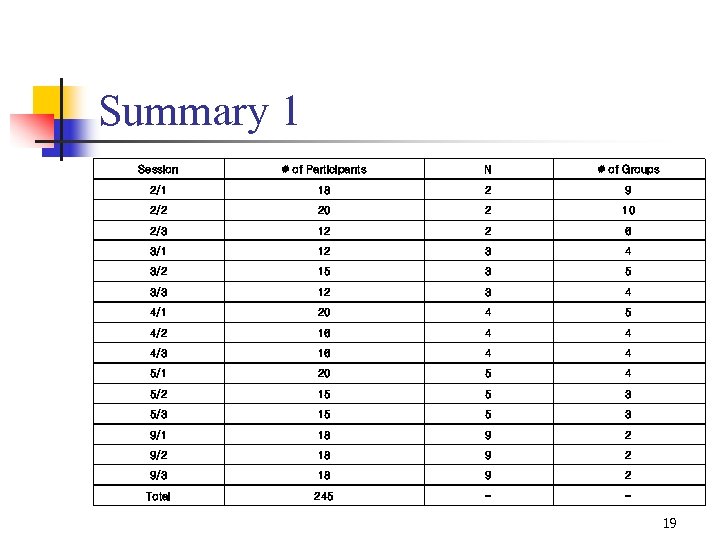
Summary 1 Session # of Participants N # of Groups 2/1 18 2 9 2/2 20 2 10 2/3 12 2 6 3/1 12 3 4 3/2 15 3 5 3/3 12 3 4 4/1 20 4 5 4/2 16 4 4 4/3 16 4 4 5/1 20 5 4 5/2 15 5 3 5/3 15 5 3 9/1 18 9 2 9/2 18 9 2 9/3 18 9 2 Total 245 - - 19
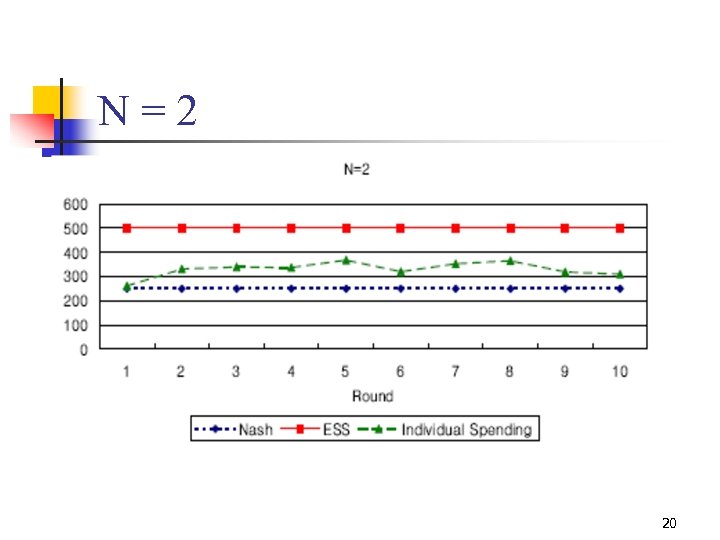
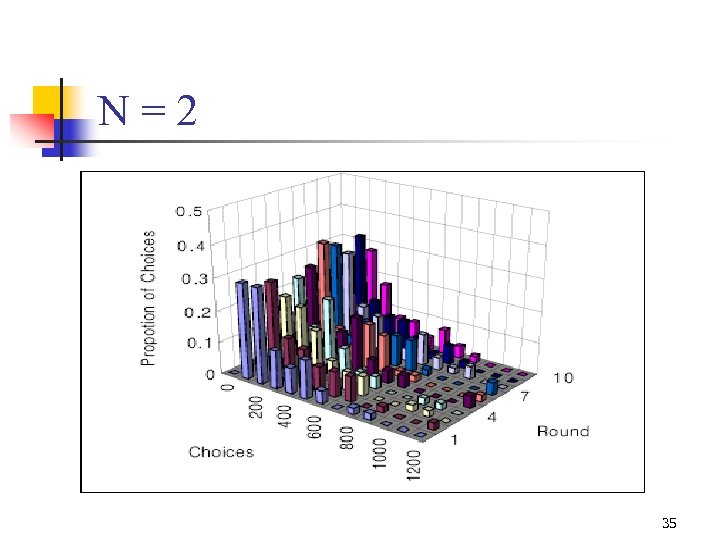
N=2 20
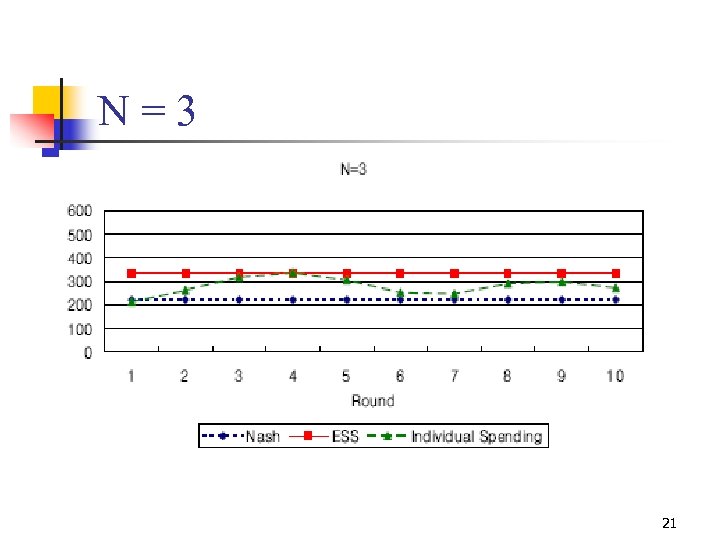
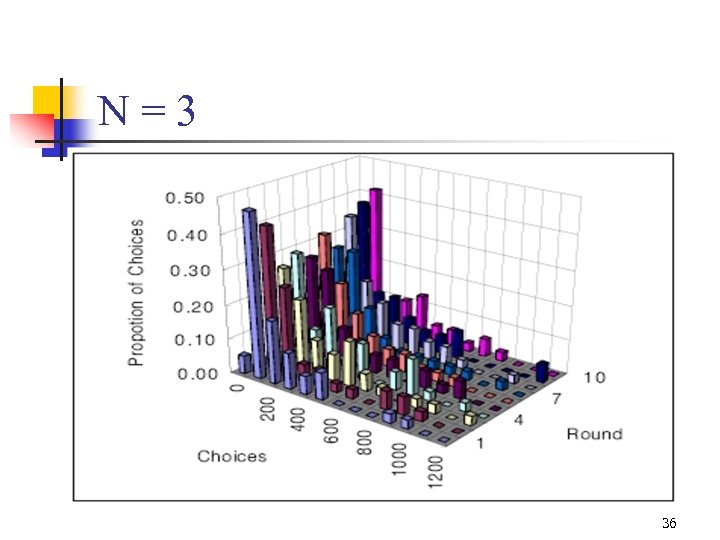
N=3 21
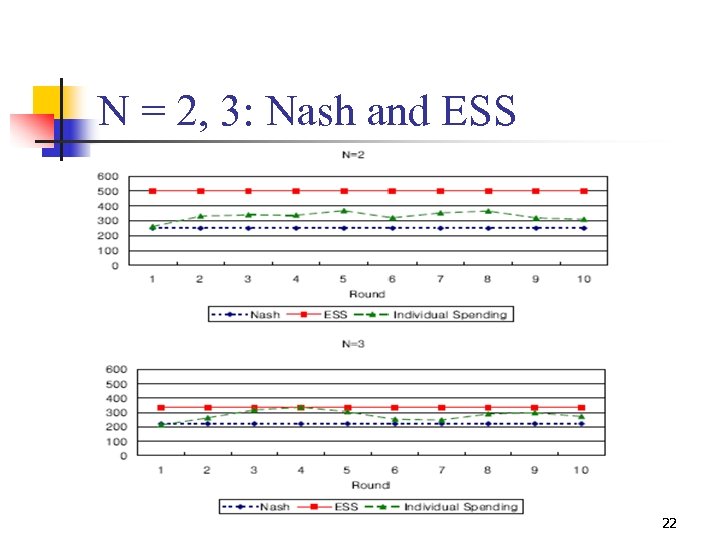
N = 2, 3: Nash and ESS 22
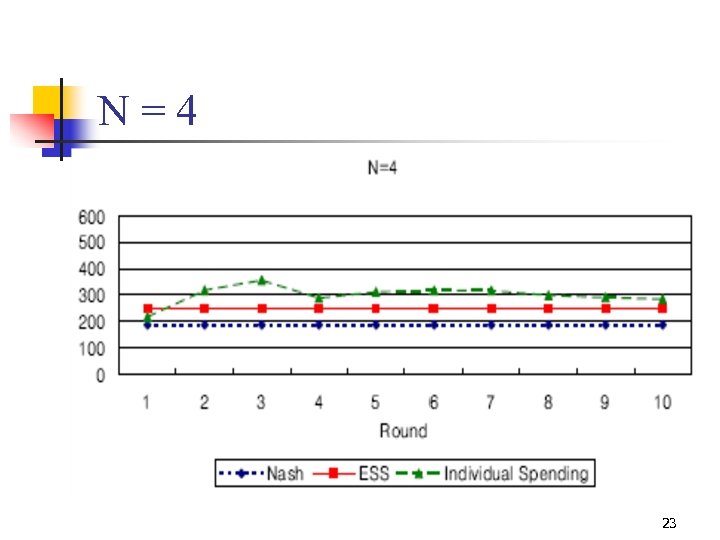
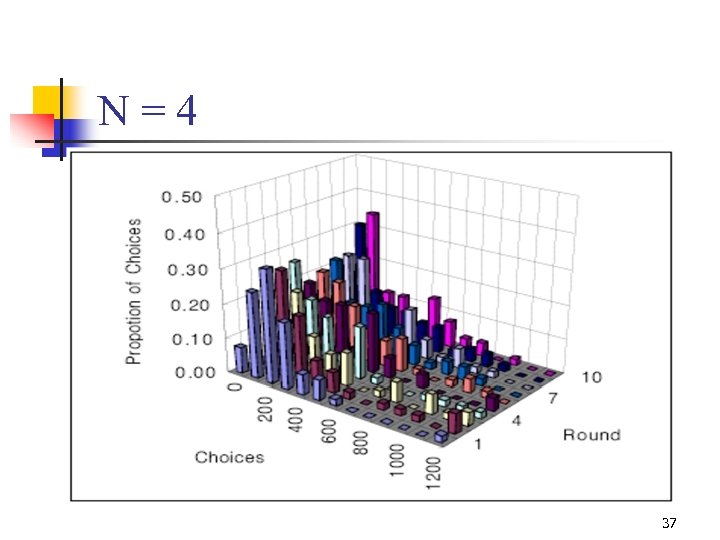
N=4 23
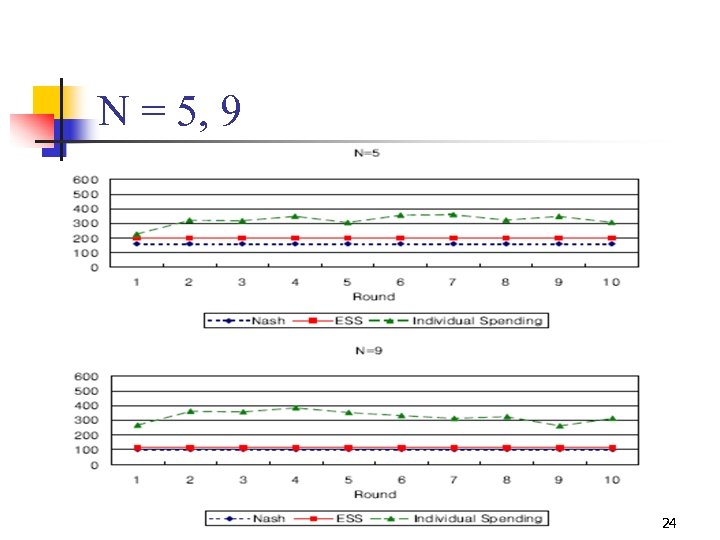
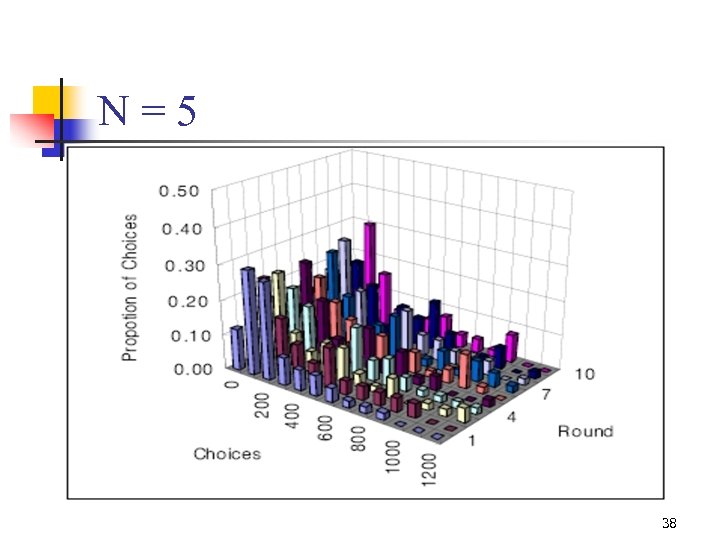
N = 5, 9 24
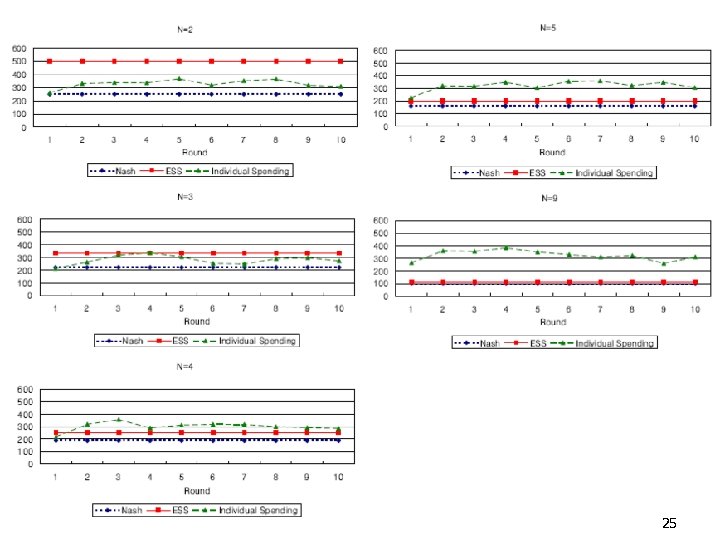
25
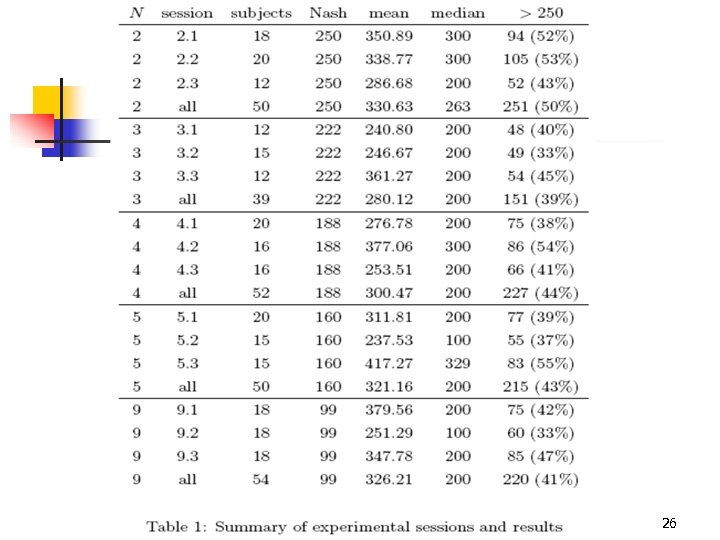
26
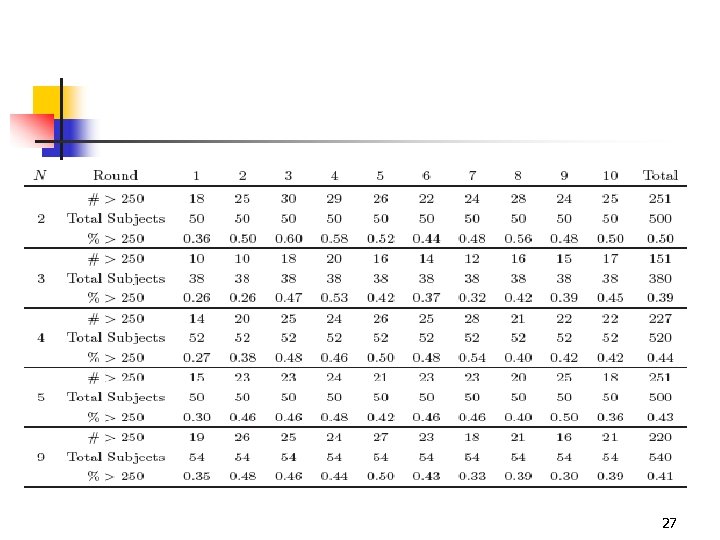
27

Data n n Integer multiples of 100 in 78. 1% Integer multiples of 50 in 87. 7% (+9. 6%) 28
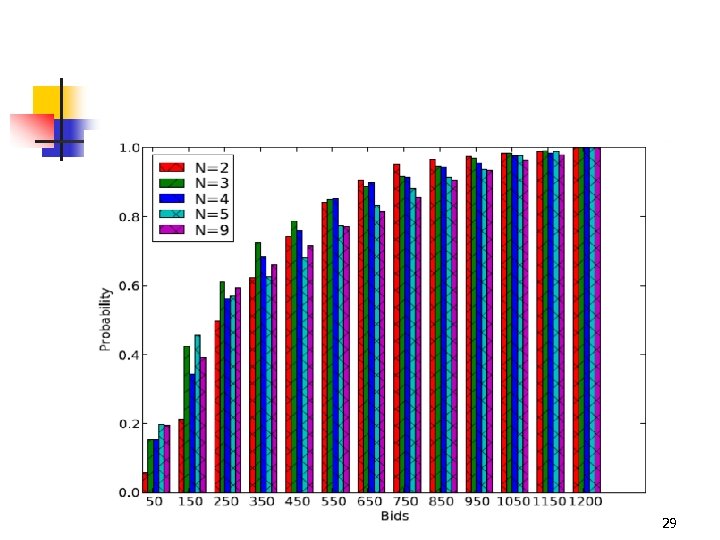
29

Behavioral Predictions n n n Quantal Response Equilibrium Level – k reasoning Learning Direction Theory 30

Quantal Response Equilibrium n n n Mc. Kelvey and Palfrey (1995) Noisy optimization process - the best parameter (from the data) = 0 – all choices are random = – no noise (QRE Nash) 31
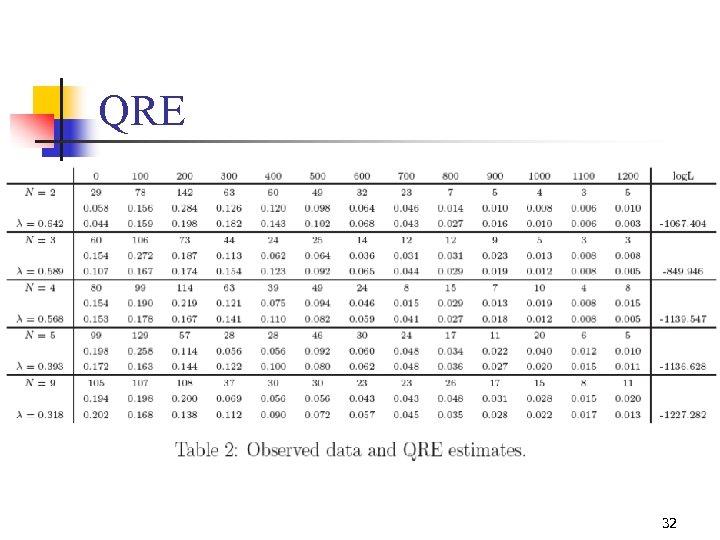
QRE 32
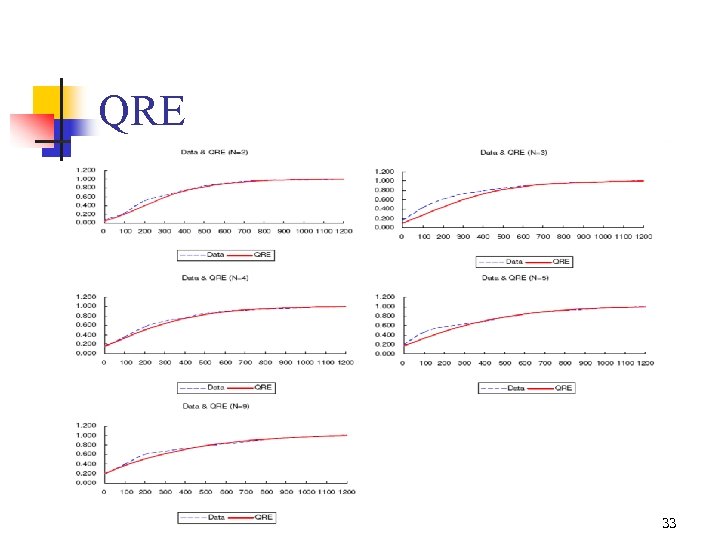
QRE 33

Level – k reasoning n n Stahl and Wilson (1994, 1995) Level – 0: random Level – 1: best reply to Level – 0 Level – 2: best reply to Level – 1 34
N=2 35
N=3 36
N=4 37
N=5 38
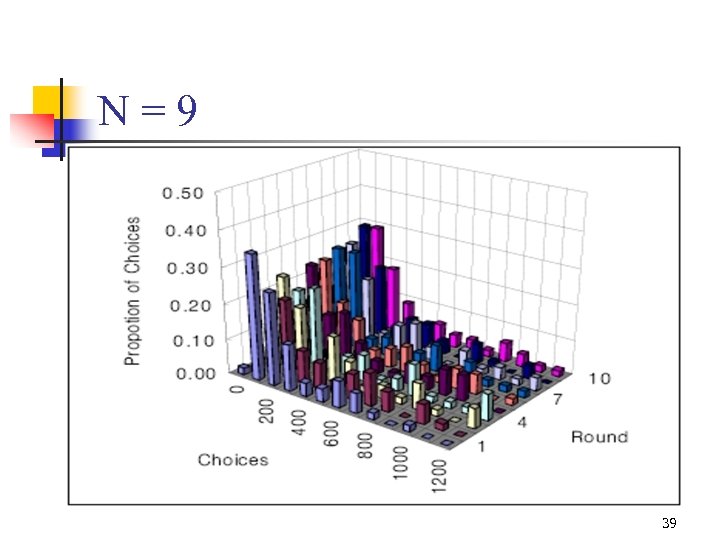
N=9 39

Level – k reasoning n n Ho, Camerer and Weigelt (1998) Level – 0: uniform on [0, V] – density B 0 Level – 1: simulate N-1 draws from B 0 compute best reply Level – 2: 40
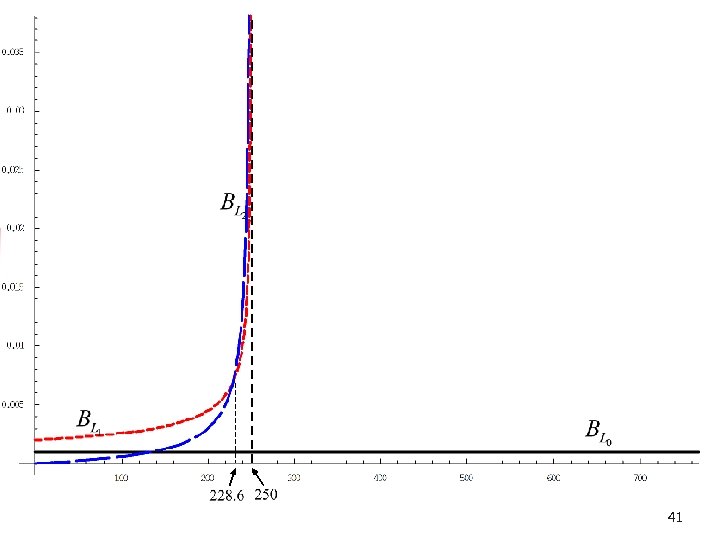
41
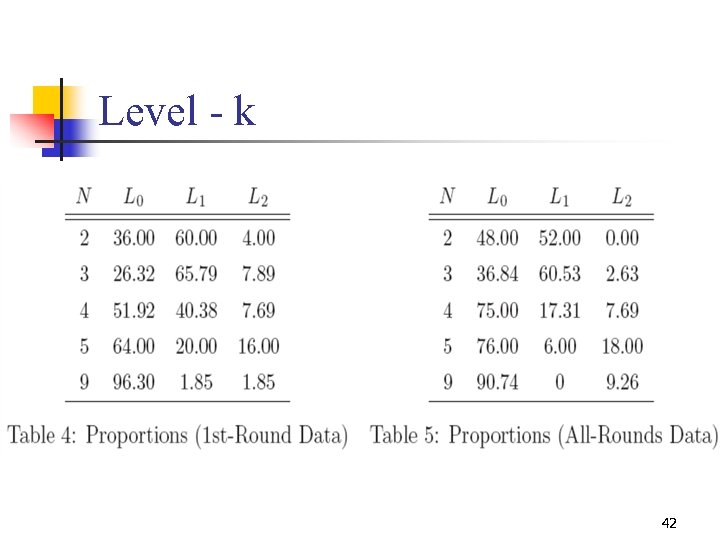
Level - k 42

Level – k reasoning n n Level – 0 in N Level – 1 in N Costa-Gomes and Crawford (2004) classify subjects: at least 6 out of 10 96% can be classified! Iterated elimination of dominated strategies: No 43

Learning Direction Theory n n Selten and Buchta (1994) “Subjects are more likely to change their past actions in the directions of a best response to the others’ previous period actions. ” 44
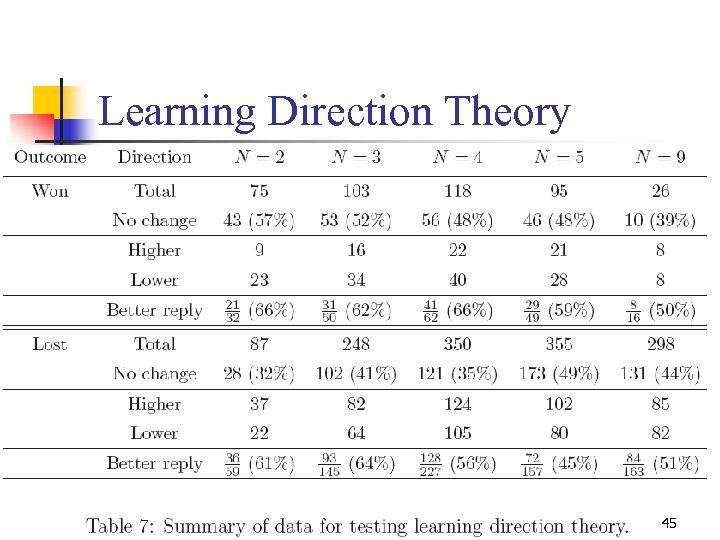
Learning Direction Theory 45

Learning Direction Theory If you lose, you change “Small lotteries” Yes Other lotteries No n If you win: you overpaid; if you lose: you underpaid “Small lotteries” Yes Other lotteries No n Adjust in the best reply direction “Small lotteries” Yes Other lotteries No n 46

Conclusion Subjects’ behavior in lotteries w/t (A) and (B) a) Nash equilibrium b) ESS c) QRE d) Level – k reasoning e) Leaning direction theory 47

Conclusion Data a) “Almost” do not change to change in N b) Overspending even for N = 4, 5, 9 48

Conclusion Data: N = 2 a) Nash c) QRE d) Level – k reasoning e) Leaning direction theory (the least noise) (Level – 1) (BR changes) 49

Conclusion Data: N = 3 b) SSE c) QRE d) Level – k reasoning e) Leaning direction theory (noise) (Level – 1) (some BR changes) 50

Conclusion Data: N = 4, 5, 9 c) QRE d) Level – k reasoning e) Leaning direction theory (noise) (Level – 0) (random changes) 51
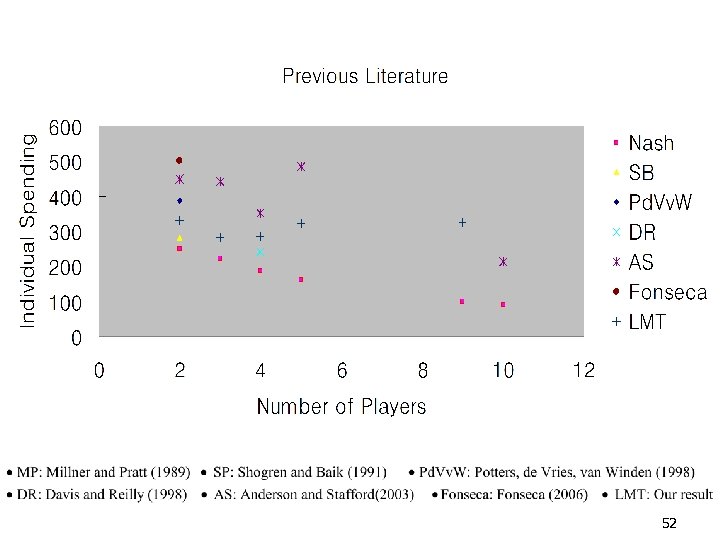
52
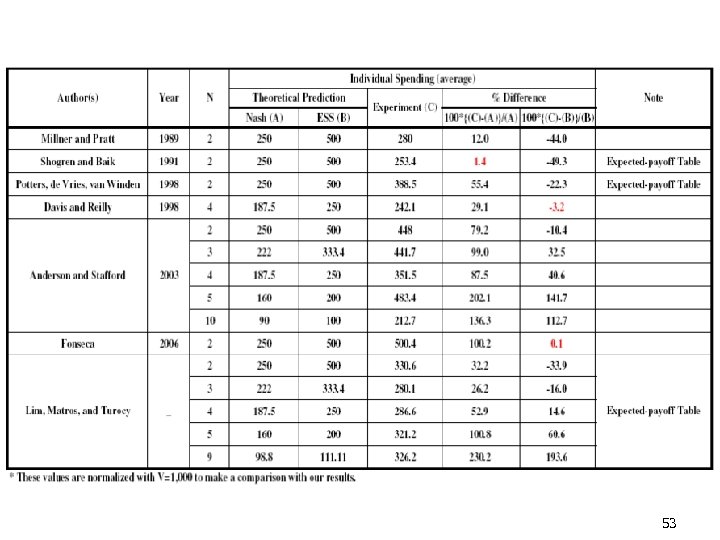
53

Conclusion Lotteries: N > 4 n n n Boundedly rational subjects “Random” choices Overspending! 54
c864d5f95863f4e6713691eba8794cbd.ppt