Электрические фильтры.pptx
- Количество слайдов: 63
 РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ Электрические фильтры
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ Электрические фильтры
 РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. С. И. Баскаков «Радиотехнические цепи и сигналы» , 2003 г. 2. С. И. Баскаков «Радиотехнические цепи и сигналы. Руководство к решению задач» , 2002 г. 4. В. И. Нефёдов «Основы радиоэлектроники и связи» , 2002 г. 5. М. Т. Иванов, А. Б. Сергиенко, В. Н. Ушаков, «Теоретические основы радиотехники» , 2002 г. 6. В. И. Нефёдов «Основы радиоэлектроники и связи» , 2009 г.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. С. И. Баскаков «Радиотехнические цепи и сигналы» , 2003 г. 2. С. И. Баскаков «Радиотехнические цепи и сигналы. Руководство к решению задач» , 2002 г. 4. В. И. Нефёдов «Основы радиоэлектроники и связи» , 2002 г. 5. М. Т. Иванов, А. Б. Сергиенко, В. Н. Ушаков, «Теоретические основы радиотехники» , 2002 г. 6. В. И. Нефёдов «Основы радиоэлектроники и связи» , 2009 г.
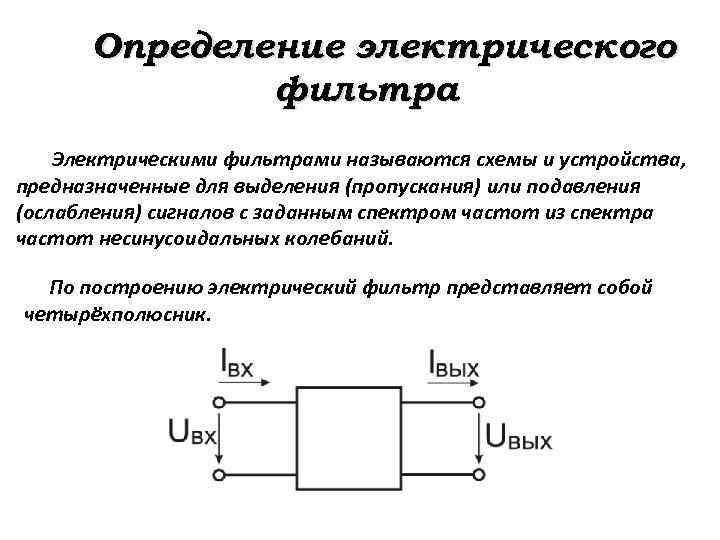 Определение электрического фильтра Электрическими фильтрами называются схемы и устройства, предназначенные для выделения (пропускания) или подавления (ослабления) сигналов с заданным спектром частот из спектра частот несинусоидальных колебаний. По построению электрический фильтр представляет собой четырёхполюсник.
Определение электрического фильтра Электрическими фильтрами называются схемы и устройства, предназначенные для выделения (пропускания) или подавления (ослабления) сигналов с заданным спектром частот из спектра частот несинусоидальных колебаний. По построению электрический фильтр представляет собой четырёхполюсник.
 Полоса прозрачности и полоса задерживания
Полоса прозрачности и полоса задерживания
 Классификация электрических фильтров В соответствии с взаимным расположением областей прозрачности и задерживания на шкале частот различают следующие виды фильтров:
Классификация электрических фильтров В соответствии с взаимным расположением областей прозрачности и задерживания на шкале частот различают следующие виды фильтров:
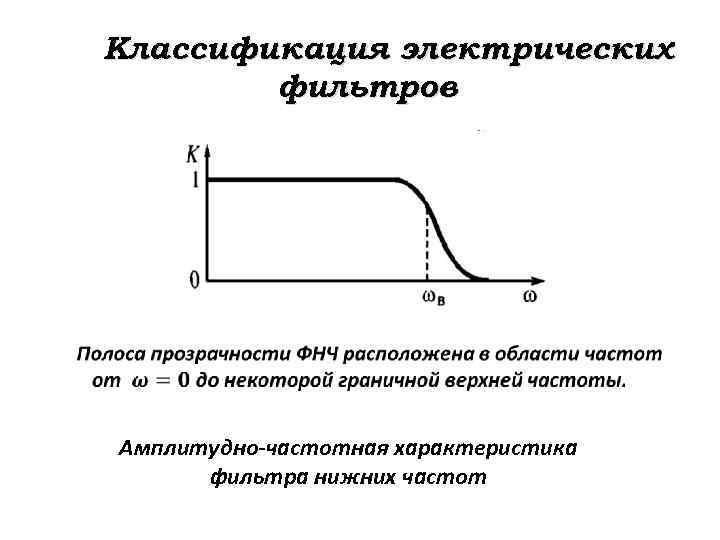 Классификация электрических фильтров Амплитудно-частотная характеристика фильтра нижних частот
Классификация электрических фильтров Амплитудно-частотная характеристика фильтра нижних частот
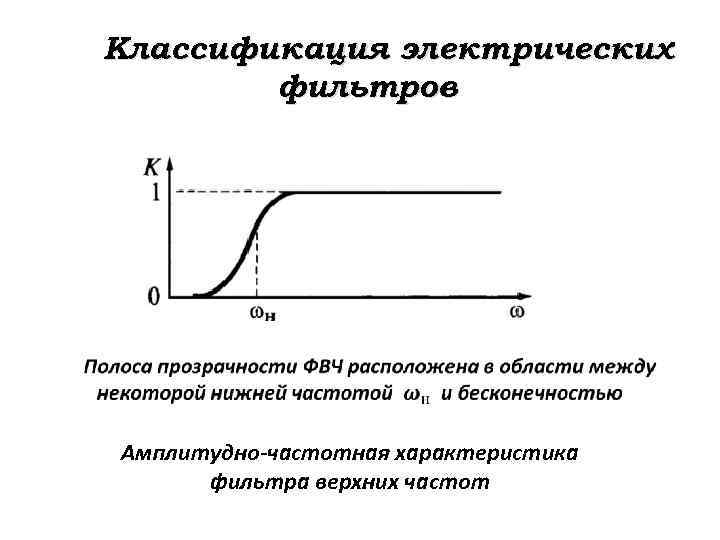 Классификация электрических фильтров Амплитудно-частотная характеристика фильтра верхних частот
Классификация электрических фильтров Амплитудно-частотная характеристика фильтра верхних частот
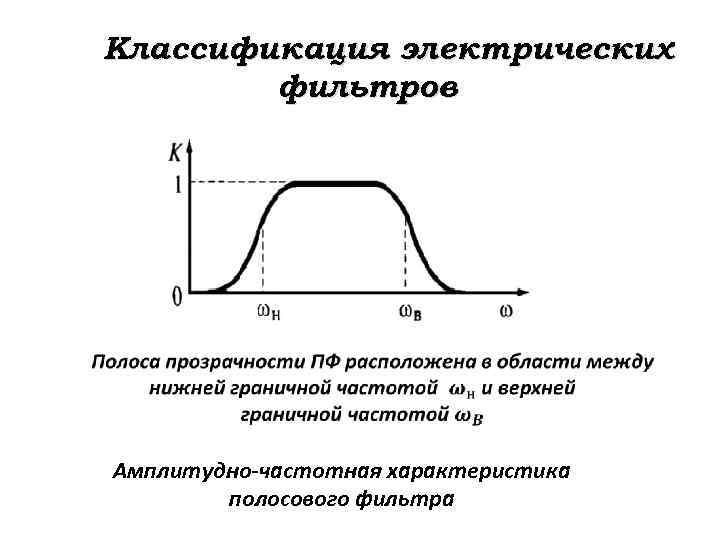 Классификация электрических фильтров Амплитудно-частотная характеристика полосового фильтра
Классификация электрических фильтров Амплитудно-частотная характеристика полосового фильтра
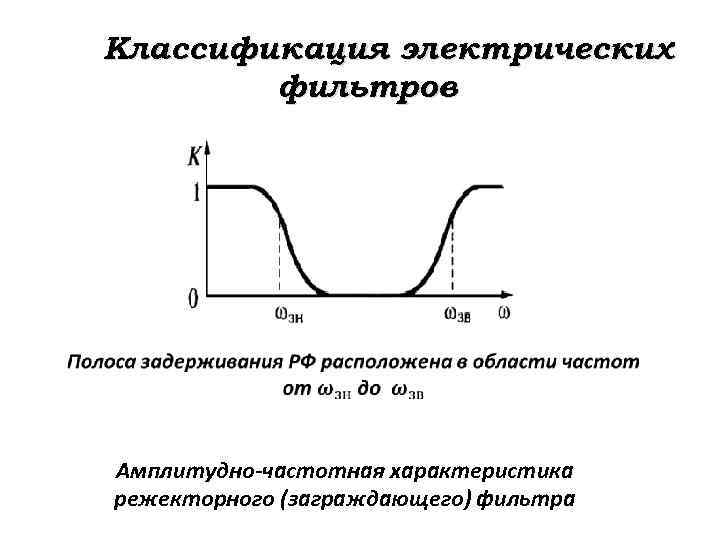 Классификация электрических фильтров Амплитудно-частотная характеристика режекторного (заграждающего) фильтра
Классификация электрических фильтров Амплитудно-частотная характеристика режекторного (заграждающего) фильтра
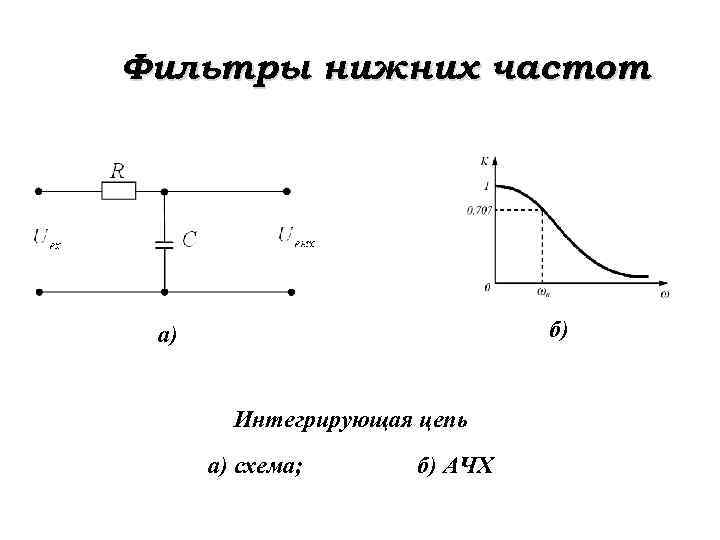 Фильтры нижних частот б) а) Интегрирующая цепь а) схема; б) АЧХ
Фильтры нижних частот б) а) Интегрирующая цепь а) схема; б) АЧХ
 Частотный коэффициент передачи по мощности частотная характеристика) ( Частотный коэффициент передачи по мощности идеального ФНЧ для физических (положительных) частот описывается следующим аналитическим выражением: . . . (1) В теории электрических фильтров идеальные частотные характеристики аппроксимируют различными функциональными зависимостями.
Частотный коэффициент передачи по мощности частотная характеристика) ( Частотный коэффициент передачи по мощности идеального ФНЧ для физических (положительных) частот описывается следующим аналитическим выражением: . . . (1) В теории электрических фильтров идеальные частотные характеристики аппроксимируют различными функциональными зависимостями.
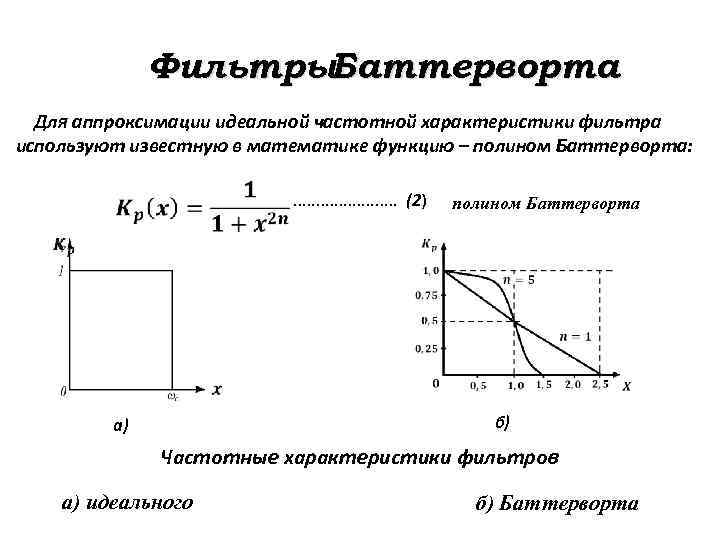 Фильтры. Баттерворта Для аппроксимации идеальной частотной характеристики фильтра используют известную в математике функцию – полином Баттерворта: . . . (2) полином Баттерворта б) а) Частотные характеристики фильтров а) идеального б) Баттерворта
Фильтры. Баттерворта Для аппроксимации идеальной частотной характеристики фильтра используют известную в математике функцию – полином Баттерворта: . . . (2) полином Баттерворта б) а) Частотные характеристики фильтров а) идеального б) Баттерворта
 Фильтры. Баттерворта Фильтры, построенные на основе этой функции, называются фильтрами с максимально плоскими характеристиками, или фильтрами Баттерворта. Целое число n = 1, 2, 3, . . . в формуле (2) определяет порядок (в данном случае – порядок полинома) фильтра.
Фильтры. Баттерворта Фильтры, построенные на основе этой функции, называются фильтрами с максимально плоскими характеристиками, или фильтрами Баттерворта. Целое число n = 1, 2, 3, . . . в формуле (2) определяет порядок (в данном случае – порядок полинома) фильтра.
 Фильтры. Баттерворта Ослабление оценивают в точках характеристики, где частота превышает частоту среза вдвое (на октаву) и в десять раз (на декаду). При этом ослабление (д. Б):
Фильтры. Баттерворта Ослабление оценивают в точках характеристики, где частота превышает частоту среза вдвое (на октаву) и в десять раз (на декаду). При этом ослабление (д. Б):
 Фильтры. Баттерворта
Фильтры. Баттерворта
 Фильтры. Чебышёва . . (3) В этом случае частотная характеристика ФНЧ имеет вид: . . . . (4)
Фильтры. Чебышёва . . (3) В этом случае частотная характеристика ФНЧ имеет вид: . . . . (4)
 Фильтры. Чебышёва
Фильтры. Чебышёва
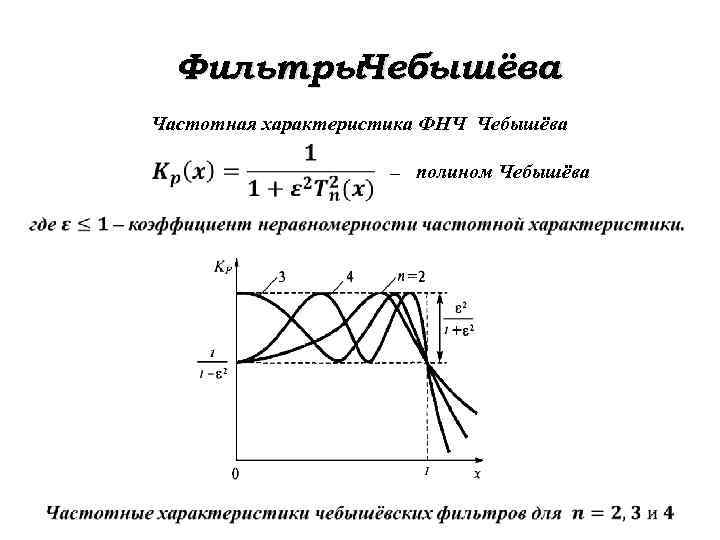 Фильтры. Чебышёва Частотная характеристика ФНЧ Чебышёва – полином Чебышёва
Фильтры. Чебышёва Частотная характеристика ФНЧ Чебышёва – полином Чебышёва
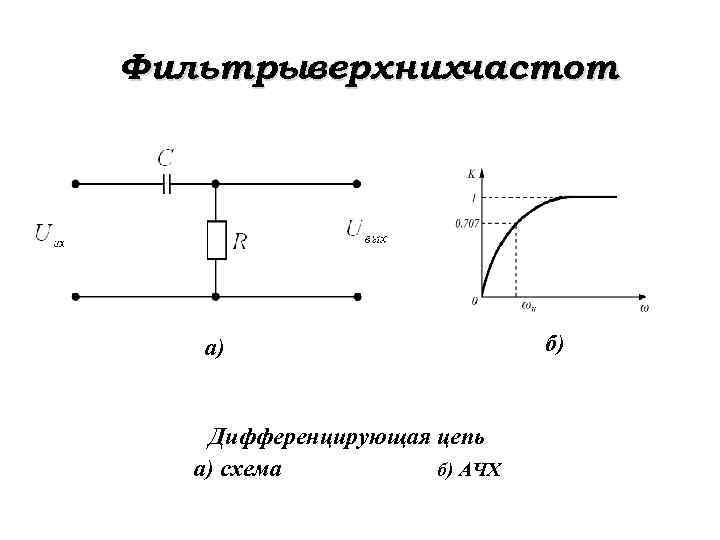 Фильтрыверхнихчастот а) Дифференцирующая цепь а) схема б) АЧХ б)
Фильтрыверхнихчастот а) Дифференцирующая цепь а) схема б) АЧХ б)
 Фильтры верхних частот Аппроксимацию идеальной частотной характеристики ФВЧ можно получить на основе полиномов Баттерворта и Чебышёва. Введём новую нормированную частоту Тогда . . . (5) . . . (6)
Фильтры верхних частот Аппроксимацию идеальной частотной характеристики ФВЧ можно получить на основе полиномов Баттерворта и Чебышёва. Введём новую нормированную частоту Тогда . . . (5) . . . (6)
 Фильтры верхних частот
Фильтры верхних частот
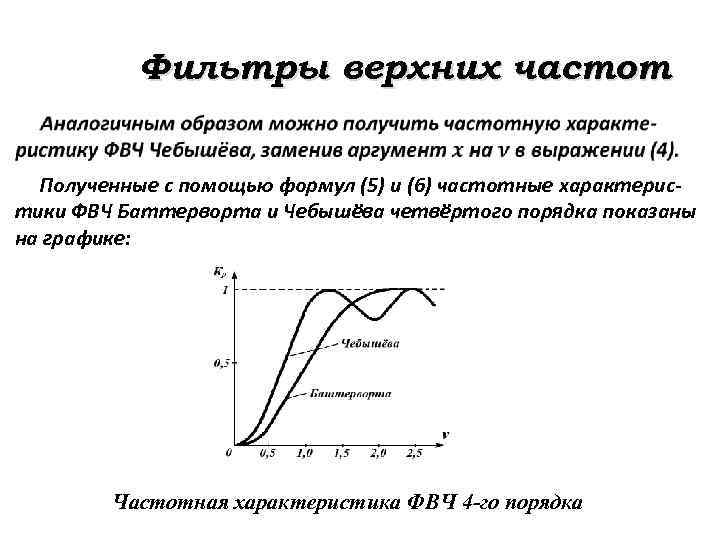 Фильтры верхних частот Полученные с помощью формул (5) и (6) частотные характеристики ФВЧ Баттерворта и Чебышёва четвёртого порядка показаны на графике: Частотная характеристика ФВЧ 4 -го порядка
Фильтры верхних частот Полученные с помощью формул (5) и (6) частотные характеристики ФВЧ Баттерворта и Чебышёва четвёртого порядка показаны на графике: Частотная характеристика ФВЧ 4 -го порядка
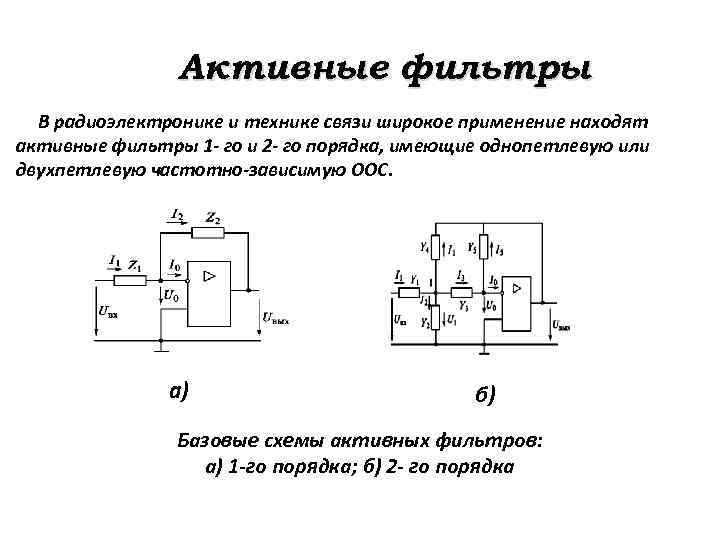 Активные фильтры В радиоэлектронике и технике связи широкое применение находят активные фильтры 1 - го и 2 - го порядка, имеющие однопетлевую или двухпетлевую частотно-зависимую ООС. а) б) Базовые схемы активных фильтров: а) 1 -го порядка; б) 2 - го порядка
Активные фильтры В радиоэлектронике и технике связи широкое применение находят активные фильтры 1 - го и 2 - го порядка, имеющие однопетлевую или двухпетлевую частотно-зависимую ООС. а) б) Базовые схемы активных фильтров: а) 1 -го порядка; б) 2 - го порядка
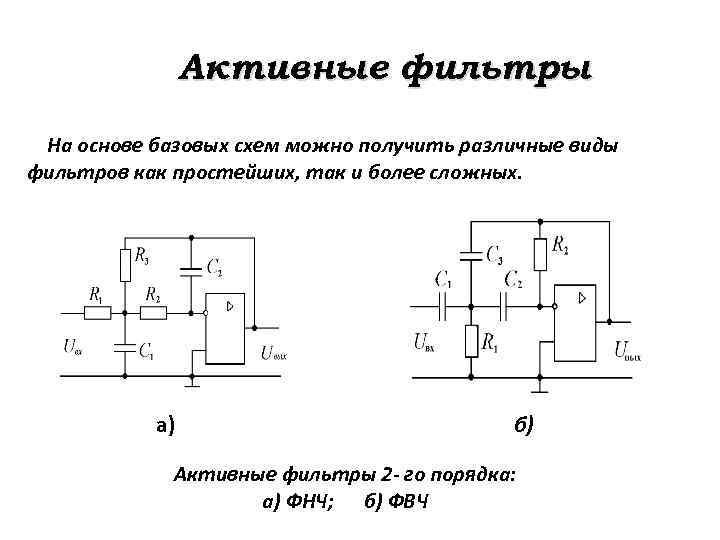 Активные фильтры На основе базовых схем можно получить различные виды фильтров как простейших, так и более сложных. а) б) Активные фильтры 2 - го порядка: а) ФНЧ; б) ФВЧ
Активные фильтры На основе базовых схем можно получить различные виды фильтров как простейших, так и более сложных. а) б) Активные фильтры 2 - го порядка: а) ФНЧ; б) ФВЧ
 Активные фильтры Частота среза активного ФНЧ 2 - го порядка будет определяться из выражения . . . . (7) Активный фильтр верхних частот 2 - го порядка может быть построен перестановкой местами резисторов и конденсаторов в схеме фильтра нижних частот. Частота среза при этом будет определяться по формуле . . . . (8)
Активные фильтры Частота среза активного ФНЧ 2 - го порядка будет определяться из выражения . . . . (7) Активный фильтр верхних частот 2 - го порядка может быть построен перестановкой местами резисторов и конденсаторов в схеме фильтра нижних частот. Частота среза при этом будет определяться по формуле . . . . (8)
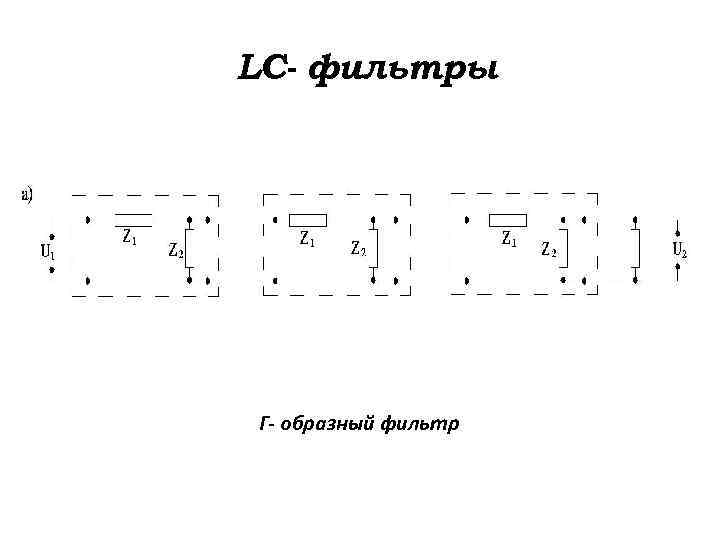 LC- фильтры Г- образный фильтр
LC- фильтры Г- образный фильтр
 LC- фильтры Т- образный фильтр
LC- фильтры Т- образный фильтр
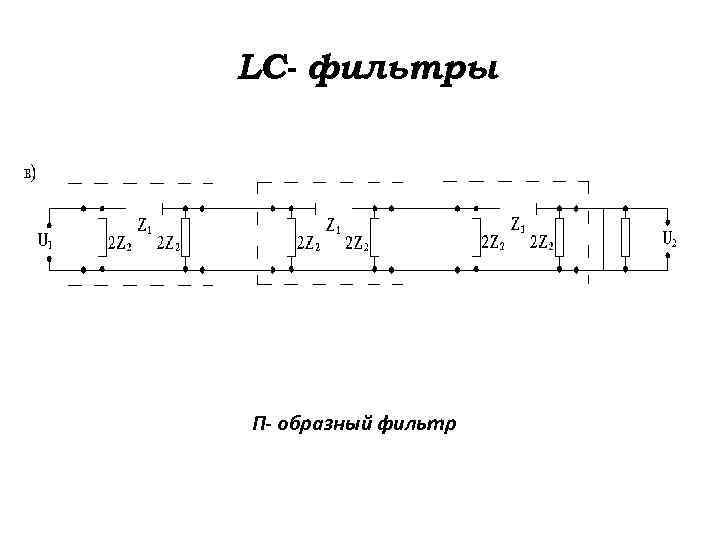 LC- фильтры П- образный фильтр
LC- фильтры П- образный фильтр
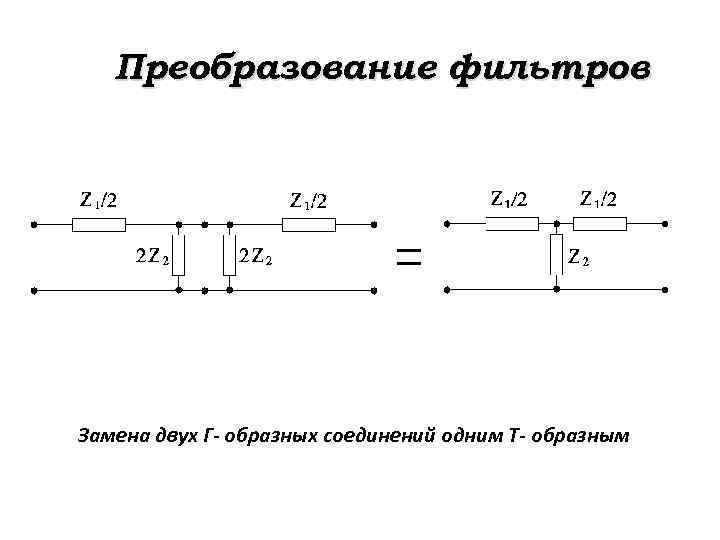 Преобразование фильтров Замена двух Г- образных соединений одним Т- образным
Преобразование фильтров Замена двух Г- образных соединений одним Т- образным
 Преобразование фильтров Замена двух Г- образных соединений одним П- образным
Преобразование фильтров Замена двух Г- образных соединений одним П- образным
 Преобразование фильтров Все сопротивления звеньев должны быть реактивными и иметь высокую добротность, чтобы фильтр как можно меньше ослаблял сигнал в полосе прозрачности. Если произведение Z 1 Z 2 не зависит от частоты, т. е. Z 1 Z 2 = k 2, где k – постоянная величина, то такой фильтр называется фильтром типа k. В нём одно из сопротивлений индуктивное, а другое – ёмкостное, например: а или а
Преобразование фильтров Все сопротивления звеньев должны быть реактивными и иметь высокую добротность, чтобы фильтр как можно меньше ослаблял сигнал в полосе прозрачности. Если произведение Z 1 Z 2 не зависит от частоты, т. е. Z 1 Z 2 = k 2, где k – постоянная величина, то такой фильтр называется фильтром типа k. В нём одно из сопротивлений индуктивное, а другое – ёмкостное, например: а или а
 Параметры. LC- фильтра Основными качественными показателями фильтра являются затухание и частотная характеристика. . . . (9)
Параметры. LC- фильтра Основными качественными показателями фильтра являются затухание и частотная характеристика. . . . (9)
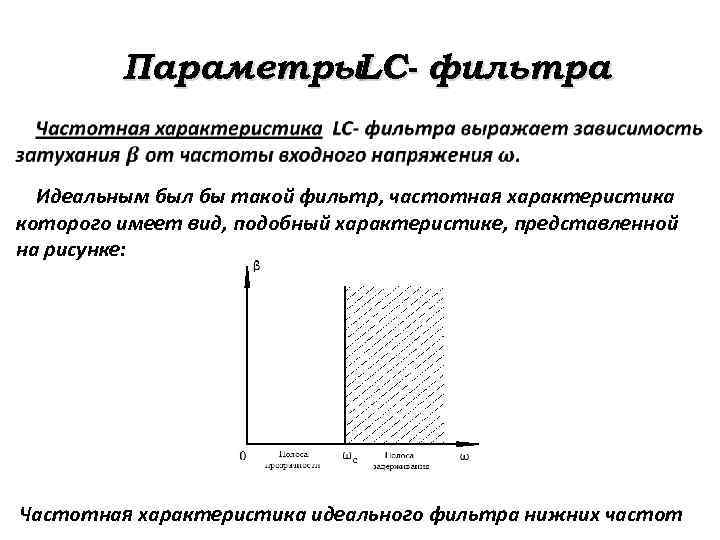 Параметры. LC- фильтра Идеальным был бы такой фильтр, частотная характеристика которого имеет вид, подобный характеристике, представленной на рисунке: Частотная характеристика идеального фильтра нижних частот
Параметры. LC- фильтра Идеальным был бы такой фильтр, частотная характеристика которого имеет вид, подобный характеристике, представленной на рисунке: Частотная характеристика идеального фильтра нижних частот
 Согласование фильтра с нагрузкой Входное сопротивление фильтра, согласованного во всех сечениях, называется характеристическим, или волновым сопротив -лением фильтра и обозначается буквой Z 0. Эквивалентные схемы звеньев фильтров, согласованных с нагрузкой
Согласование фильтра с нагрузкой Входное сопротивление фильтра, согласованного во всех сечениях, называется характеристическим, или волновым сопротив -лением фильтра и обозначается буквой Z 0. Эквивалентные схемы звеньев фильтров, согласованных с нагрузкой
 Характеристические сопротивления фильтров Формулы характеристических сопротивлений Т- и П- образных фильтров можно вывести исходя из того, что входное сопротивление каждого звена фильтра, нагруженного на характеристическое сопротивление, равно этому сопротивлению. Характеристическое сопротивление Т- образного фильтра, согласно рис. а, равно . . . (10)
Характеристические сопротивления фильтров Формулы характеристических сопротивлений Т- и П- образных фильтров можно вывести исходя из того, что входное сопротивление каждого звена фильтра, нагруженного на характеристическое сопротивление, равно этому сопротивлению. Характеристическое сопротивление Т- образного фильтра, согласно рис. а, равно . . . (10)
 Характеристические сопротивления фильтров Аналогично можно доказать, что характеристическое сопротивление П- образного фильтра (рис. б) равно: . . . . (11)
Характеристические сопротивления фильтров Аналогично можно доказать, что характеристическое сопротивление П- образного фильтра (рис. б) равно: . . . . (11)
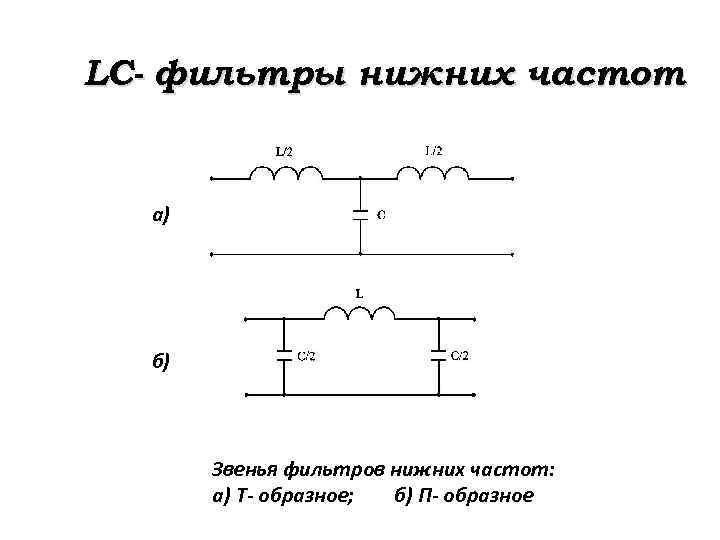 LC- фильтры нижних частот а) б) Звенья фильтров нижних частот: а) Т- образное; б) П- образное
LC- фильтры нижних частот а) б) Звенья фильтров нижних частот: а) Т- образное; б) П- образное
 LC- фильтры нижних частот В каждом из этих звеньев сопротивления и Характеристическое сопротивление Т- образного фильтра = = = . . (12)
LC- фильтры нижних частот В каждом из этих звеньев сопротивления и Характеристическое сопротивление Т- образного фильтра = = = . . (12)
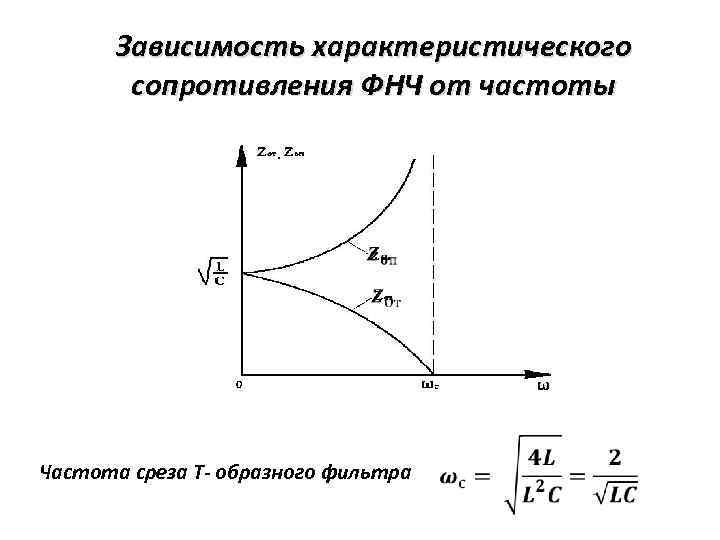 Зависимость характеристического сопротивления ФНЧ от частоты Частота среза Т- образного фильтра
Зависимость характеристического сопротивления ФНЧ от частоты Частота среза Т- образного фильтра
 Зависимость характеристического сопротивления ФНЧ от частоты Характеристическое сопротивление П- образного фильтра . . . . (13)
Зависимость характеристического сопротивления ФНЧ от частоты Характеристическое сопротивление П- образного фильтра . . . . (13)
 Зависимость характеристического сопротивления ФНЧ от частоты
Зависимость характеристического сопротивления ФНЧ от частоты
 Расчёт элементов ФНЧ Элементы фильтра L и С рассчитываются по заданным частоте среза Учитывая, что и находим: …. . . . (14) . . . . (15)
Расчёт элементов ФНЧ Элементы фильтра L и С рассчитываются по заданным частоте среза Учитывая, что и находим: …. . . . (14) . . . . (15)
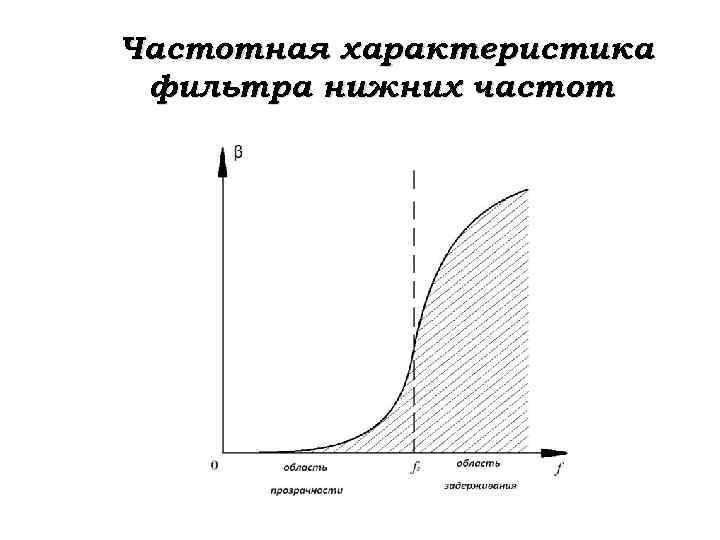 Частотная характеристика фильтра нижних частот
Частотная характеристика фильтра нижних частот
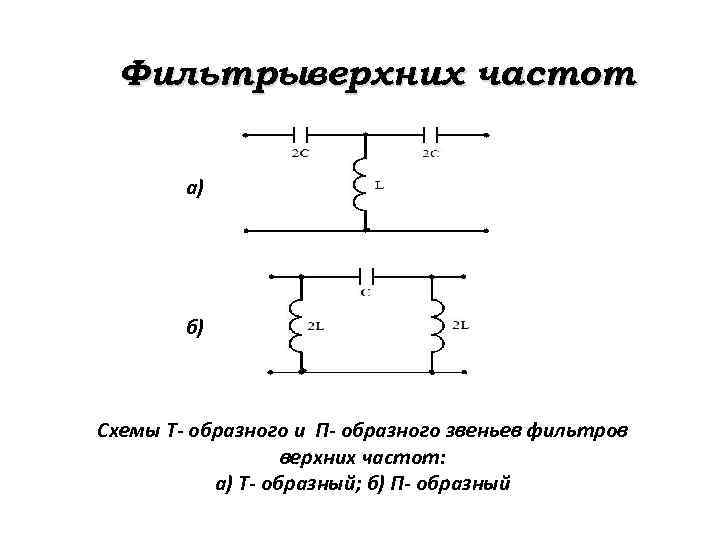 Фильтрыверхних частот а) б) Схемы Т- образного и П- образного звеньев фильтров верхних частот: а) Т- образный; б) П- образный
Фильтрыверхних частот а) б) Схемы Т- образного и П- образного звеньев фильтров верхних частот: а) Т- образный; б) П- образный
 Характеристическое сопротивление Т- образного фильтра В данном случае Подставляя и и в формулы (10) и (11), можно найти характеристическое сопротивление Т- образного фильтра: . . . . (16)
Характеристическое сопротивление Т- образного фильтра В данном случае Подставляя и и в формулы (10) и (11), можно найти характеристическое сопротивление Т- образного фильтра: . . . . (16)
 Характеристическое сопротивление П- образного фильтра: . . . . (17)
Характеристическое сопротивление П- образного фильтра: . . . . (17)
 Частота среза ФВЧ На нижних частотах, где ФВЧ «непрозрачен» , характеристические и сопротивления имеют мнимую величину (т. е. реактивный характер). И только на частотах, бóльших частоты среза, эти сопротивления становятся активными. На частоте среза откуда , . . . . (18)
Частота среза ФВЧ На нижних частотах, где ФВЧ «непрозрачен» , характеристические и сопротивления имеют мнимую величину (т. е. реактивный характер). И только на частотах, бóльших частоты среза, эти сопротивления становятся активными. На частоте среза откуда , . . . . (18)
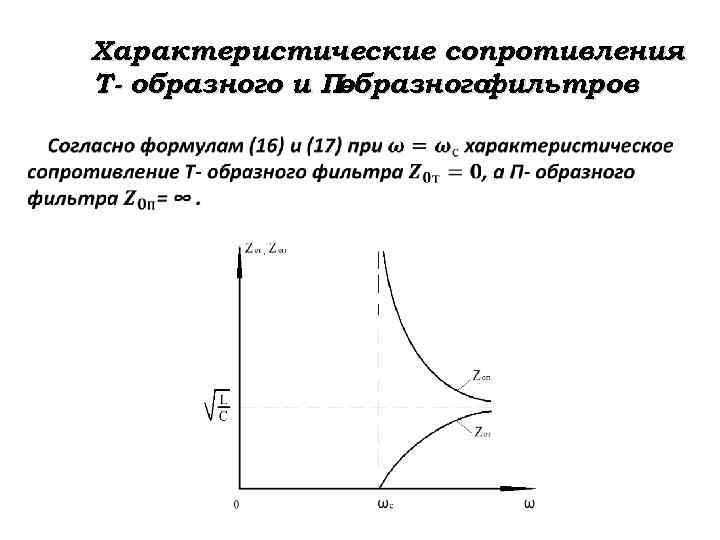 Характеристические сопротивления Т- образного и Побразного фильтров
Характеристические сопротивления Т- образного и Побразного фильтров
 Характеристические сопротивления Т- образного и П- образного фильтров , . . (19)
Характеристические сопротивления Т- образного и П- образного фильтров , . . (19)
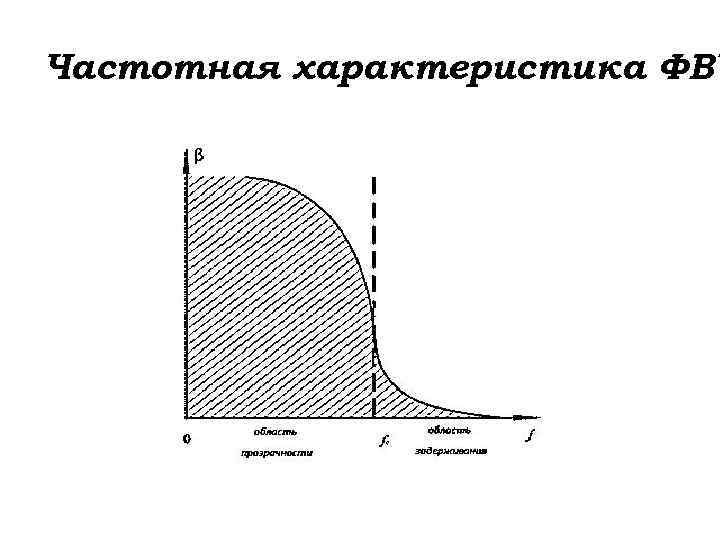 Частотная характеристика ФВЧ
Частотная характеристика ФВЧ
 Расчёт элементов ФВЧ Из выражений (18) и (19) следуют соотношения для расчёта индуктивностей и ёмкостей фильтра верхних частот: . . . . (20) . . . . (21)
Расчёт элементов ФВЧ Из выражений (18) и (19) следуют соотношения для расчёта индуктивностей и ёмкостей фильтра верхних частот: . . . . (20) . . . . (21)
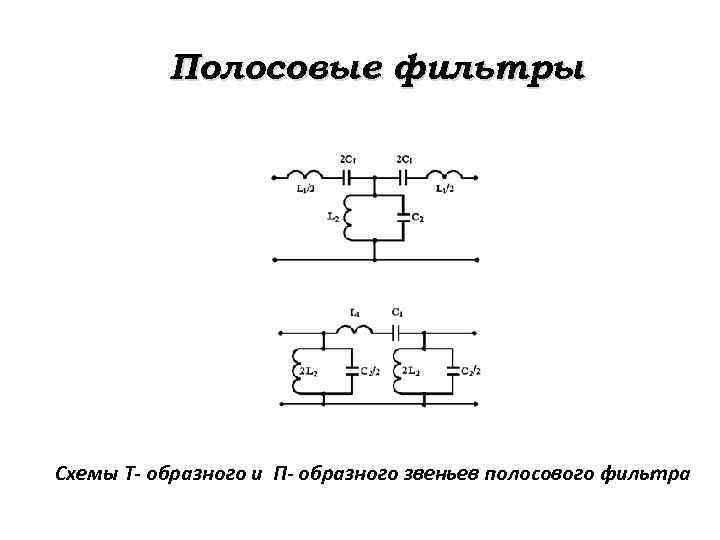 Полосовые фильтры Схемы Т- образного и П- образного звеньев полосового фильтра
Полосовые фильтры Схемы Т- образного и П- образного звеньев полосового фильтра
 Полосовыефильтры . . (22) Поэтому отношение является постоянной величиной. . . . . (23)
Полосовыефильтры . . (22) Поэтому отношение является постоянной величиной. . . . . (23)
 Полосовые фильтры Разность частот среза, т. е. полоса прозрачности ПФ, равна . . (24) . . (25)
Полосовые фильтры Разность частот среза, т. е. полоса прозрачности ПФ, равна . . (24) . . (25)
 Полосовые фильтры Из выражений (16) и (17) можно определить формулы для расчёта элементов фильтра }. . . . . (26)
Полосовые фильтры Из выражений (16) и (17) можно определить формулы для расчёта элементов фильтра }. . . . . (26)
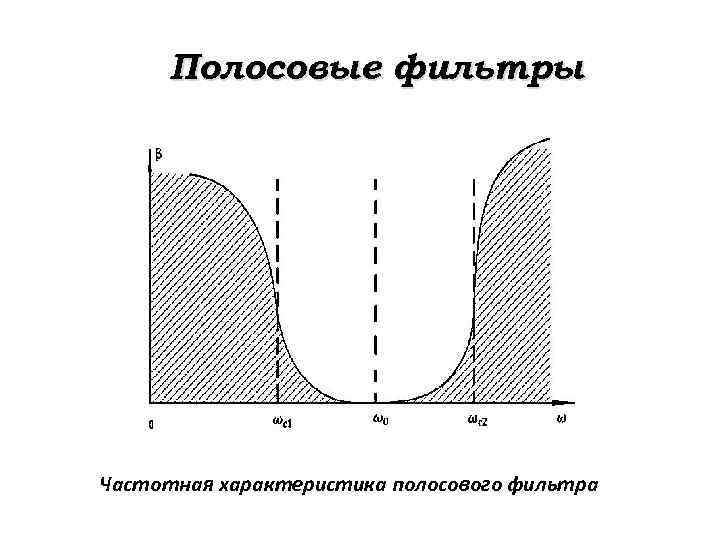 Полосовые фильтры Частотная характеристика полосового фильтра
Полосовые фильтры Частотная характеристика полосового фильтра
 Полосовые фильтры
Полосовые фильтры
 Режекторные (заграждающие) фильтры
Режекторные (заграждающие) фильтры
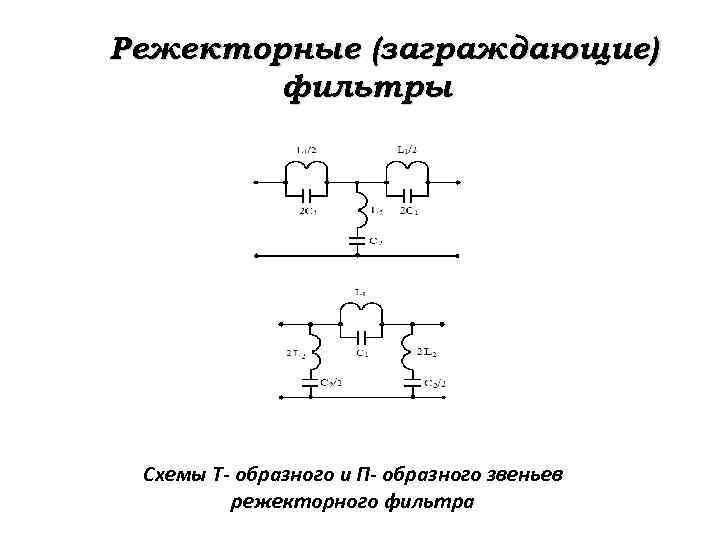 Режекторные (заграждающие) фильтры Схемы Т- образного и П- образного звеньев режекторного фильтра
Режекторные (заграждающие) фильтры Схемы Т- образного и П- образного звеньев режекторного фильтра
 Режекторные (заграждающие) фильтры
Режекторные (заграждающие) фильтры
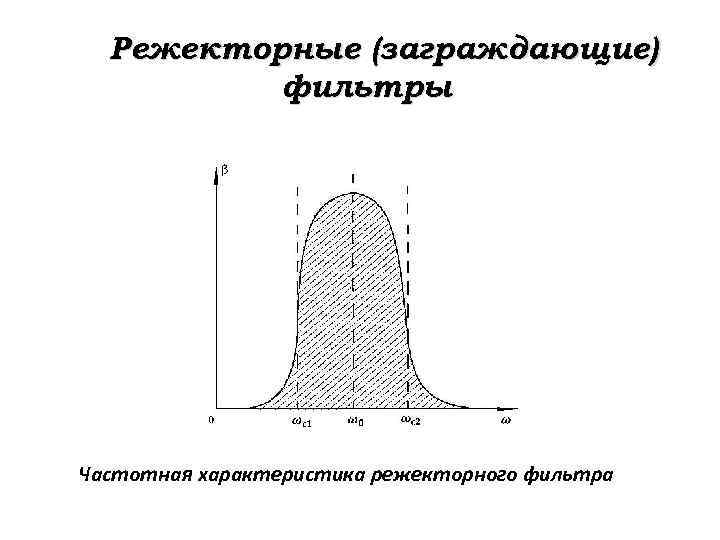 Режекторные (заграждающие) фильтры Частотная характеристика режекторного фильтра
Режекторные (заграждающие) фильтры Частотная характеристика режекторного фильтра
 Фильтры на поверхностных акустических волнах (ПАВ) Поверхностные акустические волны (ПАВ) — это упругие (необъёмные) волны, распространяющиеся с невысокой скоростью вдоль свободной поверхности твёрдого тела или вдоль границы твёрдого тела с другими средами и затухающие при удалении от границ. В качестве среды распространения используются различные пьезоэлектрические монокристаллы: кварц, ниобат лития, танталат лития, германат висмута и др.
Фильтры на поверхностных акустических волнах (ПАВ) Поверхностные акустические волны (ПАВ) — это упругие (необъёмные) волны, распространяющиеся с невысокой скоростью вдоль свободной поверхности твёрдого тела или вдоль границы твёрдого тела с другими средами и затухающие при удалении от границ. В качестве среды распространения используются различные пьезоэлектрические монокристаллы: кварц, ниобат лития, танталат лития, германат висмута и др.
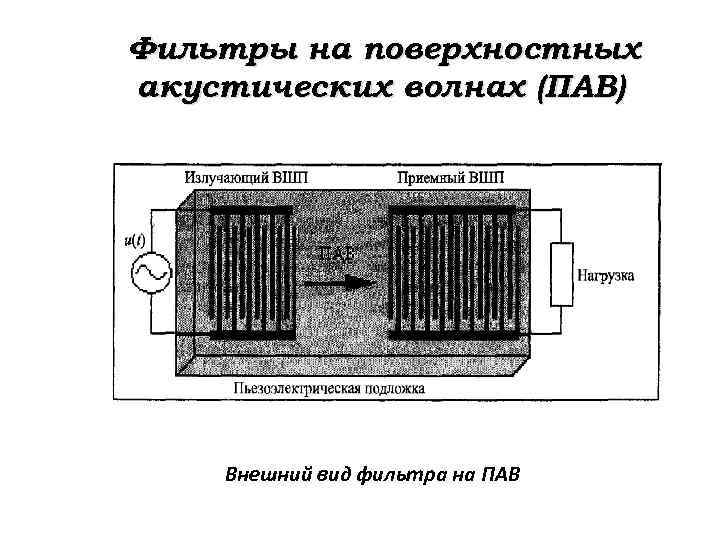 Фильтры на поверхностных акустических волнах (ПАВ) Внешний вид фильтра на ПАВ
Фильтры на поверхностных акустических волнах (ПАВ) Внешний вид фильтра на ПАВ


