Radioactivity Types of particles Alpha particles Two

Radioactivity Types of particles: Alpha particles • Two protons + two neutrons • Same as helium-4 nucleus • + 2 charge; deflected by a magnetic field, and attracted to negative charges

Alpha particles • Largest particle of radioactivity • Short range • Stopped by sheet of paper • Most damaging due to large mass Alpha tracks in a cloud chamber

Nuclear equations • Mass must be conserved • Mass numbers and atomic numbers must have same sum on each side of equation • Result of alpha emission: mass number decreases by 4, atomic number decreases by 2 • Note symbol for alpha particle – sometimes written 42 a or just a

Beta Particles • Consist of free electrons • Low mass, -1 charge • Medium range, medium penetrating power • Stopped by thick wood, thin sheet of lead b • Symbol is the Greek letter beta or 0 -1 e • Produced by a neutron, which turns into a proton

Nuclear equations • In beta decay a neutron turns into a proton and ejects an electron • Mass number does not change, and atomic number increases by 1 • Example of transmutation

Gamma Radiation • Consists of highenergy photons • No rest mass, no charge • Not deflected by magnetic field • Long range, very penetrating • Accompanies many other types of decay g • Symbol is Greek letter gamma • Only product of IT – internal transition • Produces no change of mass or atomic numbers

Other types of decay Positron Emission • Positrons are the electron’s antiparticle • Same characteristics as electron, except for positive charge • Symbol: b+ or 01 e Positron Emission Tomography (PET scan)

Positron emission • In positron emission a proton ejects a positron and becomes a neutron • Mass number does not change • Atomic number decreases by one

Electron Capture • If there are too many protons in a nucleus, it may capture an electron • A proton becomes a neutron Symbol for an electron

Electron capture • Mass number stays the same • Atomic number decreases by one • Same result as positron emission

Nuclear Stability • Nuclear particles (protons and neutrons) are called nucleons • Nucleons are held together by nuclear strong force (short range, very strong) • Neutrons are “glue” – necessary to hold the nucleus together • Without neutrons the nucleus would fly apart due to electrostatic repulsion

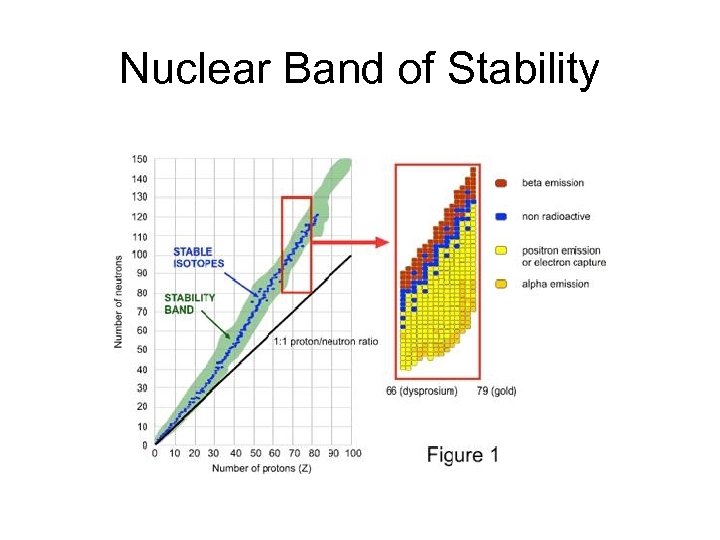Nuclear Band of Stability

Stability and Decay • Above the stability band: Too many neutrons • Beta decay reduces the neutron/proton ratio • Very large nuclei (Z>83) undergo alpha decay, which reduces the size of the nucleus

Stability and decay • Below the band of stability: too many protons • Positron emission or electron capture • Protons are reduced, neutrons increased 1 p 1 n + 0 b 1 0 1 1 1 p + 0 -1 e 1 0 n

Nuclear Magic Numbers • Nuclei with certain numbers of protons or neutrons are especially stable • “Magic numbers” are 2, 8, 20, 28, 50, 82, and 126 • When both neutrons and protons are magic numbers, the nucleus is specially stable: 20882 Pb

Nuclear Magic Numbers • Most stable nuclei have the same “magic number” of protons and neutrons: 42 He, 16 O, and 40 Ca 8 20 • “Even-odd” rule: Nuclei with even numbers of protons and neutrons are more stable than odds: • Stable isotopes: 264 • Both even: 157 Both odd: 5

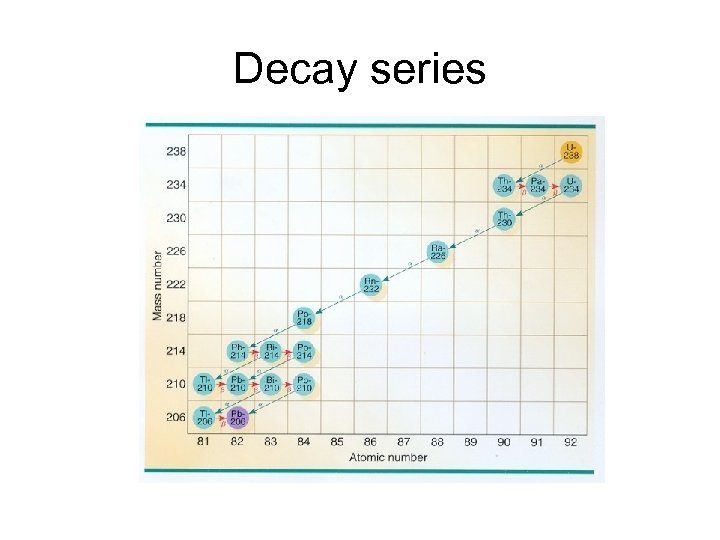Decay series

Induced Transmutation • Transmutation can be induced by allowing high-energy particles to strike atomic nuclei 4 He + 14 N 17 O + 1 p 2 7 8 1 238 U + 1 n 239 U 239 Np + 0 e 92 0 92 93 -1 239 Np 239 Pu + 0 e 93 94 -1 1 n + 147 N 146 C + 11 H 0

Radioactive decay Radioactive Decay • Radioactive isotopes decay at predictable rates • Half Life: the time it takes for 1/2 of a sample to decay • Half of the remaining sample decays every half life period

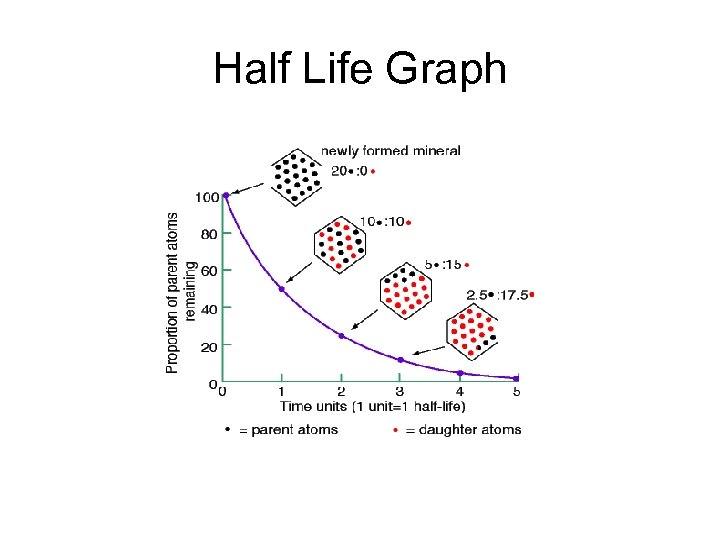Half Life Graph

Half Life • Follows exponential decay • Moment of decay of any one particle is unpredictable • Example: Radon-222 decays with a half life of 3. 8 days. Approximately how long will it take for 9. 5 grams of a 10 gram sample to decay?

Half Life Problems • Solution: Divide sample mass in half until 0. 5 grams or less is reached. 10/2 = 5 (one half life) 5/2 = 2. 5 (two half lives) 2. 5/2 = 1. 25 (three half lives) 1. 25/2 = 0. 625 (four half lives) 0. 625/2 = 0. 3125 (five half lives)

Half life Problems • Four half lives = 4 HL x 3. 8 days/HL = 15. 2 days • Five half lives = 5 HL x 3. 8 days/HL = 19 days • Therefore, 9. 5 grams of a 10 gram sample will decay in somewhere between 15. 2 and 19 days.

Half Life Problems • Example #2: Sally has a 15. 0 g sample of phosphorus-32 (half life 14. 28 days). About how much will be left two months later (60 days)? • Find time in half-lives: 60 days/14. 28 days/HL = 4. 20 half lives. • Multiply the sample mass by (1/2)y, where y = number of half-lives (use xy key on calculator)

Half Life Problems • 15. 0 g(1/2)4. 20 = 15. 0 g(0. 0544) = 0. 816 g remaining • Half life equation: Nt = N 0(1/2)t/t 1/2 or Nt = N 0 e-lt where l is the decay constant t = (t 1/2/0. 693)ln(N 0/Nt) Nuclear Reactions and Energy • Mass is not strictly conserved in nuclear reactions • Some mass is lost as energy

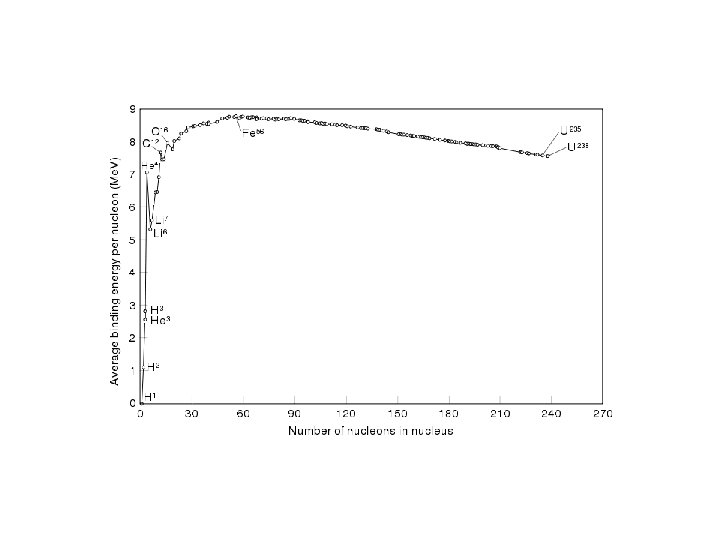
Nuclear Reactions and Energy • Mass to energy conversion is governed by DE = Dmc 2, where c = the speed of light in a vacuum (3. 0 x 108 m/s) • Nuclear binding energy is the energy lost when the nucleus is formed. • Mass equivalent of the nuclear binding energy is the mass defect. • Protons and neutrons in the nucleus have less mass than separate nucleons

Calculating Binding Energy • • • Example: Mass of 1 proton = 1. 00735 amu Mass of 1 neutron = 1. 00875 amu Mass of 1 electron = 0. 0005485 amu If 1 amu = 1. 66 x 10 -24 g, calculate the binding energy of an atom of helium-4 (mass 4. 00260325415 amu)

Binding energy of helium-4 • Mass of constituents Protons: 1. 00735 amu/p(2 p) = 2. 01470 amu Neutrons: 1. 00875 amu/n(2 n) = 2. 01750 amu Electrons: 0. 0005485 amu/e(2 e) = 0. 001097 amu Total: 4. 03330 amu(1. 66 x 10 -24 g/amu) = 6. 70 x 10 -24 g Helium atom: 4. 0026 amu(1. 66 x 10 -24 g/amu) = 6. 64 x 10 -24 g)

Binding energy of helium-4 • Mass deficit = 6. 70 x 10 -24 g - 6. 64 x 10 -24 g = 0. 06 x 10 -24 g = 6 x 10 -26 g = 6 x 10 -29 kg • Binding energy: DE = Dmc 2 • DE = 6 x 10 -29 kg(3. 00 x 108 m/s)2 = 5 x 10 -12 J • Energy per gram: one gram of helium-4 would have 1 g/(6. 64 x 10 -24) = 1. 51 x 1023 atoms • 1. 51 x 1023 a/g(5 x 10 -12 J/a) = 8 x 1011 J/g

Binding energy of helium-4 • • 8 x 1011 J/g(1 k. W-hr/3600 J) = 2 x 108 k. W-hr Average household uses 10, 656 k. W-hr/yr 2 x 108 k. W-hr/10, 656 k. W-hr/(house-yr) = 20, 000 Binding energy in one gram of helium-4 could power 20, 000 average households for one year • Alternatively, it could power one house for 20, 000 years, or Al Gore’s mansion for 904 years.

Nuclear Fission • Some larger nuclei will split into two parts when struck by a neutron • The two smaller nuclei are more stable, so energy is released • The two smaller nuclei will have a higher binding energy per nucleon • Neutrons are also released, producing a chain reaction

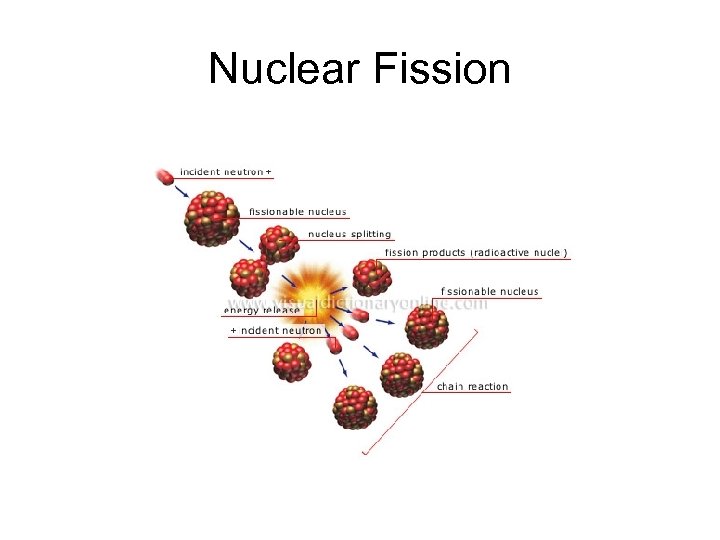Nuclear Fission

Nuclear chain reactions • Occur if the product of the reaction is necessary to start new reactions 1 n + 23592 U --> 23692 U --> 9236 Kr + 14156 Ba + 310 n 0 • Critical mass - minimum mass necessary to sustain a chain reaction • Large enough critical mass will explode

Nuclear Power Plants • Nuclear fuel is usually a supercritical mass of U-235 enriched uranium • Reaction is promoted by a moderator - a material that slows neutrons down so they will cause fission - usually carbon or D 2 O Nuclear reactor at Chernobyl

Nuclear Power Plants • Reaction is controlled by control rods (cadmium or boron), which absorb neutrons • Reaction generates heat, which makes steam to run a turbine CROCUS, a small research nuclear reactor

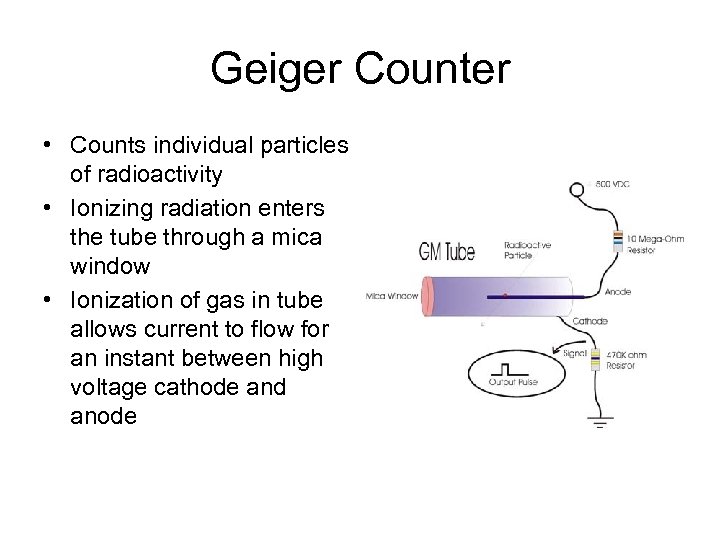Geiger Counter • Counts individual particles of radioactivity • Ionizing radiation enters the tube through a mica window • Ionization of gas in tube allows current to flow for an instant between high voltage cathode and anode