Рациональные числа Рациональные числа это числа

Рациональные числа § Рациональные числа – это числа вида , где m – целое число, а n – натуральное число. § Рациональные числа – это все целые числа, а также положительные и отрицательные обыкновенные дроби. § Десятичная дробь рассматривается как частный случай обыкновенной дроби. § 3=3, 000… § 5, 67=5, 67000… бесконечные периодические дроби. § = 0, 2666…. Период – повторяющаяся группа цифр после запятой. Любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби. (Обратное утверждение) Любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби. У периодической десятичной дроби период может быть любой длины.

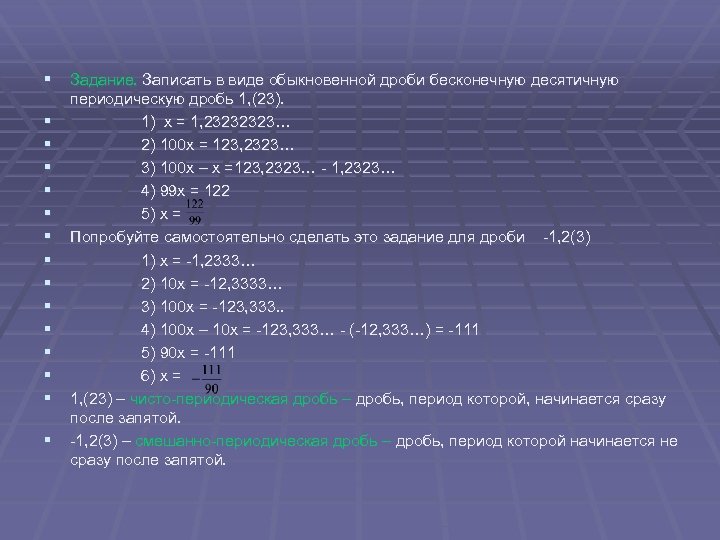§ Задание. Записать в виде обыкновенной дроби бесконечную десятичную § § § § периодическую дробь 1, (23). 1) х = 1, 2323… 2) 100 х = 123, 2323… 3) 100 х – х =123, 2323… - 1, 2323… 4) 99 х = 122 5) х = Попробуйте самостоятельно сделать это задание для дроби -1, 2(3) 1) х = -1, 2333… 2) 10 х = -12, 3333… 3) 100 х = -123, 333. . 4) 100 х – 10 х = -123, 333… - (-12, 333…) = -111 5) 90 х = -111 6) х = 1, (23) – чисто-периодическая дробь – дробь, период которой, начинается сразу после запятой. -1, 2(3) – смешанно-периодическая дробь – дробь, период которой начинается не сразу после запятой.

Тема «Рациональные числа» § § Домашнее задание. 2. 4. Среди правильных дробей вида к числу: а) , б). , где n – натуральное число, найдите ближайшую 2. 10. Запишите обыкновенную дробь в виде бесконечной десятичной периодической дроби: 2. 13 Запишите число в виде обыкновенной несократимой дроби: а) 0, (36); б) 12, 0(006); в) -0, 01(234).

Иррациональные числа § § § Домашнее задание: 3. 1. Докажите иррациональность числа: а) ; б) Составьте квадратное уравнение с целыми коэффициентами, у которого один из корней равен: а) ; б) 3. 19. Могут ли длины сторон треугольника выражаться числами: а) б)