Работу выполнила ученица 9 класса МБОУ ВСОШ

Зарегистрируйтесь, чтобы просмотреть полный документ!

Работу выполнила ученица 9 класса МБОУ ВСОШ № 2 Уразова Диляра Научные руководители Аксанова И. И. Насырова Н. И.

Ø изучить сжимающие аффинные преобразования; Ø изучить системы итерированных функций; Ø изучить применение систем итерированных функций для построения фракталов; Ø найти системы итерированных функций для ранее построенных геометрическим способом фракталов.

Ø изучить аффинные преобразования на плоскости; Ø изучить теорему о задании аффинного преобразования; Ø познакомиться с аналитическим заданием аффинного преобразования; Ø изучить процесс итерирования двумерных отображений; Ø изучить процесс итерации системы функций; Ø изучить понятие сжимающего отображения; Ø изучить понятие расстояния между множествами; Ø найти СИФы для фрактала «Журавлиный клин» и серии фракталов «Жемчужинки Востока» .

Аффинные преобразования обладают следующими важными свойствами: 1. При аффинном преобразовании прямая переходит в прямую, при этом параллельные прямые переходят в параллельные; 2. При аффинном преобразовании полуплоскость переходит в полуплоскость. 3. При аффинном преобразовании луч переходит в луч. 4. При аффинном преобразовании отрезок переходит в отрезок. 5. При аффинном преобразовании угол переходит в угол.

Итерирование двумерных отображений

Сжимающие отображения

Расстояние между множествами

Фракталы и системы итерированных функций Любое аффинное преобразование можно записать в виде f(x; y)=(ax+by+e; cx+dy+g)

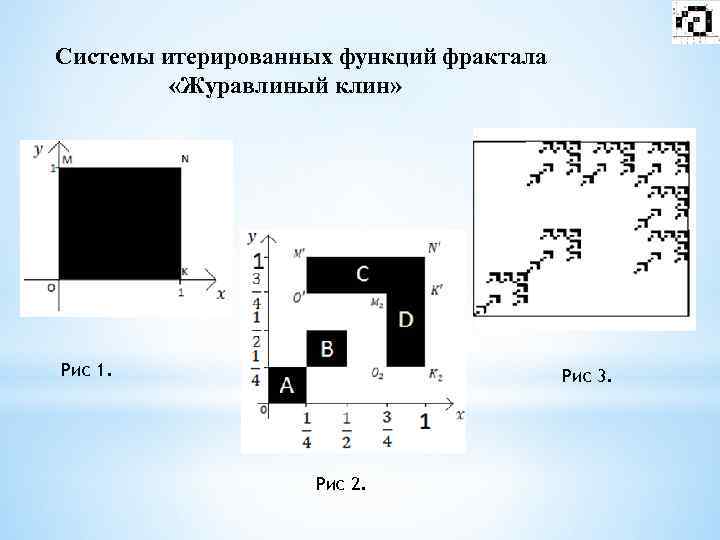
Системы итерированных функций фрактала «Журавлиный клин» Рис 1. Рис 3. Рис 2.

Фракталы и их СИФы Браслет Шахерезады Серьги Гюльчатай

Локон Сююмбике Кулон Надим

Заколка Алтынчеч

В данной исследовательской работе были изучены сжимающие аффинные преобразования и способ построения фракталов с помощью систем итерированных функций. В исследовательской работе самостоятельно найдены системы итерированных функций для фрактала « Журавлиный клин» и серии фракталов «Жемчужинки Востока» , которые ранее были построены геометрическим способом в работе «Построение геометрических фракталов на плоскости» .

1. Р. М. Кроновер. Фракталы и хаос в динамических системах. Основы теории. Москва: Постмаркет, 2000. -352 с. 2. А. Д. Морозов. Введение в теорию фракталов. Москва – Ижевск: Институт компьютерных исследований, 2004. 160 стр. 3. Л. С. Атанасян. , В. Т. Базылев. Геометрия. В 2 -х ч. Ч. I. М. : Просвещение, 1986. -336 с. 4. http: //ru. wikipedia. org/wiki/фрактал 5. http: //project. 1 september. ru/works/608653 6. http: //ghcube. com/

Скачать презентацию Работу выполнила ученица 9 класса МБОУ ВСОШ

применение СИФ.pptx

Количество слайдов: 21