Работу выполнил ст гр ПНГ-09 Осипенко Д О

Работу выполнил ст. гр. ПНГ-09 Осипенко Д. О.

Распознавание образов, научное направление, связанное с разработкой принципов и построением систем, предназначенных для определения принадлежности данного объекта к одному из заранее выделенных классов объектов. Под объектами в Распознавание образов понимают различные предметы, явления, процессы, ситуации, сигналы. Каждый объект описывается совокупностью основных характеристик (признаков, свойств) Х = (x 1, . . . , xi , . . . , xn), где i-я координата вектора Х определяет значения i-й характеристики, и дополнительной характеристикой S, которая указывает на принадлежность объекта к некоторому классу (образу). Набор заранее расклассифицированных объектов, т. е. таких, у которых известны характеристики Х и S, используется для обнаружения закономерных связей между значениями этих характеристик и поэтому называются обучающей выборкой. Те объекты, у которых характеристика S неизвестна, образуют контрольную выборку. Отдельные объекты обучающей и контрольной выборок называются реализациями.

Как распознавание образов связанно с геофизикой?

Одна из основных задач Распознавание образов — выбор правила (решающей функции) D, в соответствии с которым по значению контрольной реализации Х устанавливается её принадлежность к одному из образов, т. е. указываются «наиболее правдоподобные» значения характеристики S для данного Х. Выбор решающей функции D требуется произвести так, чтобы стоимость самого распознающего устройства, его эксплуатации и потерь, связанных с ошибками распознавания, была минимальной.

Примером задачи Распознавание образов этого типа может служить задача различения нефтеносных и водоносных пластов по косвенным геофизическим данным. По этим характеристикам сравнительно легко обнаружить пласты, насыщенные жидкостью. Значительно сложнее определить, наполнены они нефтью или водой. Требуется найти правило использования информации, содержащейся в геофизических характеристиках, для отнесения каждого насыщенного жидкостью пласта к одному из двух классов — водоносному или нефтеносному. При решении этой задачи в обучающую выборку включают геофизические данные вскрытых пластов.

Сходство или различие между объектами классификации устанавливается в зависимости от выбранного метрического расстояния между ними. Если каждый объект описывается свойствами (признаками), то он может быть представлен как точка в -мерном пространстве, и сходство с другими объектами будет определяться как соответствующее расстояние. При классификации используются различные меры расстояния между объектами.

Для каждого класса по обучающей выборке строится эталон, имеющий значения признаков где = K – количество объектов данного образа в обучающей выборке, i – номер признака. По существу, эталон – это усреднённый по обучающей выборке абстрактный объект (рис. 2). Абстрактным мы его называем потому, что он может не совпадать не только ни с одним объектом обучающей выборки, но и ни с одним объектом генеральной совокупности.

Распознавание осуществляется следующим образом. На вход системы поступает объект , принадлежность которого к тому или иному образу системе неизвестна. От этого объекта измеряются расстояния до эталонов всех образов, и система относит к тому образу, расстояние до эталона которого минимально. Расстояние измеряется в той метрике, которая введена для решения определённой задачи распознавания.

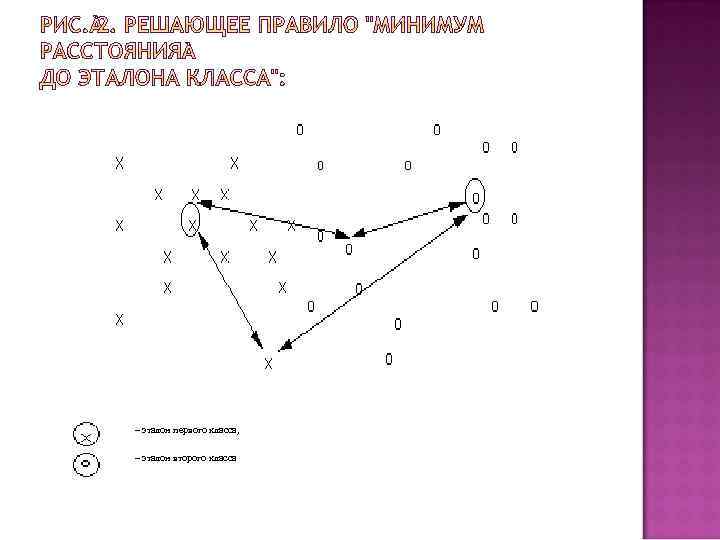
– эталон первого класса, – эталон второго класса

Процесс обучения состоит в следующем. На первом этапе в обучающей выборке " охватывают " все объекты каждого класса гиперсферой возможно меньшего радиуса. Сделать это можно, например, так. Строится эталон каждого класса. Вычисляется расстояние от эталона до всех объектов данного класса, входящих в обучающую выборку. Выбирается максимальное из этих расстояний. Строится гиперсфера с центром в эталоне и радиусом =+. Она охватывает все объекты данного класса. Такая процедура проводится для всех классов (образов). На рис. 3 приведён пример двух образов в двухмерном признаковом пространстве.

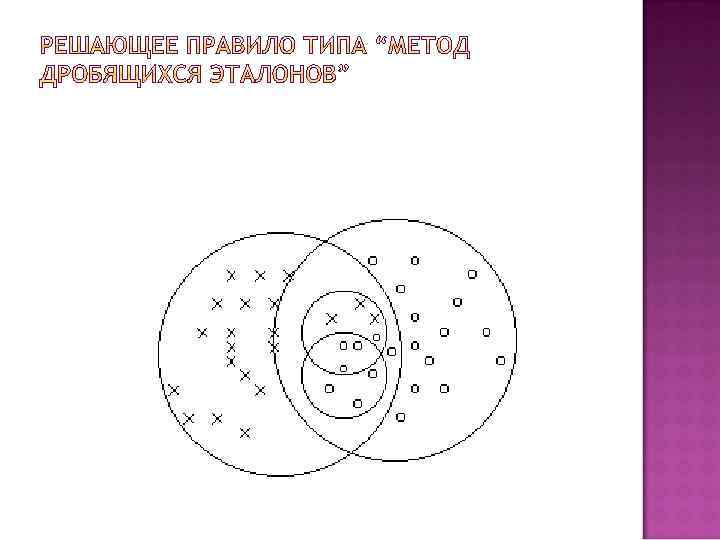
Если гиперсферы различных образов пересекаются и в области перекрытия оказываются объекты более чем одного образа, то для них строятся гиперсферы второго уровня, затем третьего и т. д. до тех пор, пока области не окажутся непересекающимися, либо в области пересечения будут присутствовать объекты только одного образа. Распознавание осуществляется следующим образом. Определяется местонахождение объекта относительно гиперсфер первого уровня. При попадании объекта в гиперсферу, соответствующую одному и только одному образу, процедура распознавания прекращается. Если же объект оказался в области перекрытия гиперсфер, которая при обучении содержала объекты более чем одного образа, то переходим к гиперсферам второго уровня и проводим действия такие же, как для гиперсфер первого уровня. Этот процесс продолжается до тех пор, пока принадлежность неизвестного объекта тому или иному образу не определится однозначно. Правда, это событие может и не наступить. В частности, неизвестный объект может не попасть ни в одну из гиперсфер какого-либо уровня. В этих случаях "учитель" должен включить в решающие правила соответствующие действия.

Например, система может либо отказаться от решения об однозначном отнесении объекта к какому-либо образу, либо использовать критерий минимума расстояния до эталонов данного или предшествующего уровня и т. п. Какой из этих приёмов эффективнее, сказать трудно, т. к. метод дробящихся эталонов носит в основном эмпирический характер.

Само название говорит о том, что граница, разделяющая в признаковом пространстве области различных образов, описывается линейной функцией

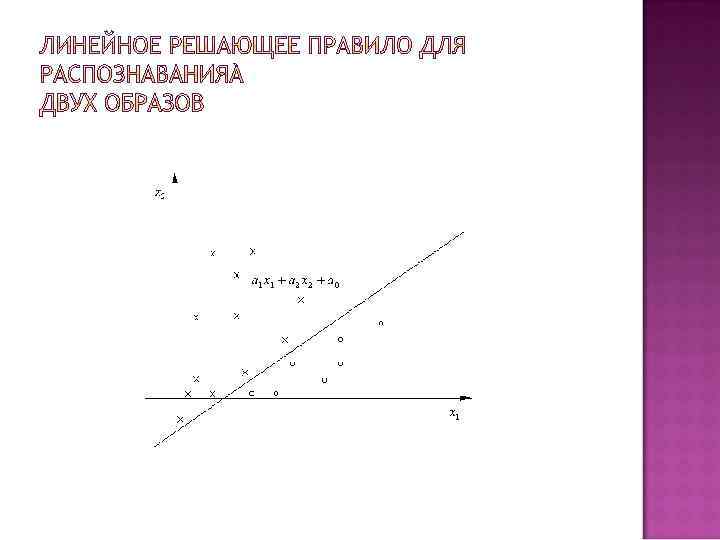
Одна граница при этом разделяет области двух образов. Если M>2, то требуется несколько линейных функций и граница является, вообще говоря, кусочно линейной. Для наглядности будем считать M=2. Если на множестве объектов выполняется условие

Параметрическое оценивание распределений реализуется в тех случаях, когда известен вид распределений и по обучающей выборке необходимо лишь оценить значения параметров этих распределений. Априорное знание вида на практике встречается нечасто, однако, учитывая удобство данного подхода, иной раз делают допущение, например, о том, что - нормальный закон. Такого рода допущения далеко не всегда имеют убедительные основания, но тем не менее используются, если результаты обучения приводят к приемлемым ошибкам распознавания.

Итак, обучение сводится к оценке значений параметров при заранее известном виде этих распределений. Особое место среди распределений занимает нормальный закон. Это связано с тем, что, как известно из математической статистики, если случайная величина порождена воздействием достаточно большого числа случайных факторов с произвольными законами распределения и среди этих влияний нет явно доминирующего, то интересующая нас величина имеет нормальный закон распределения. Для одномерного случая

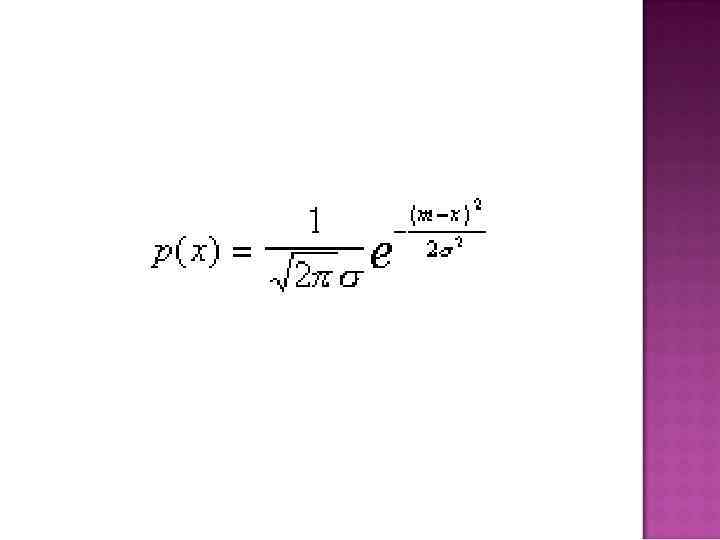
Параметрами этого распределения являются две величины: m–математическое ожидание, – дисперсия. Их-то и нужно оценить по выборке. Одним из наиболее простых является метод моментов. Он применим для распределений , зависящих от L параметров, имеющих L конечных первых моментов, которые могут быть выражены как явные функции параметров. Тогда, вычислив по выборке первых её моментов и приравняв их , получим систему уравнений

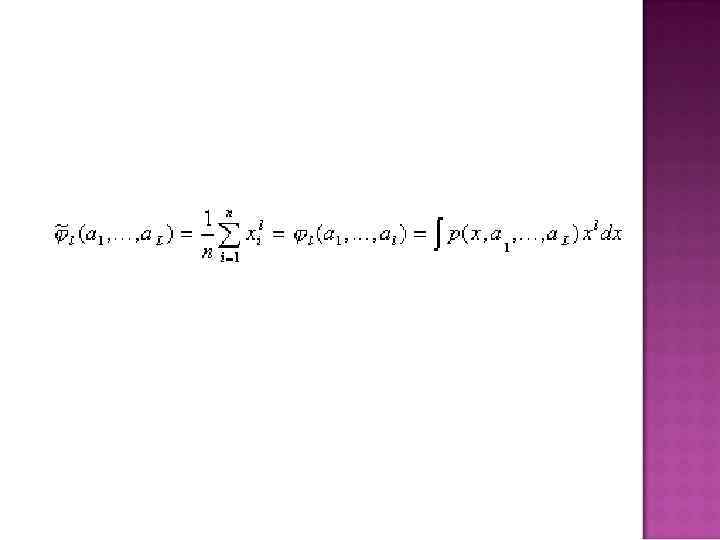
Это, пожалуй, наиболее часто используемая мера расстояния. Она является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:

где: – P расстояние между объектами А и B; – Ai значение i-свойства объекта A ; –Bi значение i -свойства объекта B. Естественное, с геометрической точки зрения, евклидова мера расстояния может оказаться бессмысленной, если признаки измерены в разных единицах. Чтобы исправить положение, прибегают к нормированию каждого признака. Применение евклидова расстояния оправдано в следующих случаях: свойства (признаки) объекта однородны по физическому смыслу и одинаково важны для классификации; признаковое пространство совпадает с геометрическим пространством.

Данная мера расстояния используется в тех случаях, когда требуется придать больше значение более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:

Спасибо за внимание!