412bad212052c013a59227ca86767669.ppt
- Количество слайдов: 44

РАБОТА С НЕСИГУРНИ ДАННИ И ЗНАНИЯ В СИСТЕМАТА GURU КОЕФИЦИЕНТИ НА ДОСТОВЕРНОСТ НА РАБОТНИТЕ ПРОМЕНЛИВИ GURU дава възможност да се определи увереността в стойността (стойностите) на дадена работна променлива. От своя страна степента на достоверност на всяка стойност на променлива може да се използва като фактор, който влияе на процеса на логически извод. Поради това решението, което се получава като резултат, зависи и от това, доколко потребителят е уверен по отношение на различни аспекти на проблема.

Мярката на увереност в стойността на дадена променлива се нарича коефициент (фактор) на достоверност на тази стойност. Коефициентът на достоверност е цяло число между 0 и 100, като 100 представя най-високата степен на достоверност, а 0 представя най-ниската.

Командата LET може да се използва за присвояване на желания коефициент на достоверност на (стойността на) всяка символна, числова или логическа работна променлива. В такъв случай командата LET има следния вид: LET <променлива> = <израз> CF <цяло число> Примери: LET ZAPLATA = 12000 CF 86 LET PROD = "принтер" CF 78 LET NAVREME = TRUE CF 54

Ако командата LET се използва за присвояване на стойност на променлива без едновременно посочване на коефициента й на достоверност, GURU дава автоматично на този коефициент на достоверност стойност 100.

РАЗМИТИ РАБОТНИ ПРОМЕНЛИВИ Размита променлива се нарича работна променлива или елемент на масив, който има (една или) няколко стойности, всяка със свой собствен коефициент на достоверност. Ако има неяснота (т. е. "размитост") относно точната стойност на дадена променлива, може да се даде възможност тя да притежава едновременно няколко стойности, всяка с определена степен на достоверност. Всяка размита променлива може да притежава до 255 различни стойности за даден момент.

За присвояване на множество от стойности на дадена размита променлива може да се използва отново командата LET. Примери: LET DOHOD = {13000 CF 46, 14000 CF 91, 15000 CF 48} LET VPROD = {"книги" CF 28, "моливи" CF 18, "телбод" CF 44, "хартия" CF 52} LET X = {514, "грозде", TRUE} CF 27

Редът, в който са изброени стойностите във фигурните скоби, е без значение. Допустимо е да се присвояват различни типове стойности на една размита променлива. Ако не се зададе коефициент на достоверност за някоя стойност на дадена размита променлива, GURU приема по премълчаване достоверност 100. Допустимо е да се присвоява еднакъв коефициент на достоверност на всички стойности на дадена размита променлива (виж последния пример по-горе).

Командата LET може да се използва също и за задаване на допълнителни стойности или за елиминиране на някои от съществуващите стойности на една размита променлива. Примери: LET DOHOD = {13000 CF 46, 14000 CF 91, 15000 CF 48} LET DOHOD += {16000 CF 14}

С последната команда се присвоява на размитата променлива DOHOD допълнителна стойност 16000 с коефициент на достоверност 14. Използването на знака + преди знака = означава, че се прибавят допълнителни стойности към вече съществуващите. Командата "+=" се нарича команда за добавящо присвояване.

Ако е необходимо да се елиминират някои от стойностите на дадена размита променлива, това може да стане чрез командата за т. нар. отнемащо присвояване. Например: LET VPROD -= {"книги", "телбод"}

ИЗРАЗИ И ОПЕРАТОРИ В СИСТЕМАТА GURU Изразите в GURU включват по една или повече променливи и/или константи, които най-често са от един и същ тип. Всеки израз може да съдържа и оператори, които определят как се получава неговата стойност. В зависимост от типа на участващите величини и използваните оператори даден израз може да има символна, числова, логическа или неопределена (UNKNOWN) стойност.

Символните, числовите и логическите изрази могат да имат свои коефициенти на достоверност. Ако даден израз съдържа поне една размита променлива, той също ще бъде размит. Когато GURU оценява такъв израз, той може да има множество от стойности, всяка от които със свой коефициент на достоверност.

Символни изрази Всеки символен израз се състои от една или повече символни константи и/или променливи. Основният символен оператор "+" се използва за означаване на операцията конкатенация на два символни низа.

Коефициенти на достоверност на символни изрази Ако даден символен израз съдържа само константи, той има коефициент на достоверност 100. Пример LET NEWDATE = "07/11" + "/1996" В този случай се оценява изразът от дясната страна на знака за равенство и получената стойност се присвоява на променливата NEWDATЕ с коефициент на достоверност 100.

Ако символният израз съдържа променливи, техните коефициенти на достоверност съвместно допринасят за резултатния коефициент на достоверност на оценения израз. Текущата стойност на променливата на средата E. CFJO определя как ще се изчислява резултатният коефициент на достоверност на израза. По-точно, резултатният коефициент на достоверност на израз, в който участват две променливи с коефициенти на достоверност съответно a и b, се получава по следния начин:

-------------------------------| Стойност | Описание | Метод за пресмятане | | на E. CFJO | | | -------------------------------| M | Минимум | min(a, b) | -------------------------------| P | Произведение | a*b/100 | -------------------------------| A | Средно | (min(a, b) + a*b/100)/2 | -------------------------------| B | Баланс | a*b/100 * (2 - max(a, b)/100) | --------------------------------

От тези четири метода винаги методът на минимума резултира в най-високия коефициент на достоверност, а методът на произведението - в найниския коефициент на достоверност. Средният метод дава средното аритметично от резултатите, които дават горните два метода. Стойностите, получени по метода на баланса, също са между стойностите, получени по методите на минимума и произведението.

Ако max(a, b)=50, методът на баланса дава същия резултат, както и методът на средното (средният метод). Ако max(a, b)<50, методът на баланса дава резултат, по-близък до резултата, получен по метода на произведението, отколкото до резултата, получен по метода на минимума. Ако max(a, b)>50, методът на баланса дава резултат, по-близък до резултата, получен по метода на минимума, отколкото до резултата, получен по метода на произведението.

По този начин, когато съществува висока достоверност, резултатът от балансовия метод се приближава до резултата, получен по метода на минимума. Обратно, когато не съществува висока достоверност, резултатът от балансовия метод се приближава до резултата, получен по метода на произведението.

Пример 1 Нека е зададена следната поредица от команди за присвояване: LET NEWDAY = "07/11" CF 40 LET NEWYR = "/1996" CF 60 LET NEWDATE = NEWDAY + NEWYR Тогава променливата NEWDATE ще получи стойност "07/11/1996". Коефициентът на достоверност на тази стойност може да има следните стойности:

---------------------------------|Стойност | Описание | Пресмятания за CF | CF на | |на E. CFJO| | на NEWDAY+NEWYR |NEWDATE| ---------------------------------| M | Минимум |min(40, 60)=40 | ---------------------------------| P |Произведение|40*60/100=24 | ---------------------------------| A | Средно |(min(40, 60)+40*60/100)/2=32 | ---------------------------------| B | Баланс |40*60/100*(2 -max(40, 60)/100)=33. 6| 34 | ---------------------------------

Пример 2 Нека сега разгледаме следната поредица от команди за присвояване: LET NEWDAY = "07/11" CF 40 LET NEWYR = "/1996" CF 60 LET NEWDATE = NEWDAY + NEWYR CF 80

За разлика от предишния пример сега има само 80% увереност, че стойността на NEWDATE ще се определя от израза NEWDAY+NEWYR. NEWDATE ще получи същата стойност, както в предишния случай, но сега ще има по-нисък коефициент на достоверност. Намирането на този коефициент на достоверност включва следните допълнителни пресмятания, основани на стойността на променливата E. CFJO:
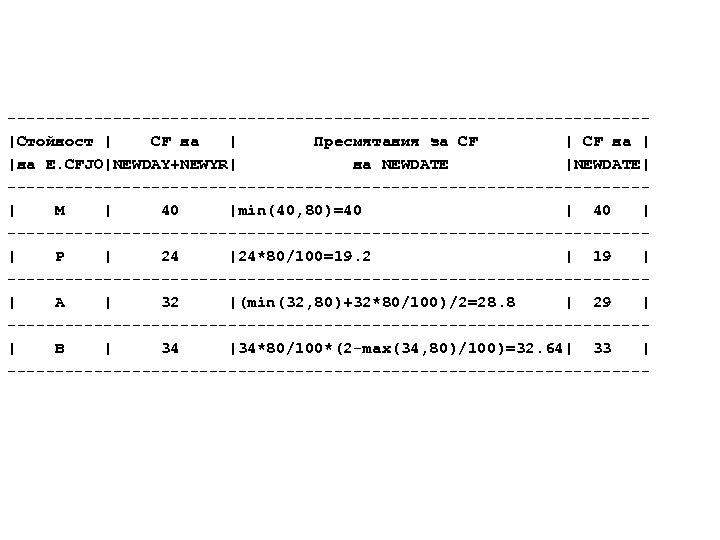
---------------------------------|Стойност | CF на | Пресмятания за CF | CF на | |на E. CFJO|NEWDAY+NEWYR| на NEWDATE |NEWDATE| ---------------------------------| M | 40 |min(40, 80)=40 | ---------------------------------| P | 24 |24*80/100=19. 2 | 19 | ---------------------------------| A | 32 |(min(32, 80)+32*80/100)/2=28. 8 | 29 | ---------------------------------| B | 34 |34*80/100*(2 -max(34, 80)/100)=32. 64| 33 | ----------------------------------

Коефициентът на достоверност на стойността на NEWDATE се нарича още съвместен коефициент на достоверност.

Числови изрази Всеки числов израз съдържа една или повече числови константи и/или променливи. Допустими числови оператори са: + (събиране), - (изваждане), * (умножение), / (деление), ** (степенуване), MOD (остатък по модул).

Коефициенти на достоверност на числови изрази Ако числовият израз включва само константи, без променливи, той има коефициент на достоверност 100. Ако числовият израз съдържа променливи, техните коефициенти на достоверност съвместно определят общия коефициент на достоверност на израза. И тук управляващата променлива на средата E. CFJO определя как се изчислява резултатният коефициент на достоверност. Пресмятанията се извършват по същия начин, както и при символните изрази.

Логически изрази Един логически израз обикновено включва едно или няколко сравнения. Всяко сравнение има стойност TRUE или FALSE. Сравненията могат да се комбинират в логически изрази с помощта на логическите (булевите) оператори NOT, AND (или &), OR, XOR. Логическите изрази имат стойност TRUE или FALSE.

Коефициенти на достоверност на логически изрази Ако едно сравнение включва само константи, то има коефициент на достоверност 100. Например, 15>6 е сравнение със стойност TRUE с коефициент на достоверност 100. Сравнението 6>15 има стойност FALSE с коефициент на достоверност 100.

Ако сравнението включва променливи и/или числови или символни изрази, в този случай техните коефициенти на достоверност съвместно допринасят за получаването на резултатния коефициент на достоверност на това сравнение. И тук променливата на средата E. CFJO определя как ще се пресмята резултатният коефициент на достоверност на изразите за сравнение.

Коефициентът на достоверност на даден съставен логически израз се определя по следния начин. Найнапред се пресмятат стойността (TRUE или FALSE) и коефициентът на достоверност на всички съставящи израза сравнения. Крайната стойност (TRUE или FALSE) на логическия израз се получава по обичайните правила. Коефициентът на достоверност на стойността на съставния логически израз зависи от:

- стойностите на съставящите го сравнения; - коефициентите на достоверност на съставящите го сравнения; - булевите оператори, които свързват съставящите логическия израз сравнения; - избраните методи за пресмятане на т. нар. съвместна и потвърждаваща достоверност, определени съответно от стойностите на променливите E. CFJO и E. CFCO.

Следват кратки сведения за начините за пресмятане на коефициента на достоверност на съставни логически изрази, съдържащи различните типове булеви оператори.

Нека предположим, че е даден логически израз, който включва две сравнения, свързани с оператор за конюнкция (AND или &). Ако и двата подизраза (двете сравнения) имат стойност TRUE, техните коефициенти на достоверност се комбинират съвместно за получаване на резултатния коефициент на достоверност. Методът за комбиниране на тези коефициенти на достоверност се определя от променливата E. CFJO.

Ако единият подизраз има стойност TRUЕ, а другият - стойност FALSE, то съставният израз има стойност FALSE с коефициент на достоверност, равен на коефициента на достоверност на подизраза със стойност FALSE. Ако и двата подизраза имат стойност FALSE, техните коефициенти на достоверност се комбинират по потвърждаващ начин, за да се получи резултатният коефициент на достоверност. Методът за комбиниране в потвърждаващ стил на тези коефициенти се определя от стойността на променливата на средата E. CFCO по следния начин:

-------------------------------| Стойност | Описание | Метод за пресмятане | | на E. CFCO | | | -------------------------------| M | Максимум | max(a, b) | -------------------------------| P | Вероятностна | a+b - a*b/100 | | | сума | | -------------------------------| A | Средно | (max(a, b) + (a+b-a*b/100))/2 | -------------------------------| B | Баланс | max(a, b)+min(a, b)*(1 -a/100)* | | (1 -b/100) | --------------------------------

От тези четири метода винаги методът на максимума дава най-нисък резултатен коефициент на достоверност, а методът на вероятностната сума - найвисок резултатен коефициент на достоверност.

Нека сега предположим, че е даден логически израз, който включва две сравнения (по-общо, два подизраза), свързани с оператор за дизюнкция (OR). Ако и двата подизраза имат стойност TRUE, то техните коефициенти на достоверност се комбинират в режим на потвърждаване, за да се получи резултатният коефициент на достоверност (използва се текущата стойност на променливата E. CFCO). Ако единият подизраз има стойност TRUE, а другият - стойност FALSE, резултатният коефициент на достоверност съвпада с този на подизраза със стойност TRUE. Ако и двата подизраза имат стойност FALSE, техните коефициенти на достоверност се комбинират по съвместно влияещ си начин, като за целта се използва текущата стойност на променливата E. CFJO.

Ако оператор XOR свързва две сравнения (два подизраза), техните коефициенти на достоверност съвместно допринасят за получаването на резултатната достоверност. В този случай се използва текущата стойност на променливата на средата E. CFJO. Тъй като операторът за логическо отрицание NOT е едноаргументен, той не изисква комбиниране на коефициенти на достоверност.

Изрази с неопределена стойност Ако един израз съдържа неопределена променлива, то неговата стойност не може да бъде изчислена. Например, след изпълнението на поредицата от команди: LET A = UNKNOWN LET B = 5 LET C = A+B променливата C е неопределена, тъй като стойността на израза A+B е неопределена.

Размити изрази Един израз може да съдържа една или няколко размити променливи. Когато такъв израз се оценява, той може да получи множество от стойности, всяка от които ще има свой собствен коефициент на достоверност. Множеството от стойностите на размития израз се получава чрез комбиниране на възможните стойности на участващите променливи.

При това, когато две различни стойности на дадена размита променлива водят до получаване на един и същ резултат при оценяването на съответния израз, GURU определя коефициента на достоверност на този резултат (на тази стойност на израза), използвайки метода на потвърждаването, зададен като стойност на променливата на средата E. CFCO.

Същата философия се използва и за увеличаване на коефициента на достоверност на вече съществуваща стойност на дадена размита променлива с помощта на командата +=. И в този случай се използва методът за получаване на потвърждаващата достоверност, определен от променливата E. CFCO.

При намаляване на достоверността на вече съществуваща стойност на дадена размита променлива с помощта на командата -= се използва методът за получаване на съвместната достоверност, определен от променливата E. CFJO (за целта се използват съществуващият коефициент на достoверност и допълнението до 100 на новозададения коефициент на достоверност).
412bad212052c013a59227ca86767669.ppt