РАБОТА КОГЕЗИИ, Wк 1 м 2 1 Wк

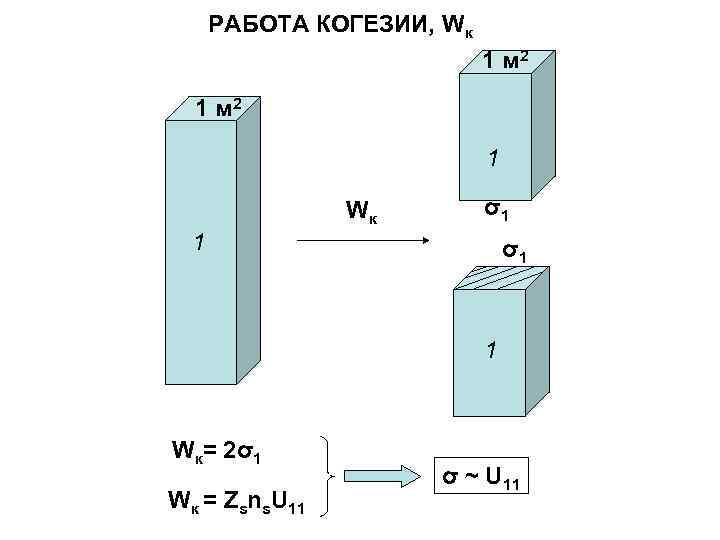
РАБОТА КОГЕЗИИ, Wк 1 м 2 1 Wк σ1 1 Wк= 2σ1 Wк = Zsns. U 11 σ ~ U 11

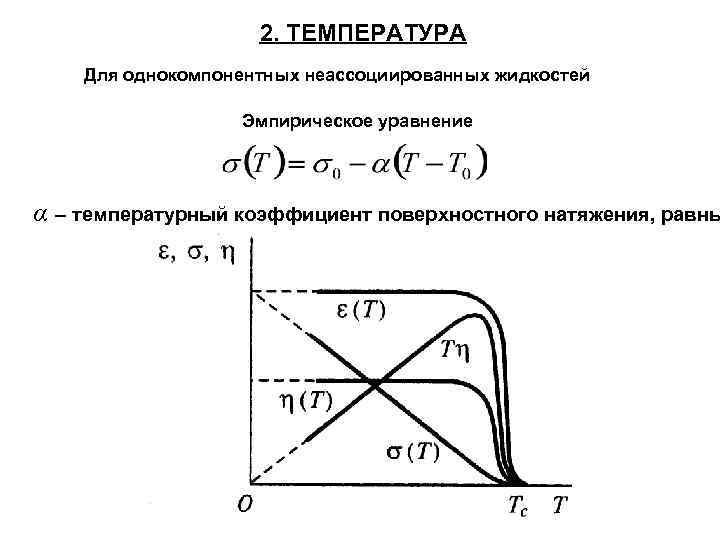
2. ТЕМПЕРАТУРА Для однокомпонентных неассоциированных жидкостей Эмпирическое уравнение α – температурный коэффициент поверхностного натяжения, равны

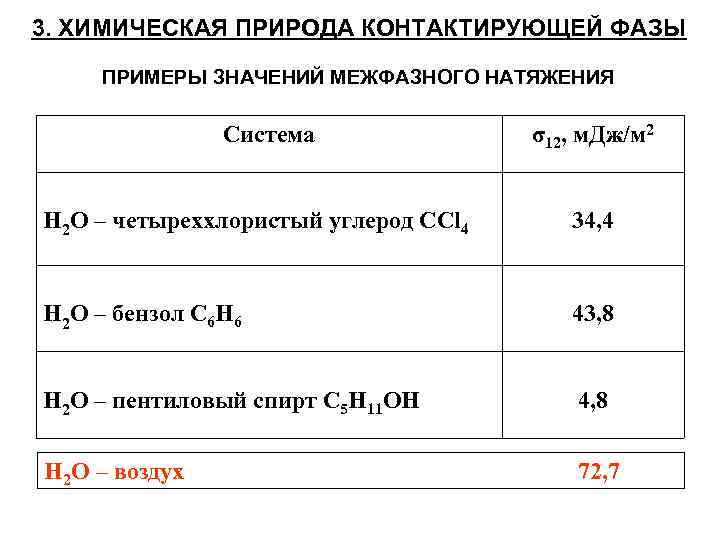
3. ХИМИЧЕСКАЯ ПРИРОДА КОНТАКТИРУЮЩЕЙ ФАЗЫ ПРИМЕРЫ ЗНАЧЕНИЙ МЕЖФАЗНОГО НАТЯЖЕНИЯ Система σ12, м. Дж/м 2 Н 2 О – четыреххлористый углерод СCl 4 34, 4 Н 2 О – бензол C 6 H 6 43, 8 Н 2 О – пентиловый спирт C 5 H 11 OH 4, 8 Н 2 О – воздух 72, 7

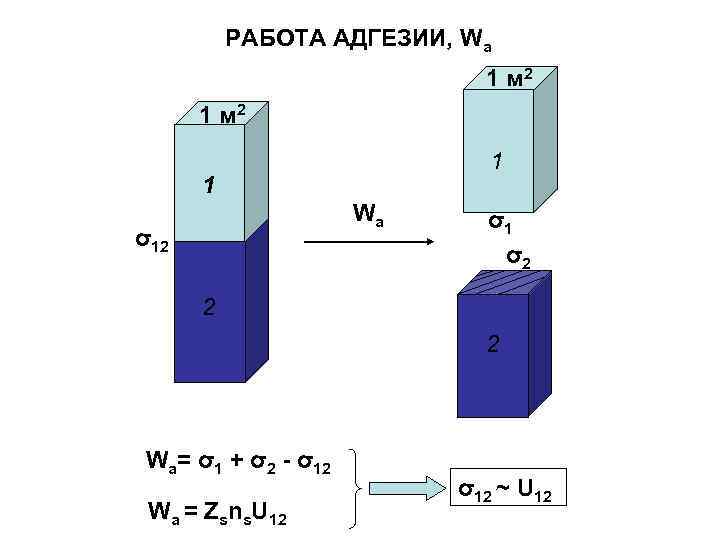
РАБОТА АДГЕЗИИ, Wa 1 м 2 1 1 Wа σ12 σ1 σ2 2 2 Wа= σ1 + σ2 - σ12 Wа = Zsns. U 12 σ12 ~ U 12

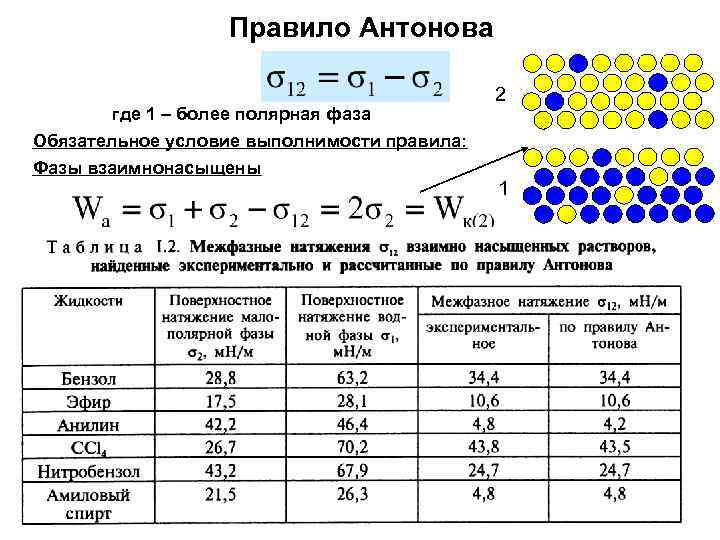
Правило Антонова где 1 – более полярная фаза Обязательное условие выполнимости правила: Фазы взаимнонасыщены 2 1

Лекция № 2 ЯВЛЕНИЕ СМАЧИВАНИЯ КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ

СМАЧИВАНИЕ – распространенное физико-химическое явление в многофазных системах, где взаимодействует жидкость с поверхностью твердых тел в газе или другой жидкости

В зависимости от числа фаз, участвующих в смачивании, различают два случая: 1. Иммерсионное смачивание (при полном погружении твердого тела в жидкость), в котором участвуют две фазы – жидкость и твердое тело. 2. Контактное смачивание, в котором наряду с жидкостью и твердым телом участвует третья фаза – газ или другая жидкость

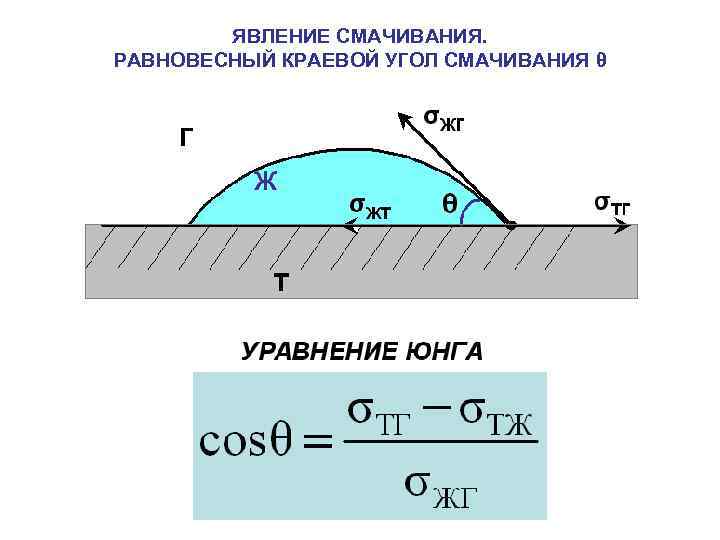
ЯВЛЕНИЕ СМАЧИВАНИЯ. РАВНОВЕСНЫЙ КРАЕВОЙ УГОЛ СМАЧИВАНИЯ θ

ЭНЕРГЕТИЧЕСКИЙ ВЫВОД УРАВНЕНИЯ ЮНГА основан на изменении свободной поверхностной энергии системы на единицу длины линии трехфазного контакта при смещении поверхности жидкости вниз на dl Поверхность жидкости вблизи вертикальной твердой пластины

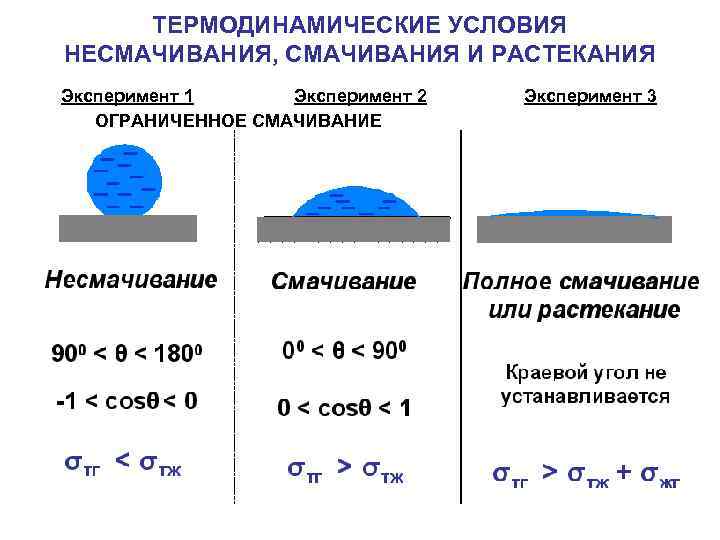
ТЕРМОДИНАМИЧЕСКИЕ УСЛОВИЯ НЕСМАЧИВАНИЯ, СМАЧИВАНИЯ И РАСТЕКАНИЯ Эксперимент 1 Эксперимент 2 ОГРАНИЧЕННОЕ СМАЧИВАНИЕ Эксперимент 3

СВЯЗЬ КРАЕВОГО УГЛА С РАБОТОЙ АДГЕЗИИ И КОГЕЗИИ

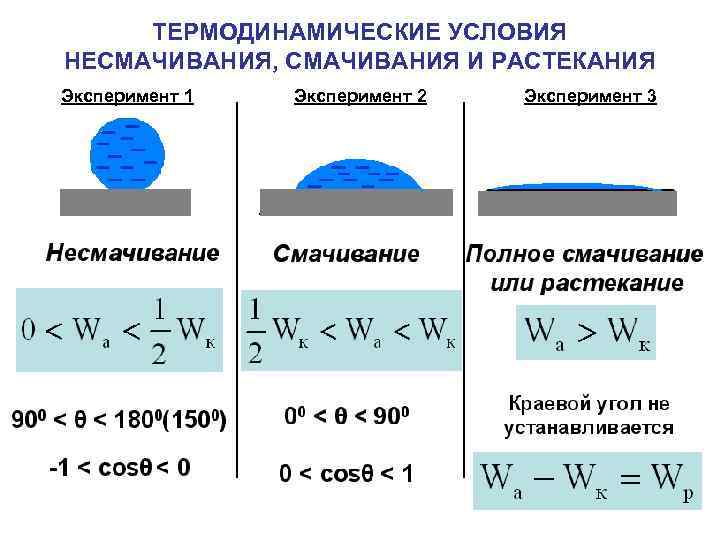
ТЕРМОДИНАМИЧЕСКИЕ УСЛОВИЯ НЕСМАЧИВАНИЯ, СМАЧИВАНИЯ И РАСТЕКАНИЯ Эксперимент 1 Эксперимент 2 Эксперимент 3

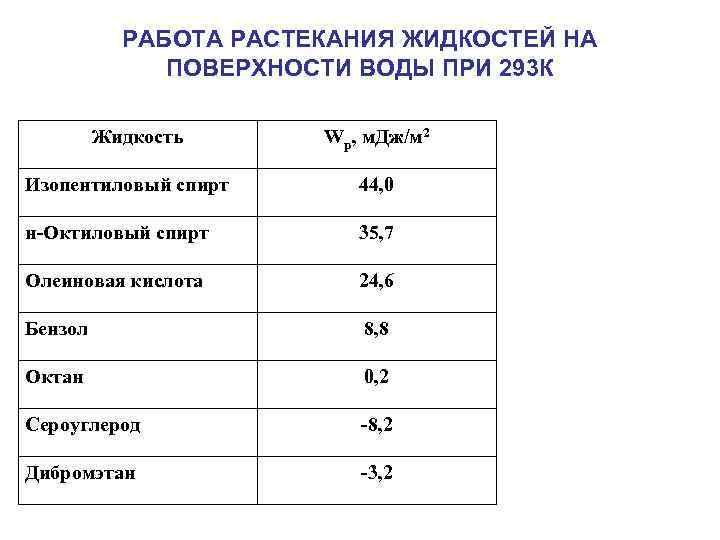
РАБОТА РАСТЕКАНИЯ ЖИДКОСТЕЙ НА ПОВЕРХНОСТИ ВОДЫ ПРИ 293 К Жидкость Wр, м. Дж/м 2 Изопентиловый спирт 44, 0 н-Октиловый спирт 35, 7 Олеиновая кислота 24, 6 Бензол 8, 8 Октан 0, 2 Сероуглерод -8, 2 Дибромэтан -3, 2

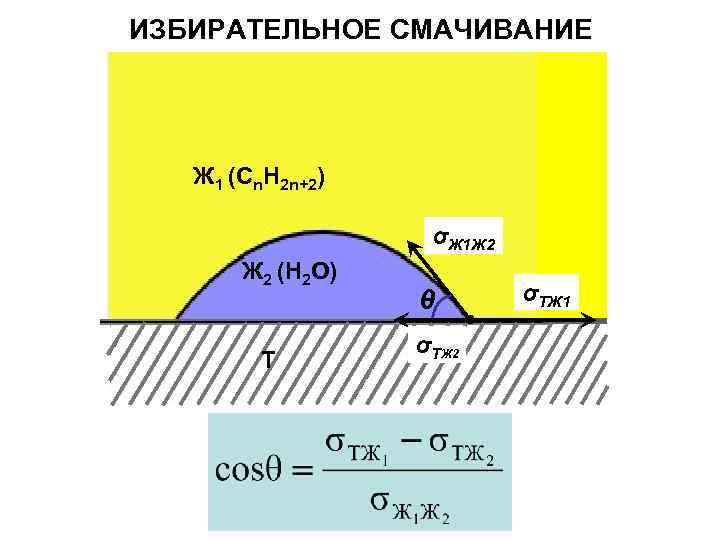
ИЗБИРАТЕЛЬНОЕ СМАЧИВАНИЕ Ж 1 (Cn. H 2 n+2) σЖ 1 Ж 2 (H 2 O) Т θ σТЖ 2 σТЖ 1

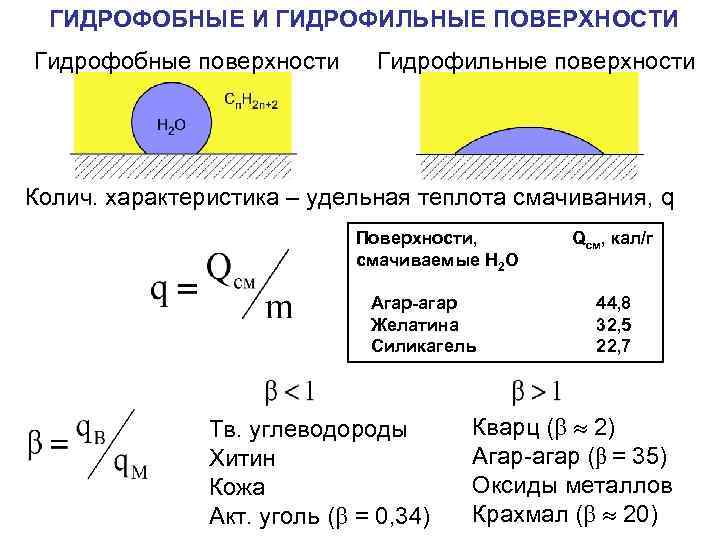
ГИДРОФОБНЫЕ И ГИДРОФИЛЬНЫЕ ПОВЕРХНОСТИ Гидрофобные поверхности Гидрофильные поверхности Колич. характеристика – удельная теплота смачивания, q Поверхности, смачиваемые H 2 O Агар-агар Желатина Силикагель Тв. углеводороды Хитин Кожа Акт. уголь ( = 0, 34) Qсм, кал/г 44, 8 32, 5 22, 7 Кварц ( 2) Агар-агар (β = 35) Оксиды металлов Крахмал ( 20)

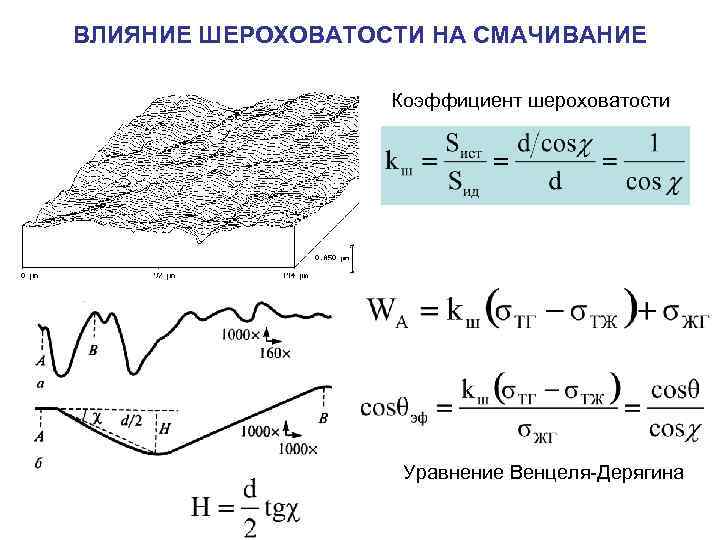
ВЛИЯНИЕ ШЕРОХОВАТОСТИ НА СМАЧИВАНИЕ Коэффициент шероховатости Уравнение Венцеля-Дерягина

ЭФФЕКТ ЛОТОСА

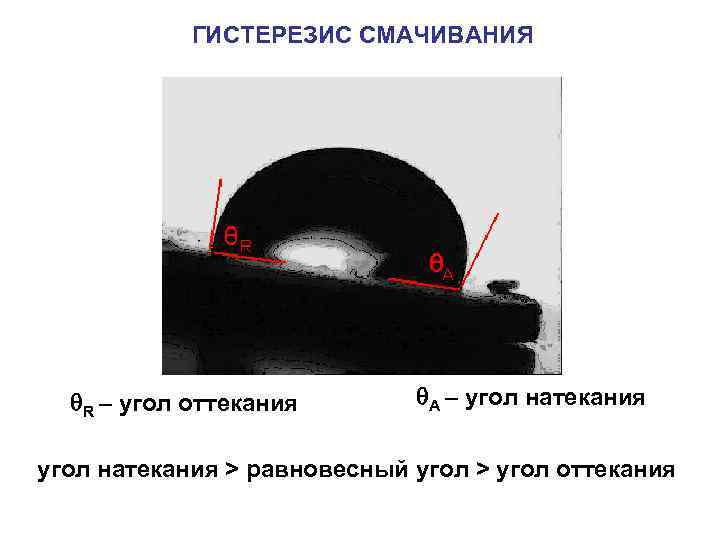
ГИСТЕРЕЗИС СМАЧИВАНИЯ R – угол оттекания А – угол натекания > равновесный угол > угол оттекания

Капиллярные явления

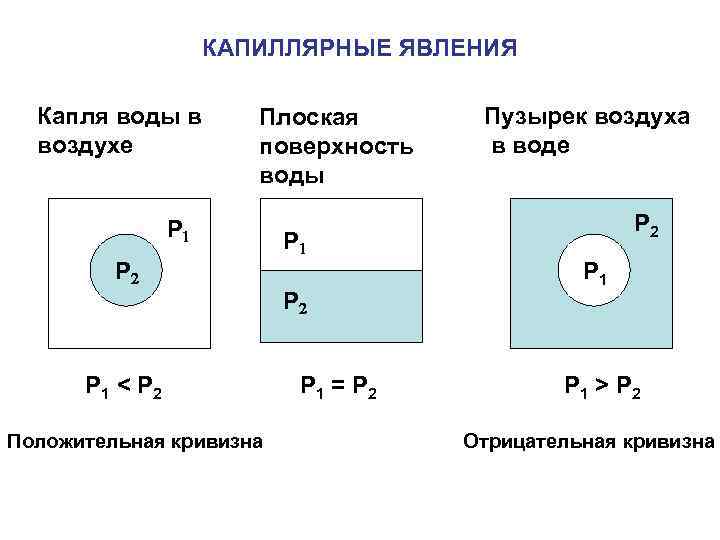
КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ Капля воды в воздухе Плоская поверхность воды P 1 P 2 P 1 < P 2 Положительная кривизна P 1 P 2 P 1 = P 2 Пузырек воздуха в воде P 2 P 1 > P 2 Отрицательная кривизна

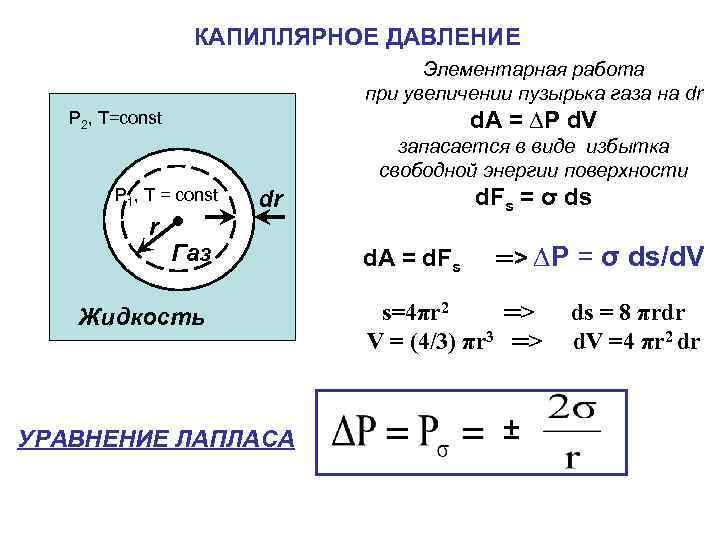
КАПИЛЛЯРНОЕ ДАВЛЕНИЕ Элементарная работа при увеличении пузырька газа на dr d. A = ∆P d. V P 2, T=const запасается в виде избытка свободной энергии поверхности Р 1, T = const r d. Fs = σ ds dr Газ Жидкость УРАВНЕНИЕ ЛАПЛАСА d. A = d. Fs ═> ∆P = σ ds/d. V s=4πr 2 ═> V = (4/3) πr 3 ═> ± ds = 8 πrdr d. V =4 πr 2 dr

УРАВНЕНИЕ ЛАПЛАСА В общем виде r 1 и r 2 – главные радиусы кривизны

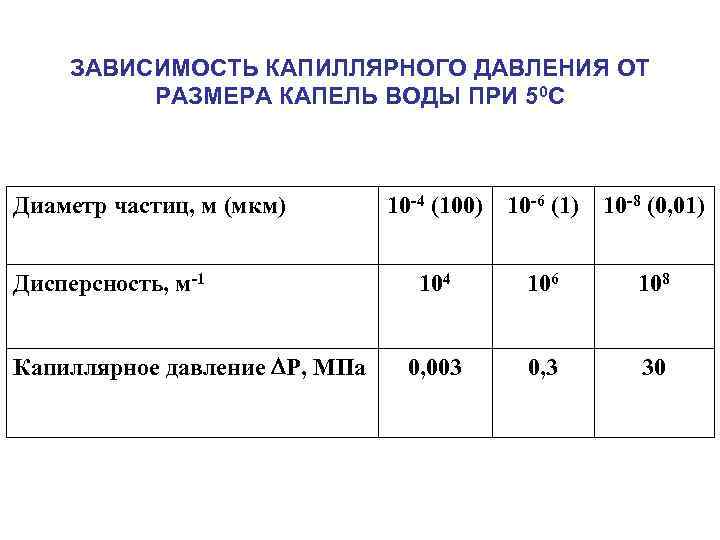
ЗАВИСИМОСТЬ КАПИЛЛЯРНОГО ДАВЛЕНИЯ ОТ РАЗМЕРА КАПЕЛЬ ВОДЫ ПРИ 50 С Диаметр частиц, м (мкм) Дисперсность, м-1 Капиллярное давление P, МПа 10 -4 (100) 10 -6 (1) 10 -8 (0, 01) 104 106 108 0, 003 0, 3 30

ПОДНЯТИЕ ОКРАШЕННОЙ ВОДЫ В СТЕКЛЯННОМ КАПИЛЛЯРЕ

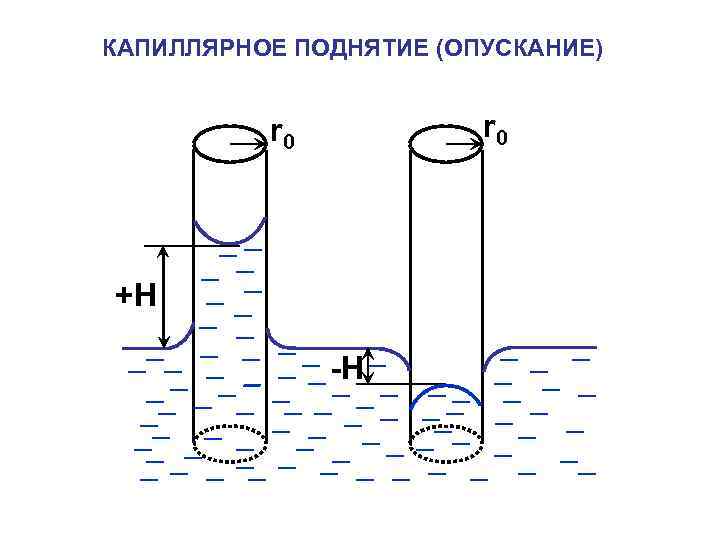
КАПИЛЛЯРНОЕ ПОДНЯТИЕ (ОПУСКАНИЕ) r 0 +H -H

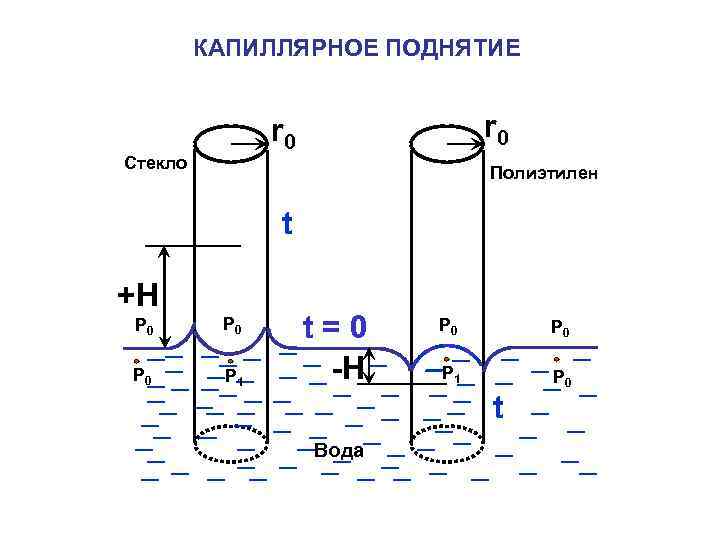
КАПИЛЛЯРНОЕ ПОДНЯТИЕ r 0 Стекло Полиэтилен t +H P 0 P 0 P 1 t=0 -H P 0 P 1 P 0 t Вода

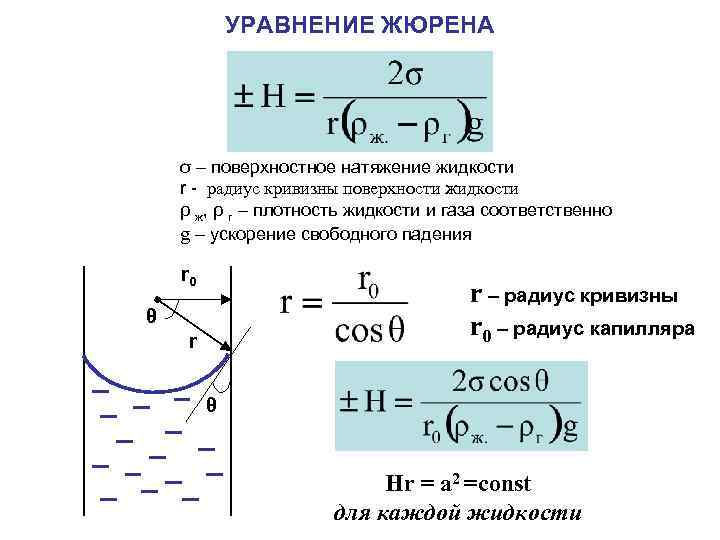
УРАВНЕНИЕ ЖЮРЕНА σ – поверхностное натяжение жидкости r - радиус кривизны поверхности жидкости ρ ж, ρ г – плотность жидкости и газа соответственно g – ускорение свободного падения r 0 r – радиус кривизны r 0 – радиус капилляра θ r θ Hr = a 2 =const для каждой жидкости

ВЫСОТА ПОДНЯТИЯ ВОДЫ В СТЕКЛЯННОМ КАПИЛЛЯРЕ ПРИ УСЛОВИИ ПОЛНОГО СМАЧИВАНИЯ r 0 1 см 1 мкм 1 нм Н 1, 5 мм 1, 5 см 15 км

КАПИЛЛЯРНАЯ СТЯГИВАЮЩАЯ СИЛА

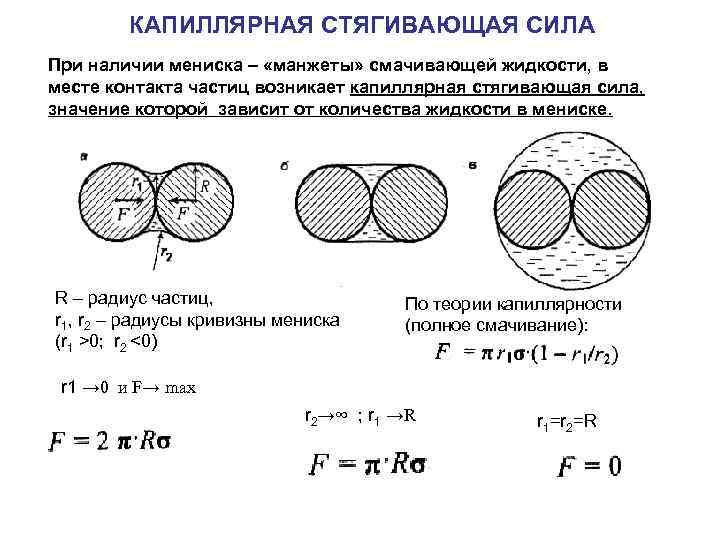
КАПИЛЛЯРНАЯ СТЯГИВАЮЩАЯ СИЛА При наличии мениска – «манжеты» смачивающей жидкости, в месте контакта частиц возникает капиллярная стягивающая сила, значение которой зависит от количества жидкости в мениске. R – радиус частиц, r 1, r 2 – радиусы кривизны мениска (r 1 >0; r 2 <0) По теории капиллярности (полное смачивание): r 1 → 0 и F→ max r 2→∞ ; r 1 →R r 1=r 2=R

ЗАКОН ТОМПСОНА (КЕЛЬВИНА) – зависимость давления насыщенного пара от радиуса кривизны P 0 - давление насыщенного пара над плоской поверхностью жидкости σ - поверхностное натяжение жидкости Vm- молярный объем жидкости r - радиус кривизны R - универсальная газовая постоянная T - температура

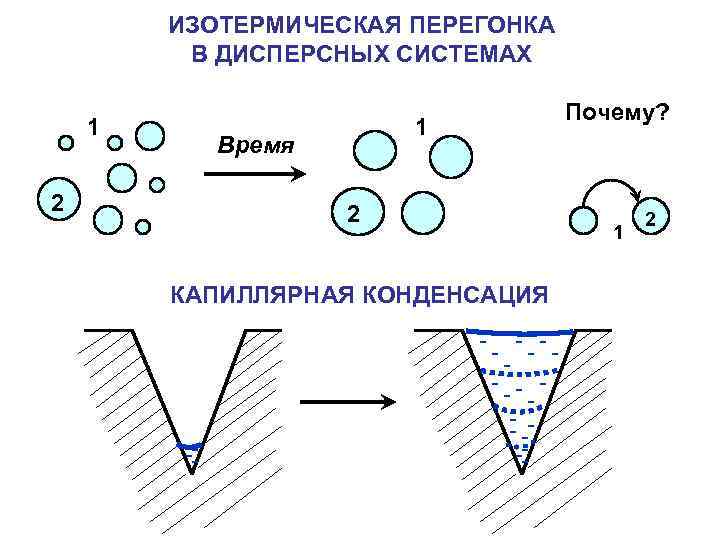
ИЗОТЕРМИЧЕСКАЯ ПЕРЕГОНКА В ДИСПЕРСНЫХ СИСТЕМАХ 1 2 1 Время 2 КАПИЛЛЯРНАЯ КОНДЕНСАЦИЯ Почему? 1 2

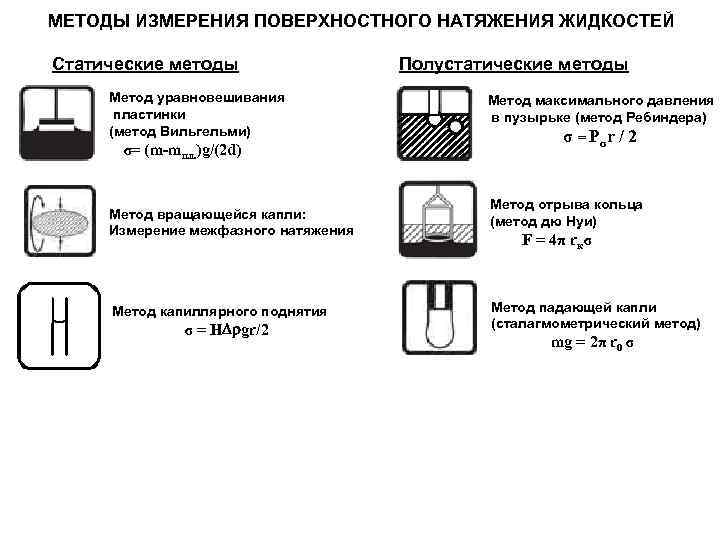
МЕТОДЫ ИЗМЕРЕНИЯ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТЕЙ Статические методы Метод уравновешивания пластинки (метод Вильгельми) σ= (m-mпл. )g/(2 d) Метод вращающейся капли: Измерение межфазного натяжения Метод капиллярного поднятия σ = H gr/2 Полустатические методы Метод максимального давления в пузырьке (метод Ребиндера) σ = Pσ r / 2 Метод отрыва кольца (метод дю Нуи) F = 4π rкσ Метод падающей капли (сталагмометрический метод) mg = 2π r 0 σ