Работа и энергия лекция 3 Работа

Работа и энергия лекция 3

§§ Работа и мощность Работой силы на перемещении называется произведение величины проекции силы на перемещение и величины перемещения где α – угол между и . размерность: [A] = 1 Дж (Джоуль) = 1 Н∙м 02

В общем случае траектории, когда м. т. проходит путь конечной длины называется предел криволинейным интегралом Если на м. т. действует несколько сил, то работа результирующей силы 03

Мощность – величина, показывающая, какую работу совершает сила в единицу времени – средняя мощность – мгновенная мощность – связь мощности и работы 04

с другой стороны: следовательно Единица измерения мощности: [N] = 1 Вт (Ватт) = 1 Дж/с 05

§§ Энергия Физическая величина, характеризующая способность м. т. (или с. м. т. ) совершать работу, называется энергией действует Пусть на м. т. сила , перемещая ее из положения 1 в 2 06

поскольку и, следовательно Величина называется кинетической энергией 07

Теорема об изменении кин. энергии Работа всех сил (внешних и внутренних) равна приращению кин. энергии системы Замечание: в СТО – масса покоя частицы – энергия покоя частицы – масса движения Кин. энергия: при получаем 08

§§ Работа постоянной силы Вычислим работу силы тяжести при переходе из 1 в 2 1) Вдоль отрезка где 09

2) Вдоль произвольного пути Разобьем весь путь на малые участки – работа на i-м участке т. е. работа не зависит от формы пути, а определяется только начальным и конечным положениями. 10

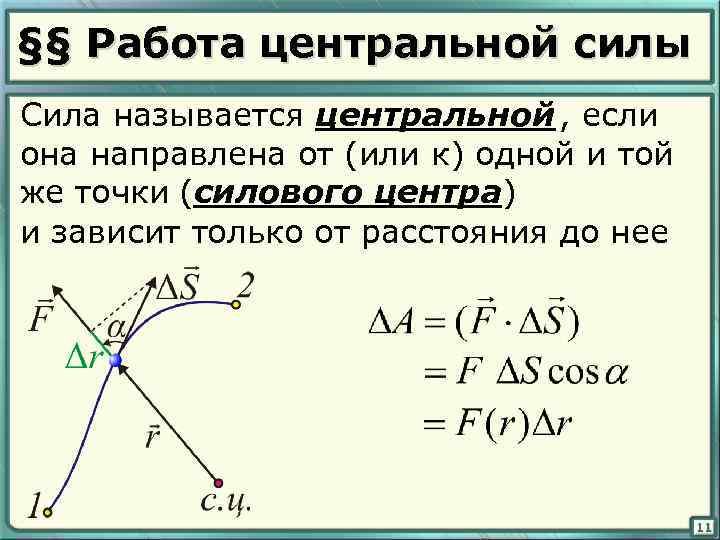
§§ Работа центральной силы Сила называется центральной , если она направлена от (или к) одной и той же точки (силового центра) и зависит только от расстояния до нее 11

т. е. работа центральной силы не зависит от формы траектории, а определяется только начальным и конечным положением 12

§§ Консервативные силы Сила, работа которой не зависит от формы пути перехода из произвольного начального положения в произвольное конечное, а определяется лишь начальным и конечным положением, называется консервативной Работа такой силы по любому замкнутому пути равна нулю 13

К неконсервативным силам относят диссипативные силы [dissipate (англ) – рассеивать, расточать] (силы трения и сопротивления), у которых работа на любом перемещении отрицательна и гироскопические силы – (например, сила Лоренца, Кориолиса) это те силы, которые зависят от скорости тела (м. т. ) и всегда ей перпендикулярны. Работа гироскопических сил на любых перемещениях равна нулю 14

Сила Кориолиса: 1) разгоняет платформу при движении человека к центру 2) объясняет прецессию гироскопа 3) из-за наличия этой силы подмываются восточные берега у рек, текущих на север 4) объясняет наличие преимущественных ветров (пассатов) 15

§§ Потенциальная энергия Для системы, где действуют только консервативные и гироскопические силы, можно ввести понятие потенциальной энергии Произвольное положение такой системы примем за нулевое. Работа, совершаемая консервативными силами при переходе системы в нулевое положение, называется потенциальной энергией. 16

Свойства: 1) она является функцией только координат (конфигурации) 2) определена с точностью до произвольной постоянной. (т. е. имеет смысл говорить только о разности потенциальных энергий) 3) не зависит от выбора ИСО 17

Рассмотрим переход системы из положения 1 в положение 2 т. е. работа консервативных сил равна убыли потенциальной энергии системы 18

§§ Закон сохранения энергии Вычислим работу A 12 Приравнивая, получаем: Сумма кинетической и потенциальной энергии называется полной энергией это энергия движения и взаимодействия 19

Закон сохранения энергии в механике: В системе, где действуют только консервативные и гироскопические силы, полная энергия остается неизменной. Могут происходить лишь превращения кинетической энергии в потенциальную, и обратно. 20

Если в системе действуют диссипативные силы, тогда: получаем полная энергия уменьшается В самом общем случае – работа всех сил, не учитываемых в выражении для потенциальной энергии. 21