Query Processing Exercise Session 1 1 How

Query Processing Exercise Session 1 1

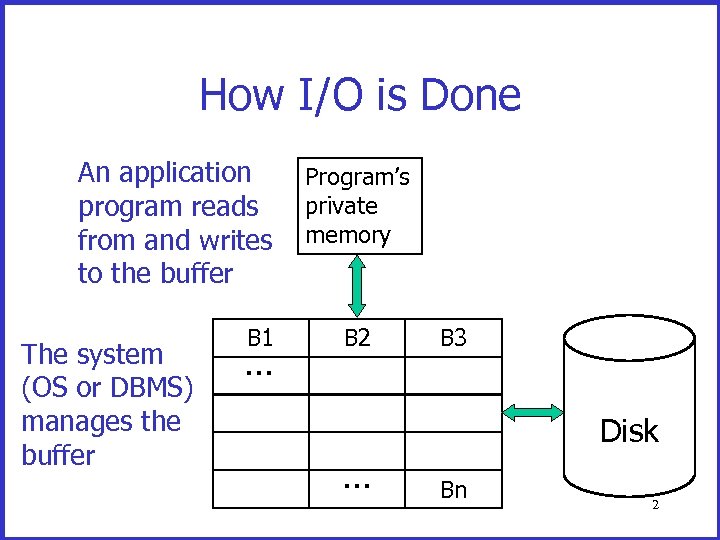How I/O is Done An application program reads from and writes to the buffer The system (OS or DBMS) manages the buffer B 1 … Program’s private memory B 2 B 3 Disk … Bn 2

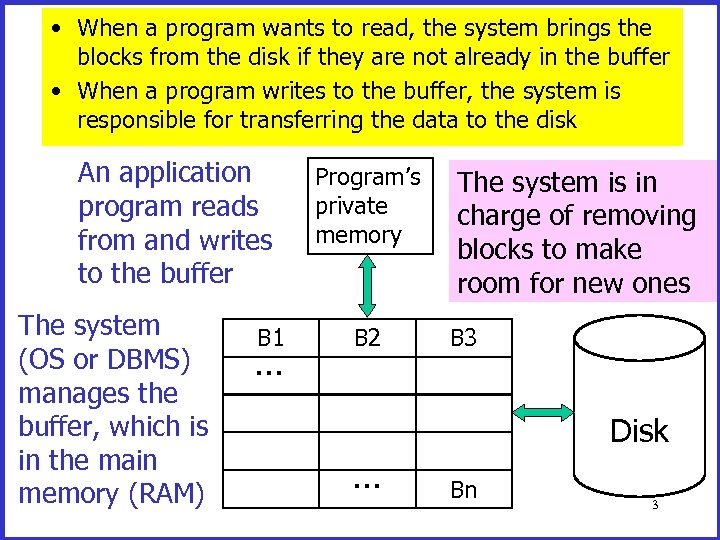• When a program wants to read, the system brings the blocks from the disk if they are not already in the buffer • When a program writes to the buffer, the system is responsible for transferring the data to the disk How I/O is Done An application program reads from and writes to the buffer The system (OS or DBMS) manages the buffer, which is in the main memory (RAM) B 1 … Program’s private memory B 2 The system is in charge of removing blocks to make room for new ones B 3 Disk … Bn 3

Note that • An application program is not aware that there are blocks and buffers • It performs I/O operations directly on records, almost as if those records are always in main memory 4

Replacement Policies • When the buffer is full, which block should be removed? – The one that will be needed again only a long time from now • OS usually implements a policy of LRU (least recently used) • What if all the blocks in the buffer are still needed by the programs running now? 5

Why LRU is not Good for DBMS • An example: – The size of the buffer is n-1 blocks – We need to read several times a sequential file that has n blocks • In this case, MRU (most recently used) is the best policy (for deciding which block to remove) – Same when reading nodes of a B+tree 6

How to Use a Buffer Efficiently Problem: Have a File » Sequence of Blocks B 1, B 2 . . . Have a Program » Process B 1 » Process B 2 » Process B 3 7

Single-Buffer Solution (1) (2) (3) (4) Read B 1 Buffer Process Data in Memory Read B 2 Buffer Process Data in Memory. . . 8

Total Time (not just I/O) Say P = time to process 1 block R = time to read 1 block from disk n = # blocks Single-buffer time = n(P+R) 9

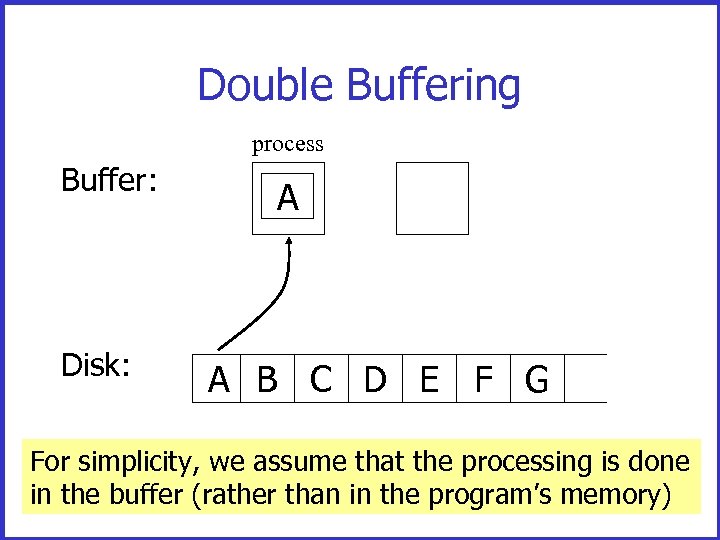Double Buffering process Buffer: Disk: A A B C D E F G For simplicity, we assume that the processing is done in the buffer (rather than in the program’s memory) 10

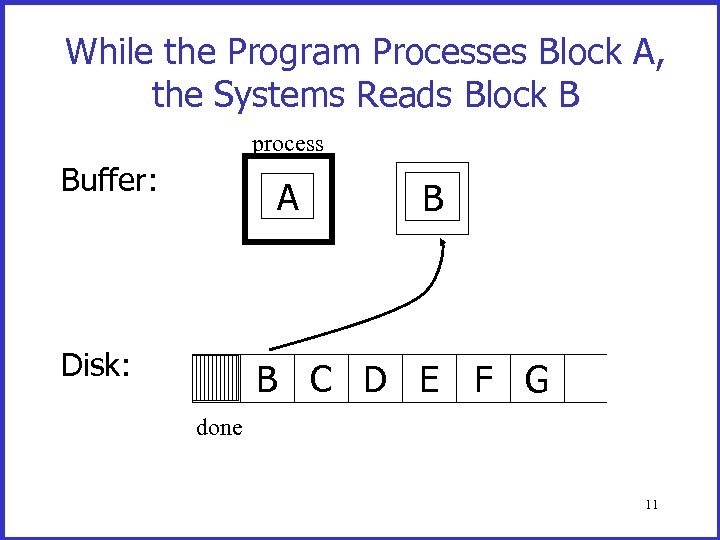While the Program Processes Block A, the Systems Reads Block B process Buffer: Disk: A B C D E F G done 11

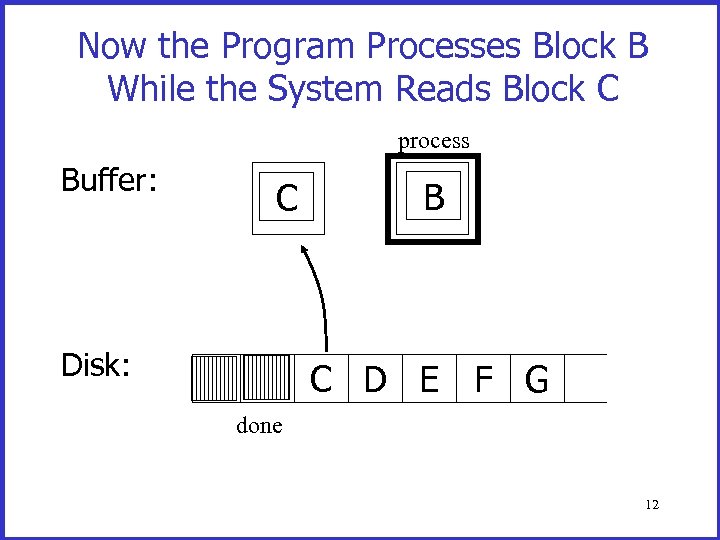Now the Program Processes Block B While the System Reads Block C process Buffer: Disk: A C B A B C D E F G done 12

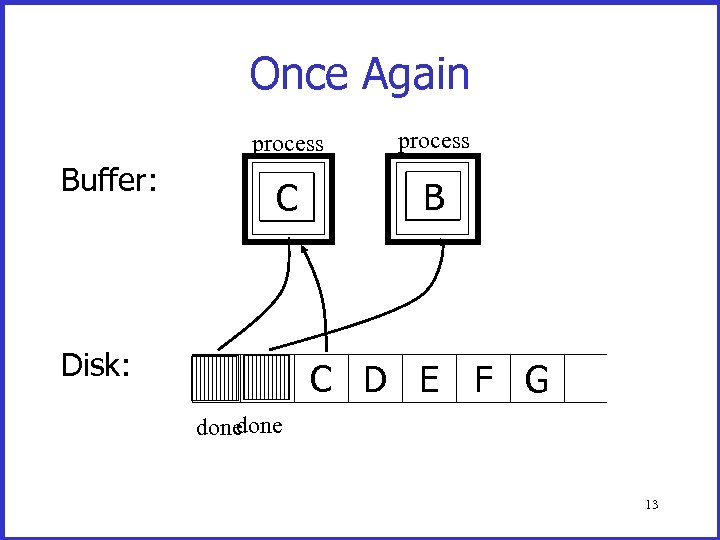Once Again process Buffer: Disk: process C A B C D E F G done 13

Total Time Assuming P R P = Time to process 1 block R = Time to read 1 block n = # blocks • What is the total time? – Single buffering time – Double buffering time = n(R+P) = • The CPU time hardly affects the total length of the computation • It is correct to count just the I/O operations when analyzing running time 14

The Actual Difference • The actual difference between single and double buffering is much worse than n(R+P) – (n. R+P), why? • These are actually two different R – Because double buffering enables reading the file sequentially, whereas single buffering is even worse than random reading since the latency is almost a full revolution 15

Questions • Is double buffering useful also when writing to the disk? • How do you activate double buffering? • Suppose your program is a CPU cruncher, that is, P R – Compute the total time for single and double buffering when P R • Does double buffering help? 16

Comments • “Double buffering” is not limited to using just a buffer of two blocks – An application program processes k blocks in main memory while the system reads the next k blocks • Read-ahead buffering – When an application wants to read one block, the system reads several more blocks sequentially in anticipation that the application will need them – This is just one example of double buffering 17

Best Case of Joining 2 Relations Relation R has BR blocks Relation S has BS block The size of the result is C blocks The best possible I/O cost is BR + BS + C • How much memory is needed to achieve this cost? • • 18

Selection Do the answers depend on the total number of blocks? • ID is a unique key, so what is the cost of doing the selection ID=102? • Name is not a unique key, there are 1, 000 records with the name “levy”, and a block can store 50 records – What is the cost of the selection Name=“levy”? • Depends on whether the records are clustered on Name, that is, whether all the records with the same name are physically close to each other on the disk – If sorted then clustered Records cannot be clustered on two different fields! 19 (unless one is a unique key)

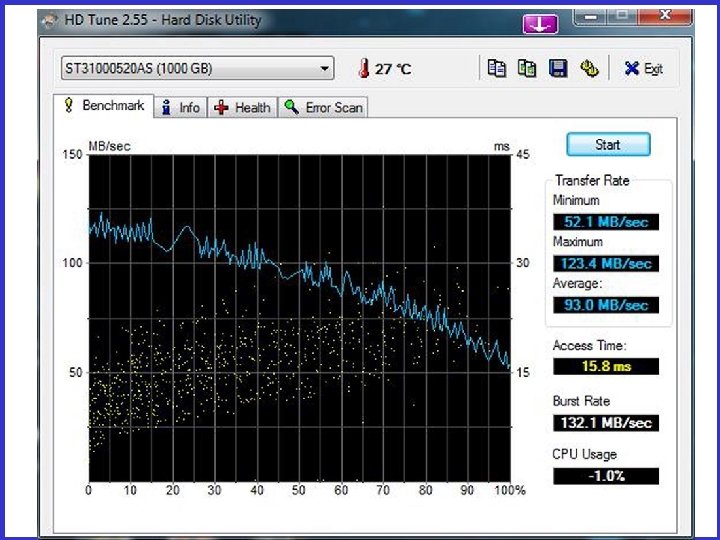
Zone Bit Recording • All sectors have the same capacity (typically 512 bytes) • All tracks used to have the same number of sectors, but not anymore – why? • Sustained transfer rate OD (outer diameter) is higher • This rate goes down as the heads move toward the center – Use a software tool to measure the sustained transfer rate of your disks 20

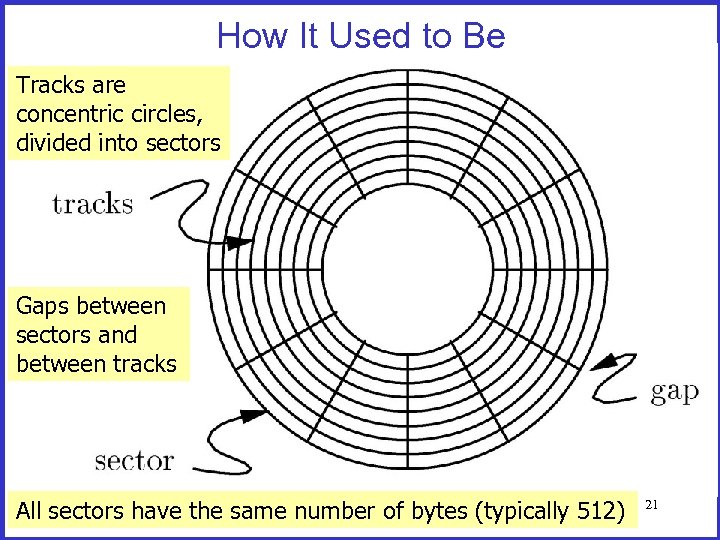How It Used to Be Tracks are concentric circles, divided into sectors Gaps between sectors and between tracks All sectors have the same number of bytes (typically 512) 21

Zone Bit Recording 22

23

Physical Addresses are Just “Logical” • The physical address of a block consists of – Device ID – Cylinder # – Surface # (i. e. , track number) – Sector # Same number of sectors in every track • Due to zone bit recording (and other reasons), the physical addresses do not reflect the true geometry of the disk 24

The Five-Minute Rule • The Five-minute Rule for Trading Memory for Disc Accesses Jim Gray & Franco Putzolu, 1987 • The Five Minute Rule, Ten Years Later Goetz Graefe & Jim Gray, 1997 • The five-minute rule 20 years later (and how flash memory changes the rules) Goetz Graefe, 2009 (originally 2007) 25

IOPS • IOPS = I/O Operations Per Second – Currently, IOPS is in the range 100 – 200 • D = price of a disk • I = # of IOPS • A block has to be brought into memory every X seconds • The (proportional) cost is D/(XI) 26

An Alternative • Keep the block in memory all the time • M = the cost of memory (RAM) for 1 block (varies with the size of the block) • Break-even point is when equality holds, that is, M = D/(XI) and hence X= D IM 27

The New Rule • Cost of 1 IOP is about $1 • Cost of 1 MB RAM is about $0. 05 – The # of 4 KB blocks in 1 MB is 256 • Hence, X is about 90 minutes – Used to be about 5 minutes in 1987 & 1997 • Buy RAM for each block you need at least every 90 minutes 28

Not Only A Matter of Cost • The poor IOPS performance of hard disks is a bottleneck of I/O-intensive systems • The solution is solid-state drives (SSD) – http: //www. theregister. co. uk/2009/09/23/i nsane_ssd_performance/ 29

Disk Arrays • RAIDs (various flavors) • Block Striping • Mirrored logically one disk 30

RAID Tutorial • http: //www. acnc. com/04_01_00. html 31

On-Disk Cache P. . . M C . . . cache 32

Summary of Optimizations • Disk-Scheduling Algorithms – e. g. , elevator algorithm • Larger Blocks (8 KB nowadays) and larger buffers – As the price of RAM drops, blocks and buffers get bigger • Read-Ahead Buffering – this is useful if – The system knows in advance the blocks that will be needed shortly, or – The systems guesses correctly that the following N contiguous blocks are going to be needed • RAID • On-Disk Cache 33

A Bit More on Bytes • What does burst rate mean? • Gibibytes vs. Gigabytes – gibibytes = gigabinary bytes • Memory is measured in gibibytes whereas the capacity of disks is given in gigabytes • 1 MB = K K, 1 GB = K K K • K = 1024 for RAM but only 1000 for disks 34

Relational Operations on Bags • What are the definitions of the five basic operators when they are applied under the bag semantics, that is, relations may have duplicates? • When can we push selection and projection through join? 35

Pushing Selections and Projections Does it work also for bags? • Repeatedly split each selection with ⋀ using the equivalence C 1⋀C 2(E) ≡ C 1( C 2(E)) • Repeatedly do the following: – Push selections through projections – Push selections into every operand of a natural join if possible (i. e. , if the operand contains all the attributes of the selection) • After each selection and each join, do projection that leaves only attributes that are needed either for later selections and joins, or for the final result 36

The Duplicate-Elimination Operator • is the operation of duplicate elimination • The result of (R) is obtained from R by removing duplicates • Through which operations can we push ? 37