45558537ad125e8a01f09c138d2d7093.ppt
- Количество слайдов: 18

Quarkonia Correlators above Deconfinement Ágnes Mócsy FIAS & ITP, Frankfurt * Why interested in quarkonia correlators * Calculating correlators * Charm and bottom results - compare to lattice * What have we learned so far in collaboration w/ Péter Petreczky

Why interested in quarkonia * Screening prevents J/ binding above Tc color screening length < size of resonance Matsui, Satz ‘ 86 * Sequential dissolution higher excitations melt earlier Karsch, Mehr, Satz ‘ 88 * J/ disappears at 1. 1 Tc in potential model Digal, Petreczky, Satz ‘ 01 * From the lattice J/ melts abruptly at 1. 6 Tc < T < 1. 9 Tc Umeda; Asakawa, Hatsuda ‘ 04 J/ , c survive ~ 1. 5 Tc & gradually melt by ~ 3 Tc + masses don’t change c 0, c 1 dissolve ~ 1. 1 Tc Datta, Karsch, Petreczky, Wetzorke ‘ 04 b unchanged ~ 2 Tc & b at ~ 1. 15 Tc Petrov, Petreczky QM 05 Can quarkonia exist as resonances above deconfinement ? Ágnes Mócsy, Frankfurt

Euclidean correlator measured on the lattice Spectral function reconstructed on lattice w/ MEM OR model input deviation from 1 suggests medium effects Ágnes Mócsy, Frankfurt

Why the c and J/ behave different? c - significant deviations ~ 3 Tc J/ - deviations ~ 1. 5 Tc Datta, Karsch, Petreczky, Wetzorke ‘ 04 And why is the b different? - drastic change ~ 1. 15 Tc although same size as c Petrov, Petreczky QM 05 Ágnes Mócsy, Frankfurt

Calculating correlators resonances perturbative continuum threshold bound state mass decay constant Mi = 2 m + Ei Ei binding energy radial wave function in origin from What potential V(r) ? Ágnes Mócsy, Frankfurt
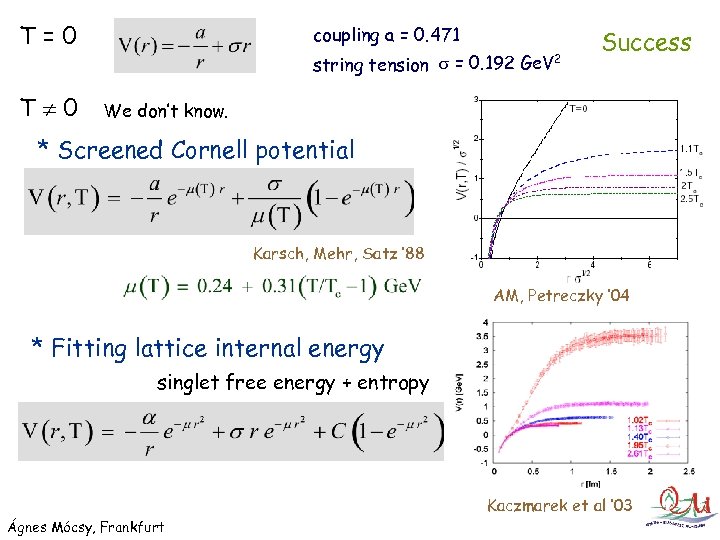
T=0 T 0 coupling a = 0. 471 string tension s = 0. 192 Ge. V 2 Success We don’t know. * Screened Cornell potential Karsch, Mehr, Satz ‘ 88 AM, Petreczky ‘ 04 * Fitting lattice internal energy singlet free energy + entropy Kaczmarek et al ‘ 03 Ágnes Mócsy, Frankfurt

resonances continuum threshold in vector channel static susceptibility diffusion/charge fluctuations Talk by P. Petreczky, Teaney 05 AM, Petreczky, in prep. T=0: energy above which no clear resonance observed experimentally T 0: above which q travel freely with mass mq(T) s 0 (T) = 2 mq(T) asymptotic value V 1(T) thermal energy for the qq pair Ágnes Mócsy, Frankfurt
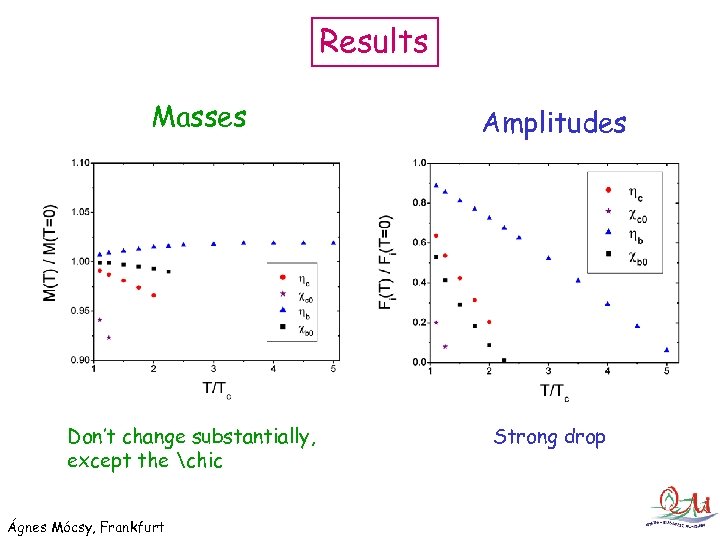
Results Masses Don’t change substantially, except the chic Ágnes Mócsy, Frankfurt Amplitudes Strong drop
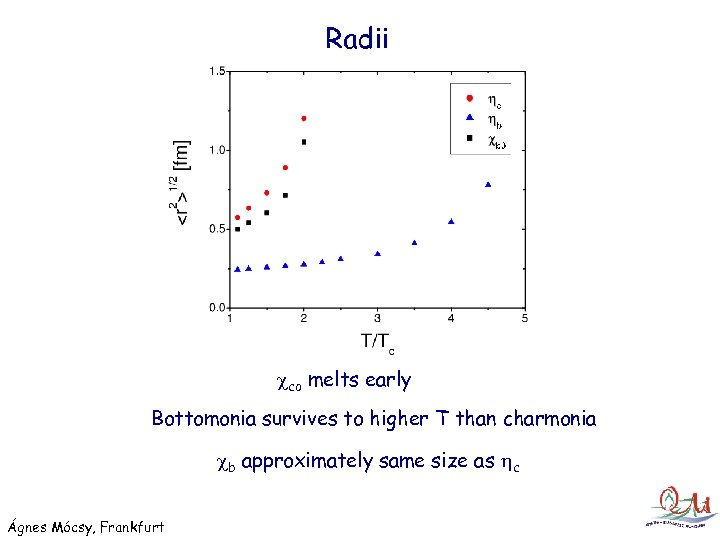
Radii co melts early Bottomonia survives to higher T than charmonia b approximately same size as c Ágnes Mócsy, Frankfurt
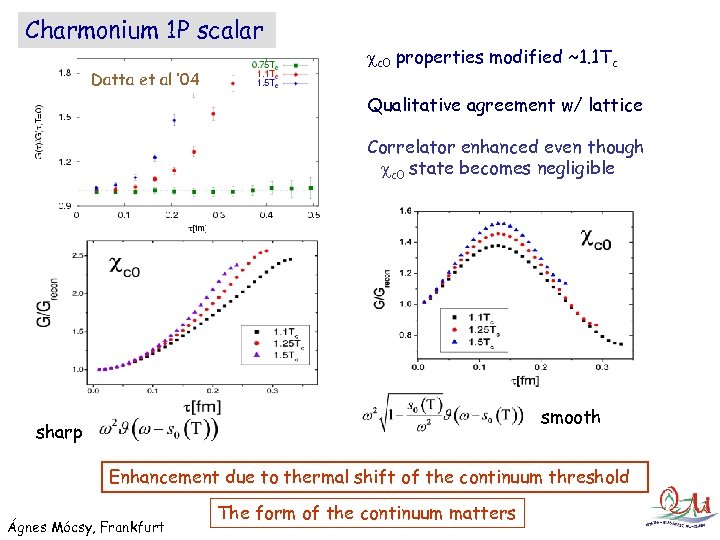
Charmonium 1 P scalar Datta et al ‘ 04 c 0 properties modified ~1. 1 Tc Qualitative agreement w/ lattice Correlator enhanced even though c 0 state becomes negligible smooth sharp Enhancement due to thermal shift of the continuum threshold Ágnes Mócsy, Frankfurt The form of the continuum matters
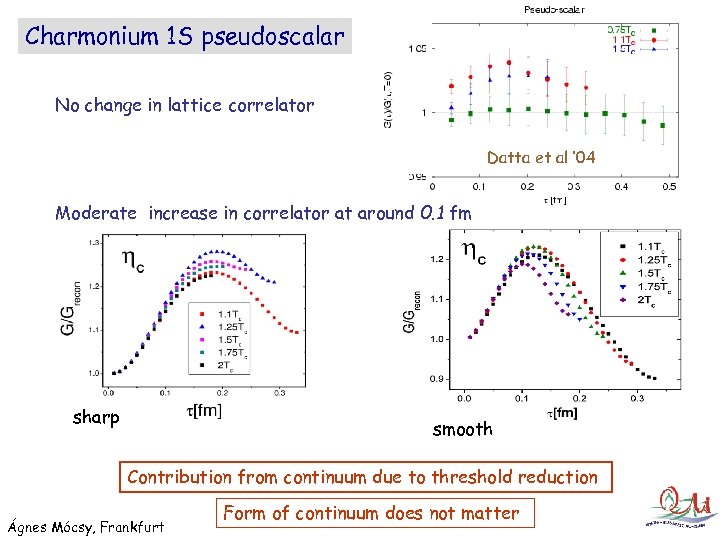
Charmonium 1 S pseudoscalar No change in lattice correlator Datta et al ‘ 04 Moderate increase in correlator at around 0. 1 fm sharp smooth Contribution from continuum due to threshold reduction Ágnes Mócsy, Frankfurt Form of continuum does not matter
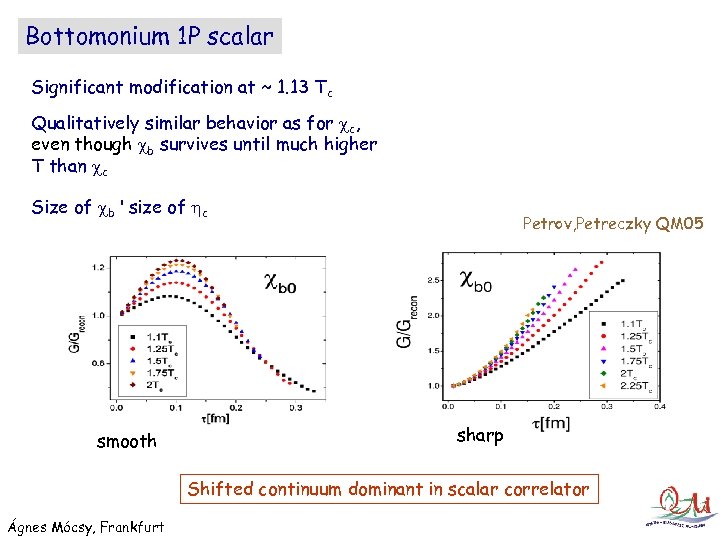
Bottomonium 1 P scalar Significant modification at ~ 1. 13 Tc Qualitatively similar behavior as for c, even though b survives until much higher T than c Size of b ' size of c smooth Petrov, Petreczky QM 05 sharp Shifted continuum dominant in scalar correlator Ágnes Mócsy, Frankfurt
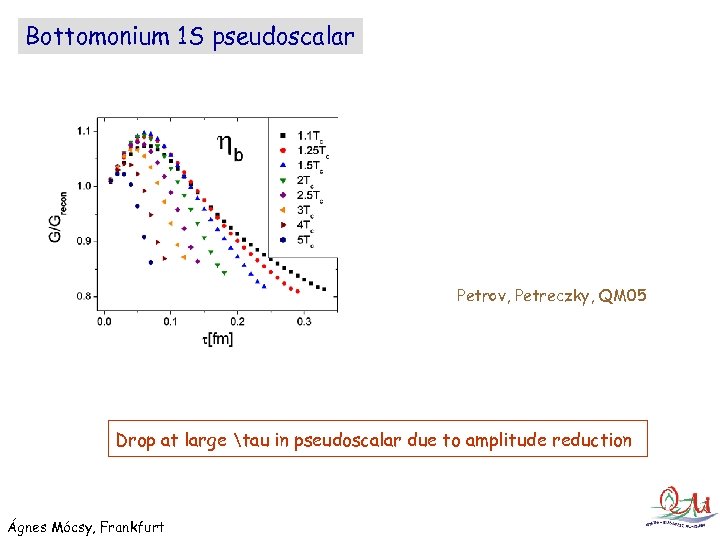
Bottomonium 1 S pseudoscalar Petrov, Petreczky, QM 05 Drop at large tau in pseudoscalar due to amplitude reduction Ágnes Mócsy, Frankfurt
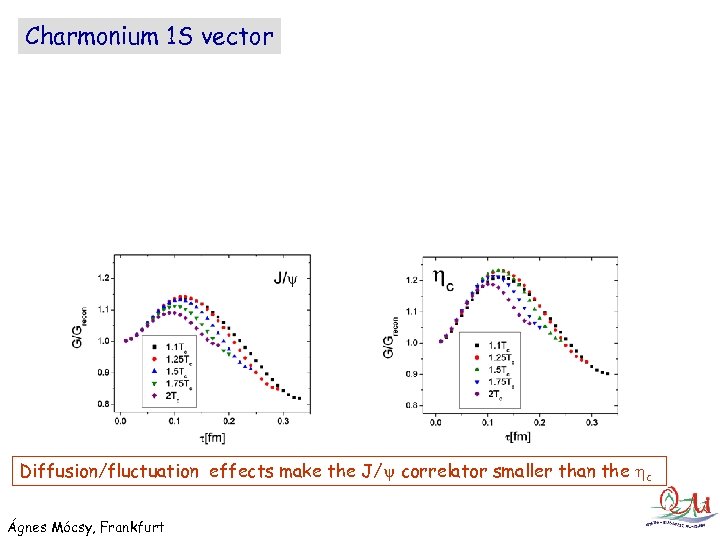
Charmonium 1 S vector Diffusion/fluctuation effects make the J/ correlator smaller than the c Ágnes Mócsy, Frankfurt
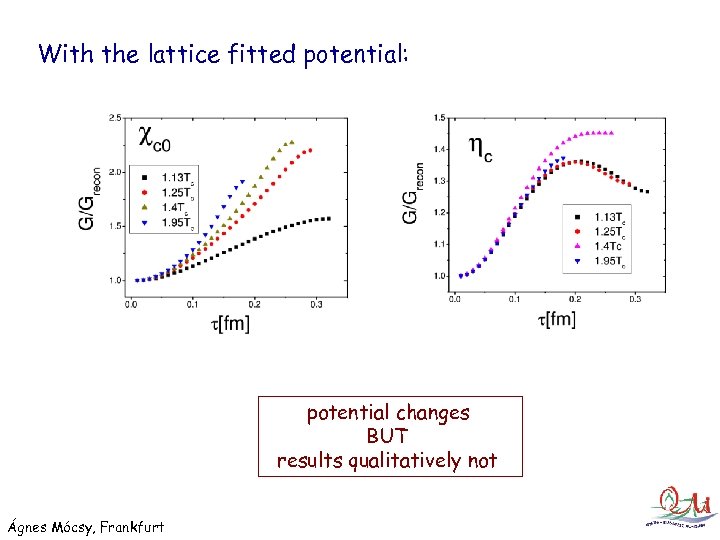
With the lattice fitted potential: potential changes BUT results qualitatively not Ágnes Mócsy, Frankfurt
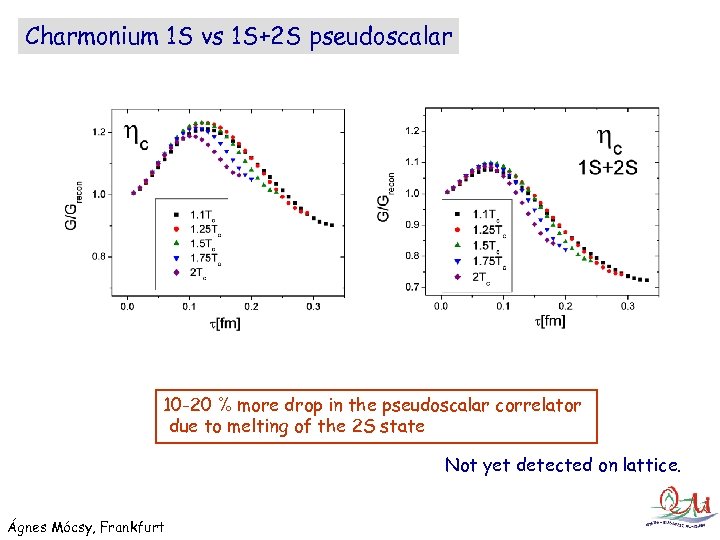
Charmonium 1 S vs 1 S+2 S pseudoscalar 10 -20 % more drop in the pseudoscalar correlator due to melting of the 2 S state Not yet detected on lattice. Ágnes Mócsy, Frankfurt
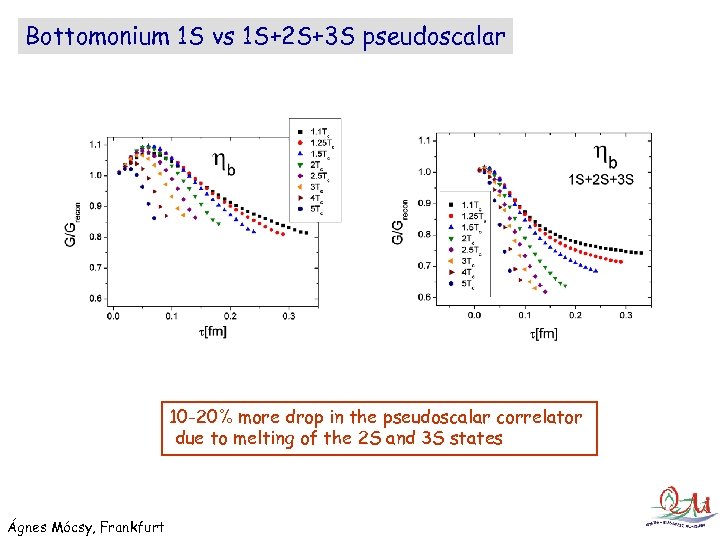
Bottomonium 1 S vs 1 S+2 S+3 S pseudoscalar 10 -20% more drop in the pseudoscalar correlator due to melting of the 2 S and 3 S states Ágnes Mócsy, Frankfurt

Summary Quarkonia melting at Tc - proposed sign for deconfinement challenged by lattice data – some quarkonia survives well above Tc First analysis of quarkonia correlators in potential model Tested w/ different potentials – no qualitative changes in the T-dependence of the correlators not in agreement with the lattice Increase in correlators – due to threshold decrease lattice doesn’t see Can medium effects on heavy quark boundstates be described by potential models? Do we miss some physics on the lattice? Ágnes Mócsy, Frankfurt
45558537ad125e8a01f09c138d2d7093.ppt