Quantum Theory Part 2 The Atom Is it

Quantum Theory, Part 2 The Atom Is it a particle or a wave? Day 1

Is it a particle or a wave? n Particle – Defined location at a particular time – Can be at rest, moving, or accelerating Falling Ball Ground level

Is it a particle or a wave? n Wave – Need to see crests and troughs to define them. – Waves are oscillations in space and time. Direction of travel, velocity Up-down oscillations Wavelength, frequency, velocity and oscillation size defines waves 3

Basic difference in behaviour? When particles collide, they cannot pass through each other. They can bounce or they can shatter! Before collision After collision Before collision Another after collision state shatter 4

Watch the collision between a truck with ladder on top and a car at rest ! Note the ladder continue its motion forward …. . 5

Head on collision of a car and truck Collision is inelastic – the small car is pushed along by the truck…… 6

The basic difference between Waves and Particles: - Waves can pass through each other! - As they pass through, they can enhance or cancel each other. -Afterwards, they regain their original form 7

Waves and Particles: Spread in space and time Waves Can be superposed – show interference effects Pass through each other Localized in space and time Particles Cannot pass through each other they bounce or shatter. 8

What is Light? !? !? n Planck’s Experiment PARTICLE! Blackbody Radiation – energy is quantized n Einstein’s Experiment PARTICLE! Photoelectric Effect – light is made up of photons.

Laser

If light is a particle then….

Thomas Young n Performed the Double Slit Experiment to test the wave nature of light.

INTERFERENCE (2 D) + = Constructive Interference = more intense (brighter) wave + (AMPLIFIED) = Destructive Interference = no amplitude (Node) meaning no wave (CANCELED)

A prism bends light. Different Colors are bent by different amounts. White Light

Two source interference constructive interference ------destructive interference -------

Two source interference Path difference = S 2 P – S 1 P = 1 wavelength = constructive interference ------destructive interference ------- P S 1 S 2

Two source interference Path difference for constructive interference = n (where n is an integer) 0 2 3 constructive interference ------destructive interference -------

Two source interference Path difference for destructive interference = (n + ½) (where n is an integer) ½ 1½ 2½ constructive interference ------destructive interference -------

Interference in the Experiment

Young’s Double Slit Experiment

CONCLUSION: Light is a wave!

Well along came Louis de Broglie and he said if light can travel in waves and act like particles (energy is given off in packets, called photons) perhaps matter, which is composed of particles can act like waves. This became known as the Wave-Particle Duality, which led to Quantum mechanics and the discussion that the electron, which is a particle, can move like a wave. mparticle = h / v (v is velocity) particle = h / m v h = 6. 626 x 10 -34 Js = wavelength in m m = mass in kg v = velocity in m/s

An electron has mass, so it is matter. A particle can only go through one hole, a wave through both holes. An electron does go through both, and makes an interference pattern. Thus, it behaves like a wave. Electrons exhibit wave like properties – they can pass through each other! Phenomenon of electron interference In fact in 1927, a beam of electrons was able to be diffracted thus suggesting that like light, electrons travel in waves. ONLY waves CAN BE DIFFRACTED. (This experimental evidence helped prove de Broglie’s ideas. ) NOTE: Because de Broglie’s hypothesis is applicable to all matter, any object has the characteristics of waves, however the wavelength of an ordinary sized object, such as a golf ball, is so tiny, that it cannot be observed by the human eye.

Dual Nature of Light Waves can bend around small obstacles… …and fan out from pinholes. Particles effuse from pinholes Three ways to tell a wave from a particle… wave behavior particle behavior waves interfere particle collide waves diffract particles effuse waves are delocalized particles are localized

This quantum picture of the world is at odds with our common sense view of physical objects. We cannot uniquely define what is a particle and what is a wave !!

TRUE UNDERSTANDING OF NATURE REQUIRED THAT PHYSICAL OBJECTS, WHATEVER THEY ARE, ARE NEITHER EXCLUSIVELY PARTICLES OR WAVES No experiment can ever measure both aspects at the same time, so we never see a mixture of particle and wave. WHEN ONE OBSERVES A PHYSICAL PHENOMENON INVOLVING A PHYSICAL OBJECT, THE BEHAVIOUR YOU WILL OBSERVE – WHETHER PARTICLE LIKE OR WAVE LIKE – DEPENDS ON YOUR METHOD OF OBSERVATION. THE OBJECT IS DESCRIBED BY MATHEMATICAL FUNCT IONS WHICH ARE MEASURES OF PROBABILITY. 34

ALL PHYSICAL OBJECTS exhibit both PARTICLE AND WAVE LIKE PROPERTIES. THIS WAS THE STARTING POINT OF QUANTUM MECHANICS DEVELOPED INDEPENDENTLY BY ERWIN SCHRODINGER AND WERNER HEISENBERG.

Classical world is Deterministic: • Knowing the position and velocity of all objects at a particular time • Future can be predicted using known laws of force • and Newton's laws of motion. Quantum World is Probabilistic: • Impossible to know position and velocity with certainty at a given time. • • Only probability of future state can be predicted using known laws of force and equations of quantum mechanics. Tied together Observed 36

BEFORE OBSERVATION IT IS IMPOSSIBLE TO SAY WHETHER AN OBJECT IS A WAVE OR A PARTICLE OR WHETHER IT EXISTS AT ALL !! QUANTUM MECHANICS IS A PROBABILISTIC THEORY OF NATURE

Heisenburg’s Uncertainty Principle In order to find the location or momentum (velocity) of the electron, the investigator must interact with the electron. Heisenberg’s uncertainty principle states you can never know both the location of an electron and its momentum (velocity). If you know the velocity, then you will not know the location; likewise, if you know the location, you cannot know the velocity. Scientists do not know the exact path that an electron will follow.

Heisenberg Uncertainty Principle n n In order to observe an electron, one would need to hit it with photons having a very short wavelength. Short wavelength photons would have a high frequency and a great deal of energy. If one were to hit an electron, it would cause the motion and the speed of the electron to change. Lower energy photons would have a smaller effect but would not give precise information.

The Quantum Mechanical Model n Charge Cloud Model – Erwin “Werner” Schrödinger » Austrian n n Energy is quantized. It comes in chunks. Schrödinger derived an equation that described the energy and position of the electrons in an atom.

Modern View n n n The atom is mostly empty space. Electrons do not follow circular paths. Energy levels are 3 -dimensional. Model is based on the probability of finding an electron a certain distance from the nucleus Two regions – Nucleus- protons and neutrons. – Electron cloud- region where you might find an electron.

So, unlike the Bohr theory of the atom, the modern quantum theory of the atom does not show the electrons following circular orbits, but shows the regions in which there is a high probability of finding an electron. These regions are called orbitals (90% probability). This new theory of wave mechanics, or quantum mechanics, was credited to Erwin (Werner) Schrödinger. In your junior year in college, in physical chemistry you will spend 15 weeks studying the mathematics behind Schrödinger’s equation. (In fact, he was given the 1932 Nobel Prize in Physics for it. ) Electron cannot destructively interfere with itself These equations are used to determine the probability of finding a particle at a particular time and a particular place; hence, the location of the electron. Schrödinger’s work shows how the probability of finding the electron varies within the atom.

QUANTIZED WAVELENGTHS Fundamental mode 200 Second Harmonic or First Overtone 200 Standing Wave 200 150 150 100 100 50 50 50 0 - 50 -100 -150 -200 0 50 100 150 200

Electrons as Waves QUANTIZED WAVELENGTHS n=5 n=4 n=6 Forbidden n = 3. 3

Schrodinger’s Cat

A compilation of individual electrons • The visual concept of the atom now appeared as an electron "cloud" which surrounds a nucleus. • The cloud consists of a probability distribution map • Determines the most probable location of an electron. • For example, if one could take a snap-shot of the location of the electron at different times and then superimpose all of the shots into one photo, then it might look something like the view at the top.

Scientists are able to plot the changing probability as points as a threedimensional representation. You will find that regions with high probability have a dense set of points, while areas of low probability have points that are more spread out. These plots look like diffuse clouds. Thus leading to the present day name of the model of the atom, Charge-cloud. Solving various wave equations led us to the location and motion of the electron inside the atom. A set of four(4) quantum numbers describe the probability (orbitals) of finding the electron at a certain spot in the atom. Using these four quantum numbers, we are able to describe the energy level, sublevel, orbital, etc. of each electron.

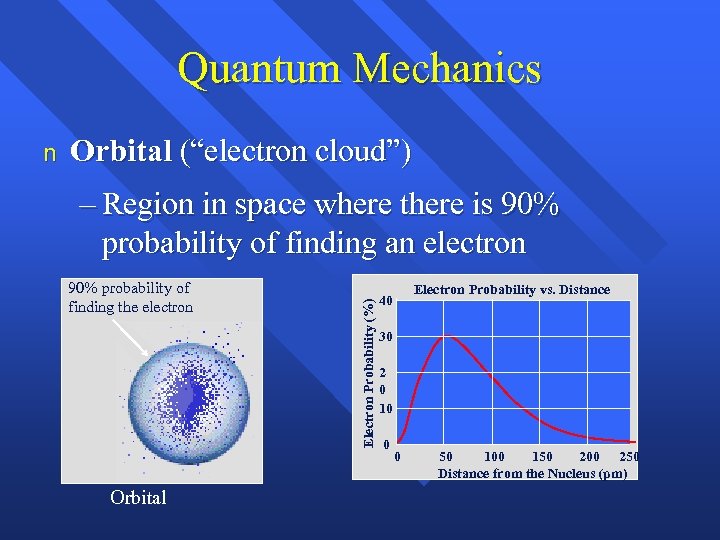Quantum Mechanics Orbital (“electron cloud”) – Region in space where there is 90% probability of finding an electron 90% probability of finding the electron Orbital Electron Probability (%) n Electron Probability vs. Distance 40 30 2 0 10 0 0 50 100 150 200 250 Distance from the Nucleus (pm)

Shapes of s, p, and d-Orbitals s orbital p orbitals d orbitals

Atomic Orbitals

s, p, and d-orbitals A s orbitals: Hold 2 electrons (outer orbitals of Groups 1 and 2) B p orbitals: Each of 3 pairs of lobes holds 2 electrons = 6 electrons (outer orbitals of Groups 13 to 18) C d orbitals: Each of 5 sets of lobes holds 2 electrons = 10 electrons (found in elements with atomic no. of 21 and higher)

(a) Electron probability (b) Contour probability (c) Radial probability

r r r Distance from nucleus (a) 1 s (b) 2 s (c) 3 s

Quantum Numbers y y z x px y z x pz py

p-Orbitals px pz py

y z x s 2 s y y z x px y z x pz 2 p (x, y, z) py carbon

Electron configurations: Labeling electrons in atoms Quantum numbers are directions (like an address) to find the location of an electron. State: City: Street: House: Energy Level (n = 1, 2, 3, …, 7) Sublevel (s, p, d, f) Orientation of orbital (axis) Spin (+1/2 or – 1/2)

The First Quantum Number The first quantum number is called the primary or principal quantum number, represented by the letter n. This number describes which energy level the electron occupies. n = 1, 2, 3, 4, 5, 6, or 7. A large number indicates more energy and a greater distance from the nucleus. n 2 = # of orbitals in the energy level

Relative Sizes 1 s and 2 s 1 s 2 s

The Second Quantum Number The second quantum number (azimuthal or angular momentum quantum number) describes the shape of the orbital. s, p, d, f. These letters just represent the shape of the orbitals. s (sharp) is a sphere; p (principal) is shaped like a dumbbell; d (diffuse) and f (fundamental) have complex shapes and higher energy. The number of possible orbital shapes in an energy level = the value of n n 1 2 3 4 : n orbital shapes s s, p, d, f n shapes possible

The Second Quantum Number The azimuthal quantum number is represented by the letter l l describes the shape of the region of space occupied by the Value of electron Allowed values of from 0 l depend on the value of n and can range to n– 1 All wave functions that have the same value of both n and subshell l form a Regions of space occupied by electrons in the same subshell have the same shape but are oriented differently in space

l=0 p s l=2 d l=3 f l=1

Quantum Numbers Principal level n=1 Sublevel s Orbital n=2 s p px py pz n=3 s p px py pz • n = # of sublevels per level • n 2 = # of orbitals per level • Sublevel sets: 1 s, 3 p, 5 d, 7 f d dxy dxz dyz dz 2 dx 2 - y 2

Maximum Capacities of Subshells and Principal Shells n 1 2 l 0 0 1 2 3 Subshell designation s s p d f Orbitals in subshell 1 1 3 5 7 Subshell capacity 2 2 6 10 14 Principal shell capacity 2 8 3 18 4 32 . . . n . . . 2 n 2

The Third Quantum Number The third quantum number, magnetic quantum number is represented by ml. This number tells you the spatial orientation (position) of the orbital that the electron occupies along the x, y, or z plane. Allowed values of ml depend on the value of ml can range from –l l to l in integral steps ml = l, - l + l, . . . 0. . . , l – 1, l Each wave function with an allowed combination of n, l, and ml values describes an atomic orbital, a particular spatial distribution for an electron

The Third Quantum Number For a given set of quantum numbers, each principal shell contains a fixed number of subshells, and each subshell contains a fixed number of orbitals. The s sublevel contains one (1) s orbitals. The s sublevel may hold two (2) electrons. The p sublevel contains three (3) p orbitals. The p sublevel may hold six (6) electrons. The d sublevel contains five (5) d orbitals. The d sublevel may hold ten (10) electrons. The f sublevel contains seven (7) f orbitals. The f sublevel may hold fourteen (14) electrons.

If l = 2 (d orbital) Then ml = -2, l, -1, - l + l, . . . 0, 0. . . , 1, l – 1, 2 l

The Fourth Quantum Number The fourth quantum number, spin quantum number, tells you the direction of the electron’s spin (+1/2 or – 1/2) clockwise or counter-clockwise So, the 4 quantum numbers tell you: 1. 2. 3. 4. The principal energy level The shape of the orbitals The orientation of the orbital The spin of the electron

Allowed Sets of Quantum Numbers for Electrons in Atoms Level n 1 l 0 0 Sublevel Orbital ml Spin ms = +1/2 = -1/2 2 0 0 1 3 1 0 -1 0 0 1 1 0 -1 2 0 -1 -2

Electron Orbitals: Electron orbitals Equivalent Electron shells (a) 1 s orbital (b) 2 s and 2 p orbitals c) Neon Ne-10: 1 s, 2 s and 2 p

Quantum Numbers n shell 1, 2, 3, 4, . . . l subshell 0, 1, 2, . . . n - 1 ml orbital - l. . . 0. . . +l ms electron spin +1/2 and - 1/2

Electron Configurations

Aufbau Principle states that when filling an atom with electrons, the lowest energy levels, sublevels, and orbitals must be filled before proceeding to the next level. In atoms of different elements, the arrangement of electrons in orbitals follows a precise pattern. The electrons enter orbitals in order of increasing energy of the orbitals, beginning with the 1 s orbital. At higher energy levels, some orbitals overlap. 1 s 2 s 2 p 3 s 3 p 4 s 3 d 4 p 5 s 4 d 5 p 6 s Pauli Exclusion Principle states that no two electrons can have the same 4 quantum numbers. Hund’s Rule states that the most stable arrangement of the electrons is that with the maximum number of unpaired electrons, all with the same spin directions. Degenerate orbitals: same amount of energy, the 3 p orbitals, the 5 d orbitals, the 7 f orbitals, etc.

How to write an electron configuration: Electron Configuration: description of the arrangement of electrons in an atom • Locate the element whose electron configuration you wish to write in the periodic table. • Fill orbitals in the proper order with electrons. • Check that the total number of electrons in the electron configuration equals the atomic number.

s sublevel contains 1 s orbital. p sublevel contains 3 p orbitals d sublevel contains 5 d orbitals f sublevel contains 7 f orbitals A circle stands for an orbital. This is an empty orbital. This is an orbital with 1 electron in it. This is an orbital with 2 electrons in it. (Notice the opposite spins)

Each orbital can hold a maximum of 2 electrons!!!! This is an orbital with 2 electrons in it. (Notice the opposite spins) Hence, s sublevel has 1 orbital therefore it can hold 2 electrons (s 1 and s 2) p sublevel has 3 orbitals therefore it can hold 6 electrons (p 1 to p 6) d sublevel has 5 orbitals therefore it can hold 10 electrons (d 1 to d 10) f sublevel has 7 orbitals therefore it can hold 14 electrons (f 1 to f 14)

To write an electron configuration, you must know the number of electrons in an atom. This is the same number as Z, the atomic number of the element. SPECTROSCOPIC Hydrogen (Z=1) 1 s 2 s 2 p 3 s 3 p 1 s 1 Helium (Z=2) 1 s 2 s 2 p 3 s 3 p Lithium (Z=3) 1 s 2 s 2 p 3 s 3 p Beryllium (Z=4) 1 s 2 s 2 p 3 s 3 p Boron (Z=5) 1 s 2 s 2 p 3 s 3 p NOTATION 1 s 22 s 1 1 s 22 s 22 p 1 ORBITAL DIAGRAMS

Carbon (Z=6) 1 s 2 s *Hund’s Rule Nitrogen (Z=7) 2 p* 3 s 3 p xyz 1 s 2 s 2 p* 1 s 22 p 3 *Hund’s Rule Oxygen (Z=8) *Hund’s Rule 1 s 22 p 2 1 s 2 s 2 p* 3 s 3 p 1 s 22 p 4

Skipping around the table…………… Potassium (Z=19) 1 s 2 s 3 s 3 p 4 s 3 d 1 s 22 p 63 s 23 p 64 s 1 Calcium (Z=20) 1 s 2 p 2 s 2 p 3 s 3 p 4 s 3 d 1 s 22 p 63 s 23 p 64 s 2 Scandium (Z=21) 1 s 2 s 2 p 3 s 3 p 4 s 1 s 22 p 63 s 23 p 64 s 23 d 1 3 d

Shorthand Configuration NOBLE GAS METHOD A neon's electron configuration (1 s 22 p 6) B third energy level [Ne] 3 s 1 C one electron in the s orbital D Na = [1 s 22 p 6] 3 s 1 orbital shape electron configuration

32 Ge Periodic Patterns n 72. 61 Example - Germanium 2 [Ar]4 s 10 3 d 2 4 p

Shorthand Configuration Element symbol Electron configuration Ca [Ar] 4 s 2 V [Ar] 4 s 2 3 d 3 F [He] 2 s 2 2 p 5 Ag [Kr] 5 s 2 4 d 9 I [Kr] 5 s 2 4 d 10 5 p 5 Xe [Kr] 5 s 2 4 d 10 5 p 6 Fe Sg 22 p 6 4 s 3 p 64 s [He] 2 s[Ar]3 s 223 d 6 [Rn] 7 s 2 5 f 14 6 d 4

KERNAL (Core of atom) includes the nucleus and the energy levels, EXCEPT the outermost (valence level). VALENCE is the outermost energy level. LEWIS DOT STRUCTURES: • Write the chemical symbol. • Indicate the number of electrons in the valence shell using dots around the symbol. 4 7 63 X 58 1 2

Notation n Longhand Configuration S 16 e- 1 s 2 2 p 6 3 s 2 3 p 4 Core Electrons Valence Electrons • Shorthand Configuration S 16 e 2 3 p 4 [Ne] 3 s S 16 32. 066

Electron Dot Diagrams Group 1 1 A 2 2 A 13 3 A 14 4 A 15 5 A 16 6 A 17 7 A H 18 8 A He Li Be B C N O F Ne Na Mg Al Si P S Cl Ar K Ca Ga Ge As Se Br Kr s 1 s 2 p 2 s 2 p 3 s 2 p 4 s 2 p 5 s 2 p 6 = valence electron

Recall the electron configuration for Oxygen (in its ground state): 1 s 2 s 2 p 3 s 3 p When we add heat to oxygen, an electron absorbs the energy and jumps to a higher energy state which is shown below: 1 s 2 s or, it can be shown as: 1 s 2 s 2 p 3 s 3 p There are certain rules of stability that affect the electron configurations of all of the elements; thus, certain arrangements of electrons are more stable than others. However, these last two arrangements are unstable. Therefore the electron must return to its ground state. It accomplishes this by emitting the absorbed energy as visible light (color) within the EM spectrum.

The most stable arrangement is that of a full energy level. *** He Ne Ar Kr 1 s 2 *** 2 s 22 p 6 3 s 23 p 6 4 s 23 d 104 p 6 (etc, etc. ) Elements that have this arrangement belong to the Noble gas ____________ family.

Second most stable arrangement is that of a full sublevel. Mg Ca Sr Ba 2 s 2 3 s 2 4 s 2 5 s 2 (etc, etc. ) Elements that have this arrangement belong to the ____________ Alkaline Earth Metal family.

Third most stable arrangement is that of a half-full sublevel. H Li Na K 1 s 1 2 s 1 3 s 1 4 s 1 (etc, etc. ) Elements that have this arrangement belong to the _____________ family. Alkali Metal N P As Sb 2 s 22 p 3 3 s 23 p 3 4 s 24 p 3 5 s 25 p 3 (etc, etc. ) Elements that have this arrangement belong to the _____________ family. Pictinogen Finally, the least stable arrangement is that of no particular order.

Here a few special cases: What would you predict to be the electron configuration for Chromium (Cr)? 1 s 2 s 2 p 3 s 3 p 4 s 3 d Is that a particularly stable arrangement? ____ In fact, we can rearrange the electrons to make a more stable configuration !!!!!!! 1 s 2 s 2 p 3 s 3 p 4 s 3 d Why would this be a particularly stable arrangement? In fact, every element in Group 6 (VIB) will arrange its electrons so that it has this type of configuration. (s 1 d 5)

What would you predict to be the electron configuration for copper (Cu)? 1 s 2 s 2 p 3 s 3 p 4 s 3 d Like Cr, Cu will rearrange its configuration to become more stable. Why is this configuration very stable? In fact, every element in Group 11 (IB) will arrange its electrons so that it has this type of configuration. (s 1 d 10)

The Octet Rule Atoms tend to gain, lose, or share electrons until they have eight valence electrons. This fills the valence shell and tends to give the atom the stability of the inert gasses. ONLY s- and p-orbitals are valence electrons.

Stability n Ion Electron Configuration – Write the e- configuration for the closest Noble Gas » EX: Oxygen ion O 2 - Ne O 2 - 10 e- [He] 2 s 2 2 p 6

Magnetism Diamagnetic • No unpaired electrons in the orbital diagram • Diamagnetic materials are not magnetic Paramagnetic • The atom has unpaired electrons in its orbital diagram • Electron spins will align in an external magnetic field • Magnetism • Al. Ni. Co Magnets • Increasing the # of unpaired electrons = increase in magnetism Ferromagnetic • Many unpaired electrons in the orbital diagram • These materials can remain magnetic after the external magnetic field is removed • Electron spins trend to align spontaneously without any applied field • Fe, Co, Ni • Rare-earth magnets – lanthanide series of f orbitals

Can a Tattoo React with Magnetic Resonance Imaging (MRI)? • The magnetic force of an MRI machine is so strong, even the “weakest” machine is 10, 000 times the strength of the Earth’s magnetic field. • Yes, there is medical evidence that a tattoo can cause a reaction during an MRI. • The tattoo inks expected to cause a reaction are those containing iron oxide (some black, brown, red, flesh, yellow, orange). • Magnetic metals can convert the radio-frequency pulses of an MRI machine into electricity. • The burning sensation felt at the site of the tattoo may be a result of electricity running through the tattoo or from the ‘pull' exerted on the magnetic material in the tattoo. • To reduce the possibility of burning, your doctor may recommend placing ice packs or cool compresses over your tattoos during the MRI. • MRI’ s affect any magnetic material on or in your body • Jewelry, Implants (dental or otherwise), Pacemakers or even metal fragments. • Even small metal objects such as paperclips or keys can become projectile weapons if left in an MRI room during a scan.