Quantum Public Key Cryptography with Information Theoretic Security

Quantum Public Key Cryptography with Information. Theoretic Security Daniel Gottesman Perimeter Institute

Advantages of Public Key Crypto • High efficiency • New protocols o Public key encryption o Digital signatures • Better key distribution and management o No danger that public key compromised o Convert authenticated channel to secure channel in interactive setting (QKD can do this too) o Certificate authorities o PGP (many redistribution sites)

Quantum Public Keys Consider a map f: k fk. • k is the private key • fk is the public key For some maps f, it can be impossible (information-theoretically) to determine k, even given many copies of fk. However, there is a limit. More copies of fk means more information about k, and even one copy generally leaks some information about k.

Quantum Fingerprinting For example, we can let k be an O(2 n)-bit string and fk be n qubits long using quantum fingerprints (Buhrman, Cleve, Watrous, de Wolf 2001). One construction: Let C be a [2 n, r 2 n, p 2 n] code, with max dist. (1 -p)2 n, and let x (k, i) be the ith bit of the codeword encoding k. Then fk = 2 -n/2 i (-1)x(k, i) i , which implies that fj fk 1 -2 p (when i j).

Quantum One-Way Function From n qubits, we can extract at most n classical bits of information, so T copies of fk can only give at most Tn bits of information about k, which is r 2 n bits long. Thus, the function f: k fk is hard (impossible, actually) to invert, even given many copies of the output. It is a one-way function. This is why it is safe to use fk as a public key: we can give it to many people without revealing the private key k.

One-Time Digital Signature Classical scheme (Lamport 1979): One-way function f(x), private key (k 0, k 1), public key (f(k 0), f(k 1)). To sign a bit b, send (b, kb). Quantum scheme (Gottesman, Chuang 2001): • Private key (k 0(i), k 1(i)) (i=1, . . . , M) • Public key ( fk ) (for k=kb(i)) • To sign b, send (b, kb(1), kb(2), . . . , kb(M)). • To verify, measure fk to check k = kb(i).

Different Levels of Acceptance Suppose s keys fail the measurement test: s c 1 M 1 -ACC: Message comes from Alice, other recipients will agree. c 1 M < s c 2 M 0 -ACC: Message comes from Alice, another recipient might disagree. s > c 2 M REJ: Message might not come from Alice. Similar to classical pseudo-signatures (Chaum and Roijakkers 1991), which are information-theoretically secure, but with complex set-up procedure.

Quantum Public Key Encryption • Protocol defines map k Uk (unitary) • Alice’s private key k • Public key (I Uk) ( 0 0 + 1 1 ) • To encrypt a quantum state , teleport state through the public key, getting Pauli matrix P. Transmit P and 2 nd register of public key. • Alice receives (P, Uk P ). Decrypts by performing Uk-1 then P-1.

Notes on Quantum Public Key Encryption • Expends one copy of the public key per encrypted message. • When Uk runs over Pauli matrices, this is the one-time pad, but only one copy of public key is allowed. • For larger sets of Uk, it is impossible to learn k completely. However, I have no security proof.

SWAP test BCWW also introduced a test to check if two fingerprints are the same without knowing their exact state: 0 + 1 fj fk Controlled-SWAP Measure 0 + 1 vs. 0 - 1 fj fk • If they are the same, + result (fingerprints are unchanged) • If they are different, often - result

Distributed SWAP Test Two problems with the straight SWAP test: • How can we do a SWAP test at a distance? • A SWAP test against a bad key corrupts your copy. Distributed SWAP test: keep key 1 SWAP key Bob 2 SWAP discard key 1 SWAP key Charlie

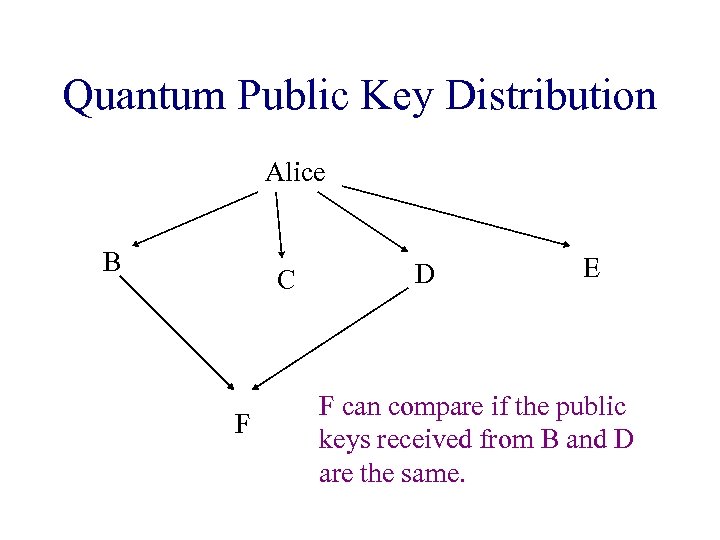
Quantum Public Key Distribution Alice B C F D E F can compare if the public keys received from B and D are the same.

Certificate Authorities A certificate authority signs other people’s public keys. Everyone has the CA’s public key already, and they trust the CA to verify the public key’s source. Main advantage: the CA only needs to be involved in the distant past. Can we make a certificate authority for quantum public keys?

No Signatures of Quantum States There is no signature scheme for unknown quantum states, even with computational security. Anyone who can read the signed state can change it. (BCGST 2002) Let Sk( ) be the signed state for (purified). To read the state, use U: Sk( ) Rk( ). But No-Cloning implies Rk( ) = Rk does not depend on . U To cheat: Sk( ) Rk U-1 Rk Sk( )

Signing Known Quantum States However, this argument does not apply to a state which is known by the signer, or even if the signer has multiple copies of . Can we sign a known quantum state? Yes, sort of: we can sign the classical description of the state. What we really want is to sign the state efficiently in the number of qubits. Can we do this? Unknown.

Signing Known Quantum States Solutions to this problem could potentially allow: • More efficient quantum signatures: sign a fingerprint of the classical message. • Reusable quantum signatures: sign a message plus a new quantum public key. • Quantum certificate authority: Provide multiple copies of your public key to the CA, allowing him to sign them.

Quantum Signature Efficiency One-time quantum signatures are very inefficient, but if it is possible to sign known states as suggested on the previous slide, they could become very efficient. • Key length to sign n-bit message: O(log n)? • Number of messages from single key: exp. ? • However: length of private key is still proportional to # of copies of public key. None of this is proved.

Capabilities of Quantum Public Keys • High efficiency (No? ) • New protocols o Public key encryption (Yes? ) o Digital signatures (Yes) • Better key distribution and management o No danger that public key compromised (Yes) o Convert authenticated channel to secure channel (Yes, QKD) o Certificate authorities (Yes? ? ) o PGP (many redistribution sites) (Yes)