2686f5c632a5dcaae113b0969a625846.ppt
- Количество слайдов: 35

Quantum computing with Rydberg atoms Klaus Mølmer Coherence school Pisa, September 2012

Quantum computing with Rydberg atoms Klaus Mølmer Coherence school Pisa, September 2012

Quantum Computing with Rydberg atoms Contents: • Introduction to Quantum Computing • Physical implementations • Rydberg atom quantum computing

• Reality: • Dream: Intel® Pentium® Dual Core T 4200 -processor, 2, 0 GHz, 3072 MB SDRAM. (250 GB harddisk) 650 Euros. Quantum computer Processor unknown 1 k. Hz is fine, 100 Hz is OK 1 kbit RAM would be great ! Buy at 108 Euros
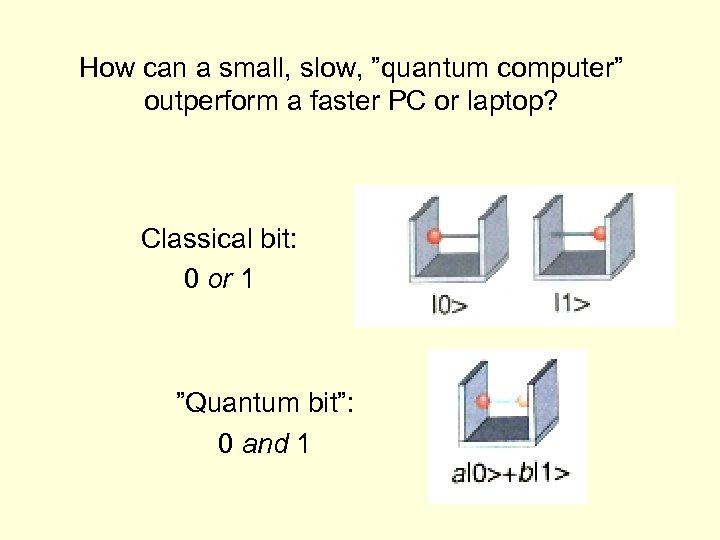
How can a small, slow, ”quantum computer” outperform a faster PC or laptop? Classical bit: 0 or 1 ”Quantum bit”: 0 and 1
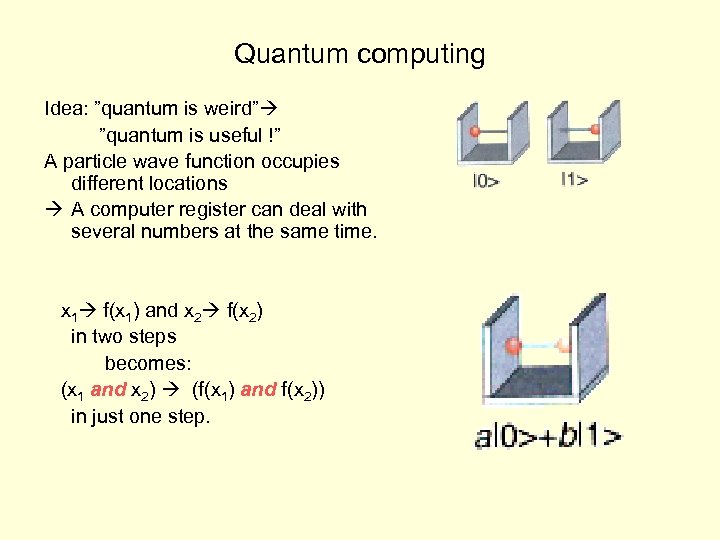
Quantum computing Idea: ”quantum is weird” ”quantum is useful !” A particle wave function occupies different locations A computer register can deal with several numbers at the same time. x 1 f(x 1) and x 2 f(x 2) in two steps becomes: (x 1 and x 2) (f(x 1) and f(x 2)) in just one step.

Measurements constitute a fundamental limitation. We cannot measure state, a|0>+b|1>. We can ask: ”Is the system in state |0> ? ” and the answer is Yes with probability |a|2 , and the state becomes |0> No with probability |b|2 , and the state becomes |1> |a|2+|b|2=1 You get random answers, and you do not learn more by asking twice !

Parallel processing on a single quantum computer • a|x 1> +b|x 2> a|f(x 1)> + b|f(x 2)> • All x, Σx cx |x> Σx cx |f(x)>, all f(x) by a single iteration of a single quantum register. We only need to solve two problems: • readout: how to get all f(x) and not just a random f(x) ? (algorithms) Shor and Grover ! • construction: how to build and control a mikroscopic quantum system ? (physics)

Is a computational problem easy or hard? How do the ressources needed scale with the problem size? • Addition: 1 1 1 246389135 +358901246 =605290381 needs L operations for L-digit numbers • Multiplication: 246389135 x 358901246= needs L 2 operations for L-digit numbers

Harder problems: • Find an element out of N, who fulfils a certain condition: max: N trials, average: N/2 attempts √N • Find factors of an integer N trial and error: does 2 factor M ? does 3 ? , … until √M (max): ~ √M attempts Let M ~ 10 L (L digit number), then √M ~ (√ 10)L ~ exp(L) (exponentially hard) L 3 Quantum computer new scaling !!! Shor 1994, Grover 1997, other ”single-output” problems

Shor’s algorithm Find factor of stort large N N=15 • Pick random a • a=2 20 • 1, 2, 4, 22=4, 2 3=8, =1, 21=2, 8, 1, 2. . • Let f(x) = ax mod N =16 • f(x) is periodic, f(x+p)=f(x) 24 • p=41, 25=32 2, … • Determine numbers ap/2 ± 1 • 22 ± 1 = 3 or 5 • One of these numbers • 3 factors 15 factors N 5 factors 15 • Check ! (easy) • Yes ! If you fail, try another a

Arizon 005 ebruary 2. F y Star, 20 a Dail

Rydberg blockade and quantum information Grover: 1) Σcx |x> Σ (-1) f(x) cx |x> (-1) if x matches the “marked“ x 0 2) Inversion of cx about their mean. x

Rydberg blockade and quantum information Grover: 1) Σcx |x> Σ (-1) f(x) cx |x> (-1) if x matches the “marked“ x 0 2) Inversion of cx about their mean. ~3/√N 1/√N x Repeat √N times Quantum systems can explore the Hilbert space of superposition states, and they can ”converge” on solutions to hard problems. Must implement the calculations on a physics quantum system !

Re-cycle classical computing paradigm • Computers represent information (data) in binary form (bits), • example. : 5 =1*22+0*21+1*20 =’ 101’ • All data manipulations are evaluations of functions based on operations that decompose as single-bit and bit-pair logical operations: NOT, AND, OR …. |0> |1> NOT |1> |0>
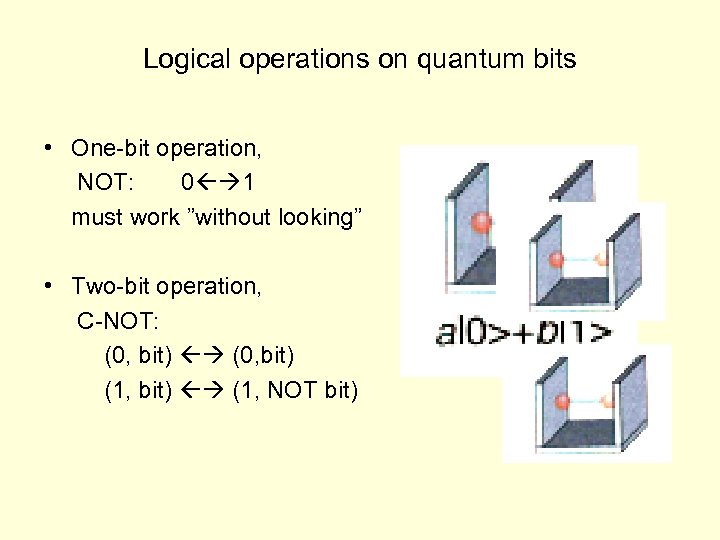
Logical operations on quantum bits • One-bit operation, NOT: 0 1 must work ”without looking” • Two-bit operation, C-NOT: (0, bit) (1, bit) (1, NOT bit)
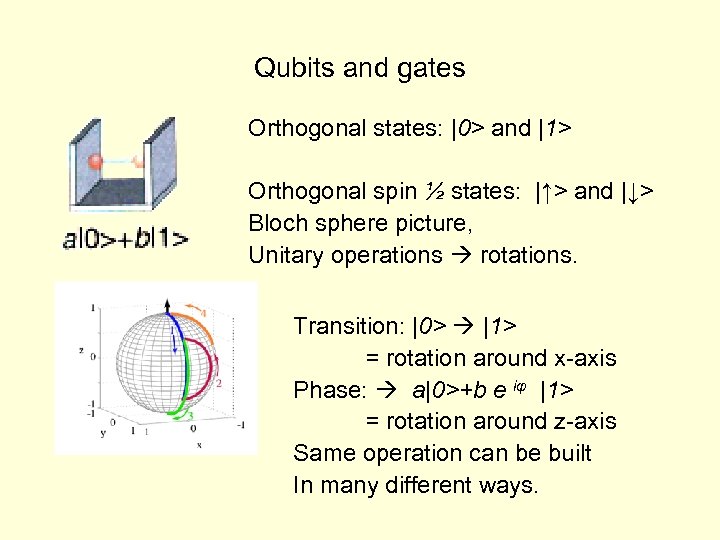
Qubits and gates Orthogonal states: |0> and |1> Orthogonal spin ½ states: |↑> and |↓> Bloch sphere picture, Unitary operations rotations. Transition: |0> |1> = rotation around x-axis Phase: a|0>+b e iφ |1> = rotation around z-axis Same operation can be built In many different ways.

Basic building blocks |0>+|1> |0> - |1> H 2 = NOT (cannot do that classically): Hadamard gate: |0> |1> |0> Phase gate: |0>, |1> e iφ|1>. π/8 gate (T-gate): |1> e i π/4 |1>. T and H do not commute: they span all rotations! C-Phase/C-NOT: same operations, but only carried out of ”control-qubit” is in state |0>.

Universality Classical computing: Gate alphabet, that allows computation of any function (fan-out + NAND). Surprising facts: Hadamard, π/8 gate and C-NOT is quantum universal. i. e. this set allows construction of any unitary operation on full register. (operating on any qubit and qubit pair). Hadamard, NOT and C-NOT gives no advantage for QC. We do not know which quantum property is needed for QC.

Quantum Error correction (Steane and Shor) • Errors happen. Can we detect and correct them ? • Classical approach: use copies and ”vote”: 0 000, 1 111, error: 001 000 by majority. • In QM, copying is forbidden, and checking by measurements collapse superposition states a|0>+b|1> 0> or |1> • Solution: a small algorithm |0> |000>, |1 |111> 00: OK 01: NOT_3 10: NOT_2 11: NOT_1: AARHUS UNIVERSITET

Quantum Error correction (Steane and Shor) • Errors happen. Can we detect and correct them ? • Classical approach: use copies and ”vote”: 0 000, 1 111, error: 001 000 by majority. • In QM, copying is forbidden, and checking by measurements collapse superposition states a|0>+b|1> 0> or |1> 5 -bit code can correct one flip or phase error multi-bit codes, topological states, gapped states AARHUS UNIVERSITET
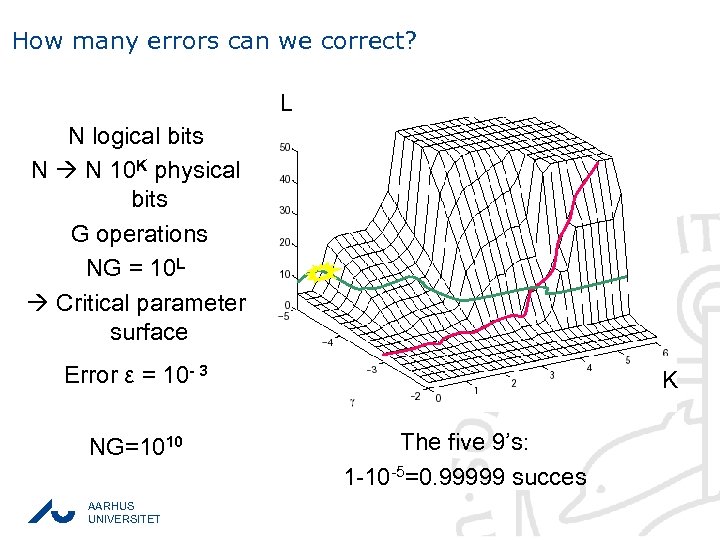
How many errors can we correct? L N logical bits N N 10 K physical bits G operations NG = 10 L Critical parameter surface Error ε = 10 - 3 NG=1010 AARHUS UNIVERSITET K The five 9’s: 1 -10 -5=0. 99999 succes
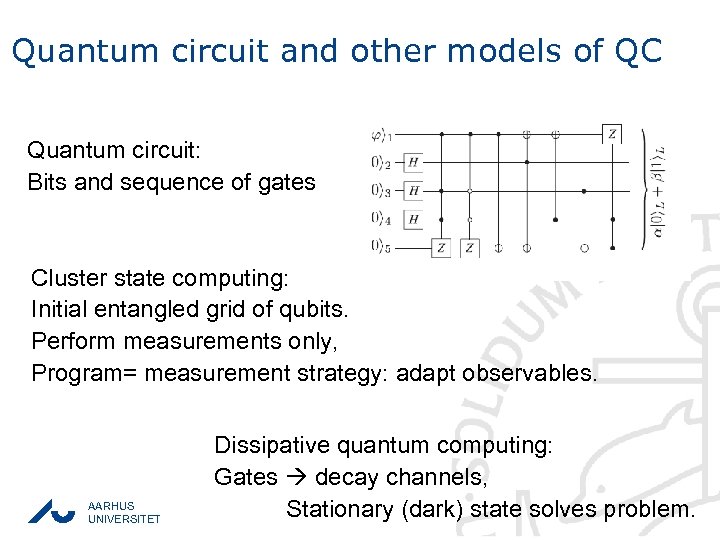
Quantum circuit and other models of QC Quantum circuit: Bits and sequence of gates Cluster state computing: Initial entangled grid of qubits. Perform measurements only, Program= measurement strategy: adapt observables. AARHUS UNIVERSITET Dissipative quantum computing: Gates decay channels, Stationary (dark) state solves problem.

QC is a great theoretical idea … … but it only works if we build one. AARHUS UNIVERSITET
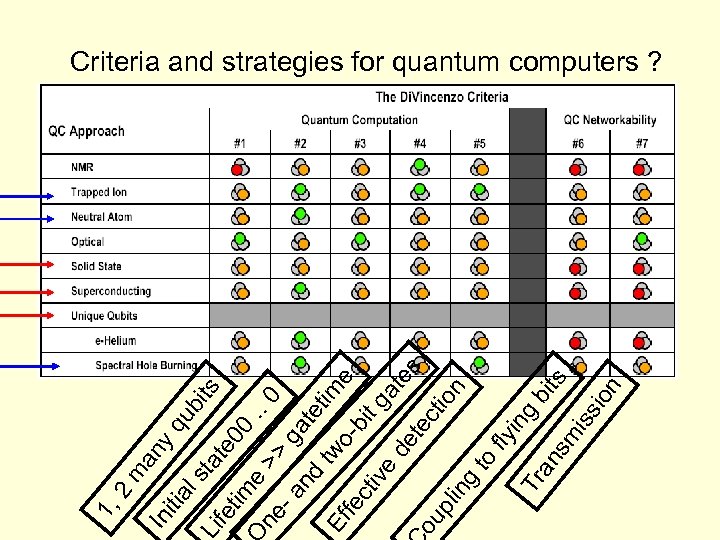
tim 00 te ta ub its yq ne e >>. . 0 -a g nd ate tim tw Ef e ofe bi ct tg ive at de es te ou ct io pl n in g to fly in g Tr bi an ts sm iss ion ife an m ls itia In 1, 2 Criteria and strategies for quantum computers ?

Carles Babbage (1792 -1871) on atoms: ”…. Every atom, impressed with good and with ill, retains at once the motions which philosophers and sages have imparted to it, mixed and combined in ten thousand ways with all that is worthless and base. ” Charles Babbage, Ninth Bridgewater Thesis, (1837).
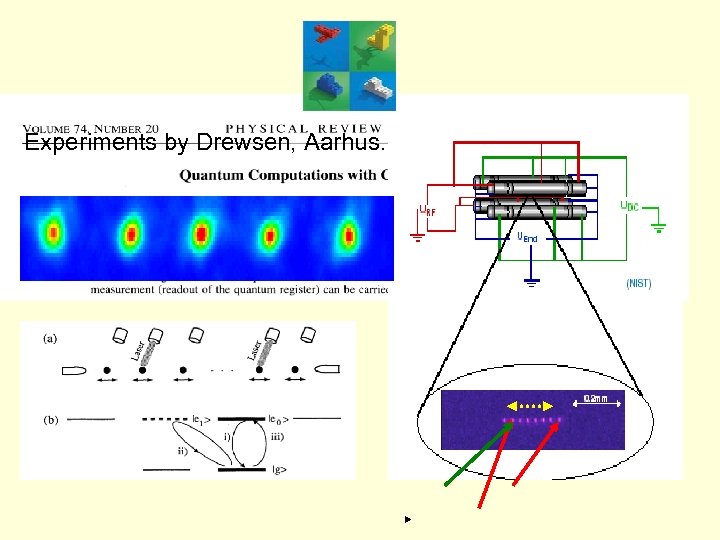
Experiments by Drewsen, Aarhus.
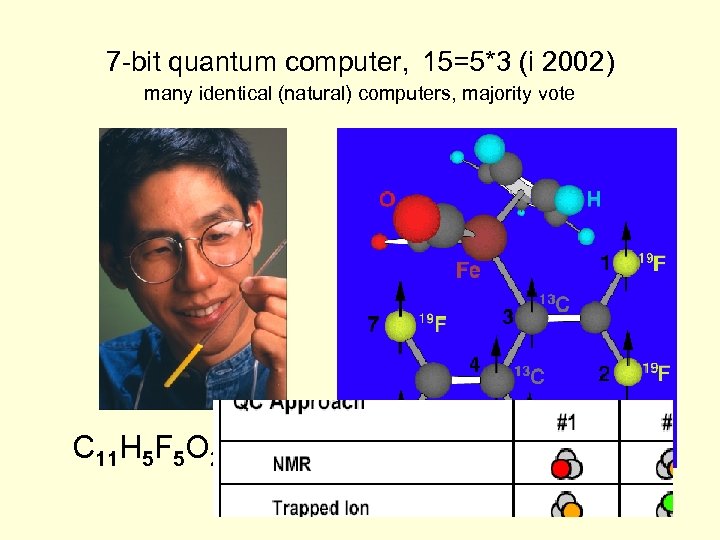
7 -bit quantum computer, 15=5*3 (i 2002) many identical (natural) computers, majority vote C 11 H 5 F 5 O 2 Fe
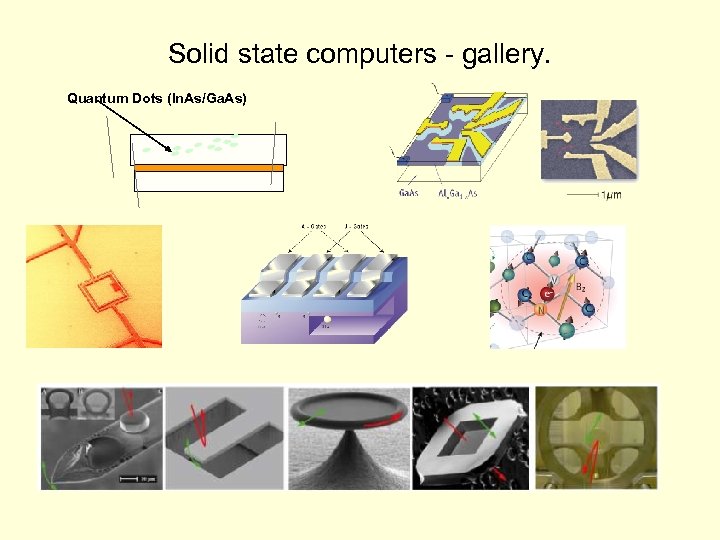
Solid state computers - gallery. Quantum Dots (In. As/Ga. As)

Atom chips
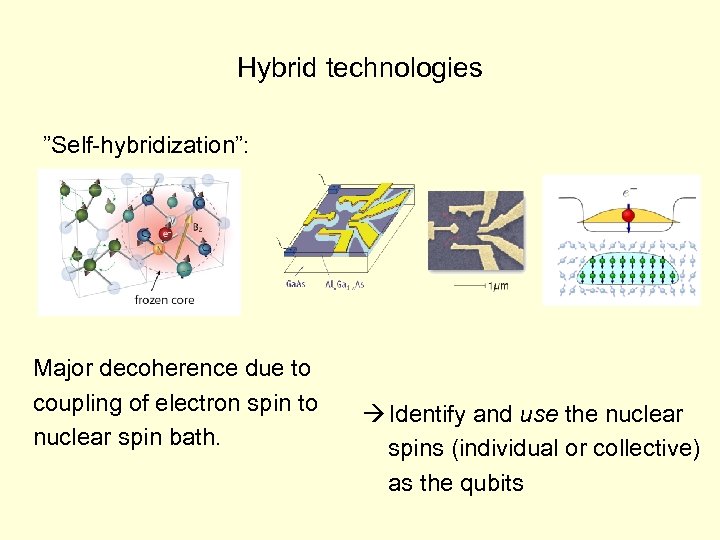
Hybrid technologies ”Self-hybridization”: Major decoherence due to coupling of electron spin to nuclear spin bath. Identify and use the nuclear spins (individual or collective) as the qubits
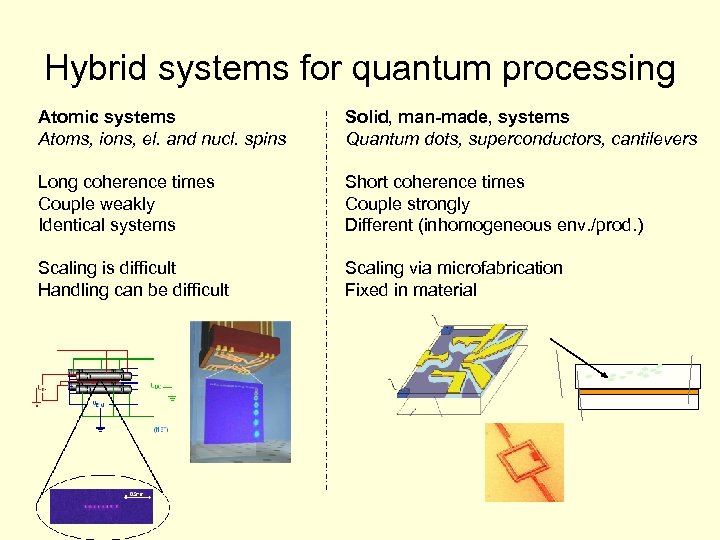
Hybrid systems for quantum processing Atomic systems Atoms, ions, el. and nucl. spins Solid, man-made, systems Quantum dots, superconductors, cantilevers Long coherence times Couple weakly Identical systems Short coherence times Couple strongly Different (inhomogeneous env. /prod. ) Scaling is difficult Handling can be difficult Scaling via microfabrication Fixed in material
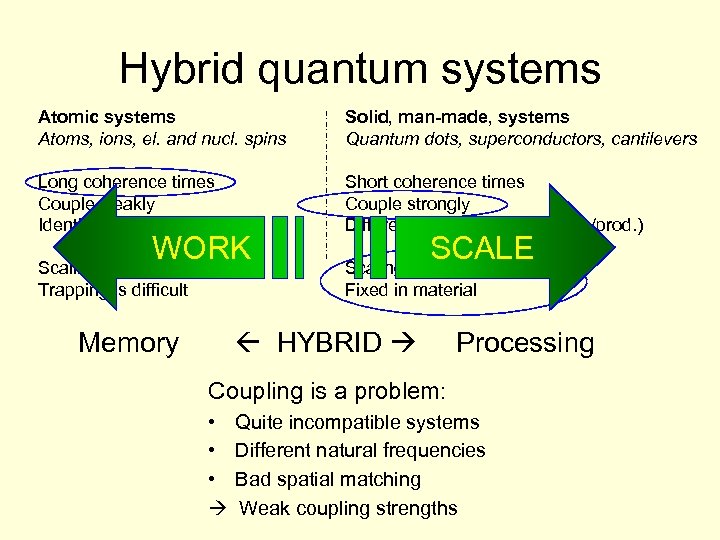
Hybrid quantum systems Atomic systems Atoms, ions, el. and nucl. spins Solid, man-made, systems Quantum dots, superconductors, cantilevers Long coherence times Couple weakly Identical systems Short coherence times Couple strongly Different (inhomogeneous env. /prod. ) Trapping is difficult Fixed in material WORK Scaling is difficult Memory SCALE Scaling via microfabrication HYBRID Processing Coupling is a problem: • • • Quite incompatible systems Different natural frequencies Bad spatial matching Weak coupling strengths
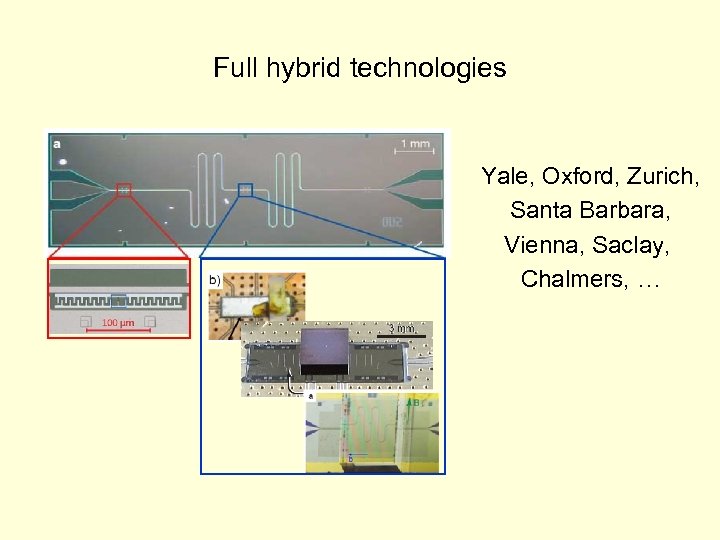
Full hybrid technologies Yale, Oxford, Zurich, Santa Barbara, Vienna, Saclay, Chalmers, …

And what if we fail completely… Niels Bohr (about Quantum Mechanics): ” … if we should one day wake up, and realize that it had all been only a dream, then I am absolutely convinced that we would still have learned something !”
2686f5c632a5dcaae113b0969a625846.ppt