afd422b069e01546cb24caafaf4d30b1.ppt
- Количество слайдов: 67
 Quantum Communication Nicolas Gisin GAP-Optique, University of Geneva S. Fasel, J. -D. Gautier, Ivan Marcikic, G. Ribordy, H. de Riedmatten, V. Scarani, A. Stefanov, D. Stücki, S. Tanzilli, W. Tittel, H. Zbinden § Quantum cryptography: a beautiful idea! § Quantum cryptography on a “black-board” GAP Optique § Quantum cryptography below lake Geneva § Quantum cryptography on noisy channels § Quantum teleportation § quantum memories 1
Quantum Communication Nicolas Gisin GAP-Optique, University of Geneva S. Fasel, J. -D. Gautier, Ivan Marcikic, G. Ribordy, H. de Riedmatten, V. Scarani, A. Stefanov, D. Stücki, S. Tanzilli, W. Tittel, H. Zbinden § Quantum cryptography: a beautiful idea! § Quantum cryptography on a “black-board” GAP Optique § Quantum cryptography below lake Geneva § Quantum cryptography on noisy channels § Quantum teleportation § quantum memories 1
 What is quantum communication § Quantum Communication is the art of transferring a quantum state from one location, Alice, to a distant one, Bob. GAP Optique Alice Bob § A quantum state can’t be copied, hence the original is necessarily destroyed and there remains no copy. § Copying quantum states would violate both Heisenberg’s uncertainty relations and the impossibility of faster than light signalling. Hence, the impossibility of “Q cloning” is one of the best established facts in Science. 2
What is quantum communication § Quantum Communication is the art of transferring a quantum state from one location, Alice, to a distant one, Bob. GAP Optique Alice Bob § A quantum state can’t be copied, hence the original is necessarily destroyed and there remains no copy. § Copying quantum states would violate both Heisenberg’s uncertainty relations and the impossibility of faster than light signalling. Hence, the impossibility of “Q cloning” is one of the best established facts in Science. 2
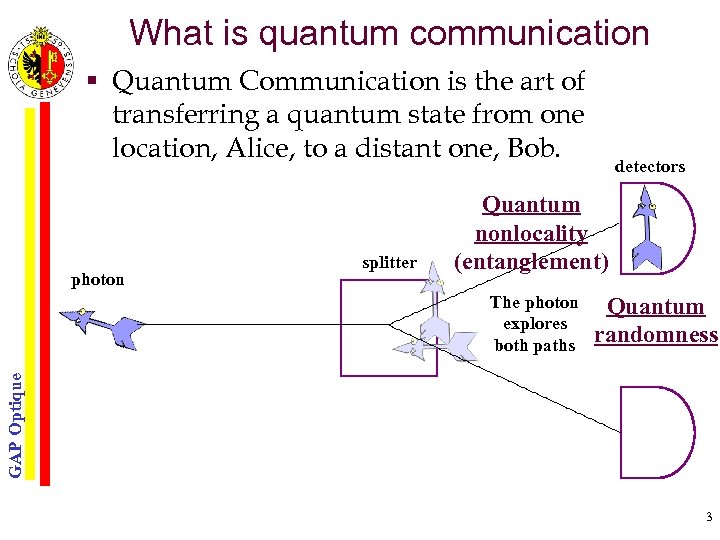 What is quantum communication § Quantum Communication is the art of transferring a quantum state from one location, Alice, to a distant one, Bob. photon splitter detectors Quantum nonlocality (entanglement) Quantum randomness GAP Optique The photon explores both paths 3
What is quantum communication § Quantum Communication is the art of transferring a quantum state from one location, Alice, to a distant one, Bob. photon splitter detectors Quantum nonlocality (entanglement) Quantum randomness GAP Optique The photon explores both paths 3
 Quantum cryptography: a beautiful idea • Basic Quantum Mechanics: • A quantum measurement perturbs the system QM limitations GAP Optique • However, QM gave us the laser, microelectronics, superconductivity, etc. • New Idea: Let's exploit QM for secure communications 4
Quantum cryptography: a beautiful idea • Basic Quantum Mechanics: • A quantum measurement perturbs the system QM limitations GAP Optique • However, QM gave us the laser, microelectronics, superconductivity, etc. • New Idea: Let's exploit QM for secure communications 4
 § If Eve tries to eavesdrop a "quantum communication channel", she has to perform some measurements on individual quanta (single photon pulses). GAP Optique § But, quantum mechanics tells us: every measurement perturbs the quantum system. § Hence the "reading" of the "quantum signal" by a third party reduces the correlation between Alice's and Bob's data. § Alice and Bob can thus detect any undesired third party by comparing (on a public channel) part of their "quantum signal". 5
§ If Eve tries to eavesdrop a "quantum communication channel", she has to perform some measurements on individual quanta (single photon pulses). GAP Optique § But, quantum mechanics tells us: every measurement perturbs the quantum system. § Hence the "reading" of the "quantum signal" by a third party reduces the correlation between Alice's and Bob's data. § Alice and Bob can thus detect any undesired third party by comparing (on a public channel) part of their "quantum signal". 5
 § The "quantum communication channel" is not used to transmit a message (information), only a "key" is transmitted (no information). § If it turns out that the key is corrupted, they simply disregard this key (no information is lost). GAP Optique § If the key passes successfully the control, Alice and Bob can use it safely. § Confidentiality of the key is checked before the message is send. § The safety of Quantum Cryptography is based on the root of Quantum Physics. 6
§ The "quantum communication channel" is not used to transmit a message (information), only a "key" is transmitted (no information). § If it turns out that the key is corrupted, they simply disregard this key (no information is lost). GAP Optique § If the key passes successfully the control, Alice and Bob can use it safely. § Confidentiality of the key is checked before the message is send. § The safety of Quantum Cryptography is based on the root of Quantum Physics. 6
 Modern Cryptology Secrecy is based on: Information theory The key is secrete The public key contains the decoding key, but it is very difficult to find (one way functions) GAP Optique Complexity theory The key is public The key contains the decoding key: Only the two partners have a copy ! The security is not proven (no one knows whether one way functions exist) Example: 127 x 229 = 29083 The security is proven (Shannon theorem) Example: Message: 011001001 Key: 110100110 Coded message: 101101111 7
Modern Cryptology Secrecy is based on: Information theory The key is secrete The public key contains the decoding key, but it is very difficult to find (one way functions) GAP Optique Complexity theory The key is public The key contains the decoding key: Only the two partners have a copy ! The security is not proven (no one knows whether one way functions exist) Example: 127 x 229 = 29083 The security is proven (Shannon theorem) Example: Message: 011001001 Key: 110100110 Coded message: 101101111 7
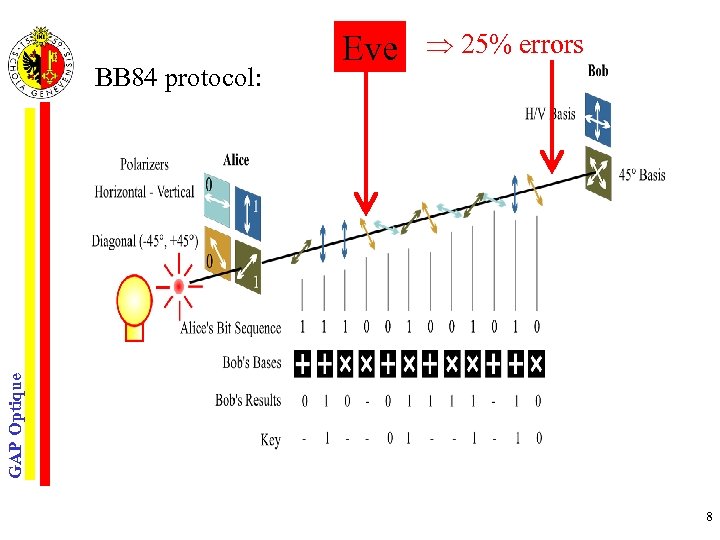 25% errors GAP Optique BB 84 protocol: Eve 8
25% errors GAP Optique BB 84 protocol: Eve 8
 9 GAP Optique
9 GAP Optique
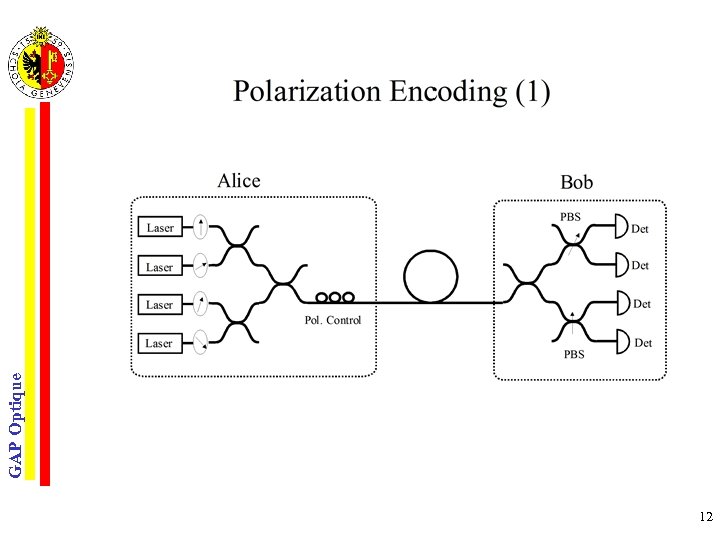
 Experimental Realization § Single photon source • laser pulses strongly attenuated ( 0. 1 photon/pulse) • photon pair source (parametric downconversion) • true single-photon source GAP Optique § Polarization or phase control during the single photon propagation • parallel transport of the polarization state (Berry topological phase) no vibrations • fluctuations of the birefringence thermal and mechanical stability • depolarization mode dispersion smaller than the source coherence • Stability of the interferometers coding for the phase § Single photon detection • avalanche photodiode (Germanium or In. Ga. As) in Geiger mode dark counts • based on supraconductors requires cryostats 10
Experimental Realization § Single photon source • laser pulses strongly attenuated ( 0. 1 photon/pulse) • photon pair source (parametric downconversion) • true single-photon source GAP Optique § Polarization or phase control during the single photon propagation • parallel transport of the polarization state (Berry topological phase) no vibrations • fluctuations of the birefringence thermal and mechanical stability • depolarization mode dispersion smaller than the source coherence • Stability of the interferometers coding for the phase § Single photon detection • avalanche photodiode (Germanium or In. Ga. As) in Geiger mode dark counts • based on supraconductors requires cryostats 10
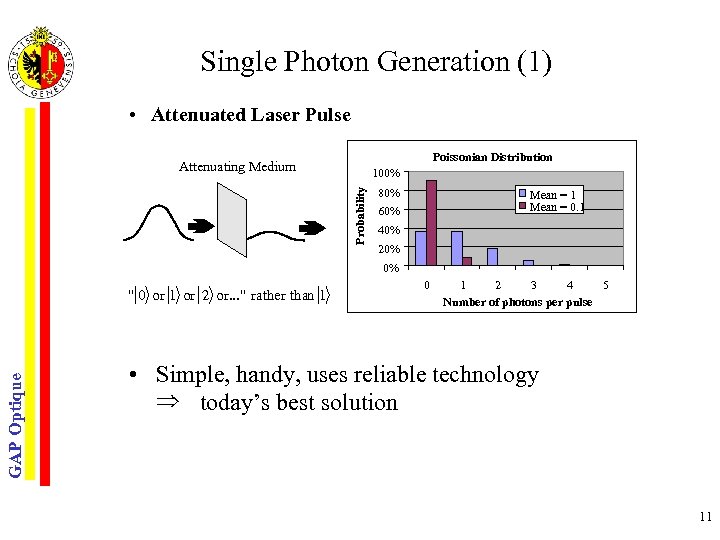 Single Photon Generation (1) • Attenuated Laser Pulse Poissonian Distribution Attenuating Medium Probability 100% 80% Mean = 1 Mean = 0. 1 60% 40% 20% 0% GAP Optique " 0 or 1 or 2 or. . . " rather than 1 0 1 2 3 4 5 Number of photons per pulse • Simple, handy, uses reliable technology today’s best solution 11
Single Photon Generation (1) • Attenuated Laser Pulse Poissonian Distribution Attenuating Medium Probability 100% 80% Mean = 1 Mean = 0. 1 60% 40% 20% 0% GAP Optique " 0 or 1 or 2 or. . . " rather than 1 0 1 2 3 4 5 Number of photons per pulse • Simple, handy, uses reliable technology today’s best solution 11
 12 GAP Optique
12 GAP Optique
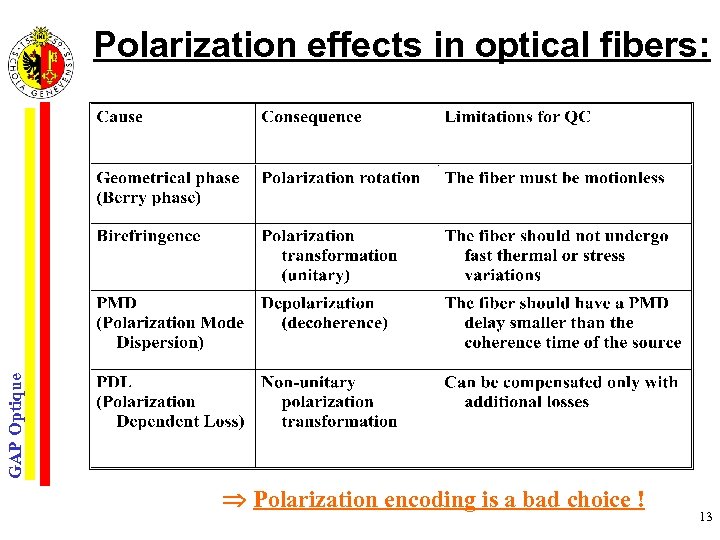 GAP Optique Polarization effects in optical fibers: Polarization encoding is a bad choice ! 13
GAP Optique Polarization effects in optical fibers: Polarization encoding is a bad choice ! 13
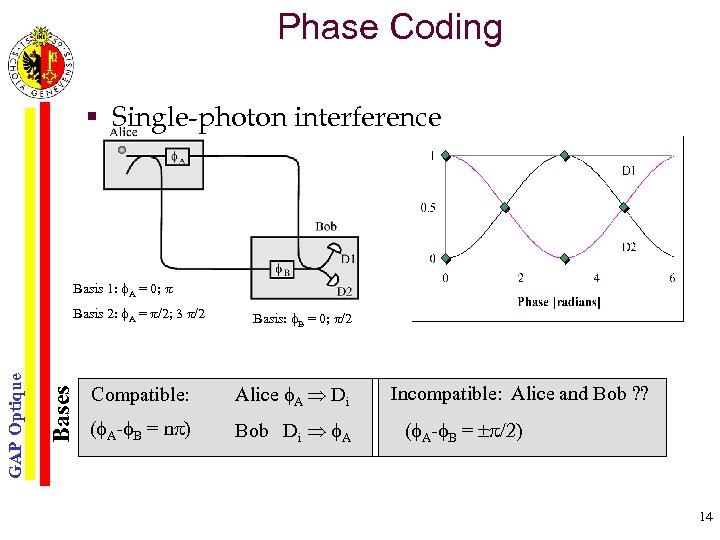 Phase Coding § Single-photon interference Basis 1: f. A = 0; p Bases GAP Optique Basis 2: f. A = p/2; 3 p/2 Basis: f. B = 0; p/2 Compatible: Alice f. A Di (f. A-f. B = np) Bob Di f. A Incompatible: Alice and Bob ? ? (f. A-f. B = p/2) 14
Phase Coding § Single-photon interference Basis 1: f. A = 0; p Bases GAP Optique Basis 2: f. A = p/2; 3 p/2 Basis: f. B = 0; p/2 Compatible: Alice f. A Di (f. A-f. B = np) Bob Di f. A Incompatible: Alice and Bob ? ? (f. A-f. B = p/2) 14
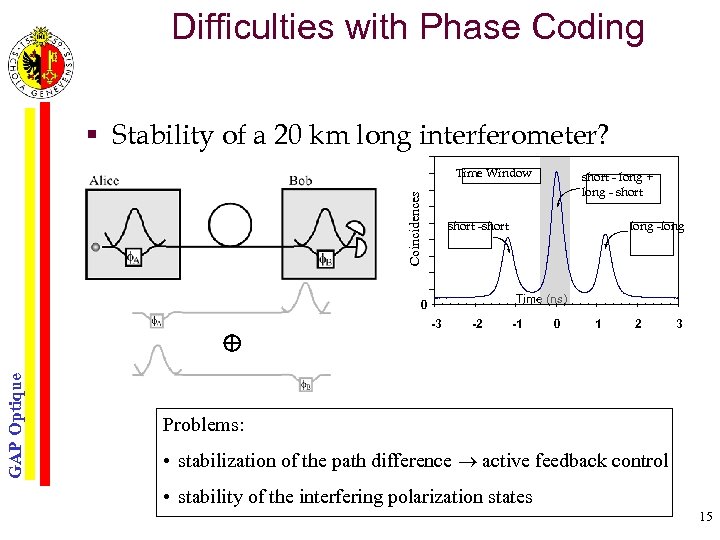 Difficulties with Phase Coding § Stability of a 20 km long interferometer? Coincidences Time Window GAP Optique long -long short -short Time (ns) 0 short - long + long - short -3 -2 -1 0 1 2 3 Problems: • stabilization of the path difference active feedback control • stability of the interfering polarization states 15
Difficulties with Phase Coding § Stability of a 20 km long interferometer? Coincidences Time Window GAP Optique long -long short -short Time (ns) 0 short - long + long - short -3 -2 -1 0 1 2 3 Problems: • stabilization of the path difference active feedback control • stability of the interfering polarization states 15
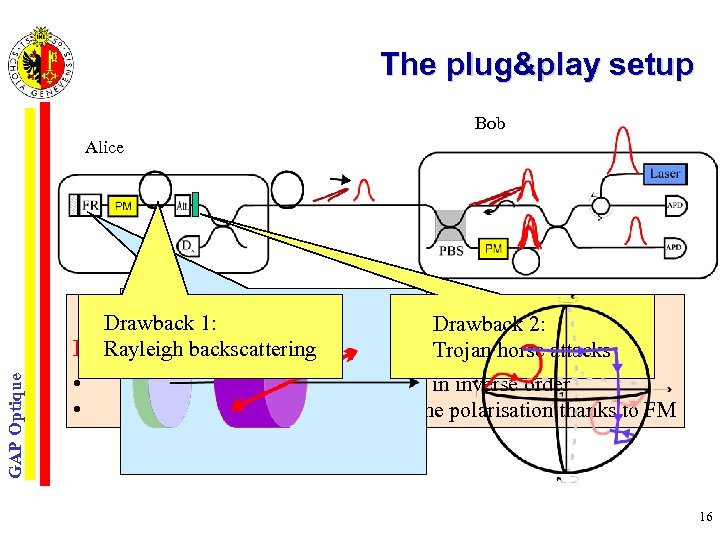 The plug&play setup Bob Alice GAP Optique Drawback 1: Drawback 2: Perfect interference (V 99%) without. Trojan horse attackssince: any adjustments, Rayleigh backscattering • • both pulses travel the same path in inverse order both pulses have exactly the same polarisation thanks to FM 16
The plug&play setup Bob Alice GAP Optique Drawback 1: Drawback 2: Perfect interference (V 99%) without. Trojan horse attackssince: any adjustments, Rayleigh backscattering • • both pulses travel the same path in inverse order both pulses have exactly the same polarisation thanks to FM 16
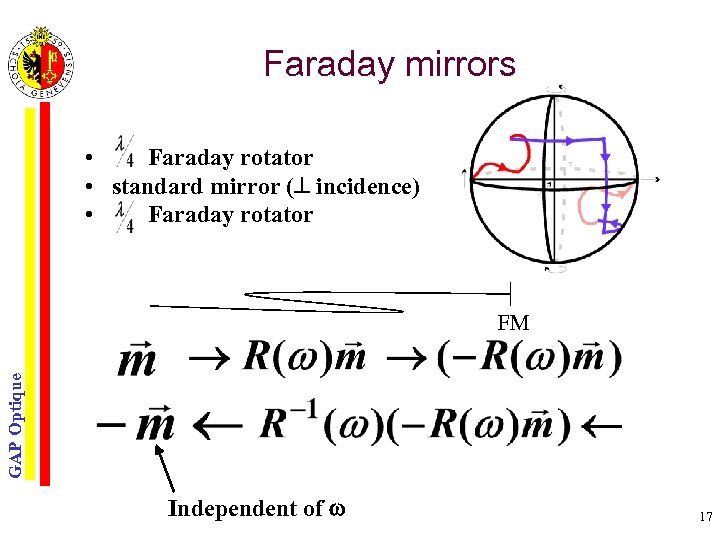 Faraday mirrors • Faraday rotator • standard mirror ( incidence) • Faraday rotator GAP Optique FM Independent of 17
Faraday mirrors • Faraday rotator • standard mirror ( incidence) • Faraday rotator GAP Optique FM Independent of 17
 Avalanche photodiodes § Single-photon detection with avalanches in Geiger mode GAP Optique macroscopic avalanche triggered by single-photon Silicon: 1000 nm Germanium: 1450 nm In. Ga. As/In. P: 1600 nm Typical value for In. Ga. As at -50 Co: =10%, D=10 -5 18
Avalanche photodiodes § Single-photon detection with avalanches in Geiger mode GAP Optique macroscopic avalanche triggered by single-photon Silicon: 1000 nm Germanium: 1450 nm In. Ga. As/In. P: 1600 nm Typical value for In. Ga. As at -50 Co: =10%, D=10 -5 18
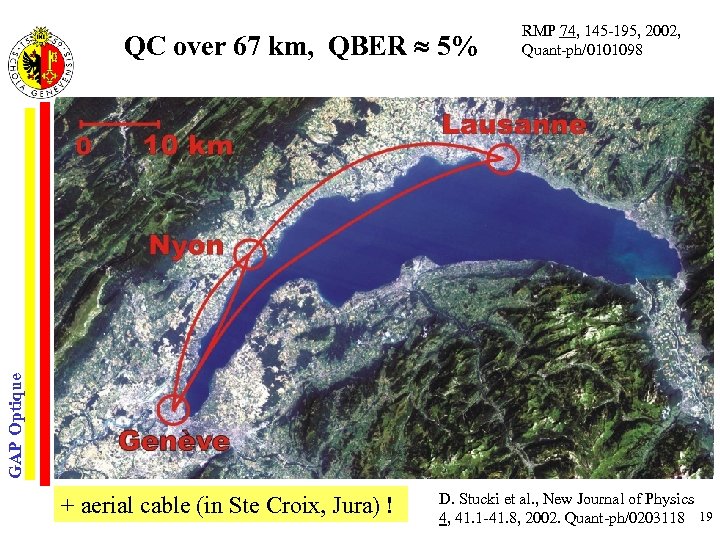 GAP Optique QC over 67 km, QBER 5% RMP 74, 145 -195, 2002, Quant-ph/0101098 + aerial cable (in Ste Croix, Jura) ! D. Stucki et al. , New Journal of Physics 4, 41. 1 -41. 8, 2002. Quant-ph/0203118 19
GAP Optique QC over 67 km, QBER 5% RMP 74, 145 -195, 2002, Quant-ph/0101098 + aerial cable (in Ste Croix, Jura) ! D. Stucki et al. , New Journal of Physics 4, 41. 1 -41. 8, 2002. Quant-ph/0203118 19
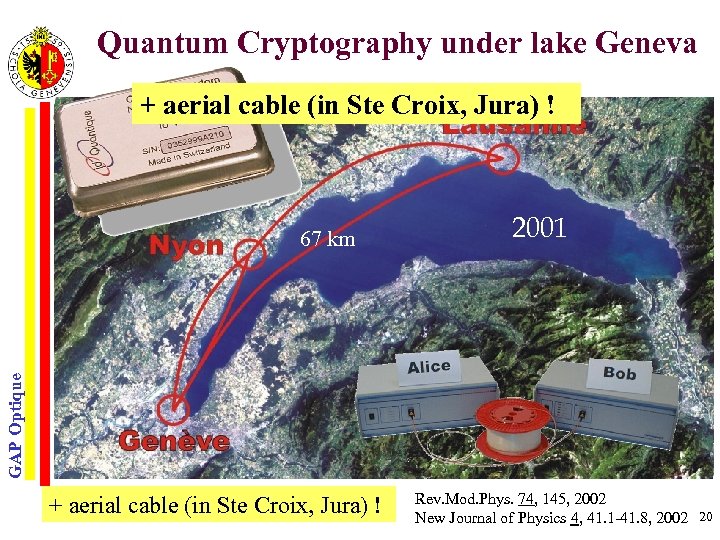 Quantum Cryptography under lake Geneva + aerial cable (in Ste Croix, Jura) ! 2001 GAP Optique 67 km + aerial cable (in Ste Croix, Jura) ! Rev. Mod. Phys. 74, 145, 2002 New Journal of Physics 4, 41. 1 -41. 8, 2002 20
Quantum Cryptography under lake Geneva + aerial cable (in Ste Croix, Jura) ! 2001 GAP Optique 67 km + aerial cable (in Ste Croix, Jura) ! Rev. Mod. Phys. 74, 145, 2002 New Journal of Physics 4, 41. 1 -41. 8, 2002 20
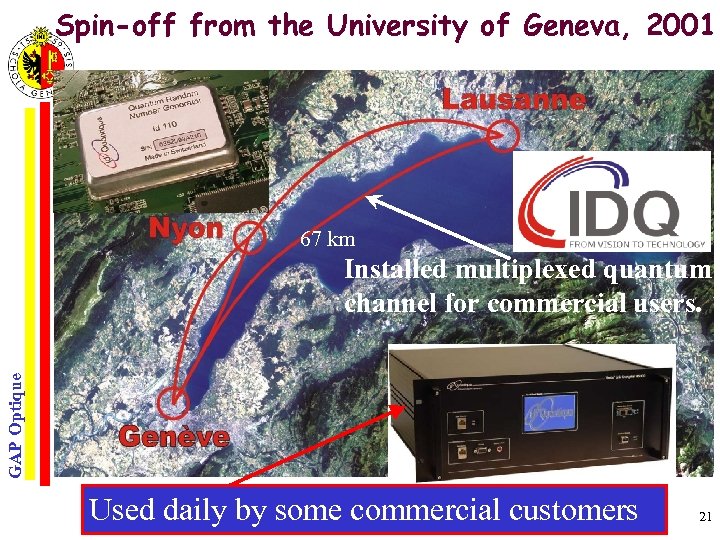 Spin-off from the University of Geneva, 2001 67 km GAP Optique Installed multiplexed quantum channel for commercial users. Used daily by some commercial customers 21
Spin-off from the University of Geneva, 2001 67 km GAP Optique Installed multiplexed quantum channel for commercial users. Used daily by some commercial customers 21
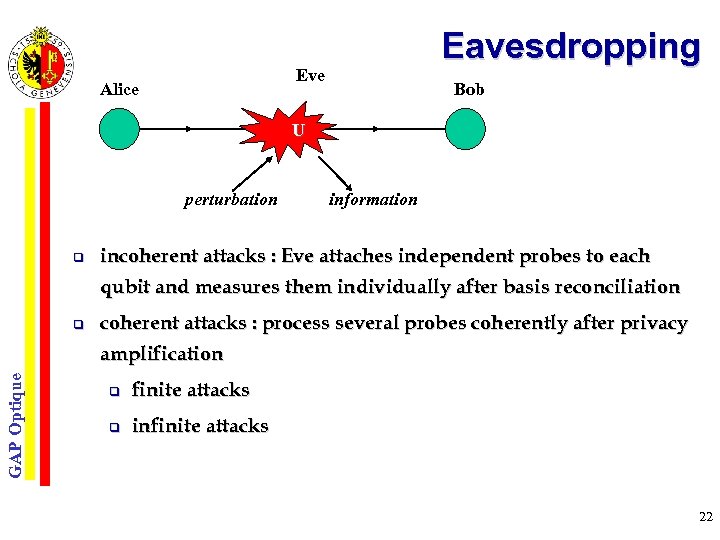 Eavesdropping Eve Alice Bob U perturbation q information incoherent attacks : Eve attaches independent probes to each qubit and measures them individually after basis reconciliation q coherent attacks : process several probes coherently after privacy GAP Optique amplification q finite attacks q infinite attacks 22
Eavesdropping Eve Alice Bob U perturbation q information incoherent attacks : Eve attaches independent probes to each qubit and measures them individually after basis reconciliation q coherent attacks : process several probes coherently after privacy GAP Optique amplification q finite attacks q infinite attacks 22
 Before using the key Alice and Bob must: § Evaluate QBER (Quantum Bit error Rate = Disturbance) § Apply a classical error correction protocol: GAP Optique e. g. compare bk+bn. If Alice and Bob agree, they keep bk and drop bn. If Alice and Bob disagree they drop both bits. § Apply a classical privacy amplification protocol: e. g. replace bk with bk+bn. Alice and Bob must evaluate how much information Eve may have ! 23
Before using the key Alice and Bob must: § Evaluate QBER (Quantum Bit error Rate = Disturbance) § Apply a classical error correction protocol: GAP Optique e. g. compare bk+bn. If Alice and Bob agree, they keep bk and drop bn. If Alice and Bob disagree they drop both bits. § Apply a classical privacy amplification protocol: e. g. replace bk with bk+bn. Alice and Bob must evaluate how much information Eve may have ! 23
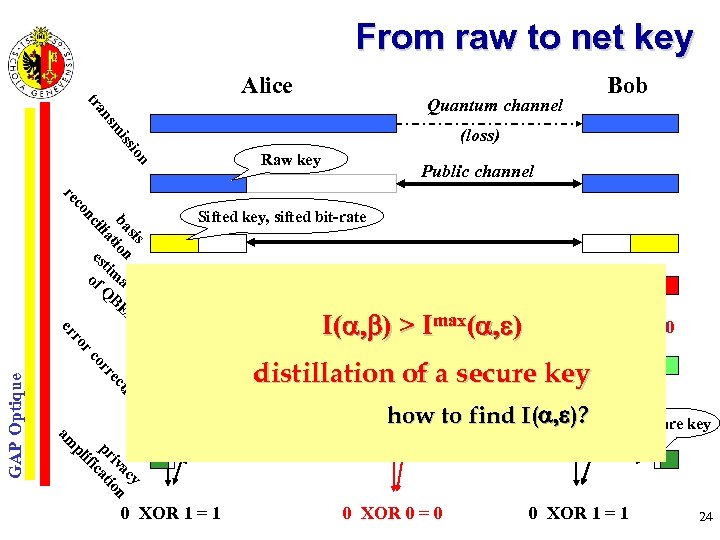 From raw to net key Alice Bob m ns tra Quantum channel ion iss (loss) Raw key Public channel sis ba tion a ili nc co re es tim of a Q tio BE n R Sifted key, sifted bit-rate 00100110 ct re n io 0– 1 secure key, net rate 0 00 how to find I(a, e)? – 1 secure key y ac iv on pr cati ifi pl am GAP Optique > Imax(a, e) XOR=1 distillation of a secure key Eve or rc ro er 0 1 1 0 0 1 1 1 XOR=1 a, b) I( XOR=0 XOR=1 0 XOR 1 = 1 0 XOR 0 = 0 0 XOR 1 = 1 24
From raw to net key Alice Bob m ns tra Quantum channel ion iss (loss) Raw key Public channel sis ba tion a ili nc co re es tim of a Q tio BE n R Sifted key, sifted bit-rate 00100110 ct re n io 0– 1 secure key, net rate 0 00 how to find I(a, e)? – 1 secure key y ac iv on pr cati ifi pl am GAP Optique > Imax(a, e) XOR=1 distillation of a secure key Eve or rc ro er 0 1 1 0 0 1 1 1 XOR=1 a, b) I( XOR=0 XOR=1 0 XOR 1 = 1 0 XOR 0 = 0 0 XOR 1 = 1 24
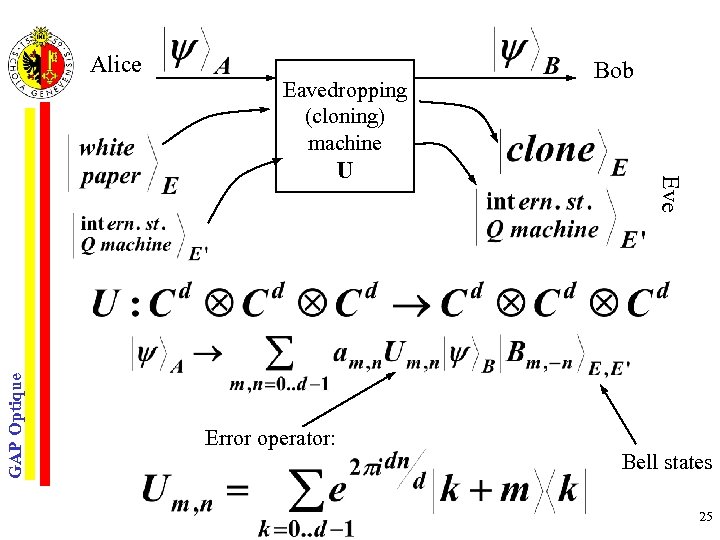 Alice Eavedropping (cloning) machine GAP Optique Error operator: Eve U Bob Bell states 25
Alice Eavedropping (cloning) machine GAP Optique Error operator: Eve U Bob Bell states 25
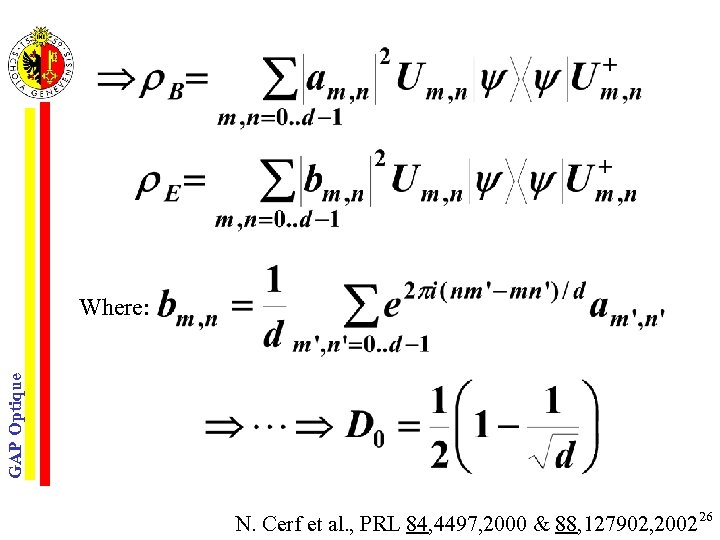 GAP Optique Where: N. Cerf et al. , PRL 84, 4497, 2000 & 88, 127902, 200226
GAP Optique Where: N. Cerf et al. , PRL 84, 4497, 2000 & 88, 127902, 200226
 individual, symmetrical attacks and BB’ 84 0. 8 classical error correction and privacy amplification 1. 0 Eve's information secret-key rate Information [bit] Individual/finite collective, symmetric attacks: 0. 6 QBERMax 15 % infinite collective attacks: QBERMax 11 % 0. 4 (lower bound) GAP Optique 0. 2 0. 0 Bob's information one way communication 0. 0 0. 1 0. 2 QBERmax Rnet=Rsifted (I (a, b) - Imax(a, e)) 0. 3 0. 4 0. 5 QBER (Disturbance) 27
individual, symmetrical attacks and BB’ 84 0. 8 classical error correction and privacy amplification 1. 0 Eve's information secret-key rate Information [bit] Individual/finite collective, symmetric attacks: 0. 6 QBERMax 15 % infinite collective attacks: QBERMax 11 % 0. 4 (lower bound) GAP Optique 0. 2 0. 0 Bob's information one way communication 0. 0 0. 1 0. 2 QBERmax Rnet=Rsifted (I (a, b) - Imax(a, e)) 0. 3 0. 4 0. 5 QBER (Disturbance) 27
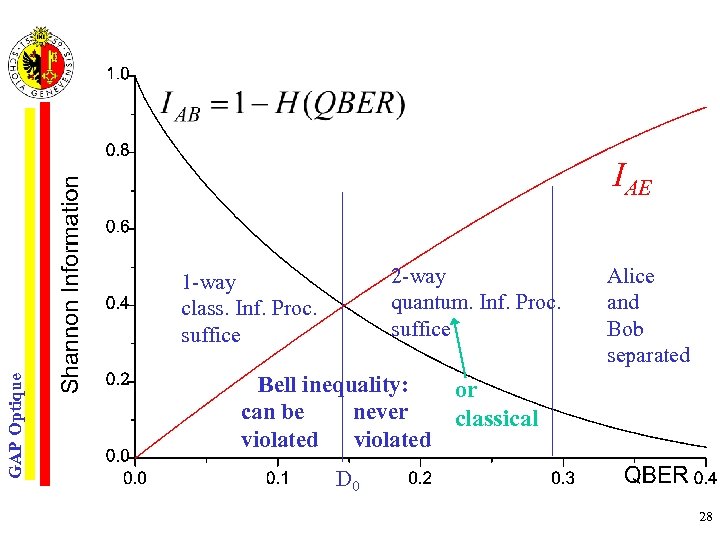 IAE 2 -way quantum. Inf. Proc. suffice GAP Optique 1 -way class. Inf. Proc. suffice Bell inequality: can be never violated Alice and Bob separated or classical D 0 28
IAE 2 -way quantum. Inf. Proc. suffice GAP Optique 1 -way class. Inf. Proc. suffice Bell inequality: can be never violated Alice and Bob separated or classical D 0 28
 29 GAP Optique
29 GAP Optique
 Quantum Hacking 1. There is nothing like “unconditional security” ! (as emphasized in our 2002 RMP) GAP Optique 2. But it should not obscure the fact that there is nothing like cracking QKD ! The principle of QKD will never be attacked, only the implementation. In contrast, in classical crypto both the principle and the implementation can be attacked. If the principle of classical crypto gets broken, then - All electronic money looses all value - All past communications can be read 30
Quantum Hacking 1. There is nothing like “unconditional security” ! (as emphasized in our 2002 RMP) GAP Optique 2. But it should not obscure the fact that there is nothing like cracking QKD ! The principle of QKD will never be attacked, only the implementation. In contrast, in classical crypto both the principle and the implementation can be attacked. If the principle of classical crypto gets broken, then - All electronic money looses all value - All past communications can be read 30
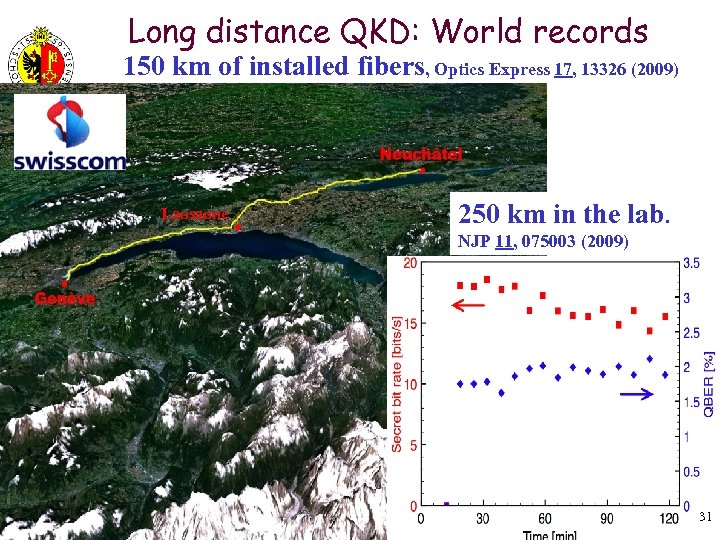 Long distance QKD: World records 150 km of installed fibers, Optics Express 17, 13326 (2009) Lausanne 250 km in the lab. GAP Optique NJP 11, 075003 (2009) 31
Long distance QKD: World records 150 km of installed fibers, Optics Express 17, 13326 (2009) Lausanne 250 km in the lab. GAP Optique NJP 11, 075003 (2009) 31
 How far can one send a photon ? Secret Rate Key Rate 10 MHz P 2 P + WDM +4 Years Today Lab 1 MHz Today Commercial 100 k. Hz 1 k. Hz GAP Optique 1 Hz 100 200 300 Distance [km] 400 There is a hard wall around 400 km ! With the best optical fibers, perfect noise-free detectors and ideal 10 GHz single-photon sources, it would take centuries to send 1 qubit over 1000 km ! 32
How far can one send a photon ? Secret Rate Key Rate 10 MHz P 2 P + WDM +4 Years Today Lab 1 MHz Today Commercial 100 k. Hz 1 k. Hz GAP Optique 1 Hz 100 200 300 Distance [km] 400 There is a hard wall around 400 km ! With the best optical fibers, perfect noise-free detectors and ideal 10 GHz single-photon sources, it would take centuries to send 1 qubit over 1000 km ! 32
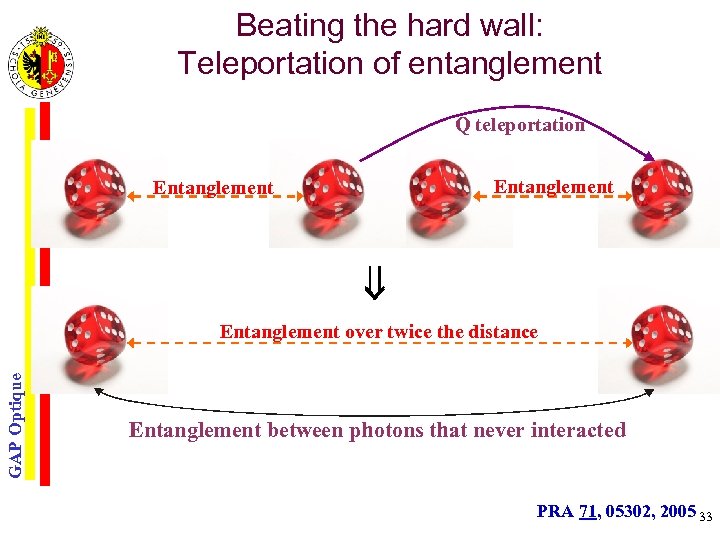 Beating the hard wall: Teleportation of entanglement Q teleportation Entanglement GAP Optique Entanglement over twice the distance Entanglement between photons that never interacted PRA 71, 05302, 2005 33
Beating the hard wall: Teleportation of entanglement Q teleportation Entanglement GAP Optique Entanglement over twice the distance Entanglement between photons that never interacted PRA 71, 05302, 2005 33
 The Geneva Teleportation experiment over 3 x 2 km Photon = particle (atom) of light Unpolarized photon ( unstructured dust) GAP Optique Polarized photon ( structured photon) 34
The Geneva Teleportation experiment over 3 x 2 km Photon = particle (atom) of light Unpolarized photon ( unstructured dust) GAP Optique Polarized photon ( structured photon) 34
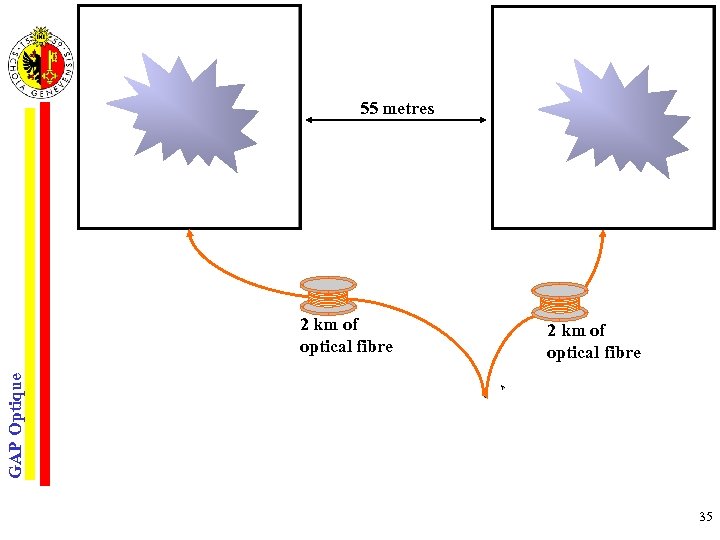 55 metres GAP Optique 2 km of optical fibre Two entangled photons 35
55 metres GAP Optique 2 km of optical fibre Two entangled photons 35
 55 metres GAP Optique 2 km of optical fibre 36
55 metres GAP Optique 2 km of optical fibre 36
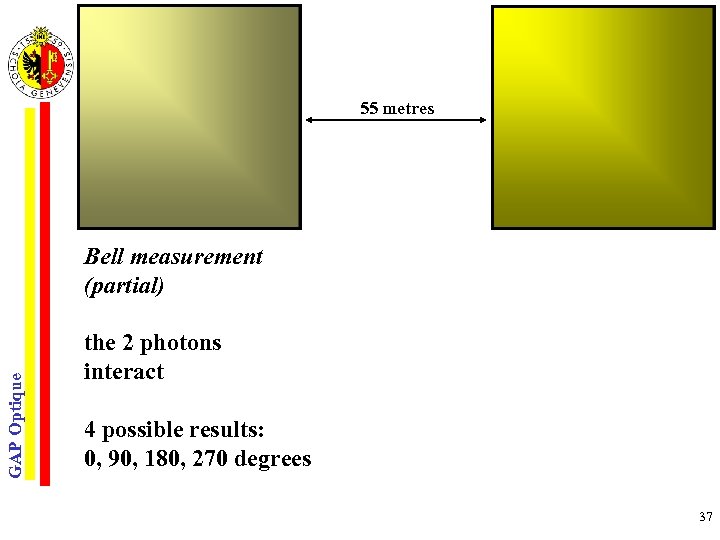 55 metres GAP Optique Bell measurement (partial) the 2 photons interact 4 possible results: 0, 90, 180, 270 degrees 37
55 metres GAP Optique Bell measurement (partial) the 2 photons interact 4 possible results: 0, 90, 180, 270 degrees 37
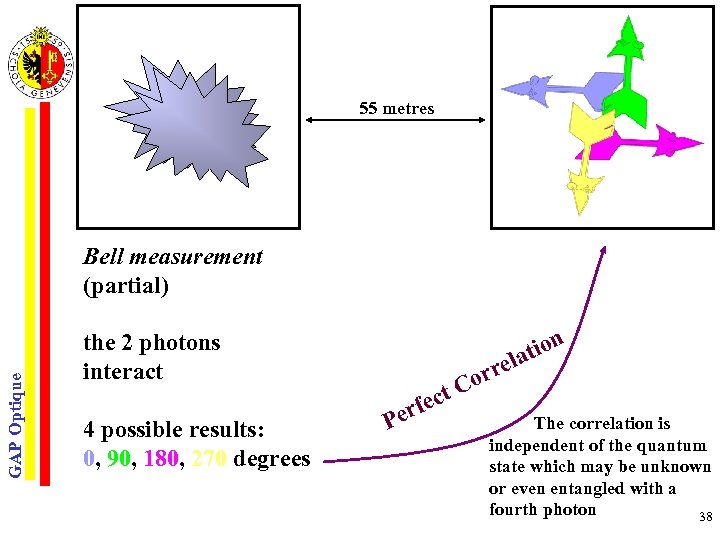 55 metres GAP Optique Bell measurement (partial) the 2 photons interact 4 possible results: 0, 90, 180, 270 degrees tion la e erf P e orr ct C The correlation is independent of the quantum state which may be unknown or even entangled with a fourth photon 38
55 metres GAP Optique Bell measurement (partial) the 2 photons interact 4 possible results: 0, 90, 180, 270 degrees tion la e erf P e orr ct C The correlation is independent of the quantum state which may be unknown or even entangled with a fourth photon 38
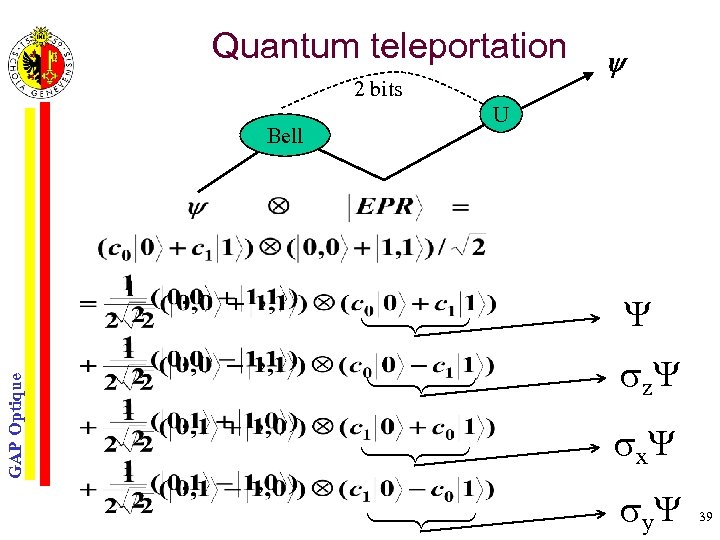 Quantum teleportation 2 bits U Bell GAP Optique z x y 39
Quantum teleportation 2 bits U Bell GAP Optique z x y 39
 What is teleported ? § According to Aristotle, objects are constituted by matter and form, ie by elementary particles and quantum states. GAP Optique § Matter and energy can not be teleported from one place to another: they can not be transferred from one place to another without passing through intermediate locations. § However, quantum states, the ultimate structure of objects, can be teleported. Accordingly, objects can be transferred from one place to another without ever existing anywhere in between! But only the structure is teleported, the matter stays at the source and has to be already present at the final location. 40
What is teleported ? § According to Aristotle, objects are constituted by matter and form, ie by elementary particles and quantum states. GAP Optique § Matter and energy can not be teleported from one place to another: they can not be transferred from one place to another without passing through intermediate locations. § However, quantum states, the ultimate structure of objects, can be teleported. Accordingly, objects can be transferred from one place to another without ever existing anywhere in between! But only the structure is teleported, the matter stays at the source and has to be already present at the final location. 40
 Implications of entanglement § The world can’t be understood in terms of “little billiard balls”. GAP Optique § The world is nonlocal (but the nonlocality can’t be used to signal faster than light). § Quantum physics offers new ways of processing information. 41
Implications of entanglement § The world can’t be understood in terms of “little billiard balls”. GAP Optique § The world is nonlocal (but the nonlocality can’t be used to signal faster than light). § Quantum physics offers new ways of processing information. 41
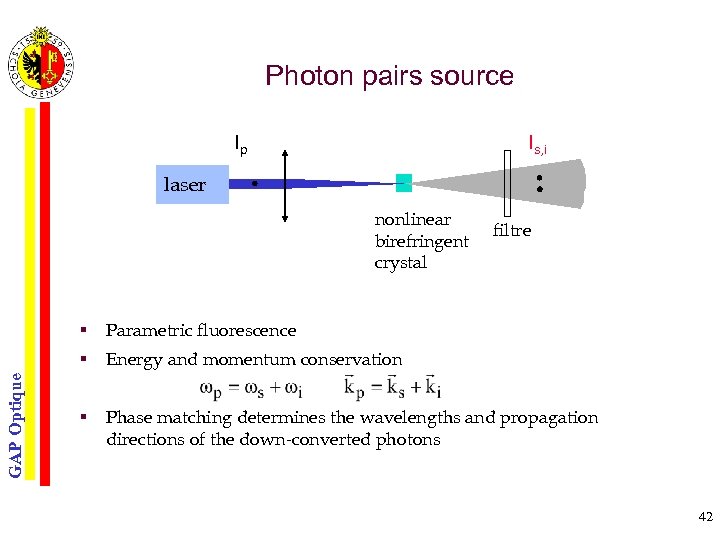 Photon pairs source lp ls, i laser nonlinear birefringent crystal filtre Parametric fluorescence § GAP Optique § Energy and momentum conservation § Phase matching determines the wavelengths and propagation directions of the down-converted photons 42
Photon pairs source lp ls, i laser nonlinear birefringent crystal filtre Parametric fluorescence § GAP Optique § Energy and momentum conservation § Phase matching determines the wavelengths and propagation directions of the down-converted photons 42
 GAP Optique 2 - source of Aspect’s 1982 experiment 43
GAP Optique 2 - source of Aspect’s 1982 experiment 43
 Photon pairs source (Geneva 1997) er as L nm 5 65 F L P KNb. O 3 § output 1 Energy-time entanglement output 2 § lens GAP Optique filter laser § simple, compact, handy § crystal diode laser 40 x 45 x 15 cm 3 § Ipump = 8 m. W § with waveguide in Li. Nb. O 3 with quasi phase matching, Ipump 8 W 44
Photon pairs source (Geneva 1997) er as L nm 5 65 F L P KNb. O 3 § output 1 Energy-time entanglement output 2 § lens GAP Optique filter laser § simple, compact, handy § crystal diode laser 40 x 45 x 15 cm 3 § Ipump = 8 m. W § with waveguide in Li. Nb. O 3 with quasi phase matching, Ipump 8 W 44
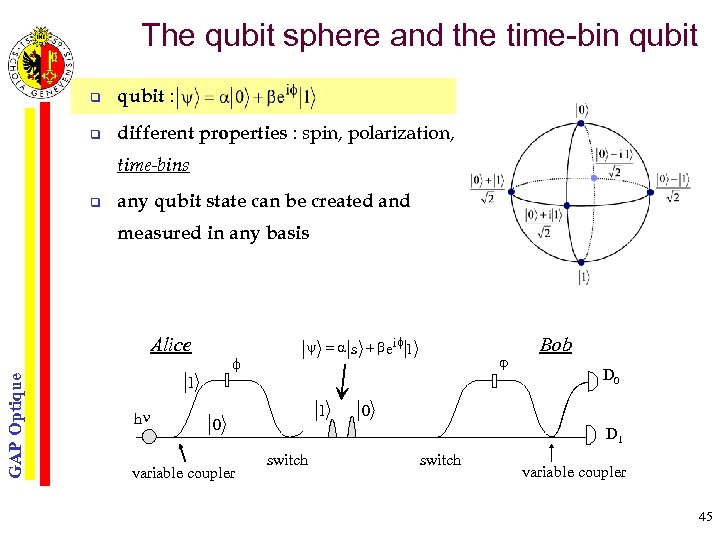 The qubit sphere and the time-bin qubit q qubit : q different properties : spin, polarization, time-bins q any qubit state can be created and measured in any basis GAP Optique Alice f y = a s + be if l j 1 hn 1 0 variable coupler Bob D 0 0 D 1 switch variable coupler 45
The qubit sphere and the time-bin qubit q qubit : q different properties : spin, polarization, time-bins q any qubit state can be created and measured in any basis GAP Optique Alice f y = a s + be if l j 1 hn 1 0 variable coupler Bob D 0 0 D 1 switch variable coupler 45
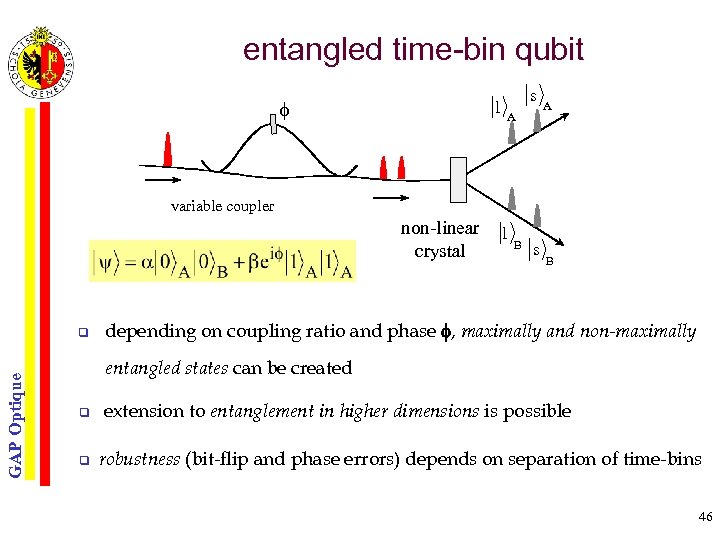 entangled time-bin qubit f l s A A variable coupler non-linear crystal GAP Optique q l B s B depending on coupling ratio and phase f, maximally and non-maximally entangled states can be created q q extension to entanglement in higher dimensions is possible robustness (bit-flip and phase errors) depends on separation of time-bins 46
entangled time-bin qubit f l s A A variable coupler non-linear crystal GAP Optique q l B s B depending on coupling ratio and phase f, maximally and non-maximally entangled states can be created q q extension to entanglement in higher dimensions is possible robustness (bit-flip and phase errors) depends on separation of time-bins 46
 2 -photon Q cryptography: Franson interferometer Two unbalanced interferometers no first order interferences photon pairs possibility to measure coincidences GAP Optique One can not distinguish between "long-long" and "short-short" Hence, according to QM, one should add the probability amplitudes interferences (of second order) 47
2 -photon Q cryptography: Franson interferometer Two unbalanced interferometers no first order interferences photon pairs possibility to measure coincidences GAP Optique One can not distinguish between "long-long" and "short-short" Hence, according to QM, one should add the probability amplitudes interferences (of second order) 47
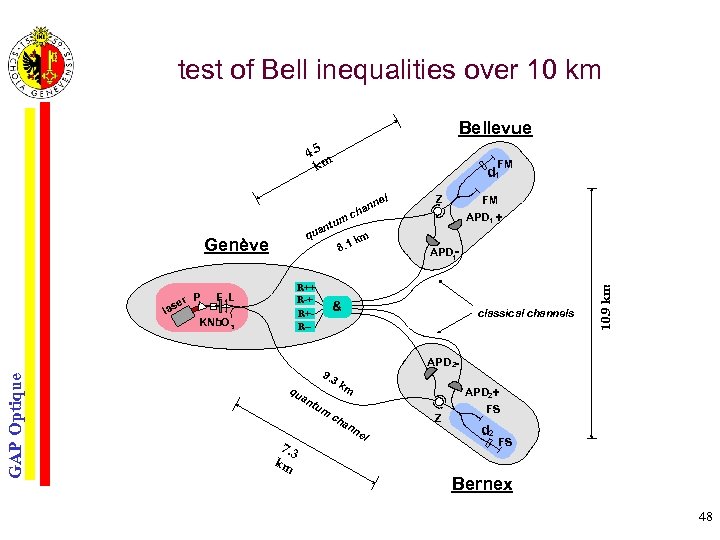 test of Bell inequalities over 10 km Bellevue 4. 5 km FM d 1 m ntu ua q km 8. 1 Genève er P GAP Optique las R++ R-+ R+R-- F L KNb. O 3 an APD 1 - tum classical channels APD 2 km ch APD 2+ an 7. 3 km FM APD 1 + & 9. 3 qu Z 10. 9 km el nn a ch ne Z l FS d 2 FS Bernex 48
test of Bell inequalities over 10 km Bellevue 4. 5 km FM d 1 m ntu ua q km 8. 1 Genève er P GAP Optique las R++ R-+ R+R-- F L KNb. O 3 an APD 1 - tum classical channels APD 2 km ch APD 2+ an 7. 3 km FM APD 1 + & 9. 3 qu Z 10. 9 km el nn a ch ne Z l FS d 2 FS Bernex 48
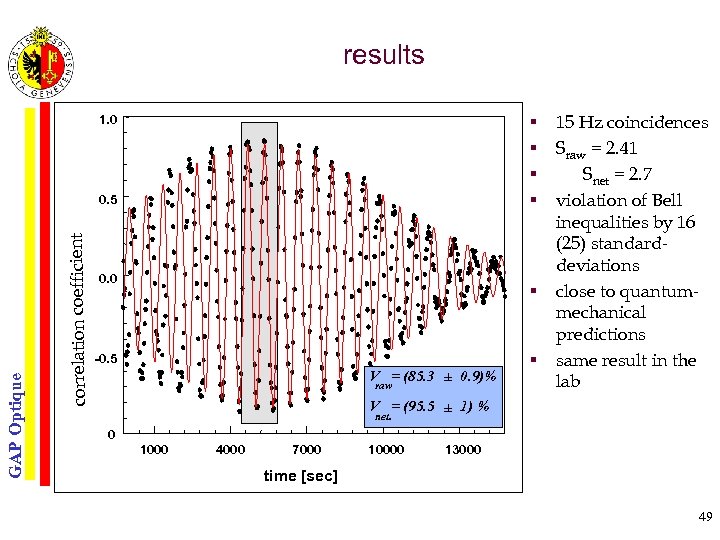 results § § 1. 0 correlation coefficient GAP Optique 0. 5 0. 0 § -0. 5 V = (85. 3 ± 0. 9)% raw § 15 Hz coincidences Sraw = 2. 41 Snet = 2. 7 violation of Bell inequalities by 16 (25) standarddeviations close to quantummechanical predictions same result in the lab V = (95. 5 ± 1) % net. 0 1000 4000 7000 10000 13000 time [sec] 49
results § § 1. 0 correlation coefficient GAP Optique 0. 5 0. 0 § -0. 5 V = (85. 3 ± 0. 9)% raw § 15 Hz coincidences Sraw = 2. 41 Snet = 2. 7 violation of Bell inequalities by 16 (25) standarddeviations close to quantummechanical predictions same result in the lab V = (95. 5 ± 1) % net. 0 1000 4000 7000 10000 13000 time [sec] 49
 GAP Optique le labo 50
GAP Optique le labo 50
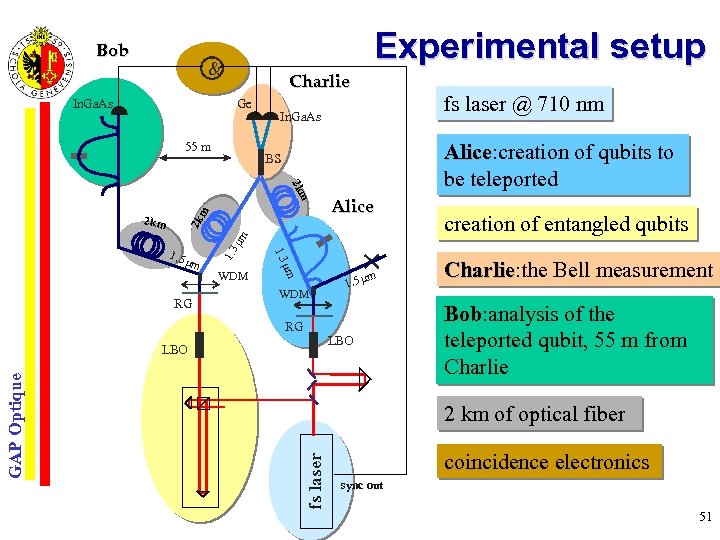 Bob Experimental setup & In. Ga. As Charlie Ge 55 m In. Ga. As Alice: creation of qubits to Alice be teleported BS m m 2 k Alice WDM RG m m 1. 3 1. 5 1. 3 m 2 k 2 km WDM RG creation of entangled qubits Charlie: the Bell measurement Charlie Bob: analysis of the Bob teleported qubit, 55 m from Charlie 2 km of optical fiber fs laser GAP Optique m 1. 5 LBO fs laser @ 710 nm coincidence electronics sync out 51
Bob Experimental setup & In. Ga. As Charlie Ge 55 m In. Ga. As Alice: creation of qubits to Alice be teleported BS m m 2 k Alice WDM RG m m 1. 3 1. 5 1. 3 m 2 k 2 km WDM RG creation of entangled qubits Charlie: the Bell measurement Charlie Bob: analysis of the Bob teleported qubit, 55 m from Charlie 2 km of optical fiber fs laser GAP Optique m 1. 5 LBO fs laser @ 710 nm coincidence electronics sync out 51
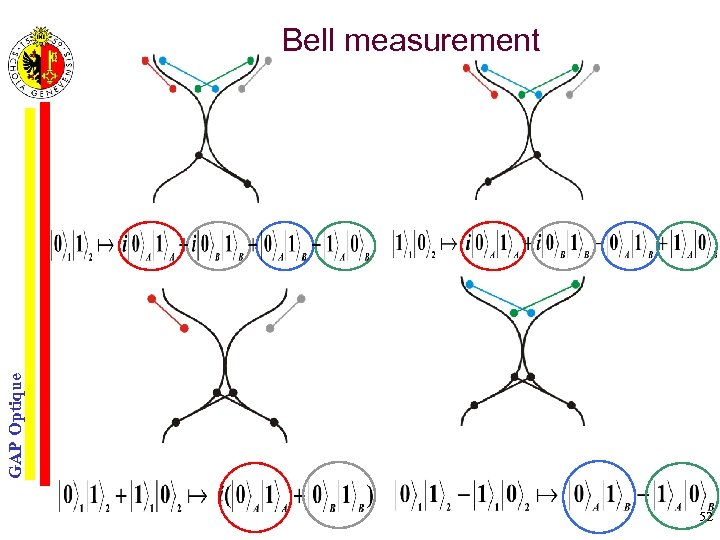 GAP Optique Bell measurement 52
GAP Optique Bell measurement 52
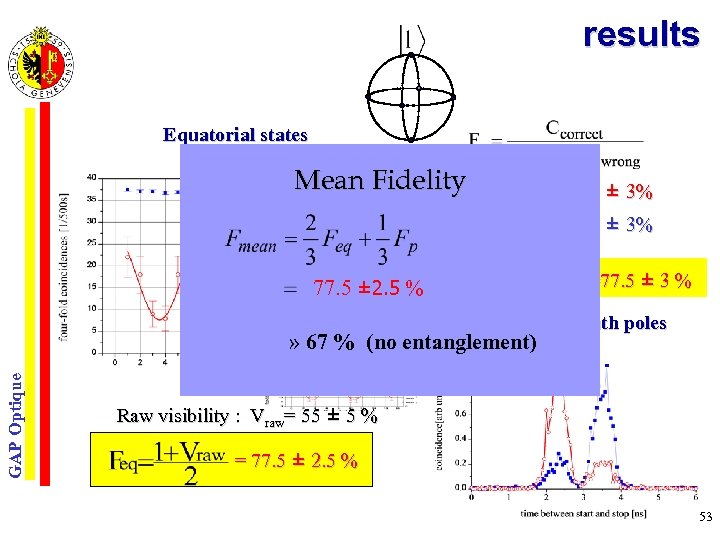 results Equatorial states Mean Fidelity = 78 ± 3% = 77 ± 3% 77. 5 ± 2. 5 % mean fidelity: Fpoles=77. 5 ± 3 % North & south poles GAP Optique » 67 % (no entanglement) Raw visibility : Vraw= 55 ± 5 % = 77. 5 ± 2. 5 % 53
results Equatorial states Mean Fidelity = 78 ± 3% = 77 ± 3% 77. 5 ± 2. 5 % mean fidelity: Fpoles=77. 5 ± 3 % North & south poles GAP Optique » 67 % (no entanglement) Raw visibility : Vraw= 55 ± 5 % = 77. 5 ± 2. 5 % 53
 Requirements for Quantum Repeaters GAP Optique 1. Distribution of entanglement over long distances 2. Multi-mode quantum memories 3. Entanglement swapping @ telecom C. Simon, H. de Riedmatten, M. Afzelius, N. Sangouard, H. Zbinden and N. Gisin Phys. Rev. Lett. 98, 190503 (2007) 54
Requirements for Quantum Repeaters GAP Optique 1. Distribution of entanglement over long distances 2. Multi-mode quantum memories 3. Entanglement swapping @ telecom C. Simon, H. de Riedmatten, M. Afzelius, N. Sangouard, H. Zbinden and N. Gisin Phys. Rev. Lett. 98, 190503 (2007) 54
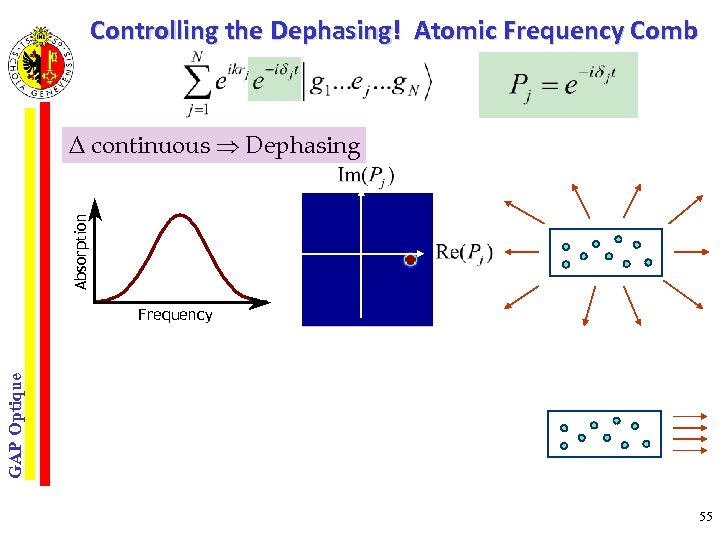 Controlling the Dephasing! Atomic Frequency Comb Absorption Δ continuous Dephasing Frequency Absorption GAP Optique Δ periodic Rephasing Frequency Rephasing after 55
Controlling the Dephasing! Atomic Frequency Comb Absorption Δ continuous Dephasing Frequency Absorption GAP Optique Δ periodic Rephasing Frequency Rephasing after 55
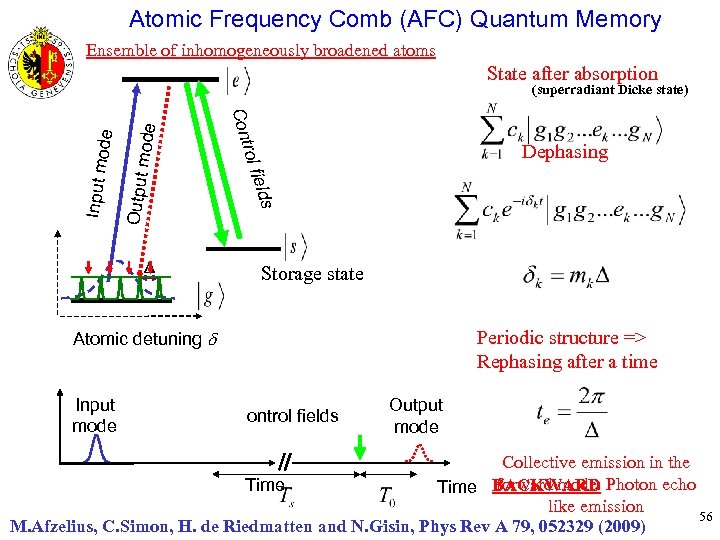 Atomic Frequency Comb (AFC) Quantum Memory Ensemble of inhomogeneously broadened atoms State after absorption mode Output ields Input m Dephasing trol f Atomic density Con ode (superradiant Dicke state) D Storage state GAP Optique Intensity Atomic detuning Input mode Output Control fields mode Periodic structure => Rephasing after a time Output mode Collective emission in the forward mode. Time BACKWARD Photon echo like emission 56 M. Afzelius, C. Simon, H. de Riedmatten and N. Gisin, Phys Rev A 79, 052329 (2009)
Atomic Frequency Comb (AFC) Quantum Memory Ensemble of inhomogeneously broadened atoms State after absorption mode Output ields Input m Dephasing trol f Atomic density Con ode (superradiant Dicke state) D Storage state GAP Optique Intensity Atomic detuning Input mode Output Control fields mode Periodic structure => Rephasing after a time Output mode Collective emission in the forward mode. Time BACKWARD Photon echo like emission 56 M. Afzelius, C. Simon, H. de Riedmatten and N. Gisin, Phys Rev A 79, 052329 (2009)
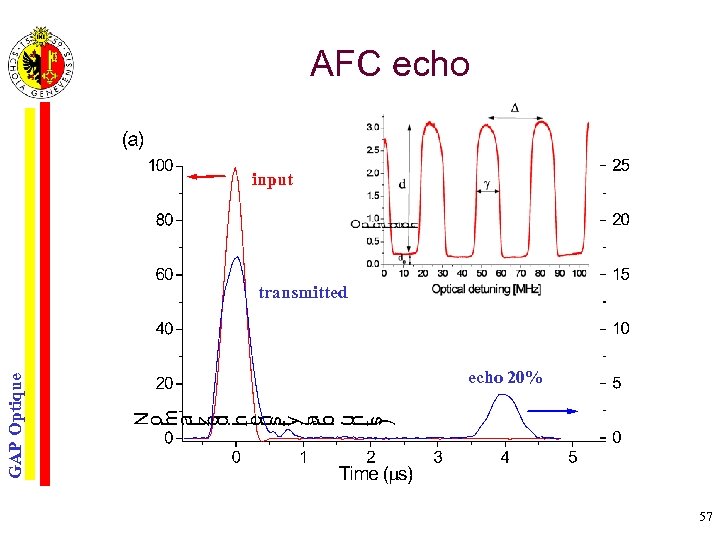 AFC echo input GAP Optique transmitted echo 20% 57
AFC echo input GAP Optique transmitted echo 20% 57
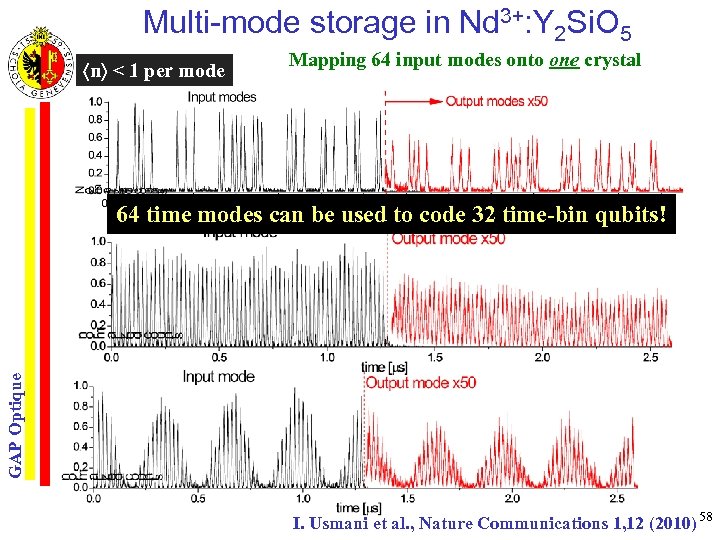 Multi-mode storage in Nd 3+: Y 2 Si. O 5 n < 1 per mode Mapping 64 input modes onto one crystal GAP Optique 64 time modes can be used to code 32 time-bin qubits! I. Usmani et al. , Nature Communications 1, 12 (2010) 58
Multi-mode storage in Nd 3+: Y 2 Si. O 5 n < 1 per mode Mapping 64 input modes onto one crystal GAP Optique 64 time modes can be used to code 32 time-bin qubits! I. Usmani et al. , Nature Communications 1, 12 (2010) 58
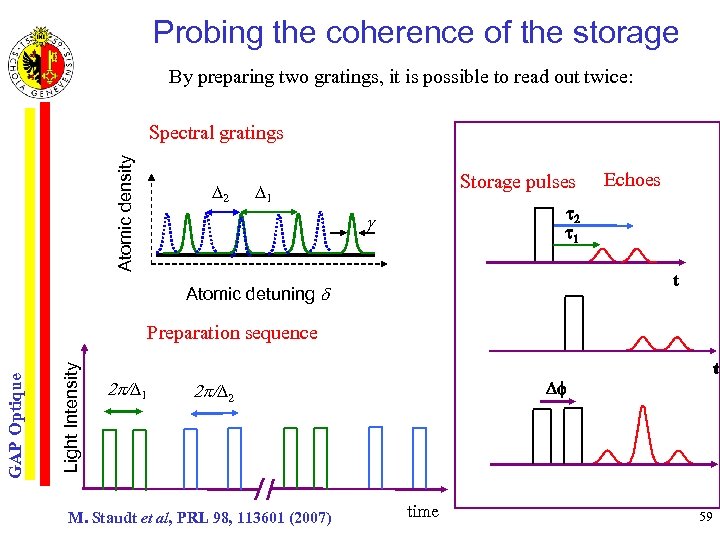 Probing the coherence of the storage By preparing two gratings, it is possible to read out twice: Atomic density Spectral gratings D 2 Storage pulses D 1 Echoes t 2 t 1 g Atomic detuning Light Intensity GAP Optique Preparation sequence 2 p/D 1 Df 2 p/D 2 M. Staudt et al, PRL 98, 113601 (2007) time 59
Probing the coherence of the storage By preparing two gratings, it is possible to read out twice: Atomic density Spectral gratings D 2 Storage pulses D 1 Echoes t 2 t 1 g Atomic detuning Light Intensity GAP Optique Preparation sequence 2 p/D 1 Df 2 p/D 2 M. Staudt et al, PRL 98, 113601 (2007) time 59
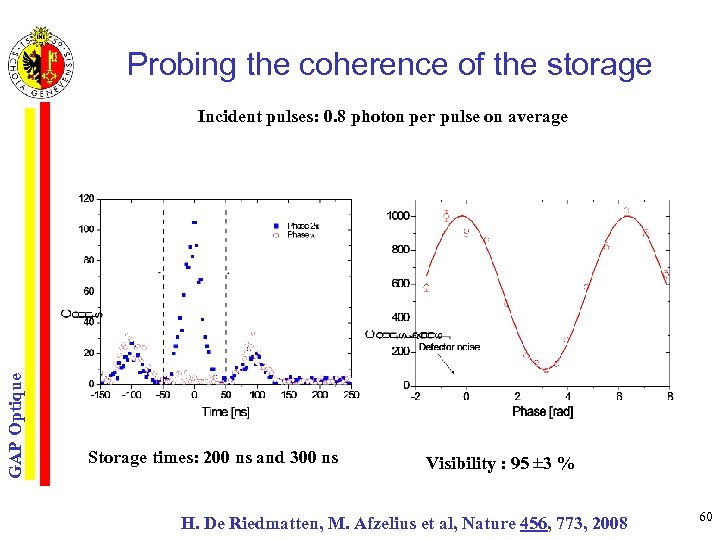 Probing the coherence of the storage GAP Optique Incident pulses: 0. 8 photon per pulse on average Storage times: 200 ns and 300 ns Visibility : 95 ± 3 % H. De Riedmatten, M. Afzelius et al, Nature 456, 773, 2008 60
Probing the coherence of the storage GAP Optique Incident pulses: 0. 8 photon per pulse on average Storage times: 200 ns and 300 ns Visibility : 95 ± 3 % H. De Riedmatten, M. Afzelius et al, Nature 456, 773, 2008 60
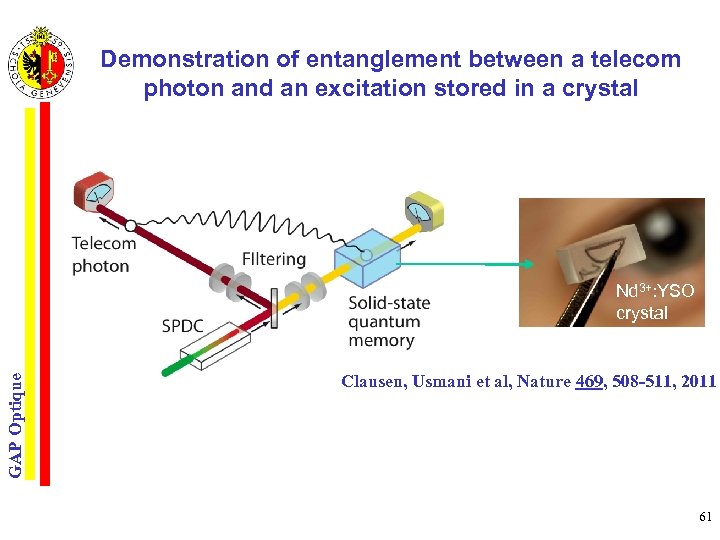 Demonstration of entanglement between a telecom photon and an excitation stored in a crystal GAP Optique Nd 3+: YSO crystal Clausen, Usmani et al, Nature 469, 508 -511, 2011 61
Demonstration of entanglement between a telecom photon and an excitation stored in a crystal GAP Optique Nd 3+: YSO crystal Clausen, Usmani et al, Nature 469, 508 -511, 2011 61
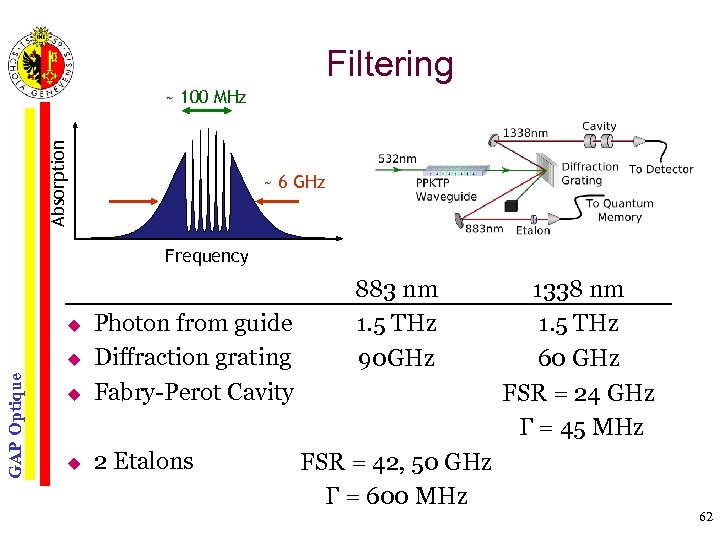 Filtering Absorption ~ 100 MHz ~ 6 GHz Frequency Photon from guide Diffraction grating Fabry-Perot Cavity 2 Etalons GAP Optique 883 nm 1. 5 THz 90 GHz FSR = 42, 50 GHz Γ = 600 MHz 1338 nm 1. 5 THz 60 GHz FSR = 24 GHz Γ = 45 MHz 62
Filtering Absorption ~ 100 MHz ~ 6 GHz Frequency Photon from guide Diffraction grating Fabry-Perot Cavity 2 Etalons GAP Optique 883 nm 1. 5 THz 90 GHz FSR = 42, 50 GHz Γ = 600 MHz 1338 nm 1. 5 THz 60 GHz FSR = 24 GHz Γ = 45 MHz 62
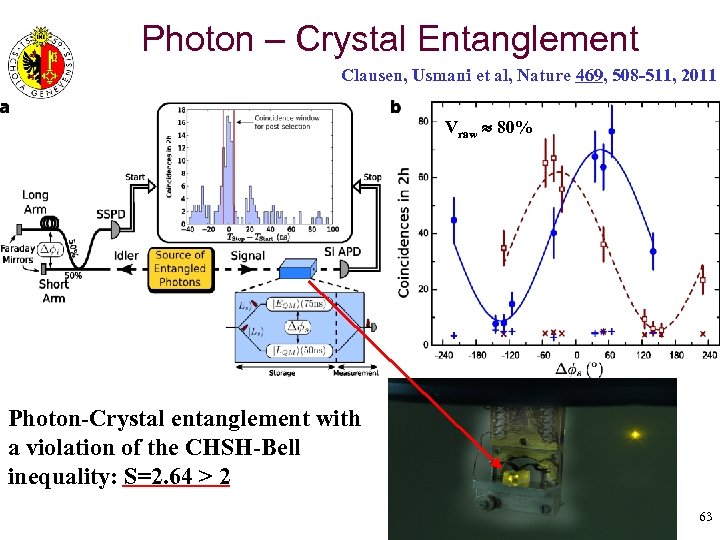 Photon – Crystal Entanglement Clausen, Usmani et al, Nature 469, 508 -511, 2011 GAP Optique Vraw 80% Photon-Crystal entanglement with a violation of the CHSH-Bell inequality: S=2. 64 > 2 63
Photon – Crystal Entanglement Clausen, Usmani et al, Nature 469, 508 -511, 2011 GAP Optique Vraw 80% Photon-Crystal entanglement with a violation of the CHSH-Bell inequality: S=2. 64 > 2 63
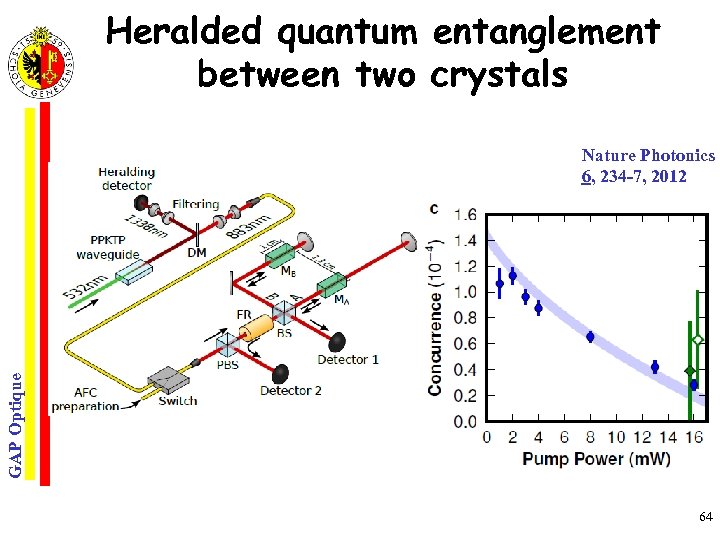 Heralded quantum entanglement between two crystals GAP Optique Nature Photonics 6, 234 -7, 2012 64
Heralded quantum entanglement between two crystals GAP Optique Nature Photonics 6, 234 -7, 2012 64
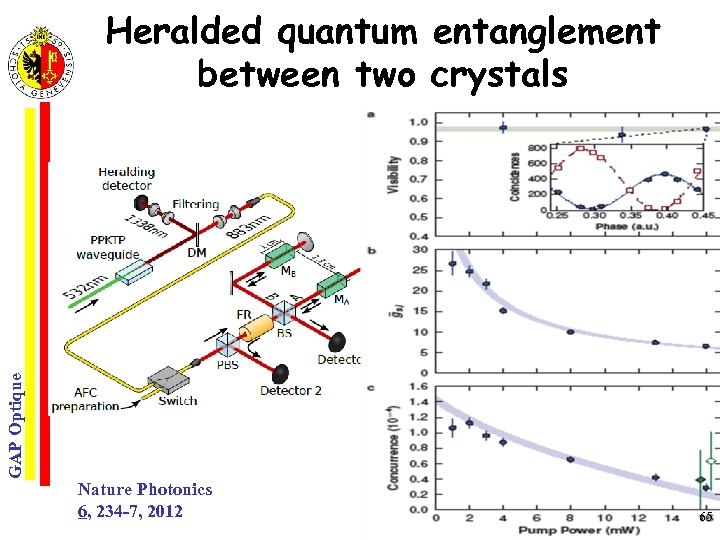 GAP Optique Heralded quantum entanglement between two crystals Nature Photonics 6, 234 -7, 2012 65
GAP Optique Heralded quantum entanglement between two crystals Nature Photonics 6, 234 -7, 2012 65
 Bit rate of the 1 st transatlantic telegram GAP Optique How long did it take to transmit this congratulation in 1858 ? "The Queen desires to congratulate the President upon the successful completion of this great international work, in which the Queen has taken the deepest interest. The Queen is convinced that the President will join with her in fervently hoping that the electric cable, which now connects Great Britain with the United States, will prove an additional link between the two places whose friendship is founded upon their common interests and reciprocal esteem. The Queen has much pleasure in thus directly communicating with the President, and in renewing to him her best wishes for the prosperity of the United States. " 17 hours ! (1 letter took 2 minutes) http: //www. itelegram. com/telegram/Atlantic_Cable_150. asp http: //epe. lac-bac. gc. ca/100/205/301/ic/cdc/cable/fmessages. htm 66
Bit rate of the 1 st transatlantic telegram GAP Optique How long did it take to transmit this congratulation in 1858 ? "The Queen desires to congratulate the President upon the successful completion of this great international work, in which the Queen has taken the deepest interest. The Queen is convinced that the President will join with her in fervently hoping that the electric cable, which now connects Great Britain with the United States, will prove an additional link between the two places whose friendship is founded upon their common interests and reciprocal esteem. The Queen has much pleasure in thus directly communicating with the President, and in renewing to him her best wishes for the prosperity of the United States. " 17 hours ! (1 letter took 2 minutes) http: //www. itelegram. com/telegram/Atlantic_Cable_150. asp http: //epe. lac-bac. gc. ca/100/205/301/ic/cdc/cable/fmessages. htm 66
 Conclusions q Quantum cryptography is a beautiful idea ! (RMP 74, 145195, 2002) q q GAP Optique q q Quantum cryptography exists: you can buy it ! Quantum cryptography relates basic physics to the telecom industry: – from quantum correlations to optical fibers, – from Bell inequalities to security, – from optimal cloning to Shannon information, etc. = the possibility to teleport the "ultimate Q teleportation with: structure" of an object from one place to (Nature 421, 509, 2003) another, without the object ever being Q memories for quantum repeaters anywhere in between 67
Conclusions q Quantum cryptography is a beautiful idea ! (RMP 74, 145195, 2002) q q GAP Optique q q Quantum cryptography exists: you can buy it ! Quantum cryptography relates basic physics to the telecom industry: – from quantum correlations to optical fibers, – from Bell inequalities to security, – from optimal cloning to Shannon information, etc. = the possibility to teleport the "ultimate Q teleportation with: structure" of an object from one place to (Nature 421, 509, 2003) another, without the object ever being Q memories for quantum repeaters anywhere in between 67


