3bc03b73e0dd1fbc1b3a751bf378112f.ppt
- Количество слайдов: 15

Quantum Certificate Complexity Scott Aaronson UC Berkeley
![0 -1 -NPC - #L/poly - #P - #W[t] - +EXP - +L/poly - 0 -1 -NPC - #L/poly - #P - #W[t] - +EXP - +L/poly -](https://present5.com/presentation/3bc03b73e0dd1fbc1b3a751bf378112f/image-2.jpg)
0 -1 -NPC - #L/poly - #P - #W[t] - +EXP - +L/poly - +P - +SAC 1 - A 0 PP - AC 0[m] - ACC 0 - AH - AL – Alg. P/poly - AM intersect co. AM - Amp. MP - APP - APX - AVBPP - Av. E - Av. P AW[P] - AWPP - AW[SAT] - AW[*] - AW[t] - βP - BH - BPEE - BPHSPACE(f(n)) - BPL - BPPKT - BPPOBDD - BPPpath - BPQP - BPSPACE(f(n)) - BPTIME(f(n)) - BQNC - BQNP - BQP-OBDD - BQP/log - BQP/qlog BQTIME(f(n)) - k-BWBP - C=L - C=P - CFL - CLOG - CH - Check - Ck. P - CNP - co. AM - co. C=P - cofr. IP - Coh co. MA - co. Modk. P - comp. IP - comp. NP -co. NE - co. NEXP - co. NL - co. NP/poly - co. RE - co. RNC - co. RP co. UCC - CP - CSIZE(f(n)) - CSL - CZK - D#P - Δ 2 P - δ-BPP - δ-RP - DET - Dis. NP - Dist. NP - DSPACE(f(n)) - DTIME(f(n)) - Dyn-FO - Dyn-Th. C 0 - EESPACE - EEXP - EH - ELEMENTARY - ELk. P - EPTAS k-EQBP - EQTIME(f(n)) - ESPACE - EXP/poly - EXPSPACE - Few. P - FNL/poly - FNP - FO(t(n)) - FOLL – FPNP[log] - FPRAS - FPTnu - FPTsu - FPTAS - FQMA - fr. IP - F-TAPE(f(n)) - FTIME(f(n)) - Gap. L - Gap. P - GC(s(n), C) - GPCD(r(n), q(n)) - G[t] - Hk. P - HVSZK - IC[log, poly] - IP - LIN - Lk. P - LOGCFL - Log. Few. NL - LOGNP - LOGSNP - L/poly - LWPP - MA’ - MAC 0 - MA-EXP - m. AL - Max. NP - Max. PB - Max. SNP 0 - mco. NL - Min. PB - MIPEXP - (Mk)P - m. L - m. NC 1 - m. NL m. NP - Modk. L - Modk. P - Mod. Zk. L - m. P - MPC - m. P/poly - m. TC 0 - NC 1 - NC 2 - NEEXP - NEXP - NIQSZK - NISZKh - NLIN - NLOG - NL/poly - NPC - NPI - NP intersect co. NP - (NP intersect co. NP)/poly - NPMV-sel - NPMVt-sel - NPOPB - NP/poly (NP, P-samplable) - NPR - NPSPACE - NPSV-sel - NPSVt-sel - NQP - NSPACE(f(n)) - NT NTIME(f(n)) - OCQ - Opt. P - P#P[1] - PBP - k-PBP - PCD(r(n), q(n)) - P-close - PCP(r(n), q(n)) - PEXP - PFCHK(t(n)) - Φ 2 P - Ph. P - Π 2 P - PKC - PL 1 - PLinfinity - PLF - PLL - P/log - PNP[k] - PNP[log] - POBDD - PODN - poly. L - PPADS - P/poly - PPP - PQUERY - PR - Pr. HSPACE(f(n)) Promise. BPP - Promise. BQP - Promise. RP - Pr. SPACE(f(n)) - P-Sel - PSK - PT 1 - PTAPE - PTAS PT/WK(f(n), g(n)) - PZK - QAC 0[m] - QACC 0 - QAM - QCFL - QH - QIP(2) - QMA+ - QMA(2) QMAlog - QMAM - QMIPle - QMIPne - QNC 0 - QNCf 0 - QNC 1 - QPSPACE - QSZK - REG Rev. SPACE(f(n)) - RHL - RNC - RPP - RSPACE(f(n)) - S 2 P - SAC 0 - SAC 1 - SBP - SC - SEH - SFk Σ 2 P - SKC - SLICEWISE PSPACE - SNP - SO-E - SP - span-P - SPARSE - SPL - SPP - SUBEXP - sym. P SZK - SZKh - TALLY - TC 0 - Θ 2 P - TREE-REGULAR - UCC - UL/poly - UP - US - VNCk - VNPk - VPk VQPk - W[1] - WAPP - W[P] - WPP - W[SAT] - W[*] - W[t] - W*[t] - XPuniform - YACC - ZPE - ZPP SHAMELESS PLUG /z n so on ar ~a u/ ed y. le e rk. be s ht : // tp . c ww w o. o ml ht

Overview • Most of what’s known about quantum computing can be cast in the query complexity model • Despite its simplicity, open problems abound • We make progress on some of these by studying randomized certificate complexity RC(f) and quantum certificate complexity QC(f) • Main results I’ll discuss today: • We’ll need both big quantum lower bound methods (adversary method and polynomial method)

Background f: {0, 1}n {0, 1} is a total Boolean function D(f) (deterministic query complexity) R 0(f) (zero-error randomized) R 2(f) (bounded-error randomized) Q 2(f) (bounded-error quantum) Q 0(f) (zero-error quantum) QE(f) (exact quantum)

Example

Certificate Complexity CX(f) = min # of queries needed to distinguish X from every Y s. t. f(Y) f(X) Block Sensitivity bs. X(f) = max # of disjoint blocks B {x 1, …, xn} s. t. flipping B changes f(X) Example: For f=MAJ(x 1, x 2, x 3, x 4, x 5), letting X=11110, 11110 CX(MAJ)=3 bs. X(MAJ)=2

Randomized Certificate Complexity RCX(f) = min # of randomized queries needed to distinguish X from any Y s. t. f(Y) f(X) with ½ prob. Quantum Certificate Complexity QC(f) Example: For f=MAJ(x 1, …, xn), letting X=00… 0, RCX(MAJ) = 1 Observations: Anything a prover might provide a verifier besides X, the verifier can compute for itself One-sided and two-sided error are equivalent Different notions of nondeterministic quantum query complexity: Watrous 2000, de Wolf 2002

Ambainis’ Adversary Method (special case) Let D 0, D 1 be distributions over f-1(0), f-1(1) s. t. D 0 looks “locally similar” to every 1 -input, and D 1 looks “locally similar” to every 0 -input: Then

Claim: • Any randomized certificate for input X can be made nonadaptive with constant blowup • By minimax theorem, exists distribution over {Y: f(Y) f(X)} s. t. for all i, xi yi w. p. O(1/RC(f)) • Adversary method then yields • For upper bound, use “weighted Grover”
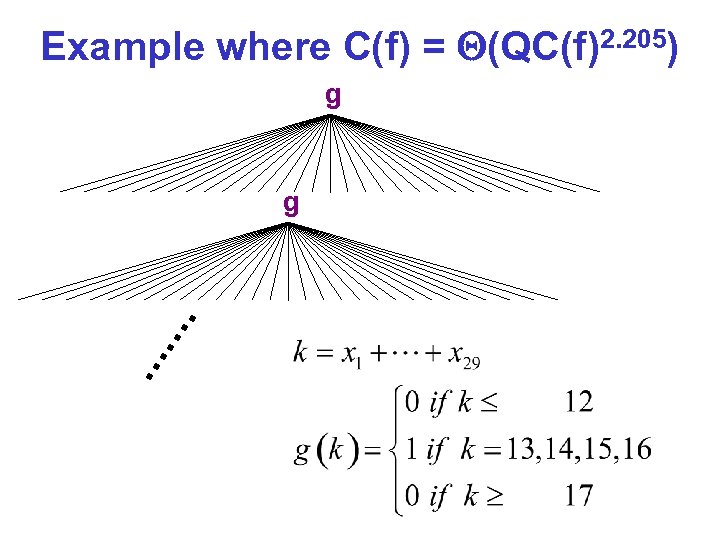
Example where C(f) = (QC(f)2. 205) g g

New Quantum/Classical Relation For total f, where ndeg(f) = min degree of poly p s. t. p(X) 0 f(X)=1 Previous: D(f) = O(Q 2(f)2 Q 0(f)2) (de Wolf), D(f) = O(Q 2(f)6) (Beals et al. )

Idea (follows Buhrman-de Wolf): Let p be s. t. p(X) 0 f(X)=1 Maxonomials of p are monomials not dominated by other monomials—i. e. maxonomials of x 1 x 2 – x 2 + 2 x 3 are x 1 x 2, 2 x 3 Nisan-Smolensky: For every 0 -input X and maxonomial M of p, X has a sensitive block whose variables are all in M Consequence: Randomized 0 -certificate must intersect each maxonomial w. p. ½ Randomized algorithm: Keep querying a randomized 0 -certificate, until either one no longer exists or p=0

Lemma: O(ndeg(f) log n) iterations suffice w. h. p. Proof: Let S be current set of monomials, and Initially (S) nndeg(f)! We’re done when (S)=0 Claim: Each iteration decreases (S) by expected amount (S)/4 e Reason: 1/e of (S) is concentrated on maxonomials, each of which decreases in degree w. p. ½

Local Proofs • When faced with a hard problem, analyze limitations of known techniques (Baker-Gill. Solovay, Razborov-Rudich) • Is • I claim that a ‘yes’ answer would require “global analysis” of Boolean functions • Given n n lattice of bits X, let f(X)=1 if there’s a square ‘frame’ of size n 1/3, f(X)=0 otherwise

Open Problems • Is ~ • Is If so we get
3bc03b73e0dd1fbc1b3a751bf378112f.ppt