QUANTITATIVE THEORY OF THERMAL FLUCTUATIONS AND DISORDER IN

QUANTITATIVE THEORY OF THERMAL FLUCTUATIONS AND DISORDER IN THE VORTEX MATTER Dingping Li School of Physics, Peking University, China Baruch Rosenstein, NCTS&NCTU, Hsinchu, Taiwan, Weizmann Institute&Bar Ilan, Israel IVW 2005, TIFR, India Jan. 11(2005) 1

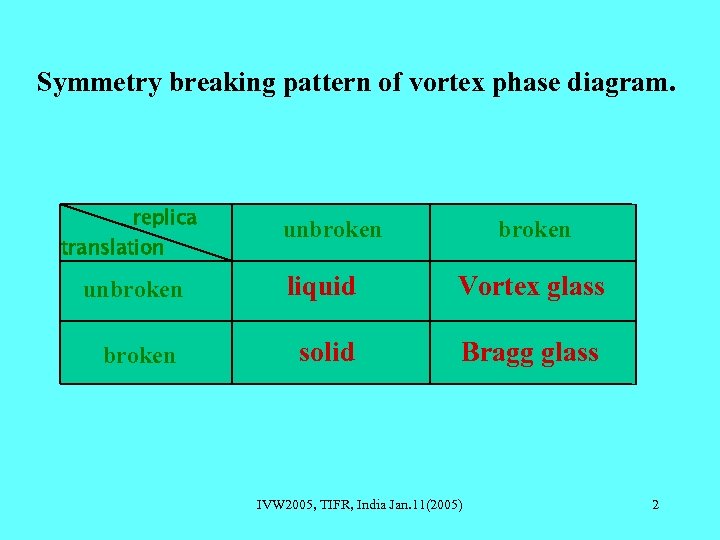Symmetry breaking pattern of vortex phase diagram. replica translation unbroken liquid Vortex glass broken solid Bragg glass IVW 2005, TIFR, India Jan. 11(2005) 2

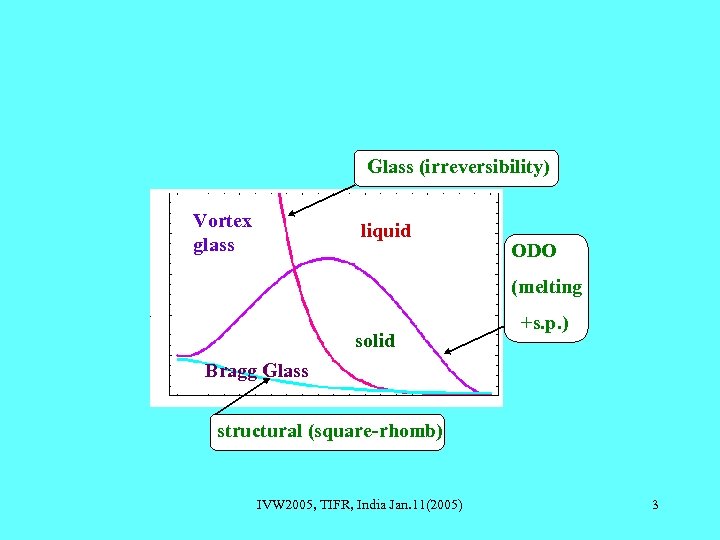Glass (irreversibility) Vortex glass liquid ODO (melting solid +s. p. ) Bragg Glass structural (square-rhomb) IVW 2005, TIFR, India Jan. 11(2005) 3

Ginzburg – Landau theory and the LLL approximation Thermal fluctuations are taken into account using the statistical sum with the GL energy in 2 D (for simplicity) with variances IVW 2005, TIFR, India Jan. 11(2005) 4

Within the LLL approximation the gradient term is combined with the quadratic. Therefore without disorder physical quantities depend on a single parameter: Rugger Thouless, 1975 i, IVW 2005, TIFR, India Jan. 11(2005) 5

Thermal fluctuations Vortex Solid: 1. For the free energy we get to the required precision (. 1%) at the two loop order (the IR divergencies due to “supersoft” phonons cancel exactly) : 2. Using gaussian approximation one finds that the solid becomes unstable at (spinodal). BR PRB 60, 4268 (1999) DPL, BR PRB 65, 024514(2001) Spinodal Vortex liquid 1. We constructed the Optimized gaussian series, which are convergent rather than asymptotic. Radius of convergence is IVW 2005, TIFR, India Jan. 11(2005) 6

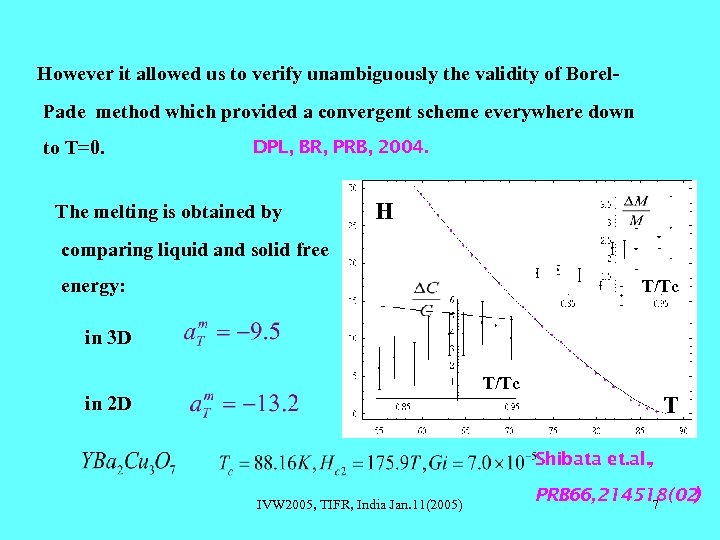However it allowed us to verify unambiguously the validity of Borel. Pade method which provided a convergent scheme everywhere down to T=0. DPL, BR, PRB, 2004. The melting is obtained by H comparing liquid and solid free energy: T/Tc in 3 D T/Tc in 2 D T Shibata et. al. , IVW 2005, TIFR, India Jan. 11(2005) PRB 66, 214518(02 ) 7

Point disorder, Unified ODO line, Kauzmann points 1. Disorder breaks the LLL scaling. Using perturbation around the zero disorder overcooled liquid and solid, we find that there is a single order – disorder line combining the melting line and the second peak line. Liquid gains more than solid from pinning and the line “curves down” at Kauzmann point in which the entropy jump vanishes. 2. The continuation of the “clean” melting line becomes a crossover (Hx) between liquid I and a viscous liquid II which we characterize as strongly correlated (deeply supercooled). Tricritical point is reinterpreted as a Kauzmann point. 3. In 3 D the line has a “wiggle”. IVW 2005, TIFR, India Jan. 11(2005) 8

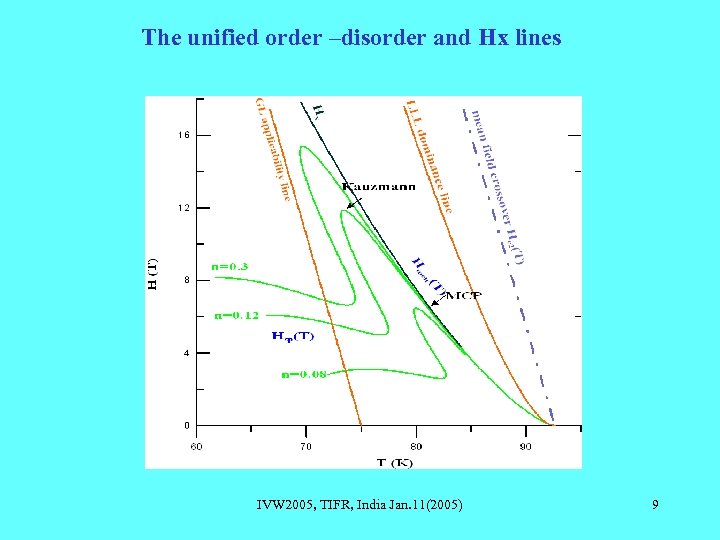The unified order –disorder and Hx lines IVW 2005, TIFR, India Jan. 11(2005) 9

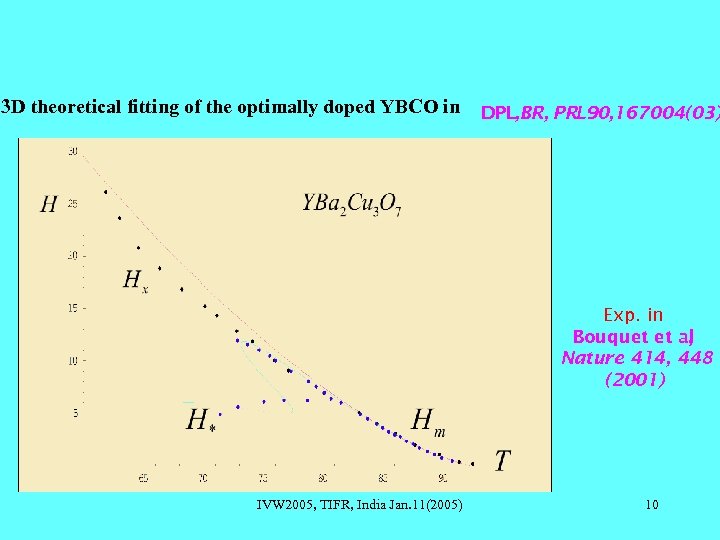3 D theoretical fitting of the optimally doped YBCO in DPL, BR, PRL 90, 167004(03) Exp. in Bouquet et al , Nature 414, 448 (2001) IVW 2005, TIFR, India Jan. 11(2005) 10

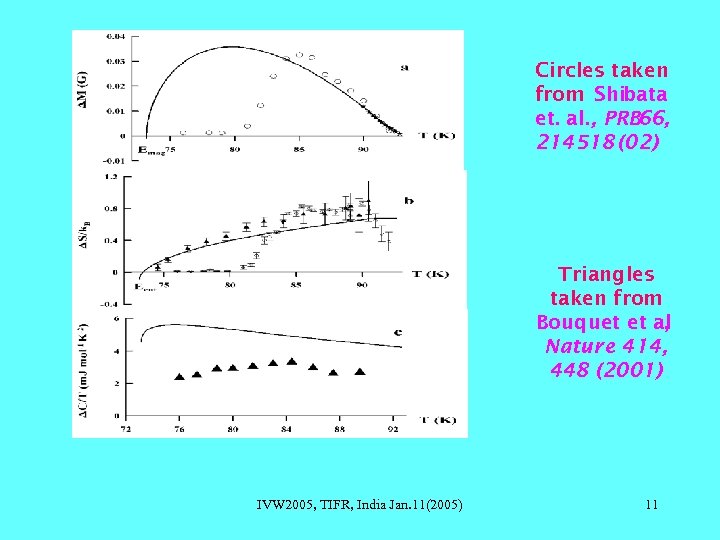Circles taken from Shibata et. al. , PRB 66, 214518 (02) Triangles taken from Bouquet et al , Nature 414, 448 (2001) IVW 2005, TIFR, India Jan. 11(2005) 11

Replica symmetry breaking-Glass transition To calculate disorder averages we can use replica trick to integrate over disorder. Then we use the Mezard –Parisi Gaussian variational method to study the RSB. Lopatin Europhys Let. 51, 635 (00). DPL, BR, cond-mat (04), unpublished. Replica symmetry breaking solution means there is a hierarchy of relaxation times in dynamics (reflecting the logarithmically diverging energy barriers). IVW 2005, TIFR, India Jan. 11(2005) 12

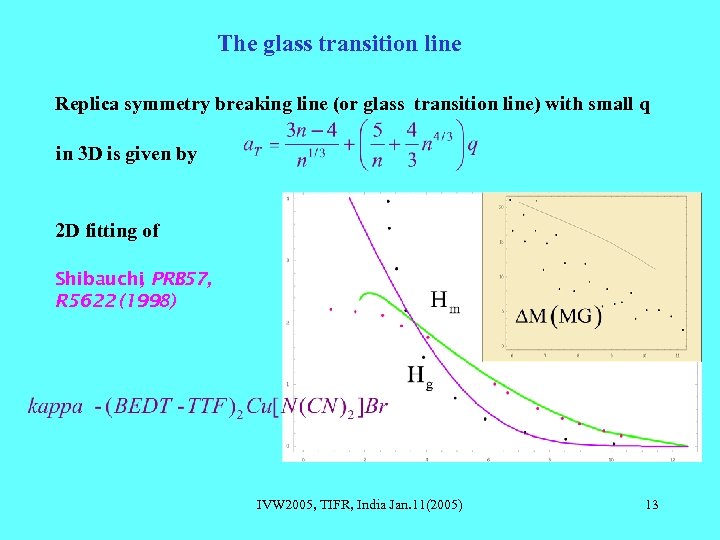The glass transition line Replica symmetry breaking line (or glass transition line) with small q in 3 D is given by 2 D fitting of Shibauchi PRB 57, , R 5622 (1998) IVW 2005, TIFR, India Jan. 11(2005) 13

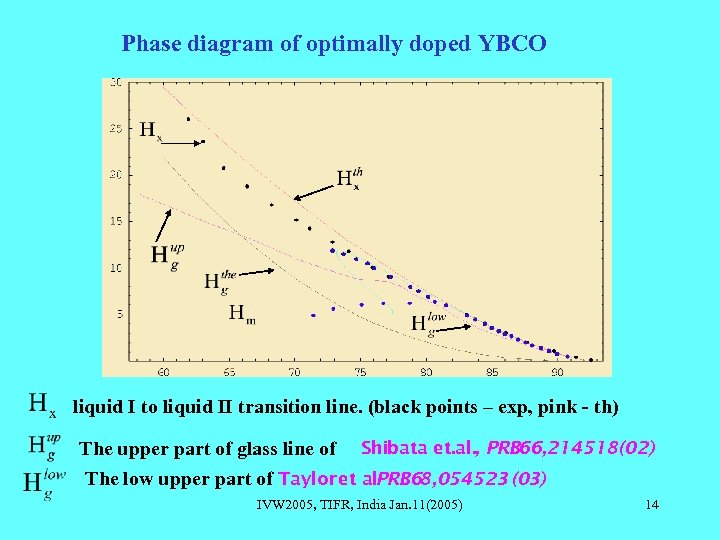Phase diagram of optimally doped YBCO liquid I to liquid II transition line. (black points – exp, pink - th) The upper part of glass line of Shibata et. al. , PRB 66, 214518(02) The low upper part of Taylor et al. PRB 68, 054523 (03) IVW 2005, TIFR, India Jan. 11(2005) 14

Conclusion The LLL GL theory allows qualitative and quantitative comparison with experiment in a wide variety of type II materials in surprisingly wide range of fields and temperatures. It include the melting and the glass lines, in some cases magnetization and specific heat jumps and other quantities. The generic phase diagram contains four phases: liquid, solid, vortex glass and Bragg glass experimentally and Divakaret al, theoretically in our approach. PRL 92, 237004 (04) La. SCO IVW 2005, TIFR, India Jan. 11(2005) 15

Open question: glass line in solid BSCCO Fuchs et al PRL 80, 4911 (2002 ) La. SCO Sasagawaet al PRB 61, 1610 (00) IVW 2005, TIFR, India Jan. 11(2005) YBCO Taylor et al PRB 68, 054523 (03) 16

See our posters for details in Theory (P 56) and Experimental Fitting (P 35) IVW 2005, TIFR, India Jan. 11(2005) 17