Quantitative Research at J P Morgan Who

Quantitative Research at J. P. Morgan

Who we are QR is an expert quantitative modeling group partnering with traders, marketers, and risk managers across all products and regions. • • Currently 260 quants: 170 working on trading desks and 90 working with risk managers Represented in New York, London, Houston, Singapore, Hong Kong, Tokyo, and Sao Paulo

What we do Support of JPM trading businesses § Develop mathematical models for pricing, hedging and risk measurement of derivatives § Develop algorithms for electronic trading and order execution § Explain model behavior, identify sources of risk in portfolios, perform scenario analysis § Develop and deliver analytics in software and systems § Develop tools for pricing and structuring § Develop models and analytics for counterparty exposure and capital usage Support of Central Risk Management and Finance, both IB and corporate § Risk methodologies and engines § Capital and profitability measurement § Regulatory relations on capital models and model risk Understand control model risk across all of the above § Evaluate quantitative methodologies: identify and monitor model risk associated with valuation and risk models § Assess the appropriateness of quantitative models and their limitations for valuation and risk management In support of all of the above, designing and developing § Software frameworks for analytics § Efficient numerical algorithms and implementing high performance computing

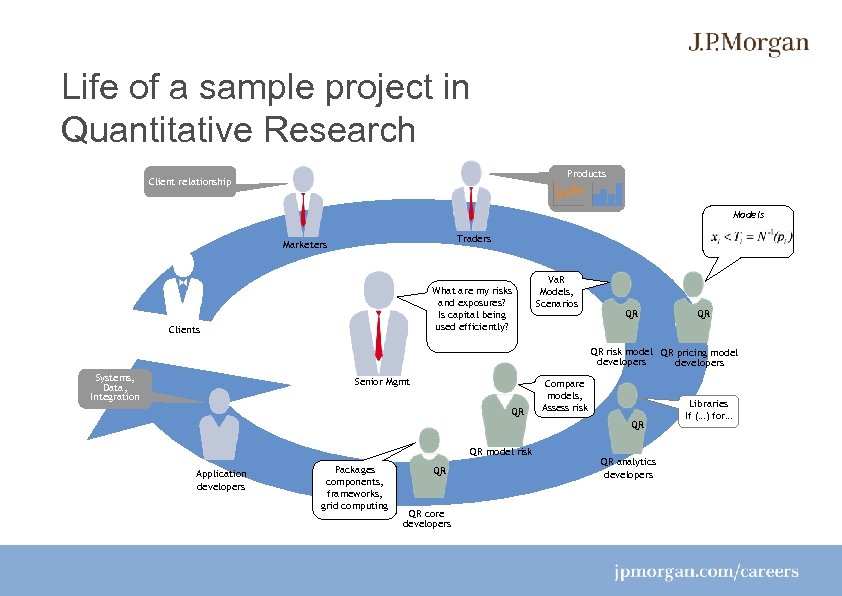Life of a sample project in Quantitative Research Products Client relationship Models Traders Marketers What are my risks and exposures? Is capital being used efficiently? Clients Va. R Models, Scenarios QR QR QR risk model QR pricing model developers Systems, Data, Integration Senior Mgmt QR Compare models, Assess risk QR QR model risk Application developers Packages components, frameworks, grid computing QR QR core developers QR analytics developers Libraries If (…) for…

Example Project in QR: FX Knockout Options Knockout call option: buyer has the right to buy 100 M USD for 1 B JPY in 1 m, but only if the USD/JPY exchange rate doesn’t trade down through 82 before expiration Corporations trade these as a way of marrying efficient hedges for their foreign exchange risk with views on the market An example of a “structured” or “exotic” derivative: one which is tailored for a particular customer, and where there is no liquid market § Need a pricing model to figure out fair value for the knockout option relative to the more liquid markets we use as hedges § The pricing model also lets us perform “dynamic hedging” to manage the risk

Example Project in QR: FX Knockout Options Work with traders and sales force to determine revenue potential of the product § Lots of other projects competing with this for priority! Work with traders to zero in on market dynamics and pricing/risk considerations that are important for the product § In USD/JPY FX, Black-Scholes is not a good enough model because of stochastic volatility § Knockout options are sensitive to stochastic volatility and so we need a stochastic volatility model

Example Project in QR: FX Knockout Options Simple model approach: the Heston model for stochastic volatility

Example Project in QR: FX Knockout Options Solve the resulting PDE for the knockout option price P § Boundary conditions: price = zero for all time at the knockout boundary, price = call option payoff at expiry time § Backward-induct: so start at the expiry time and integrate back through time to today Need full implementation to get it in the hands of traders § § § Numerical implementation of PDE solver Representation of derivative contract in the trading system that calls the PDE pricing Comprehensive testing of implementation for pricing and risk management Review of the model by the Model Review Group Add the new product to pricing and trading tools so traders can make prices and trade

Example Project in QR: Risk Modeling Develop, maintain and support models for estimating counter-party risk on the banks portfolio of OTC derivatives When traders execute a trade with a client they need an estimate of the § fair value of the trade adjusting for the cost of insuring against counter-party default – credit valuation adjustment (CVA): the market price of a credit default swap hedge on the exposure of the trade with the client (counter-party) § expected exposure profile to help calculate CVA and Capital requirements for the trade § peak exposure (worst case loss at a particular confidence level) – Used to decide whether to execute the trade. If risk excessive find a way to mitigate risk. § If other trades with client exist a marginal impact of all the above has to be estimated and portfolio effects have to be taken into account – Netting agreement allows netting of +ve and –ve PV’s – Collateral agreement: Bank or the Client may post collateral – added complexity on top of pure pricing Exposure is the amount we would lose (if they owe us) upon counter-party default.

Example Project in QR: Risk Modeling Bank actively monitors and risk manages its counter-party risk on a daily basis § A CVA reserve (across all counter-parties) is maintained and risk managed by the bank § Risk limits are monitored on each counter-party using a peak exposure measure § To support all this a risk model is run nightly across a large fraction of banks portfolio – Major undertaking that requires central gathering of data and modeling infrastructure and coordination across the business, technology and QR Quants play a central role in working with business and technology, developing, implementing and supporting these models § Support traders and marketers to help provide risk valuation § Work on onboarding new products into risk engine – Implementation of models for market simulation engine if new assets needed – Implement pricer for new products or leverage FO models where possible – Work with technology to onboard model into risk measurement systems § Improve performance by – enhancing pricing algorithms or applying Monte-Carlo variance reduction techniques – applying parallel computing, GPU or other technology tricks

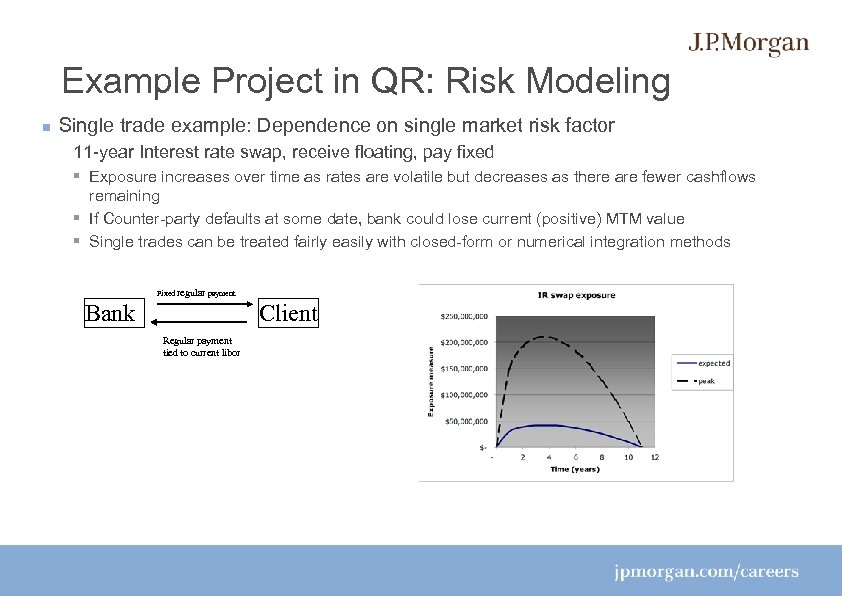Example Project in QR: Risk Modeling Single trade example: Dependence on single market risk factor 11 -year Interest rate swap, receive floating, pay fixed § Exposure increases over time as rates are volatile but decreases as there are fewer cashflows remaining § If Counter-party defaults at some date, bank could lose current (positive) MTM value § Single trades can be treated fairly easily with closed-form or numerical integration methods Fixed regular payment Bank Client Regular payment tied to current libor

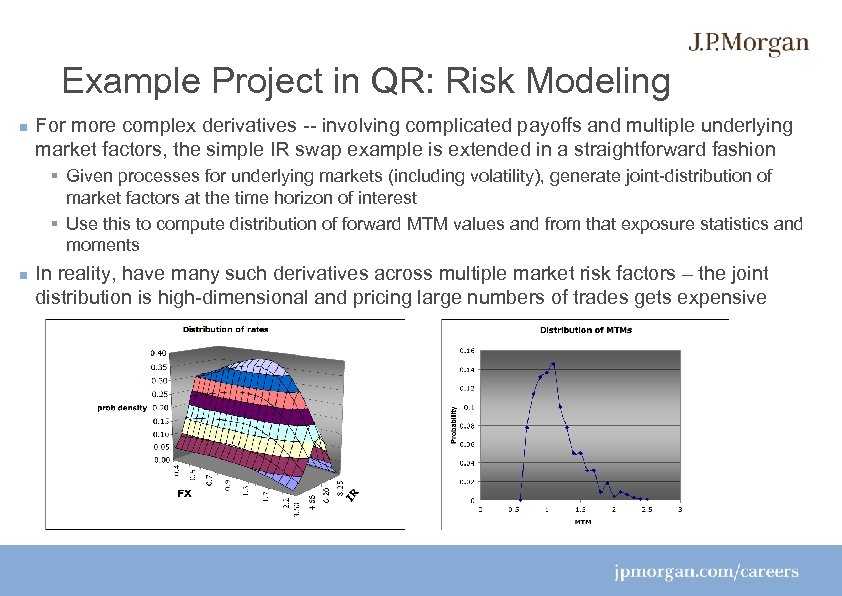Example Project in QR: Risk Modeling For more complex derivatives -- involving complicated payoffs and multiple underlying market factors, the simple IR swap example is extended in a straightforward fashion § Given processes for underlying markets (including volatility), generate joint-distribution of market factors at the time horizon of interest § Use this to compute distribution of forward MTM values and from that exposure statistics and moments In reality, have many such derivatives across multiple market risk factors – the joint distribution is high-dimensional and pricing large numbers of trades gets expensive

Example Project in QR: Risk Modeling Use Monte-Carlo simulation engine for the full problem § Underlying market risk factors across IR, FX, Commodities, Equity, Credit, Energy » High dimensionality: 1000’s of risk factors § Multi-period Cross asset model to generate joint distribution for all risk factors out to 50 years – Require market model captures correlated market dynamics » (for instance - Might use combination of HJM for rates and credit and lognormal for FX, equity) § Price over a million trades across thousands of counter-parties along each Monte Carlo path – Face the challenge of implementing fast pricers for wide variety of trade types of varying complexity – Billions of pricing per simulation – important to implement most efficient pricing algorithms possible § Final counter-party level risk aggregation requires simulation of collateral and netting – Capture details of netting and collateral agreements – collateral treatment is inherently path-dependent § With optionality in the portfolio, collateral agreements and path-dependent payoffs the effective dimensionality is greatly increased Other additional features/complexities that further enrich the problem § Relatedness, pricing DVA, sensitivities of CVA for risk management, etc Interesting swath of problems to solve for Quants encompassing a wide range of skill-sets

Example Project in QR: LVSV Calibration PDE Approach § Suppose we want to calibrate a generic Local-Stochastic Volatility model (LVSV): § Let’s define the local volatility associated to the model as § It is possible to prove that a pure local volatility model with local vol equal to options of our LVSV model prices the same vanilla Given by the market via Dupire’s formula where § In order to illustrate the methodology, let’s decide that the stochastic volatility component of the model is meanreverting and lognormal: We also define θ(t) so that the expectation of the instantaneous variance is equal to 1

Example Project in QR: LVSV Calibration PDE Approach § We introduce the forward joint transition density p(x, y, T) for the logarithm of the spot price S to reach the level x and the logarithm of the stochastic component of the volatility Y=ln(Z) to reach the level y at time T, starting from S=S(0) and Z=1 at time 0. § This density satisfy the Kolmogorov forward equation: § Furthermore, the conditional expectation we are interested in can be written as a function of p § In order to compute the term σ we need to know Φ, to know Φ we need p, but to have p we need to input σ…

Example Project in QR: LVSV Calibration PDE Approach § So we can solve this system of equations using a forward iterative process § Issue with this methodology: quite slow – At each step we need to solve for all x and y

Example Project in QR: LVSV Calibration Alternative Approach § Let’s go back to the generic LVSV model (not assuming mean-reverting lognormal stochastic volatility) § And consider the pure stochastic volatility model associated to this § Let’s denote by the local volatility associated to this model

Example Project in QR: LVSV Calibration Alternative Approach § It is possible to prove that exists a smooth monotone mapping between S and X, X=H(t, S). Using an explicit representation of this function H, we can obtain this formula: where I’m cheating a bit here: the term Λ(T) is not known, but it must be chosen to minimize an equation which, unfortunately, involves σ(T, S). In reality I still need an iterative process to find my calibrated σ(T, S)… § The equation above can be easily solved as long as we know the local volatility associated to the pure stochastic volatility model we have reduced our original problem to a different and easier problem § This approach can be very fast and accurate § Furthermore, it is very general: we haven’t assumed anything yet on the stoch vol dynamics

Example Project in QR: LVSV Calibration Alternative Approach for Heston Model: Fourier Transform § Let’s now assume that the stochastic part of the model has Heston-like dynamics: § In this particular case we can use the Fourier theory for the calibration § Define the Laplace transform of a random variable X with cdf F(x) by: § The basic theory of the Laplace transform tells us: § Let X be the log spot price. Then the price of a European call option is given by:

Example Project in QR: LVSV Calibration Alternative Approach for Heston Model: Fourier Transform Define a new probability measure Hence, the price of the call can be computed as: Using the previous expression for the cumulative probability, the call’s price is: If the Laplace transform of the log spot is known in closed form, the price of a call option can be evaluated by combining a Fourier inversion and a numerical integration

Example Project in QR: LVSV Calibration Alternative Approach for a generic model: Malliavin Calculus § Let’s go back to a generic SDE for the stochastic volatility part and concentrate on the conditional expectation § Our goal is to rewrite this ratio in a more friendly form using the Malliavin Calculus theory § As a first example, suppose to know the joint law p(x, y) of the couple (F, G). where § So, in this easy case, we found a nice expression for this conditional expectation

Example Project in QR: LVSV Calibration Alternative Approach for a generic model: Malliavin Calculus § In general, if we don’t know the joint law p(x, y), using Malliavin calculus it is possible to find a process u such that where the operator δ is the Skorohod integral. § In particular, it is possible to prove the following: Theorem: Consider the pure SVM model The local volatility associated to the model can be written as where

References § Dupire B. (1994), Pricing with a Smile, Risk, pages 18 -20 § Dupire B. , A unified theory of volatility, Derivative Pricing, The Classic Collection, Peter Carr Risk Publication § Ewald C. O. (2005), Local Volatility in the Heston Model: A Malliavin Calculus Approach, Journal of Applied Mathematics and Stochastic Analysis, 2005. Pages 307 -322 § Fournie’ E, Lasry f. , Lebouchoux J. , Lions J. (2001), Application of Malliavin Calculus in Finance II, Finance and Stochastics, pages 201 -236 § Gatheral J (2006), The Volatility Surface – A Practioner’s Guide, John Wiley & Sons, Inc. § Gil-Pelaez J. (1951), Note on the inversion theorem, Biometrika § Heston S. L. (1993), A closed-form solution for pricing with stochastic volatility with applications to bond and currency options, Review of financial studies, 327 -343 § Labordere P. H. (2009), Calibration of local stochastic volatility models to market smiles, Risk, pages 112 -117 § Labordere P. H. (2008), Analysis, Geometry and Modeling in Finance: Advanced Methods in Option Pricing, Chapman & Hall/CRC, Financial Mathematics Series § Lipton A. (2002), The Vol Smile Problem, Risk, Feb § Ren Y. , Madan D. , Qian M. (2007), Calibrating and pricing with embedded local volatility models, Risk, pag. 138 -143

What we’re looking for Our ideal candidate has… Enrolled in math, sciences, engineering, finance or computer science Exceptional analytical, quantitative and problem-solving skills Mastery of advanced mathematics and numerical analysis arising in financial modeling § Experience with advanced statistical models for empirical estimation of risk models Strong knowledge of options pricing theory or econometric modeling § § Linear algebra, probability theory, stochastic processes, differential equations, numerical analysis Quantitative models for pricing and hedging derivatives Econometric models for algorithmic trading and execution models Strong software design and development skills, particularly in C++ Expertise in grid computing, software frameworks, and software life-cycle Excellent presentation skills, both oral and written

Intern project examples Finite difference schemes for jump diffusions Alternative parametric interpolation of smiles Model for options on dividends Malliavin representation of Greeks BGM Model with normal continuously compounded LIBORs Optimized premiums & loan payments for a life settlement contract Linear Programming for the valuation of natural gas contracts Statistical challenges in market risk capital Local volatility using splines A software framework for flexible scenarios for risk management Python client distributed risk simulation

How to apply…. If you are interested in an internship or a full time position, please visit our careers site: www. jpmorgan. com/careers Details of all available roles within Quantitative Research in the EMEA region can be found under Postgraduate Opportunities