Quantitative Analysis Of Competitive Effects For Antitrust Day

Quantitative Analysis Of Competitive Effects For Antitrust Day 2 Luke Froeb Owen Graduate School of Management Vanderbilt University April 2003

Topics in Merger Simulation The Cruise Lines Merger Issues in Demand Estimation Mergers in Auction Markets Luke Froeb Owen Graduate School of Management Vanderbilt University

The Cruise Lines Merger Luke Froeb Owen Graduate School of Management Vanderbilt University

Cruise Line Merger: Outline Joint work with Steven Tschantz (Math Dept. ) • Revenue management and cruise line merger • Revenue management for economists • Nash equilibrium when firms “revenue manage” • • Usual ownership effect raises price • Information sharing effect can raise or lower price Model extensions • Policy conclusions •

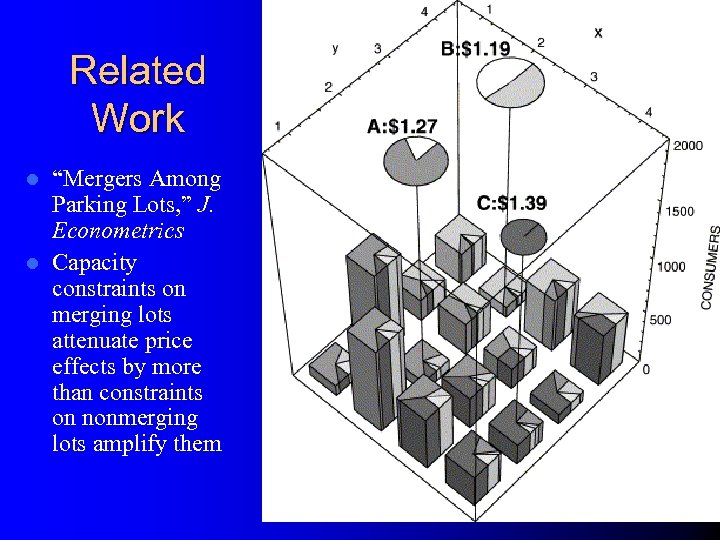Related Work “Mergers Among Parking Lots, ” J. Econometrics l Capacity constraints on merging lots attenuate price effects by more than constraints on nonmerging lots amplify them l

Carnival and Princess Revenue Management • Revenue management: problem of matching uncertain demand to available capacity • Hotels, airlines, cruise lines • UK Competition Commission, U. S. FTC, and EC all cleared cruise line merger • Theories considered by the FTC • Filling the ship concern unaffected by merger so no merger effect • No quantity effect, but higher prices to less elastic customers • Were theories correct? What was magnitude?

Revenue Mgmt. for Economists • Price is set before demand realized • Fixed capacity (big fixed costs, low marginal cost) • Q = min[demand(p), K] • demand[p] is randomly distributed around mean q[p] • q[p] is a logit function of price • If C(Q) is linear, • E[π(p)] = E[p Q(p) – C(Q(p))] = p E[Q(p)] – C(E[Q(p)]) • Expected profit is a function of expected quantity • Uncertainty can cause price to be higher or lower than the deterministic price depending on the “costs” of over vs. under pricing

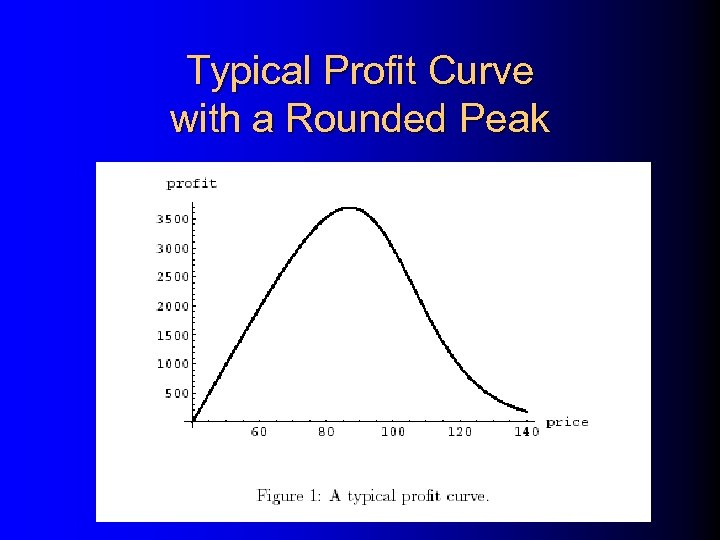Typical Profit Curve with a Rounded Peak

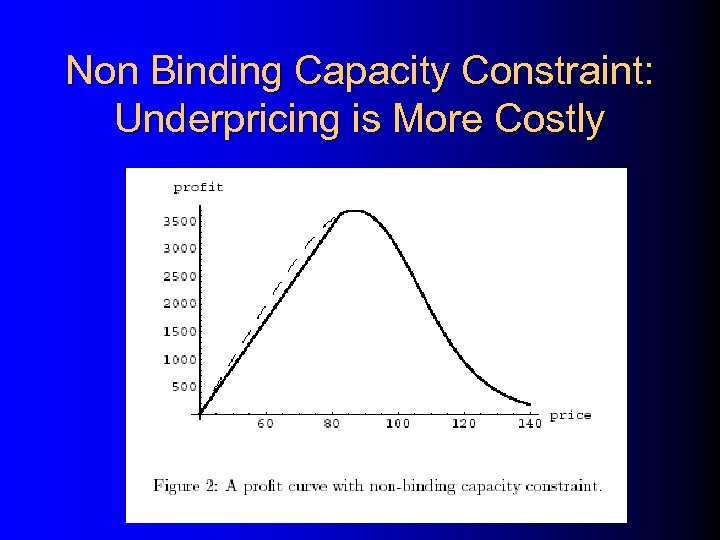Non Binding Capacity Constraint: Underpricing is More Costly

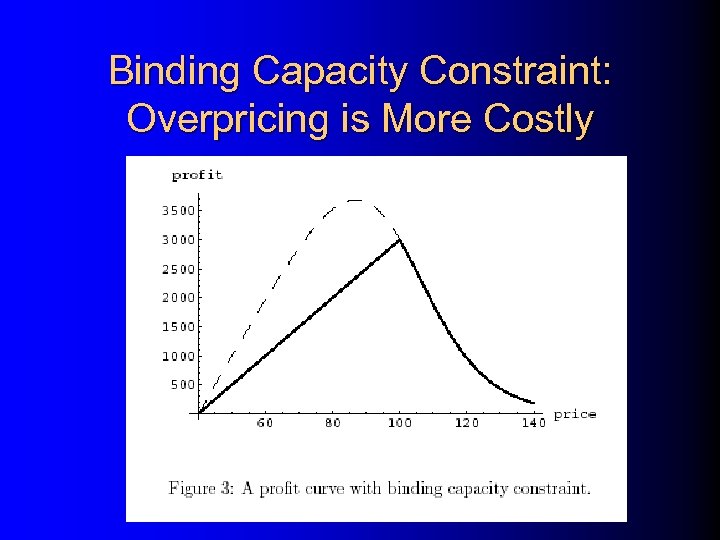Binding Capacity Constraint: Overpricing is More Costly

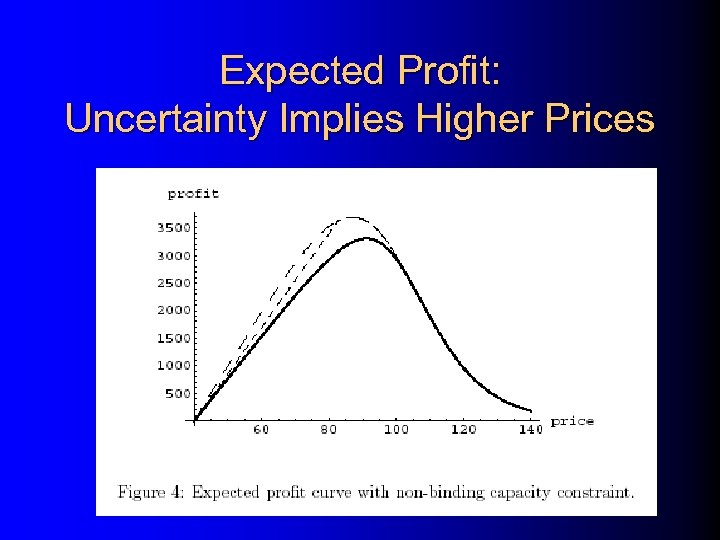Expected Profit: Uncertainty Implies Higher Prices

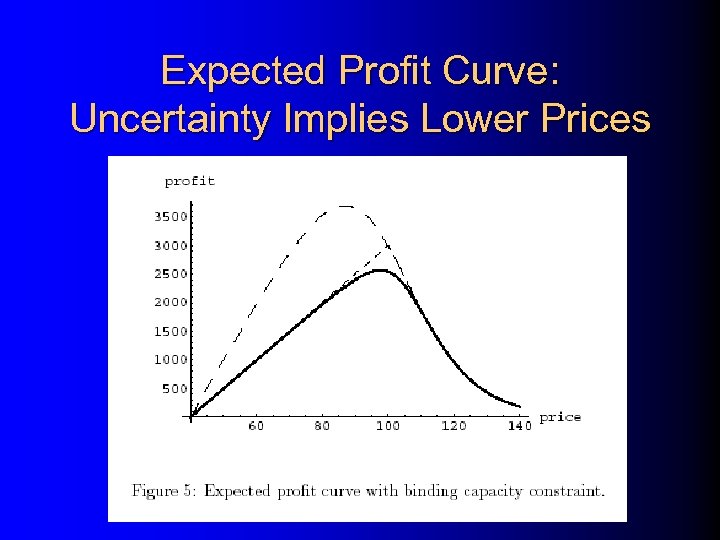Expected Profit Curve: Uncertainty Implies Lower Prices

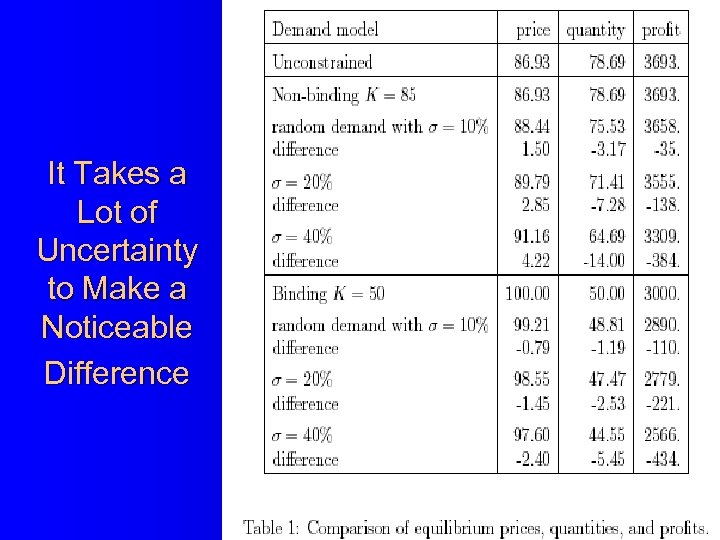It Takes a Lot of Uncertainty to Make a Noticeable Difference

Poisson Arrival Process on Top of Logit Choice Model Poisson arrival process with mean µ l On top of n choice logit demand model l Implies n independent arrival processes with means (siµ) l

Role of Information Gamma(α, β) prior on unknown mean arrivals; conjugate to Poisson l Each firmi observes fraction βi (common knowledge), and gets a private signal αi successes l Firm’s posterior information characterized by Gamma(α + αi, β + βi) on unknown µ l

Nash Equilibrium • Optimal price maximizes expected profit as a function of own signal, pi(αi) • Expectation over all possible signals and all possible quantities

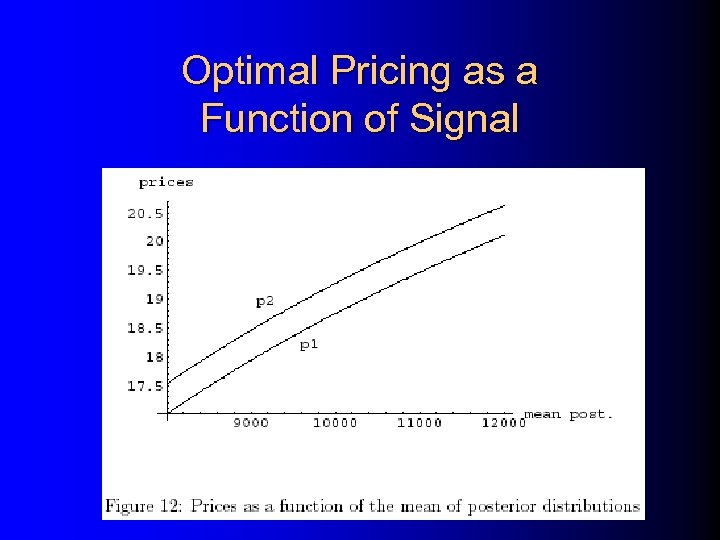Optimal Pricing as a Function of Signal

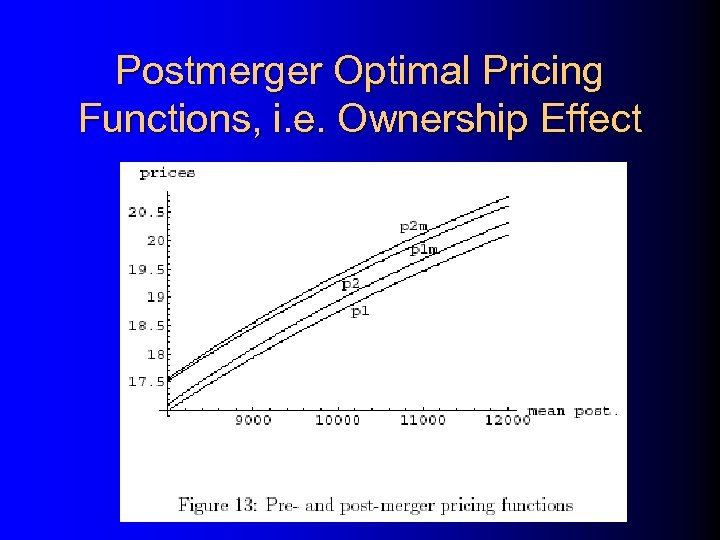Postmerger Optimal Pricing Functions, i. e. Ownership Effect

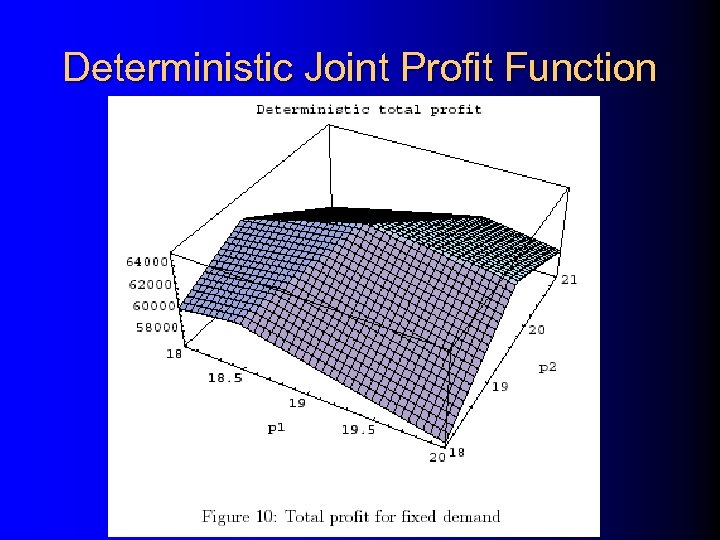Deterministic Joint Profit Function

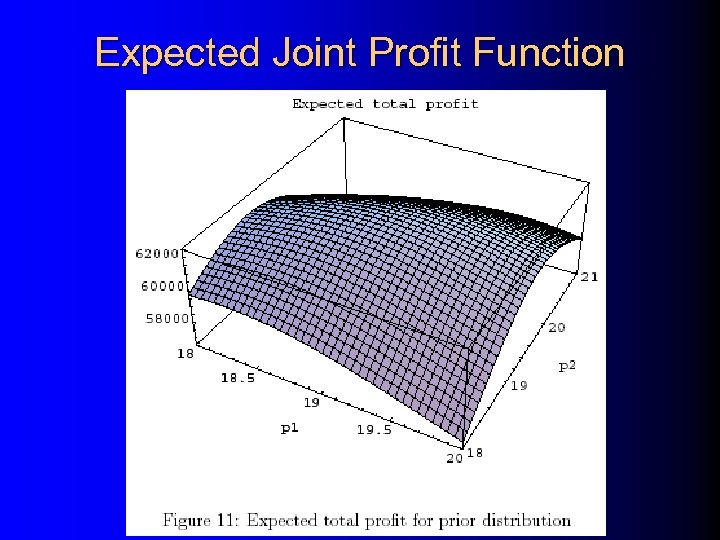Expected Joint Profit Function

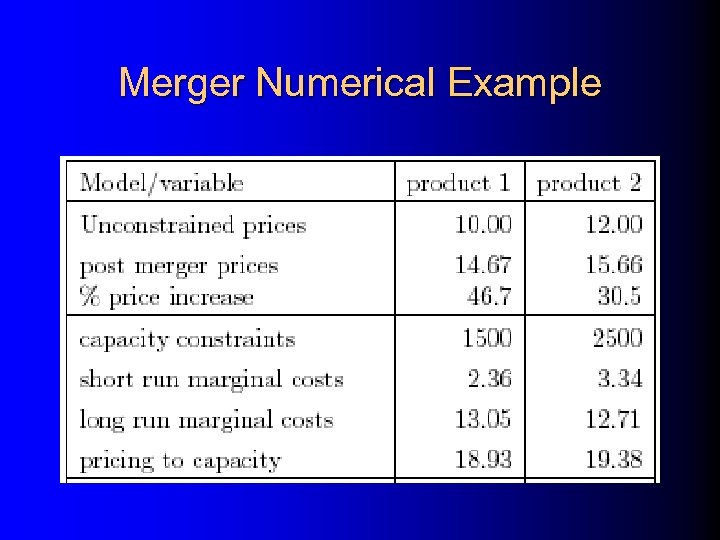Merger Numerical Example

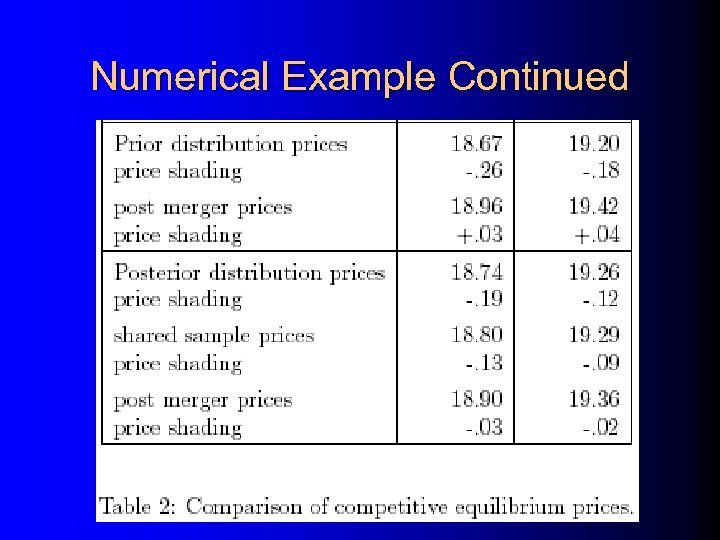Numerical Example Continued

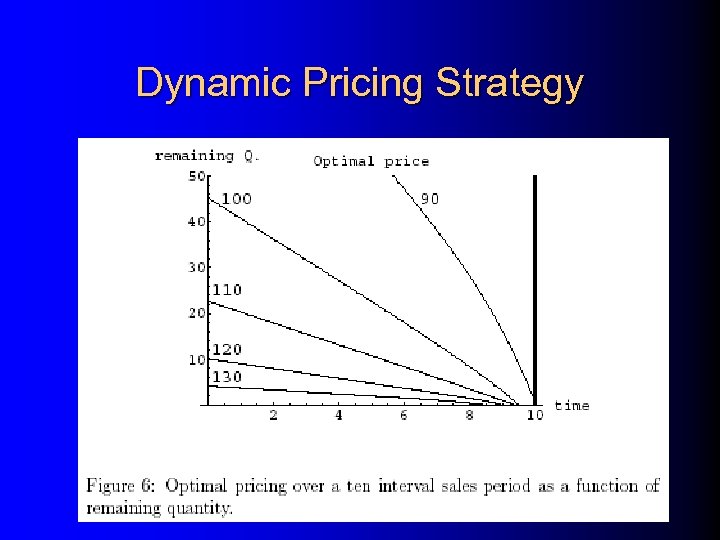Dynamic Pricing Strategy

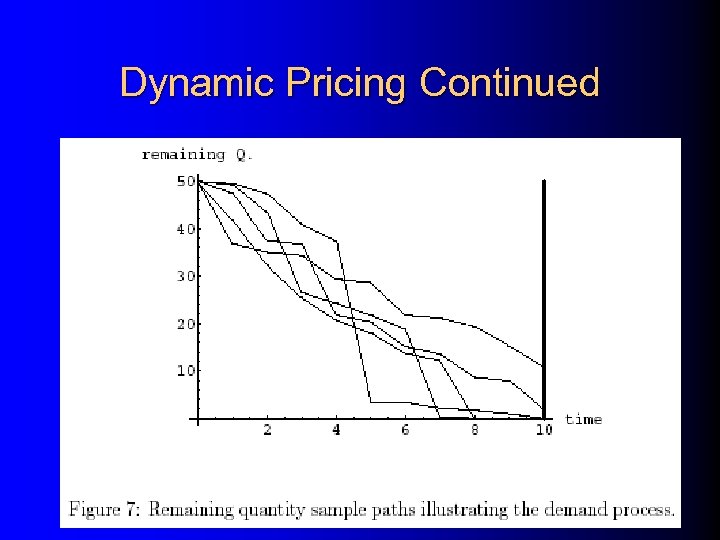Dynamic Pricing Continued

Conclusions Based on Examples • Two merger effects • Ownership effect raises price • Information sharing effect can raise or lower price, but always increases quantity • Both effects small and disappear as uncertainty decreases • Firms price to fill the ships, and this profit calculus is unaffected by merger Not technically correct, but very close

Open Questions: Conjectures • Can an ownership effect reduce price? • Since dynamic pricing reduces uncertainty, it would also reduce merger effect • Small price discrimination effect

Open Questions: Modeling price discrimination between two customer types • Modeling dynamic price adjustment • Modeling rejections (currently, overbooked passengers go home disappointed) • Instead allow them to switch to unconstrained carriers, if any • Conjecture: effect is likely to be very small • • Estimating or calibrating model to real data

Issues in Demand Estimation Luke Froeb Owen Graduate School of Management Vanderbilt University

Typical Example • • Estimate AIDS demand using scanner data Instruments • None needed for weekly data LR vs. SR elasticities (Nevo & Hendel) • Prices in other cities Correlated through costs • Results • High variance • Inelastic demand? • Goods are complements?

Implementation Critique: Too Many Parameters • AIDS has too many parameters • Confidence intervals very wide • Elasticities for merging products is most important • High variance estimator • Alternatives: logit, nested logit, PD GEV (Bresnahan and Stern), mixed logit (BLP) + census data (Nevo) • In these forms, all goods are substitutes • Lower variance, but possible bias

PD GEV, Bresnahan, et al. , i. e. , “Non Nested” Logit • Multiple dimensions of differentiation • Dimensions not nested • On technological frontier or not • Branded or not • Example: Goods 1 & 2 have a trait, but not 3 & 4

Restricted Demand Forms Always yields a postmerger price increase • Parties reluctant to admit even small price increase • If we are going to use these tools to evaluate mergers, must adopt different safe harbors e. g. , by “granting” small MC reduction •

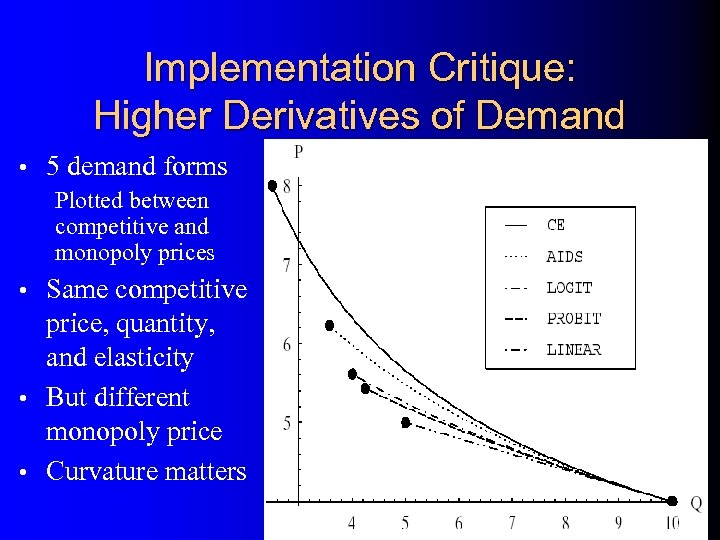Implementation Critique: Higher Derivatives of Demand • 5 demand forms Plotted between competitive and monopoly prices Same competitive price, quantity, and elasticity • But different monopoly price • Curvature matters •

Implementation Critique: Higher Derivatives of Demand • f(x), f'(x), and f"(x) influence predicted price rise • Need location, velocity, and acceleration, • But observe only location • If we cannot estimate f"(x) • Do sensitivity analysis or linear or logit extrapolation to be conservative • Compensating marginal cost reductions don’t depend on acceleration • MC reductions sufficient to offset price increase • Use as a benchmark against which to evaluate efficiency claims

Mergers in Auction Markets Luke Froeb Owen Graduate School of Management Vanderbilt University

Second Price, Private Value, Auction Framework • Example: • Private values are {1, 2, 3, 4, 5, 6} • Merger between {5, 6} reduces price to 4 • Mergers between other bidders have no effect • Price effects of mergers depend on • Frequency of 1 -2 finish (proportional to shares) • Price change to third highest value (proportional to variance)

Simple Functional Form • Model Asymmetry by allowing different bidders to take different numbers of draws Fi(x) = [F (x)]s bidder i takes s draws Winning probabilities are proportionate to the number of draws, and bigger firms win at better prices • When firms merge, the merged firm gets as many draws as the merging firms took •

Bidding for Timber Variable Coefficient Standard $/mbf Error Hauling Miles – 2. 08 0. 48 SBA Status 71. 63 16. 90 Spread Parameter 39. 66 4. 66

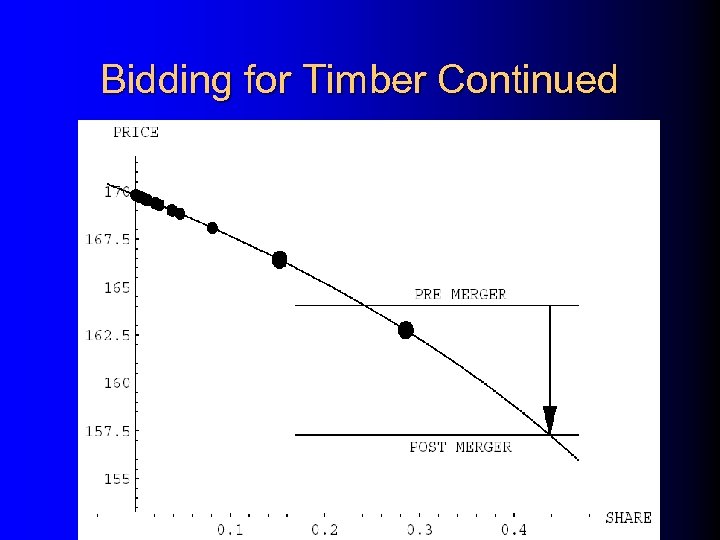Bidding for Timber Continued

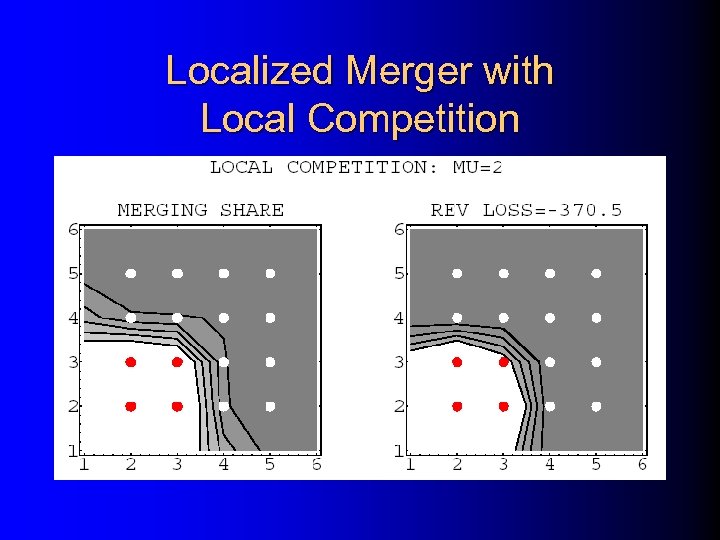Localized Merger with Local Competition

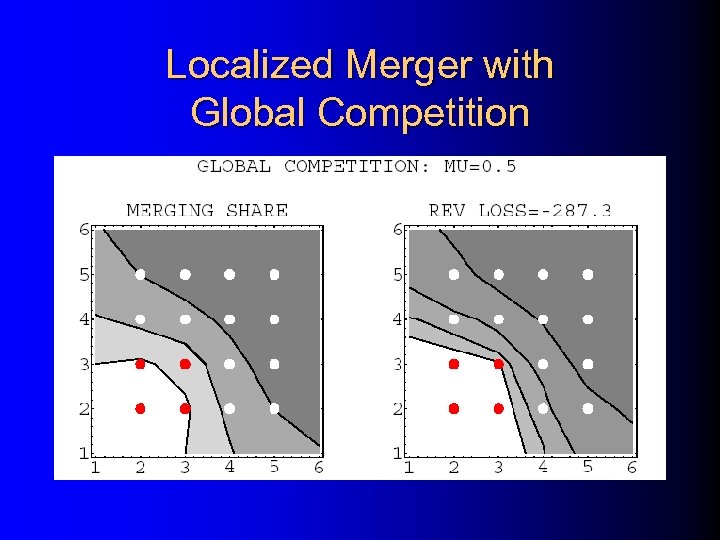Localized Merger with Global Competition

Global Merger with Local Competition

Global Merger with Global Competition

Auction Summary • The price effects of mergers depend on • Location of merging and nonmerging bidders • Location of tracts • Whether competition is “global” or “local” i. e. , whether transport costs are high relative to variance of values. • In general, unilateral are smaller than with price or quantity competition But collusion may be more of a risk

Vertical Relationships Luke Froeb Owen Graduate School of Management Vanderbilt University

Horizontal Mergers and Vertical Restraints Joint work with Steven Tschantz (Math Dept. ) and Gregory Werden (U. S. Department of Justice) • Horizontal mergers • • Relative consensus on how to model horizontal restraints— coordinated and unilateral effects • Policy debate is empirical • Vertical restraints • No consensus on how to model vertical restraints • Policy debate is theoretical or on “necessary conditions, ” e. g. , market share screens

Questioning the Consensus on Horizontal Merger Effects How do vertical restraints affect the standard horizontal merger analysis, which ignores retail sector? • Assuming we have a good vertical theory, can we estimate harm from vertical restraints? •

Monopoly Retail Sector on Top of Bertrand Manufacturing Sector • Strategic bargaining game (n +1 players) Upstream Bertrand oligopolists (n) make take it or leave it offers to retail monopolist Retailer chooses the best set of offers • Then, two upstream manufacturers merge • Effect of merger is the difference between the pre and postmerger equilibria • What happens to retail prices and quantities?

Results: The Retail Sector Matters a Lot • Upstream horizontal mergers can have a variety of effects when “filtered” through retail sector • Transparent retail sector Merger effect same as if retail sector ignored • Opaque retail sector No merger effect • Double marginalization Can amplify OR attenuate merger effects

Three Different Games • Game 1: retailer must carry all profitable products Result: Transparent retail sector • Game 2: retailer has option of exclusive dealing Result: Opaque retail sector • Game 3: manufacturers limited to offering wholesale unit prices independent of quantity Result: Double marginalization, which can amplify or attenuate merger effects

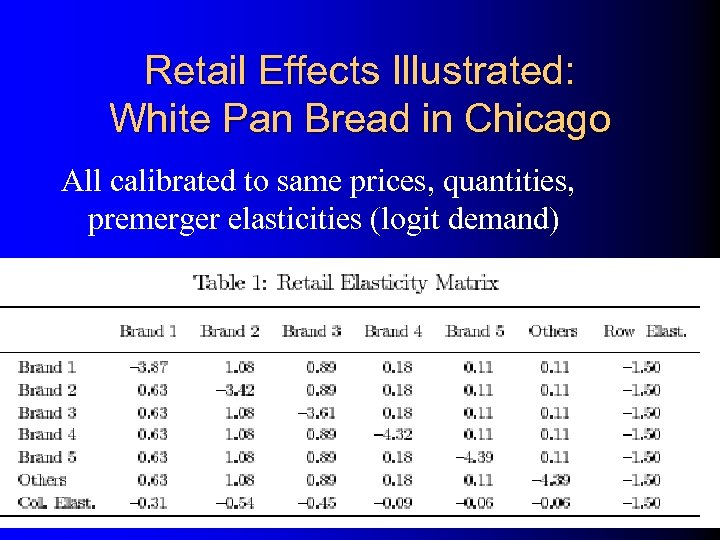Retail Effects Illustrated: White Pan Bread in Chicago All calibrated to same prices, quantities, premerger elasticities (logit demand)

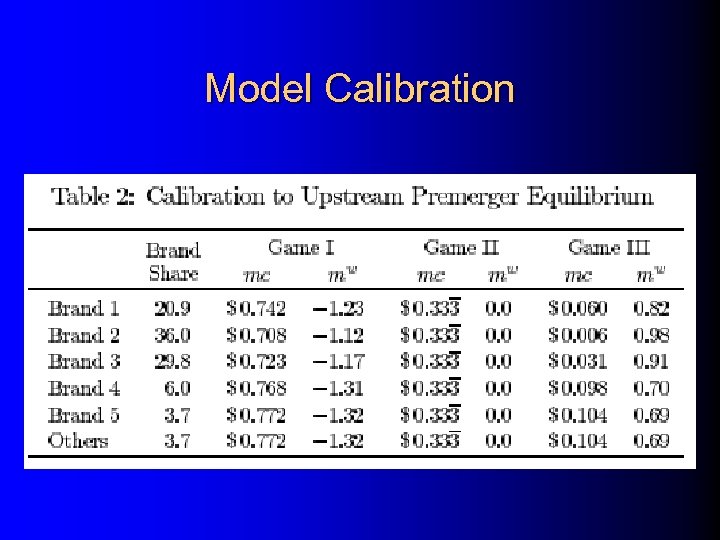Model Calibration

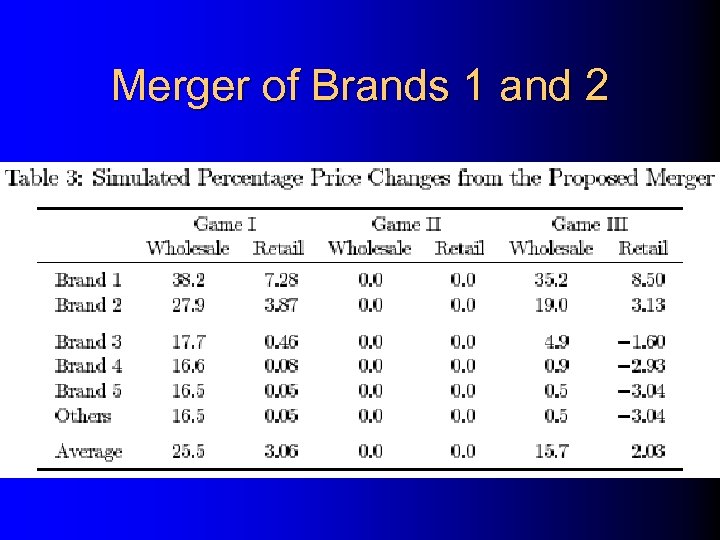Merger of Brands 1 and 2

Conclusions • Retail sector can matter a lot in horizontal merger analysis • Constant percentage markup usually assumed, which is transparent case • Not correct if actual case is “opaque” or “double marginalization” • Empirical identification of retail game • Games have negative, zero, and positive wholesale margins, respectively

Unanswered Questions • How do retailer’s behave? • Vendor managed inventory • Complex nonlinear contracts with promotional allowances, quantity discounts: Is two part pricing a good metaphor? • The n by k case (n mfgs, k retailers) • Retailers compete on selection, price, convenience • Does opaque equilibrium hold for n by k case?

Damages from Vertical Restraints • Two actual cases: • US v. Dentsply, controlled distribution channel • Private case, firm favored its own retail arm with lower prices • Questions raised: • How much does distribution channel or MC affect the price setting equilibrium? • How much more profit would the injured firms have made absent the vertical restraints?