Quanta ciphers and computers Artur Ekert The

Quanta, ciphers and computers Artur Ekert

The Gambling Scholar Girolamo Cardano described himself as "Hot-tempered, single-minded, and given to women, “… "cunning, crafty, sarcastic, diligent, impertinent, sad, treacherous, magician and sorcerer, miserable, hateful, lascivious, obscene, lying, obsequious, " and "fond of the prattle of old men. " 1501 -1576

Two ingredients of quantum theory probability written 1524 Liber de Ludo Aleae (The Book of Games of Chance) complex numbers written circa 1545

Complex numbers Niccolo Fontana Tartaglia The oath sworn by Cardan (according to Tartaglia) I swear to you, by God's holy Gospels, and as a true man of honour, not only never to publish your discoveries, if you teach me them, but I also promise you, and I pledge my faith as a true Christian, to note them down in code, so that after my death no one will be able to understand them.

Classical versus Quantum PROBABILITIES AMPLITUDES

It does make a difference Interference term

You can observe quantum interference 0 1 1 0 0 1 © Centre for Quantum Technologies, Singapore

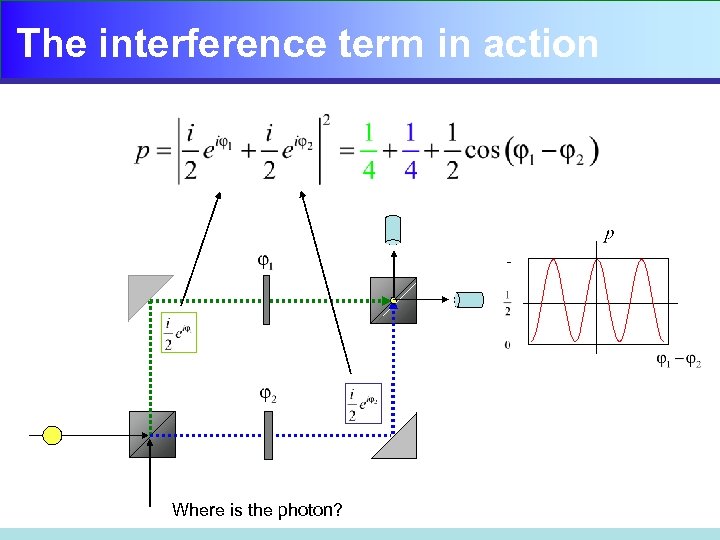The interference term in action Where is the photon?

Bookkeeping of probs and amps stochastic unitary

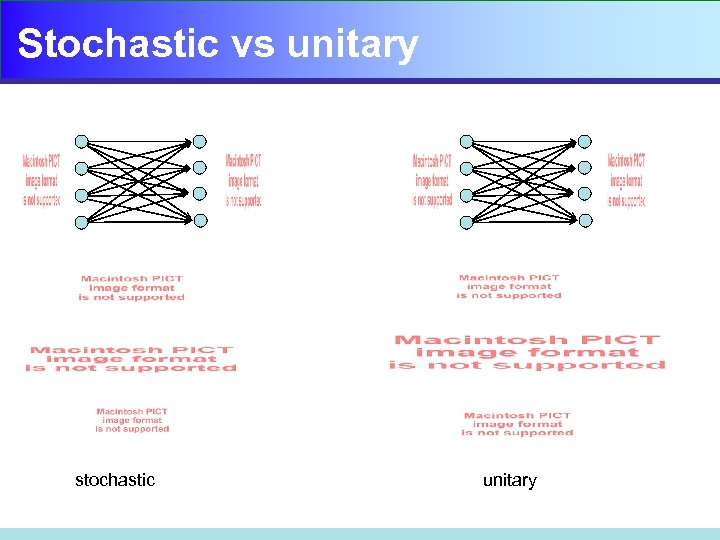Stochastic vs unitary stochastic unitary

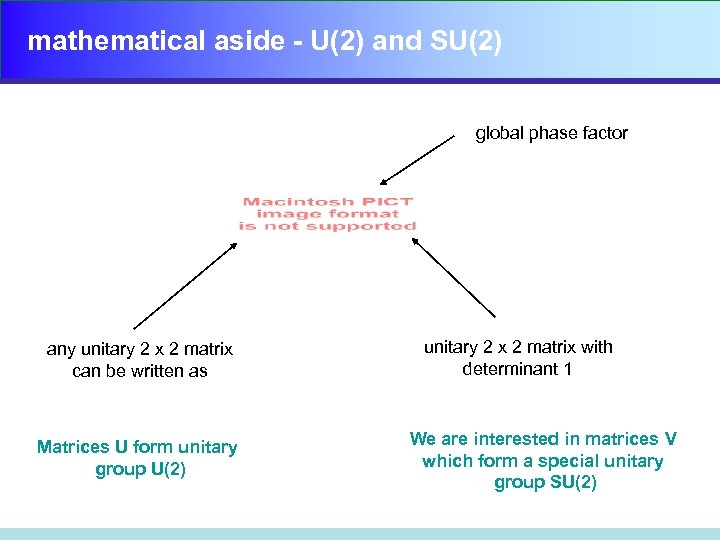mathematical aside - U(2) and SU(2) global phase factor any unitary 2 x 2 matrix can be written as Matrices U form unitary group U(2) unitary 2 x 2 matrix with determinant 1 We are interested in matrices V which form a special unitary group SU(2)

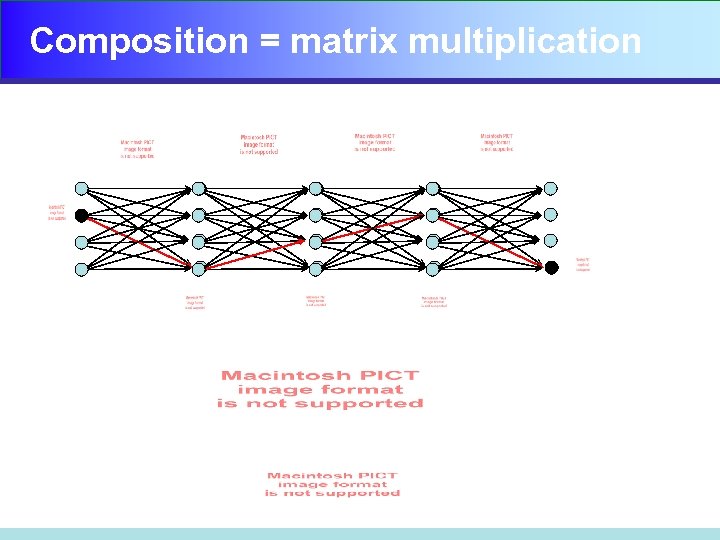Composition = matrix multiplication

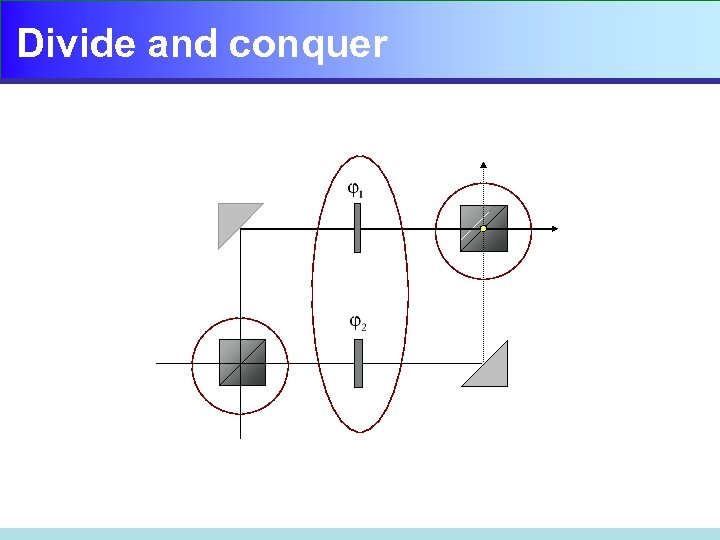Divide and conquer

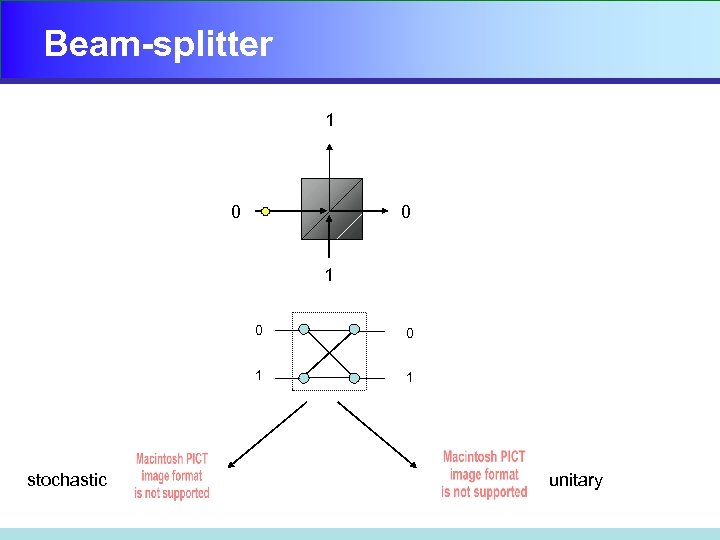Beam-splitter 1 0 0 1 stochastic 0 1 unitary

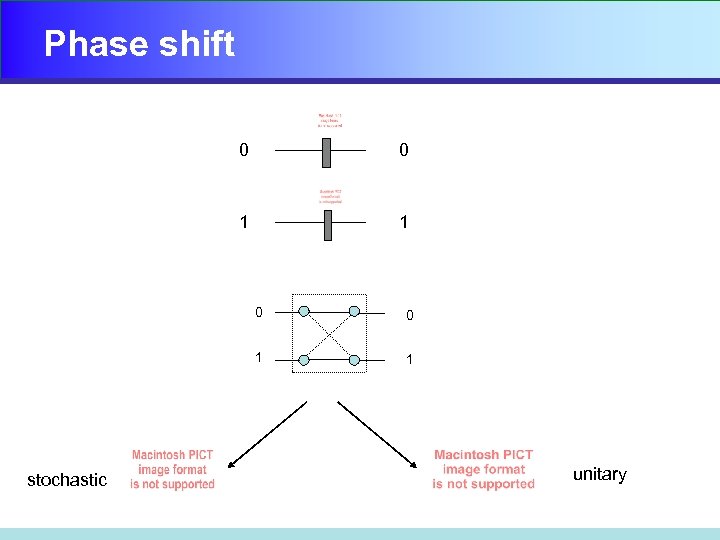Phase shift 0 0 1 1 0 1 stochastic 0 1 unitary

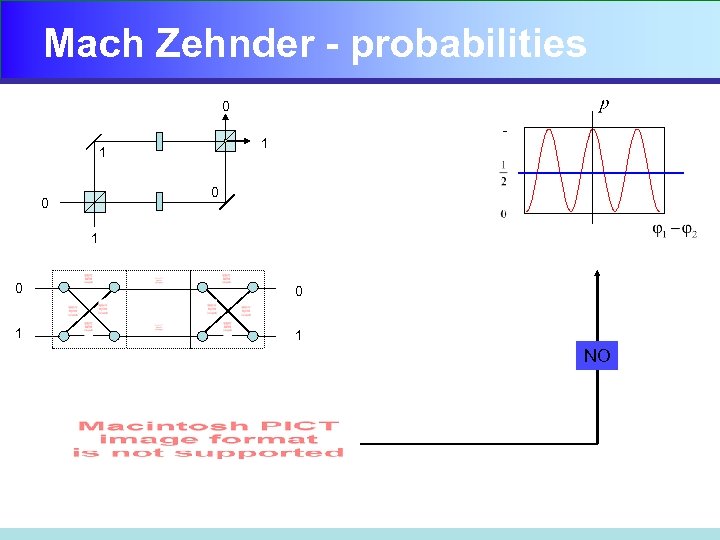Mach Zehnder - probabilities 0 1 1 0 0 1 1 NO

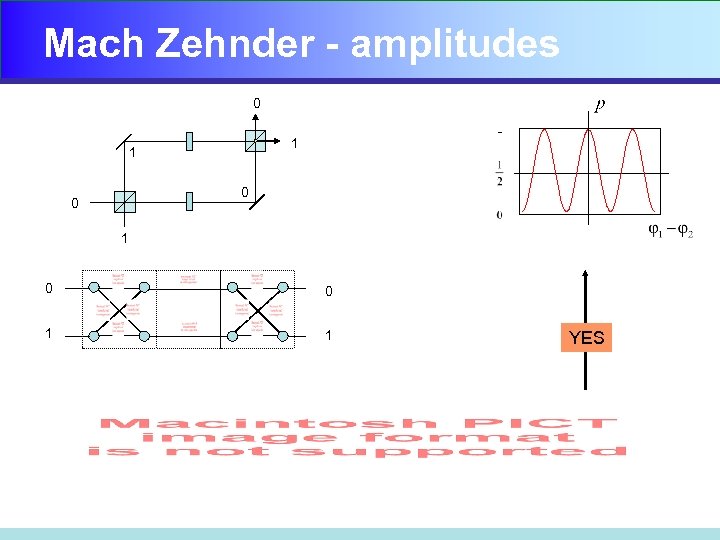Mach Zehnder - amplitudes 0 1 1 0 0 1 1 YES

Amplitudes & probabilities amplitudes

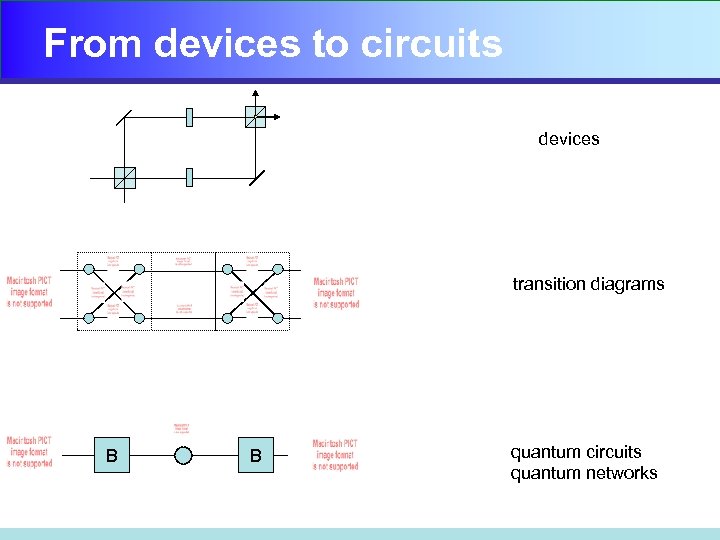From devices to circuits devices transition diagrams B B quantum circuits quantum networks

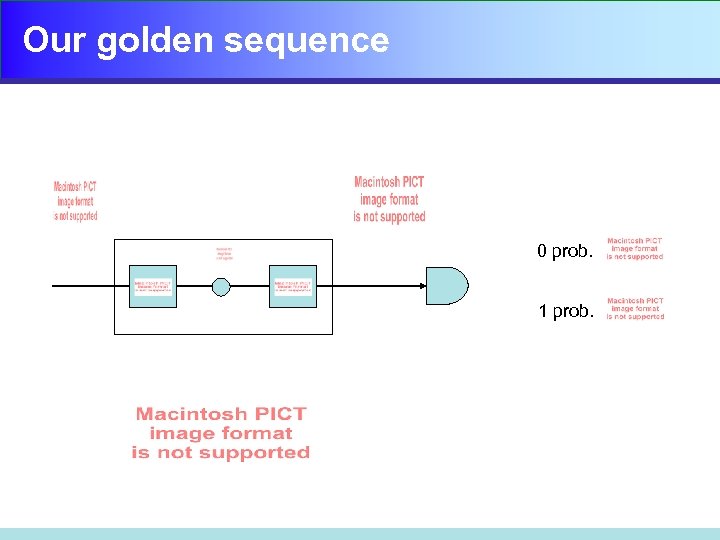Our golden sequence 0 prob. 1 prob.

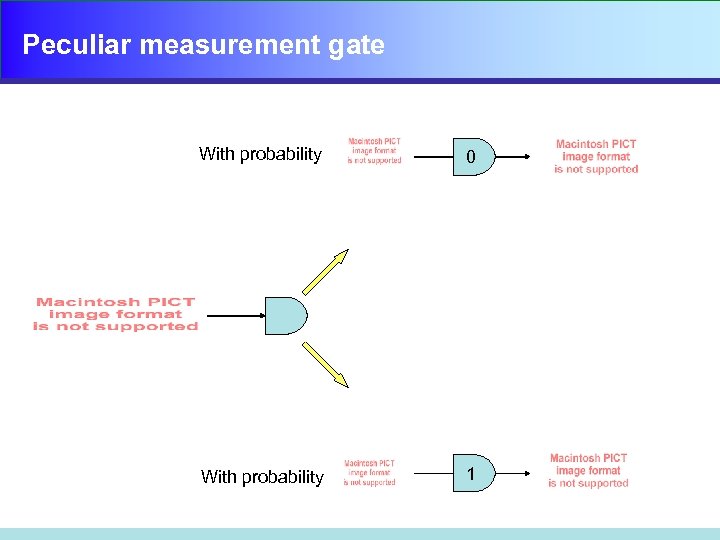Peculiar measurement gate With probability 0 With probability 1

It may look like this… …with neutrons… © Lauren Hellig With photons… © NIST Boulder

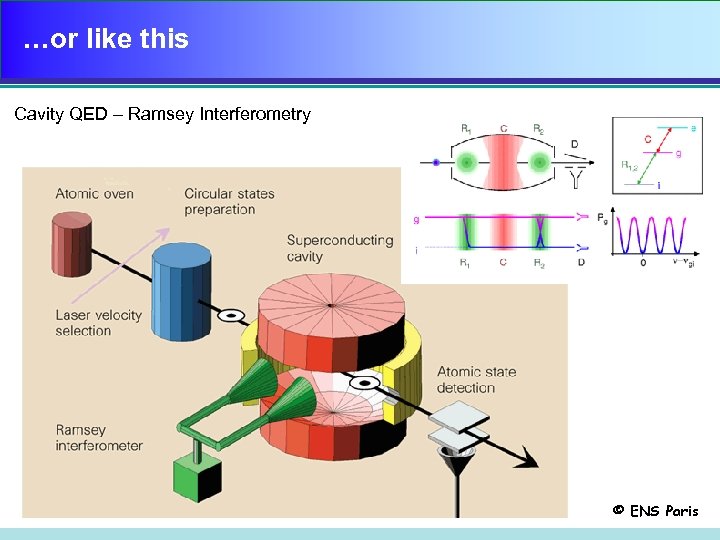…or like this Cavity QED – Ramsey Interferometry © ENS Paris

More precisely like this © ENS Paris

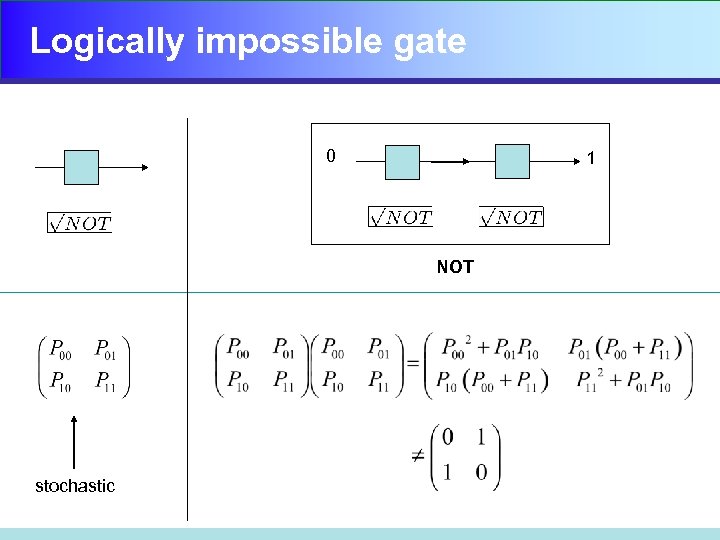Logically impossible gate 0 1 NOT stochastic

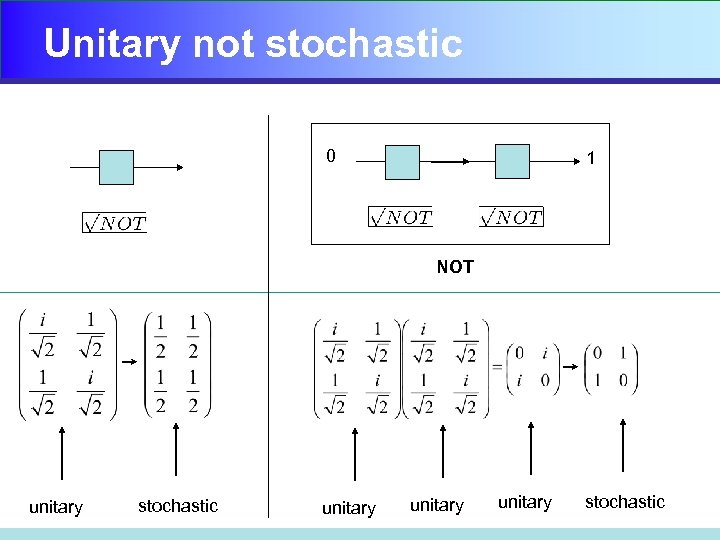Unitary not stochastic 0 1 NOT unitary stochastic unitary stochastic

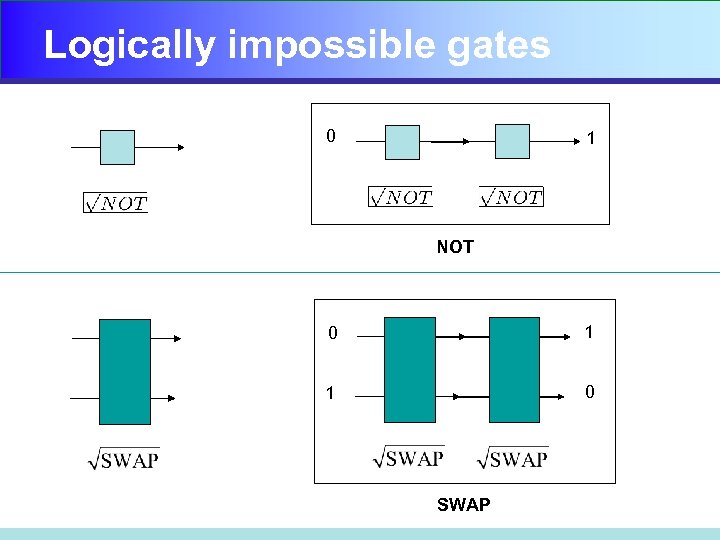Logically impossible gates 0 1 NOT 0 1 1 0 SWAP

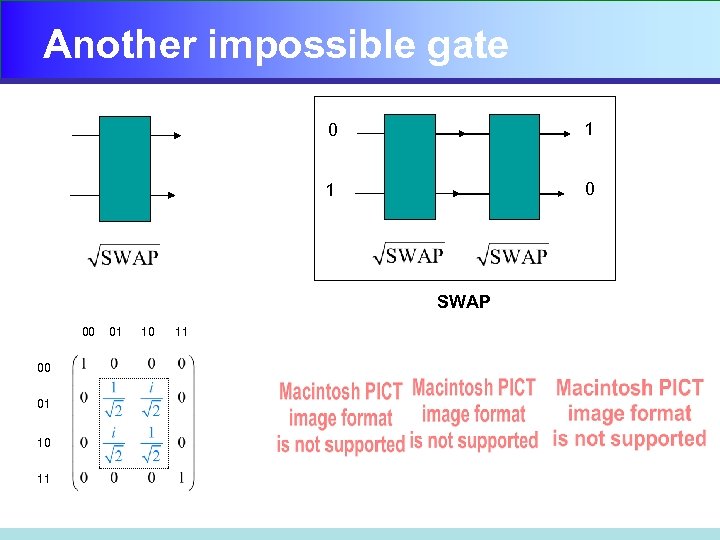Another impossible gate 0 1 1 0 SWAP 00 00 01 10 11

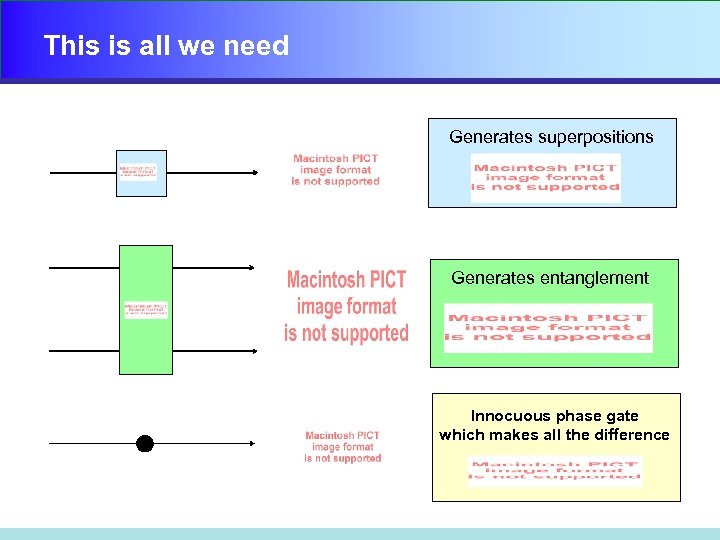This is all we need Generates superpositions Generates entanglement Innocuous phase gate which makes all the difference

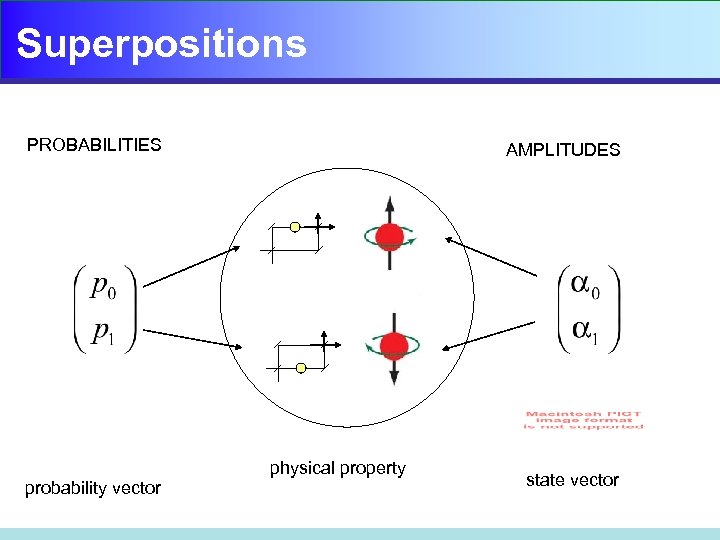Superpositions PROBABILITIES probability vector AMPLITUDES physical property state vector

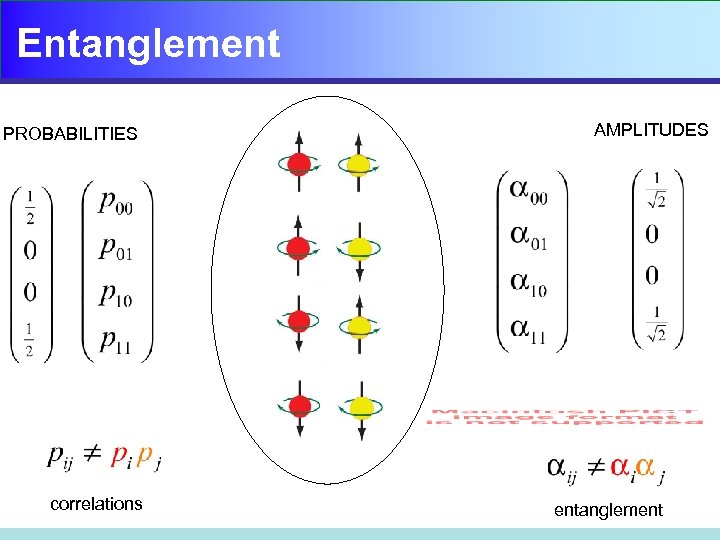Entanglement PROBABILITIES correlations AMPLITUDES entanglement

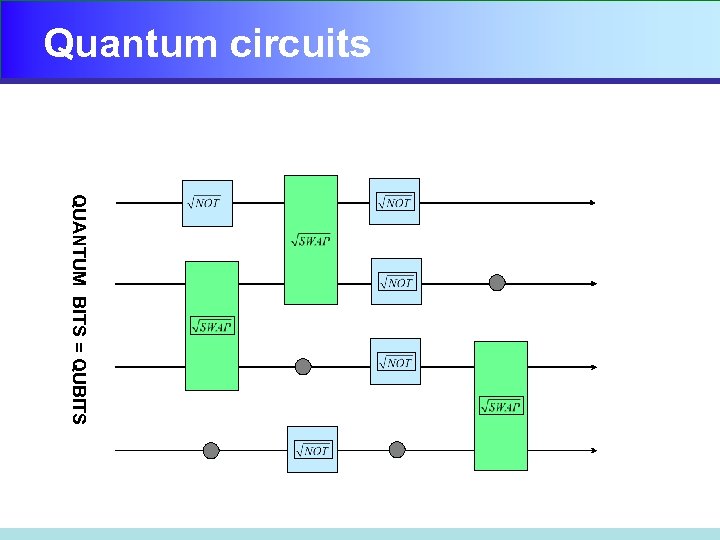Quantum circuits QUANTUM BITS = QUBITS

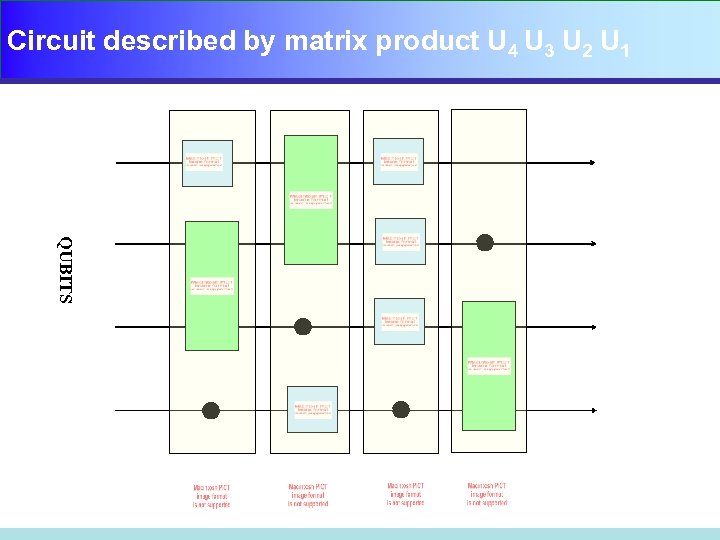Circuit described by matrix product U 4 U 3 U 2 U 1 QUBITS

But what kind of unitary is this? How to express this 16 x 16 matrix in terms of matrices

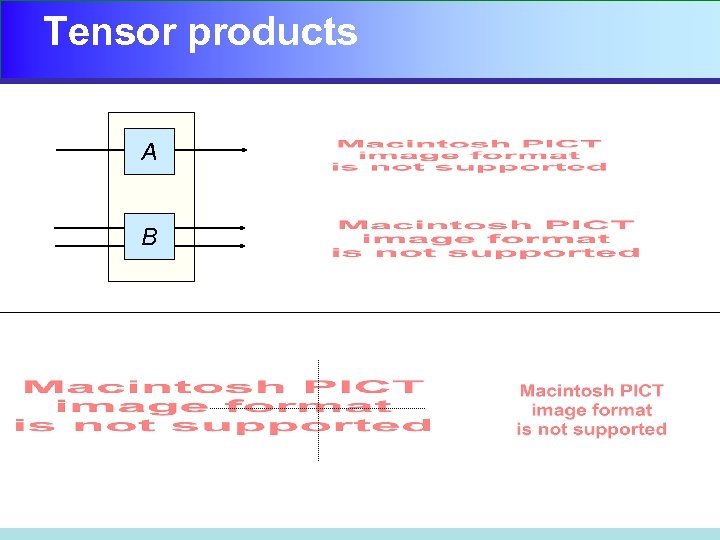Tensor products A B

Entanglement again SEPARABLE ENTANGLED

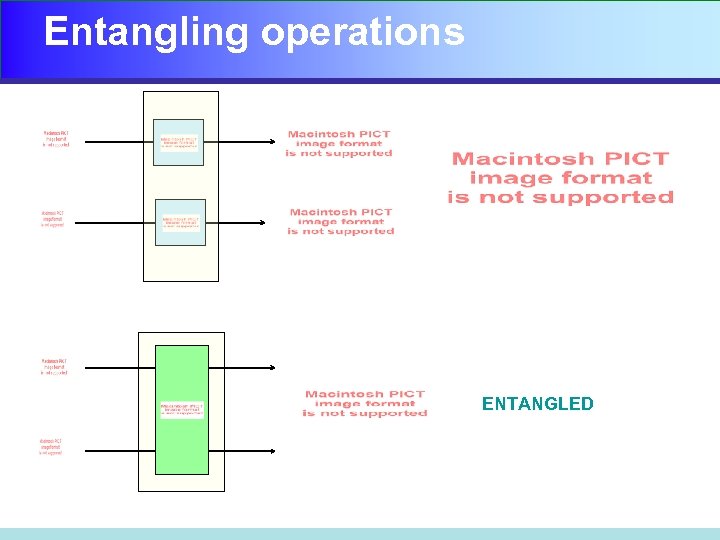Entangling operations ENTANGLED

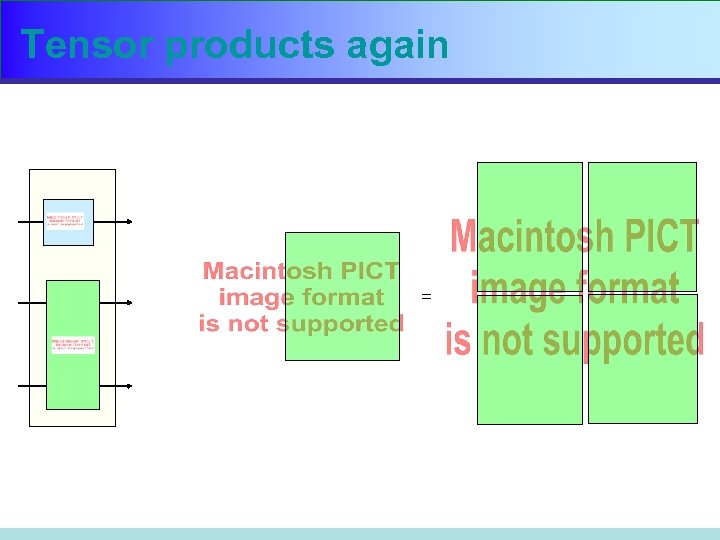Tensor products again =

and again

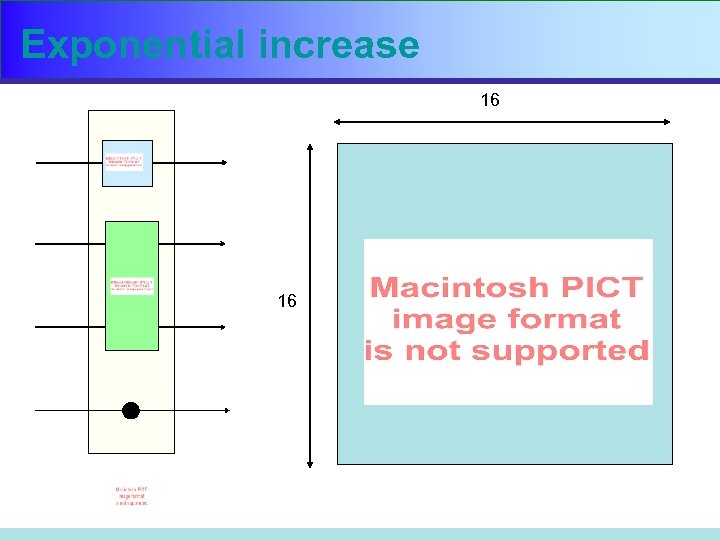Exponential increase 16 16

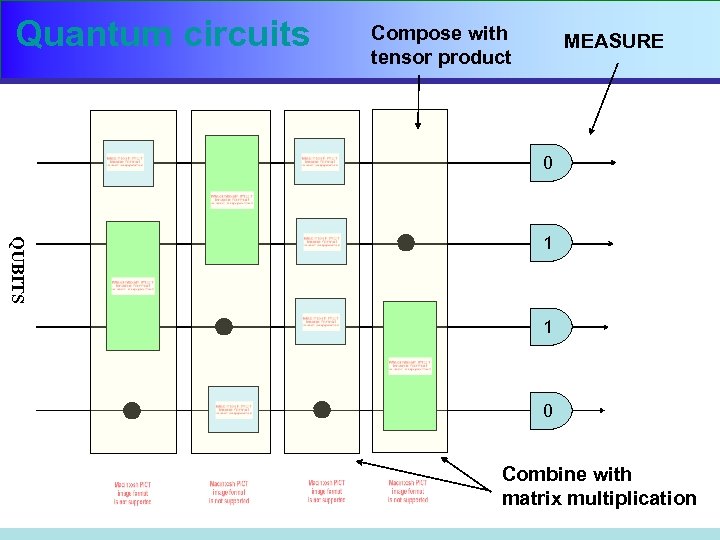Quantum circuits Compose with tensor product MEASURE 0 QUBITS 1 1 0 Combine with matrix multiplication

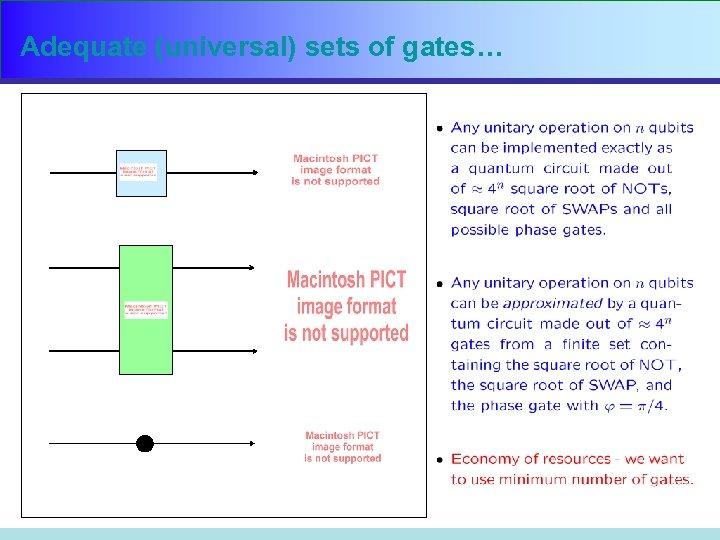Adequate (universal) sets of gates…

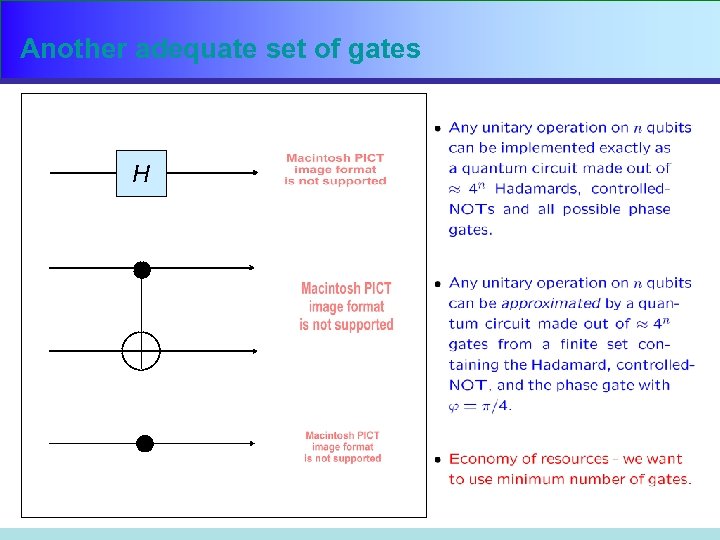Another adequate set of gates H

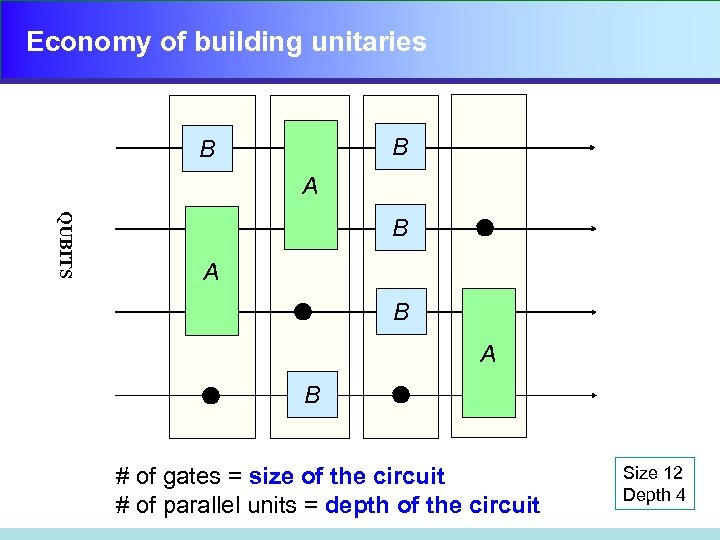Economy of building unitaries B B A QUBITS B A B # of gates = size of the circuit # of parallel units = depth of the circuit Size 12 Depth 4

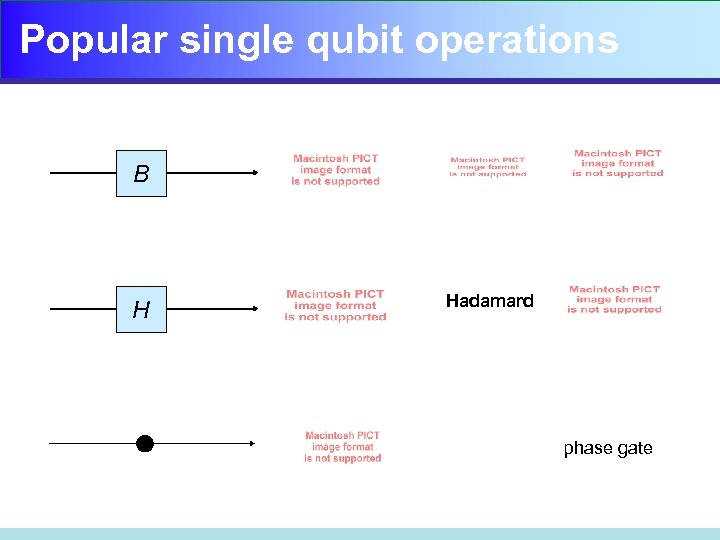Popular single qubit operations B H Hadamard phase gate

Pauli matrices conventional notation X “bit flip” Y Z “phase flip”

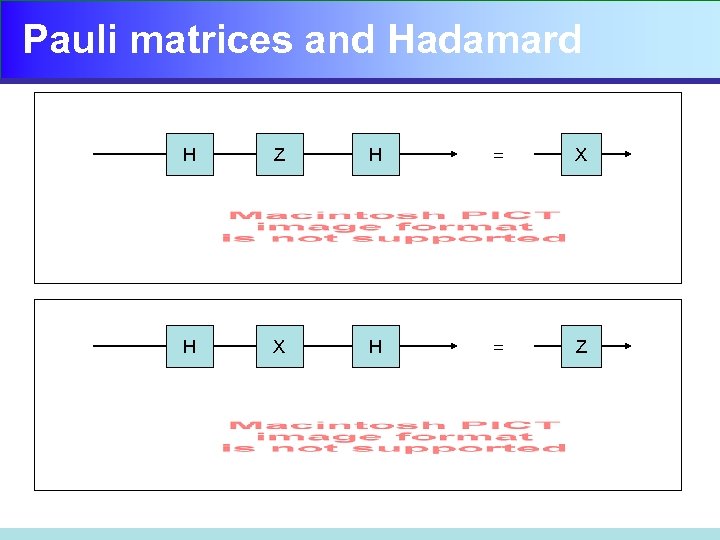Pauli matrices and Hadamard H Z H = X H = Z

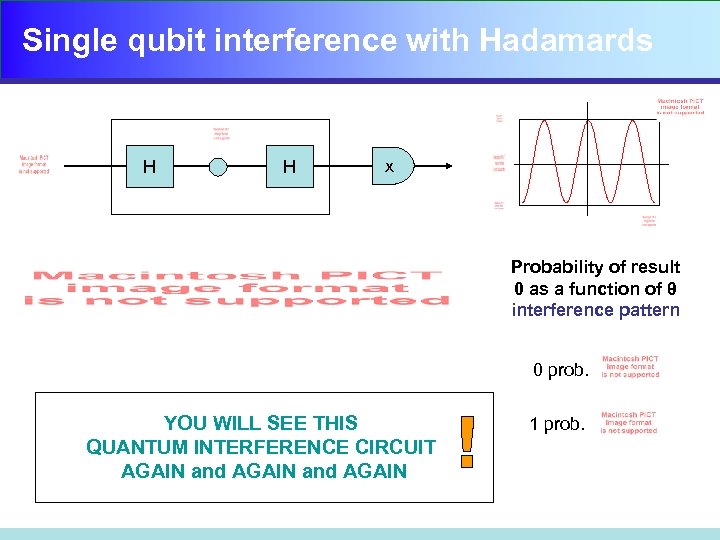Single qubit interference with Hadamards H H x Probability of result 0 as a function of θ interference pattern 0 prob. YOU WILL SEE THIS QUANTUM INTERFERENCE CIRCUIT AGAIN and AGAIN 1 prob.

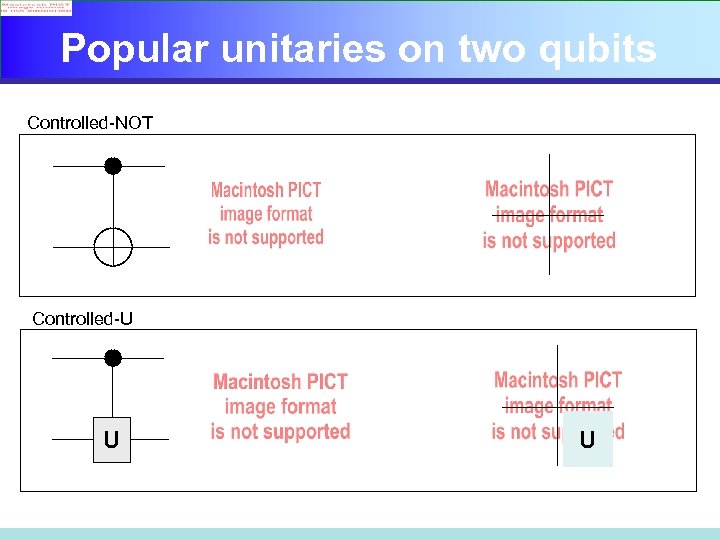Popular unitaries on two qubits Controlled-NOT Controlled-U U U

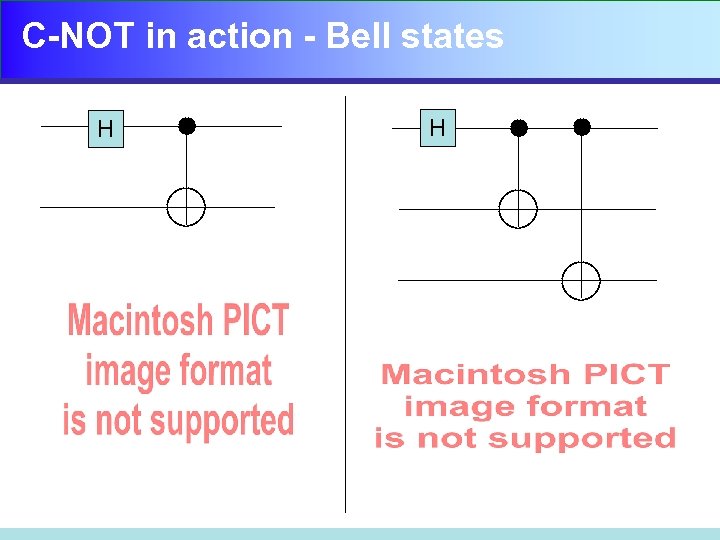C-NOT in action - Bell states H H

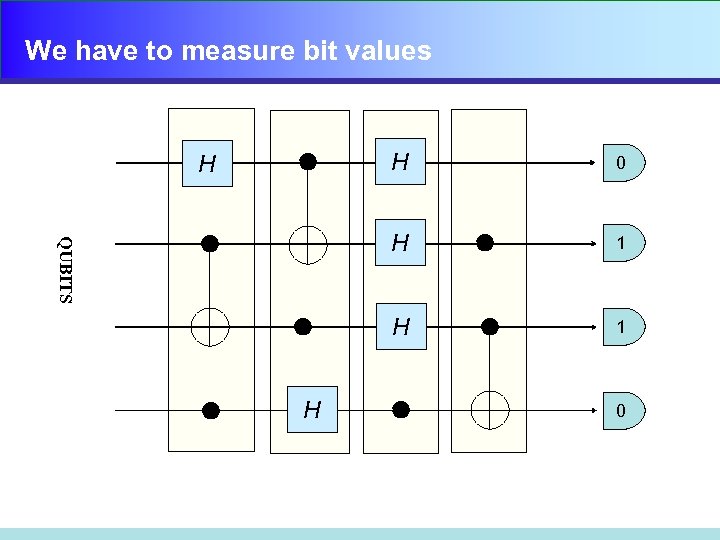We have to measure bit values H QUBITS 1 H H 0 H H 1 0

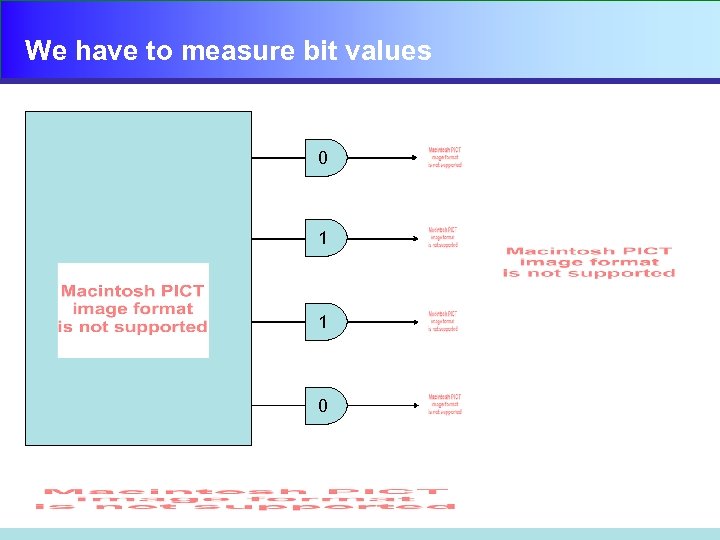We have to measure bit values 0 1 1 0

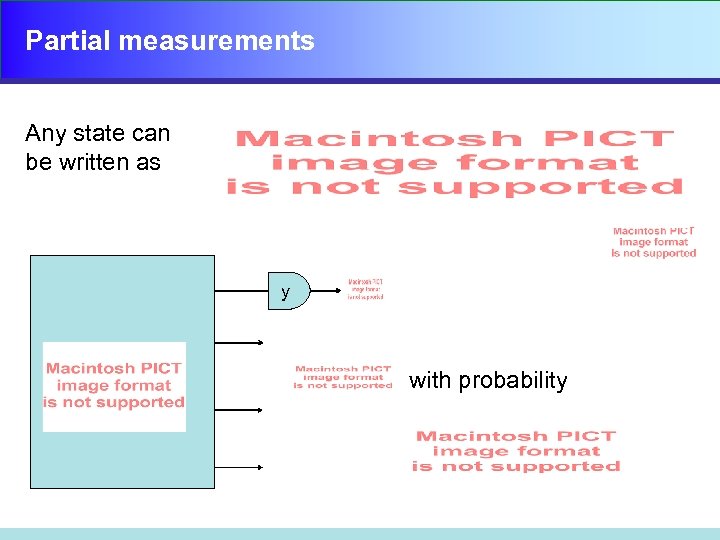Partial measurements Any state can be written as y with probability

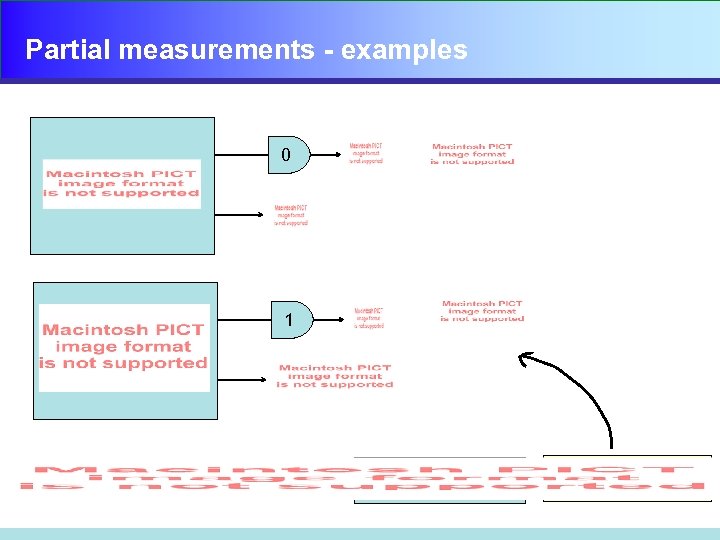Partial measurements - examples 0 1

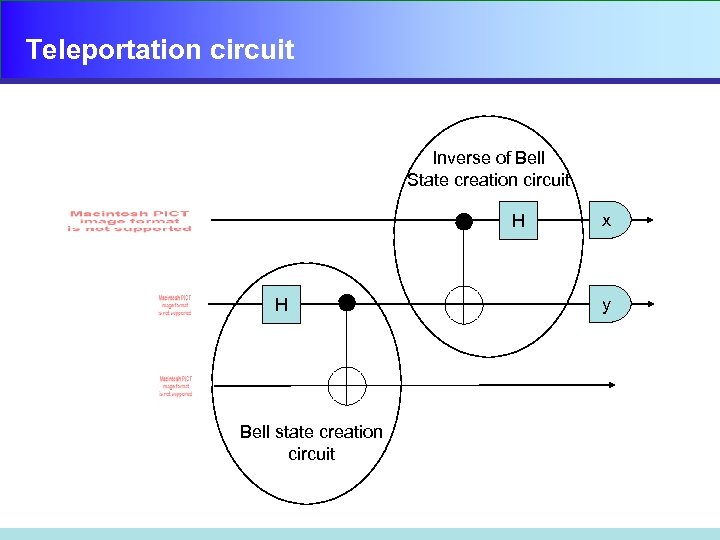Teleportation circuit Inverse of Bell State creation circuit H H Bell state creation circuit x y

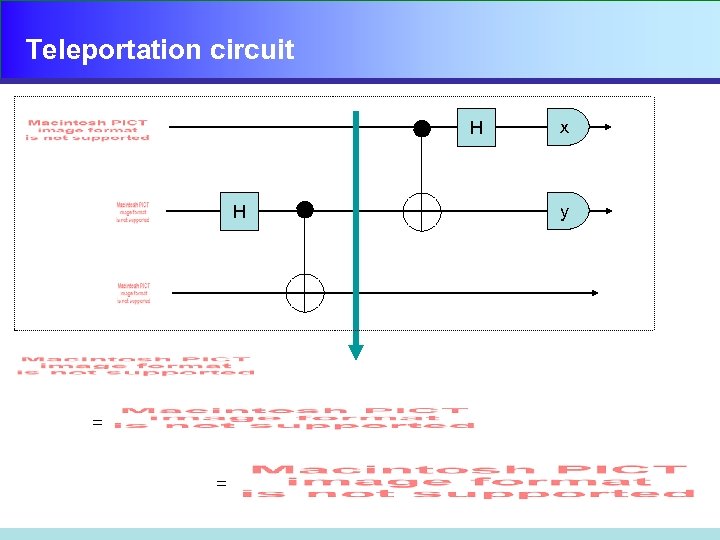Teleportation circuit H H = = x y

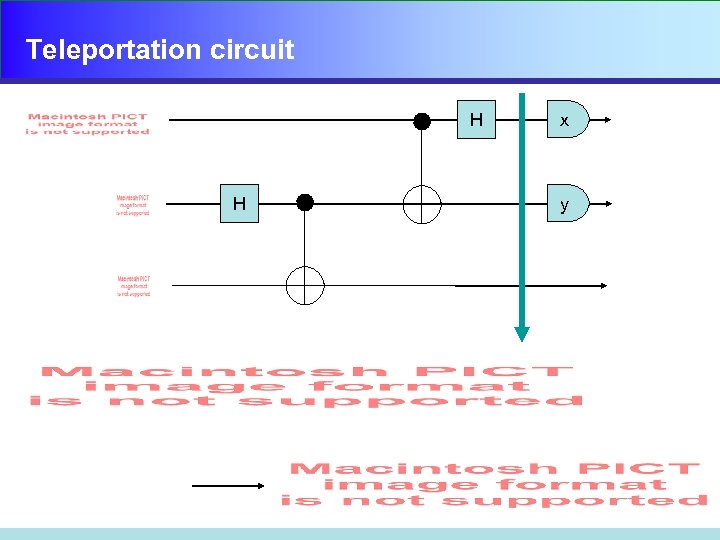Teleportation circuit H H x y

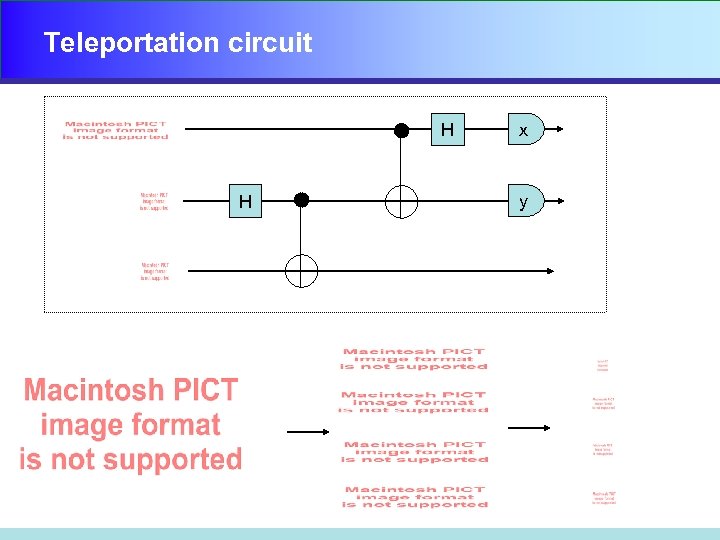Teleportation circuit H H x y

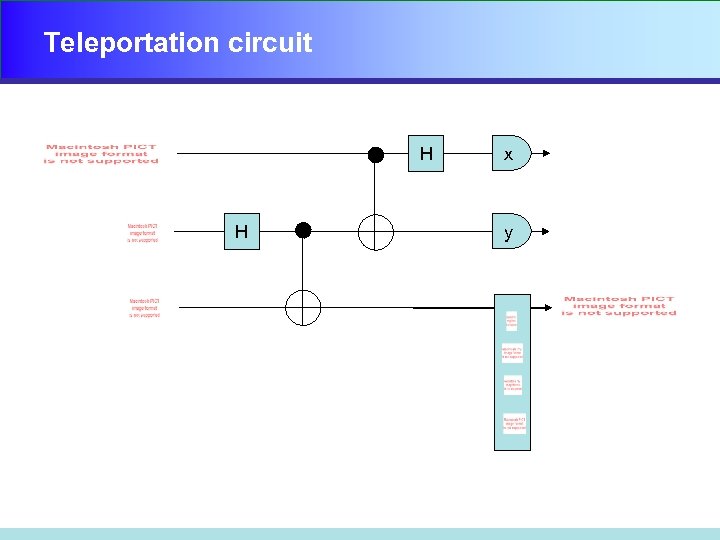Teleportation circuit H H x y

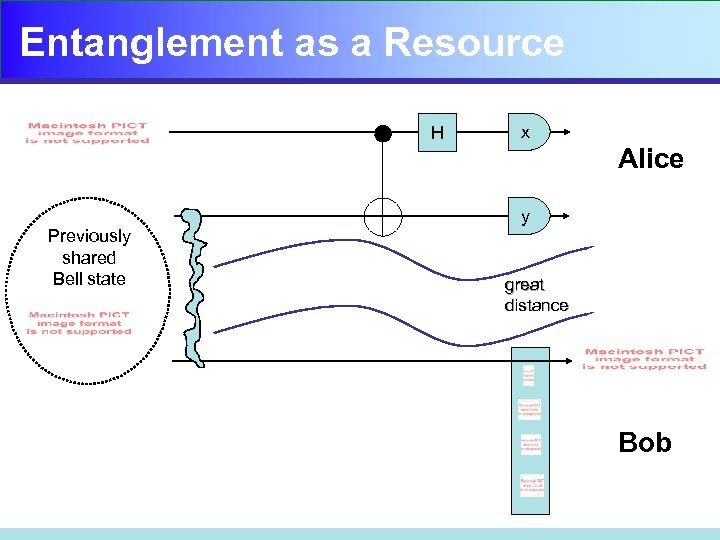Entanglement as a Resource H x Alice Previously shared Bell state y great distance Bob

Schrödinger’s idea Manuscript by Schrödinger dated back to 1932 or 1933. Discovered by Matthias Christandl and Lawrence Ioannou of Cambridge University in the Schrödinger archive in Vienna.

Generating entanglement Violet Laser Diode BBO crystal Centre for Quantum Technologies, Singapore