QUADRILATERALS: HOW DO WE SOLVE THEM? By: Steve Kravitsky & Konstantin Malyshkin
AIM: HOW DO WE SOLVE PROOFS OF QUADRILATERALS? Homework: Textbook Page – 261, Questions 1 -5 Do Now: What are the two groups that quadrilaterals break off into? Quadrilaterals Parallelogram Trapezoid
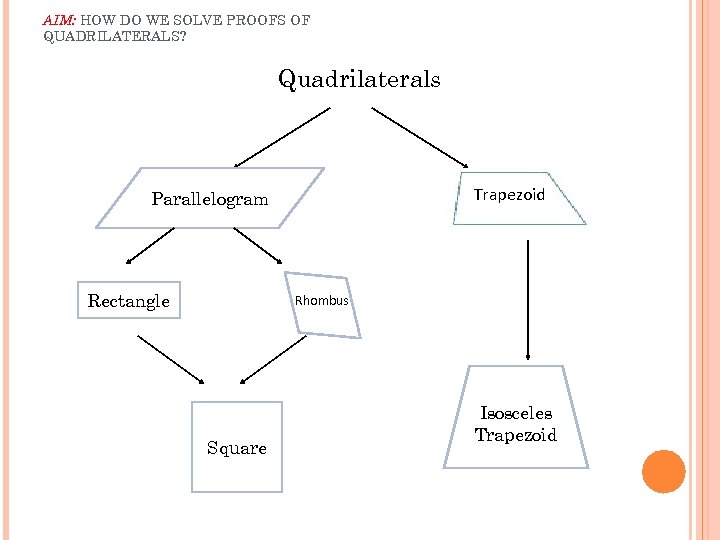
AIM: HOW DO WE SOLVE PROOFS OF QUADRILATERALS? Quadrilaterals Trapezoid Parallelogram Rectangle Rhombus Square Isosceles Trapezoid
AIM: HOW DO WE SOLVE PROOFS OF QUADRILATERALS? Properties of a Parallelogram: Properties of a Square: 1. All rectangle properties 1. Both pairs of opposite sides are parallel 2. Both pairs of opposite sides are congruent 2. All rhombus properties 3. Both pairs of opposite angles are congruent 4. Consecutive angles are congruent 5. A diagonal divides it into two congruent triangles 6. The diagonals bisect each other. Properties of a Rectangle: 1. All six parallelogram properties 2. All angles are right angles 3. The diagonals bisect each others Properties of a Rhombus: 1. All six parallelogram properties 2. All four sides are congruent 3. The diagonals bisect the angles 4. The diagonals are perpendicular to each other
AIM: HOW DO WE SOLVE PROOFS OF QUADRILATERALS? Properties of a Trapezoid: 1. Exactly one pair of parallel sides Properties of a Isosceles Trapezoid: 1. Exactly one pair of parallel sides 2. Non-parallel sides are congruent 3. The diagonals are congruent 4. The base angles are congruent
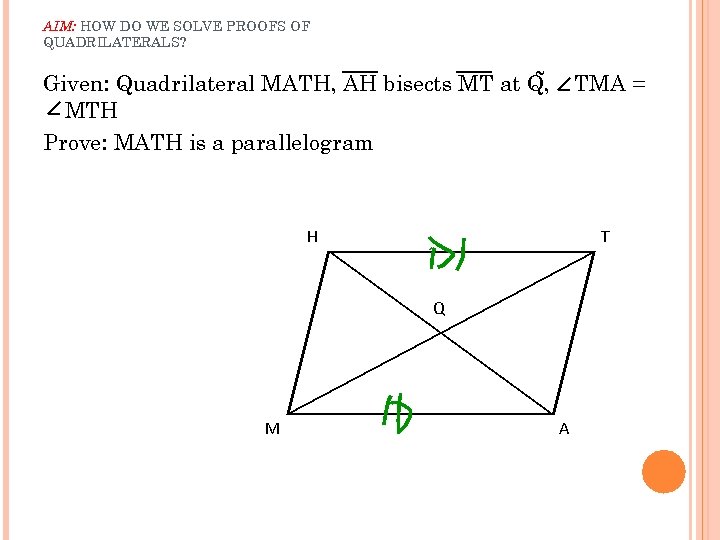
AIM: HOW DO WE SOLVE PROOFS OF QUADRILATERALS? ~ Given: Quadrilateral MATH, AH bisects MT at Q, MTH Prove: MATH is a parallelogram TMA = H T Q M A
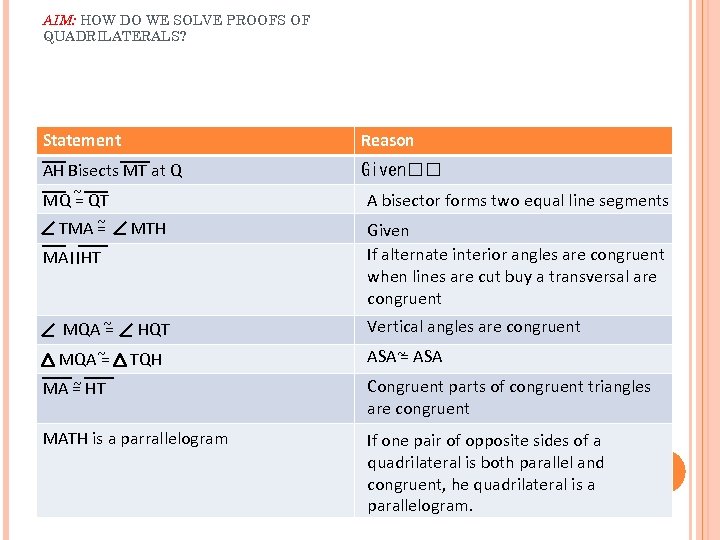
AIM: HOW DO WE SOLVE PROOFS OF QUADRILATERALS? Statement Reason AH Bisects MT at Q MQ ~ QT = Given TMA ~ = MTH MA HT MQA ~ HQT = MQA~ TQH = A bisector forms two equal line segments Given If alternate interior angles are congruent when lines are cut buy a transversal are congruent Vertical angles are congruent ASA ~ ASA = ~ MA = HT Congruent parts of congruent triangles are congruent MATH is a parrallelogram If one pair of opposite sides of a quadrilateral is both parallel and congruent, he quadrilateral is a parallelogram.
AIM: HOW DO WE SOLVE PROOFS OF QUADRILATERALS? Pair Share: Workbook Pages : Page 245, questions 1 -5 Page 232, questions 1 -5 Page 222, questions 17 and 20
Скачать презентацию QUADRILATERALS HOW DO WE SOLVE THEM By Steve
61c09db4c30dbe37e5697347fea64557.ppt