Quadratic Functions and their applications For a

Quadratic Functions… and their applications!

For a typical basketball shot, the ball’s height (in feet) will be a function of time in flight (in seconds), modeled by an equation such as h = -16 t 2 +40 t +6. a) What is the maximum height of the ball? b) When will the shot reach the height of the basket? (10 feet) c) When will the ball hit the floor, if it missed the basket entirely?

a) What is the maximum height of the ball? Ø Put it in your calculator! Ø Use your zooms and change your window until you see the maximum. Ø Find the maximum! Answer: The maximum height of the ball is 31 feet!

b) When will the shot reach the height of the basket? (10 feet) Ø Key words to highlight: When (so we are looking for our x) Height of the basket (10 feet) Ø Put 10 in for y 2 and find the… INTERSECTION! Answer: 2. 4 seconds!

c) When will the ball hit the floor, if it missed the basket entirely? Ø What do we put in for y 2? y 2 = 0 Ø Now find the intersection! Answer: The ball will hit the floor after 2. 64 seconds!

YOU DO: Ø The height, H metres, of a rocket t seconds after it is fired vertically upwards is given by l l l How long does it take for the rocket to reach its maximum height? What is the maximum height reached by the rocket? How long does it take for the rocket to fall back to earth?

Mrs. Holst (who loves to swim!) is putting in a swimming pool next to her house. She wants to put a nice, rectangular privacy fence around it, but she can only afford to pay for 50 feet of fencing. If she does not need a fence on the part adjacent to her house, what are the dimensions of the fence with the largest area she could have for her pool?

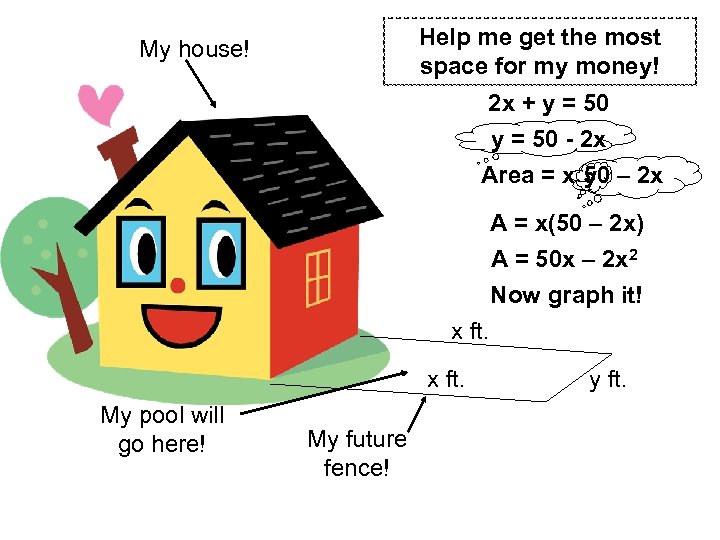Help me get the most space for my money! My house! 2 x + y = 50 - 2 x Area = x 50 – 2 x y A = x(50 – 2 x) A = 50 x – 2 x 2 Now graph it! x ft. My pool will go here! My future fence! y ft.

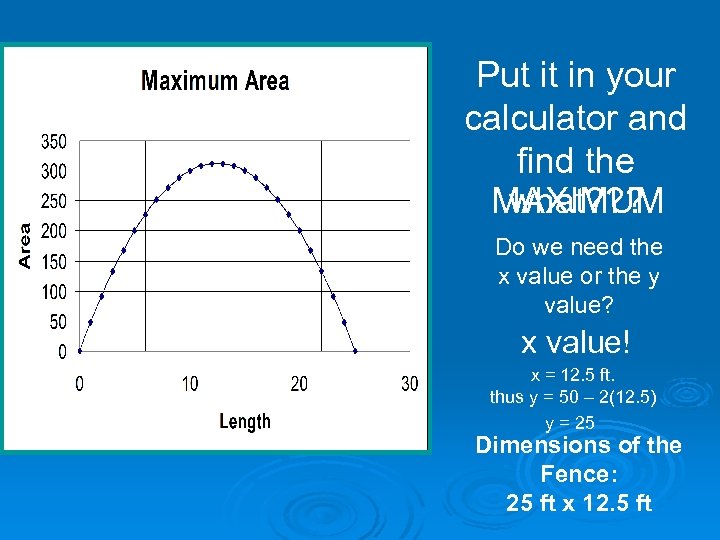Put it in your calculator and find the MAXIMUM what? ? ? Do we need the x value or the y value? x value! x = 12. 5 ft. thus y = 50 – 2(12. 5) y = 25 Dimensions of the Fence: 25 ft x 12. 5 ft

A farmer wants to build two rectangular pens of the same size next to a river so they are separated by one fence. If she has 240 meters of fencing and does not fence the side next to the river, what are the dimensions of the largest area enclosed? What is the largest area?

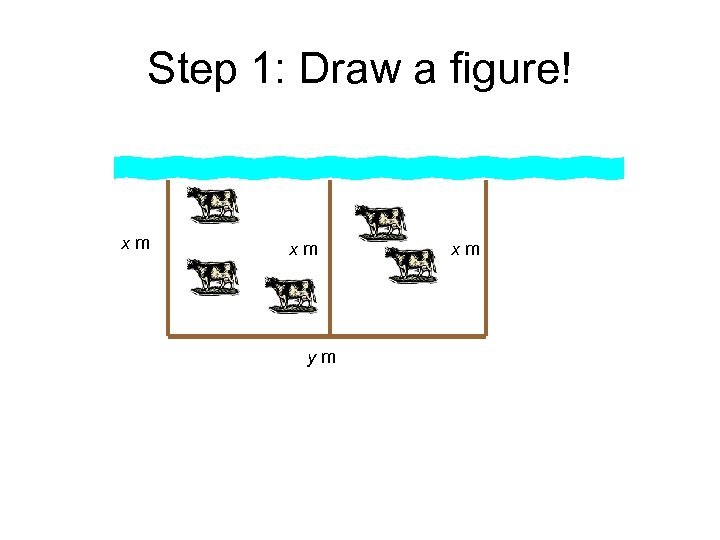Step 1: Draw a figure! xm xm ym xm

Step 2: Set up your equations! Perimeter equation Area equation Solve for y! Substitute y into the area equation Distribute the x. 3 x + y = 240 A = xy y = 240 – 3 x A = x(240 – 3 x) A = 240 x – 3 x 2 Now what type of function do we have? ? So graph it!

Step 3: Graph it! Remember: There are two questions in the problem. 1. What are the dimensions of the largest area enclosed? 2. What is the largest area? So when we graph and find the maximum, are we looking for the x or y for number 1? x! So when we graph and find the maximum, are we looking for the x or y for number 2? y!

The Chesapeake Bay

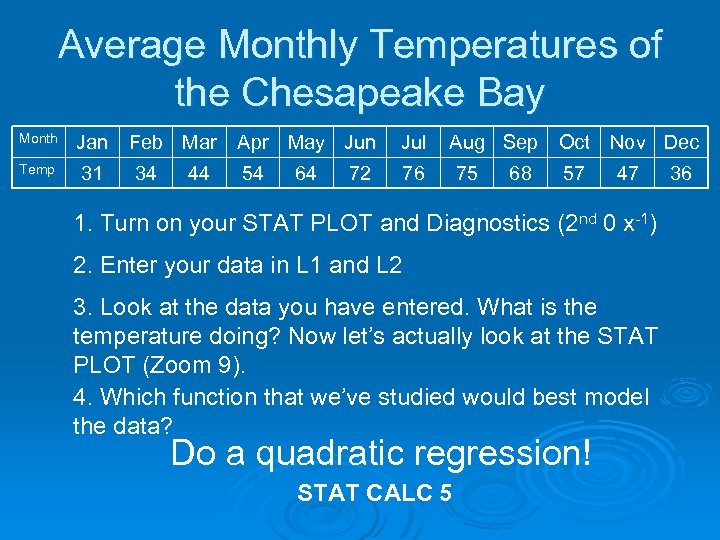Average Monthly Temperatures of the Chesapeake Bay Month Temp Jan Feb Mar Apr May Jun Jul 31 76 34 44 54 64 72 Aug Sep Oct Nov Dec 75 68 57 47 1. Turn on your STAT PLOT and Diagnostics (2 nd 0 x-1) 2. Enter your data in L 1 and L 2 3. Look at the data you have entered. What is the temperature doing? Now let’s actually look at the STAT PLOT (Zoom 9). 4. Which function that we’ve studied would best model the data? Do a quadratic regression! STAT CALC 5 36

What is the r 2 value? r 2 =. 927 This tells us that 92. 7% of the time, the model is a good predictor, and the closer this value is to 1, the closer the data is to the model.

Analysis Ø According to the model, what month does the maximum temperature occur? June! Ø According to the model, during what months would the temperature be 50°? March and October

Darryl is standing on top of the bleachers and throws a football across the field. The data that follows gives the height of the ball in feet versus the seconds since the ball was thrown. Time Ht. 0. 2 0. 6 1 1. 2 1. 5 2 2. 5 2. 8 3. 4 3. 8 4. 5 92 110 134 142 144 140 132 112 90 a. Show a scatter plot of the data. What is the independent variable, and what is the dependent variable? b. What prediction equation (mathematical model) describes this data? c. When will the ball be at a height of 150 feet? d. When will the ball be at a height of 100 feet? e. At what times will the ball be at a height greater than 100 feet? f. When will the ball be at a height of 40 feet? g. When will the ball hit the ground? 44

a. Show a scatter plot of the data. What is the independent variable, and what is the dependent variable? Independent variable (x): Time! (always!) Dependent variable (y): Height

b. What prediction equation (mathematical model) describes this data? QUADRATIC!!

c. When will the ball be at a height of 150 feet? Height (y) l Put 150 in y 2. l What happened? !? Explain.

d. When will the ball be at a height of 100 feet? l Put 100 in y 2 and find the intersection! . 34 seconds and 3. 65 seconds

e. At what times will the ball be at a height greater than 100 feet?

f. When will the ball be at a height of 40 feet? 4. 53 seconds

g. When will the ball hit the ground? Put 0 in y 2 and find the intersection! 4. 98 seconds

Now try it on your own!