Скачать презентацию QTL Mapping Quantitative Trait Loci QTL A Скачать презентацию QTL Mapping Quantitative Trait Loci QTL A

ea7069c1ebd1b7d31db834fc20dc53f4.ppt

  • Количество слайдов: 39

QTL Mapping • Quantitative Trait Loci (QTL): A chromosomal segments that contribute to variation QTL Mapping • Quantitative Trait Loci (QTL): A chromosomal segments that contribute to variation in a quantitative phenotype

Maize Teosinte tb-1/tb-1 mutant maize Maize Teosinte tb-1/tb-1 mutant maize

Mapping Quantitative Trait Loci (QTL) in the F 2 hybrids between maize and teosinte Mapping Quantitative Trait Loci (QTL) in the F 2 hybrids between maize and teosinte

Nature 432, 630 - 635 (02 December 2004) The role of barren stalk 1 Nature 432, 630 - 635 (02 December 2004) The role of barren stalk 1 in the architecture of maize ANDREA GALLAVOTTI(1, 2), QIONG ZHAO(3), JUNKO KYOZUKA(4), ROBERT B. MEELEY(5), MATTHEW K. RITTER 1, *, JOHN F. DOEBLEY(3), M. ENRICO PÈ(2) & ROBERT J. SCHMIDT(1) 1 Section of Cell and Developmental Biology, University of California, San Diego, La Jolla, California 92093 -0116, USA 2 Dipartimento di Scienze Biomolecolari e Biotecnologie, Università degli Studi di Milano, 20133 Milan, Italy 3 Laboratory of Genetics, University of Wisconsin, Madison, Wisconsin 53706, USA 4 Graduate School of Agriculture and Life Science, The University of Tokyo, Tokyo 113 -8657, Japan 5 Crop Genetics Research, Pioneer-A Du. Pont Company, Johnston, Iowa 50131, USA * Present address: Biological Sciences Department, California Polytechnic State University, San Luis Obispo, California 93407, USA

Effects of ba 1 mutations on maize development Mutant Wild type No tassel Tassel Effects of ba 1 mutations on maize development Mutant Wild type No tassel Tassel

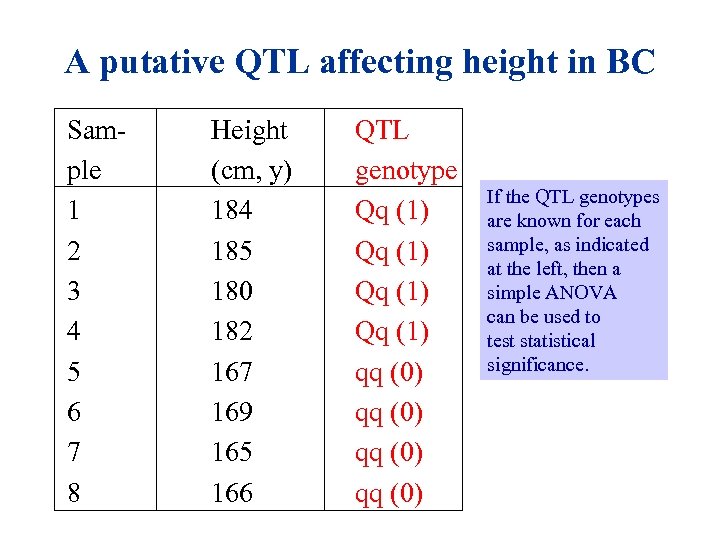A putative QTL affecting height in BC Sam- ple 1 2 3 4 5 A putative QTL affecting height in BC Sam- ple 1 2 3 4 5 6 7 8 Height (cm, y) 184 185 180 182 167 169 165 166 QTL genotype Qq (1) qq (0) If the QTL genotypes are known for each sample, as indicated at the left, then a simple ANOVA can be used to test statistical significance.

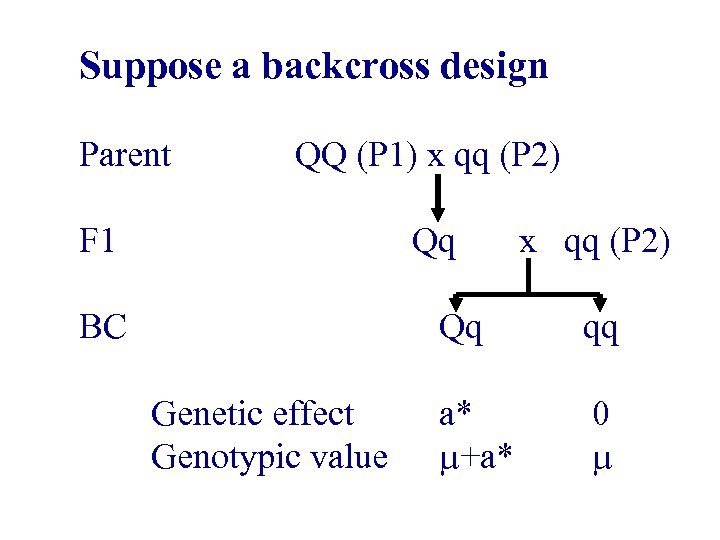Suppose a backcross design Parent F 1 QQ (P 1) x qq (P 2) Suppose a backcross design Parent F 1 QQ (P 1) x qq (P 2) Qq x qq (P 2) BC Genetic effect Genotypic value Qq qq a* +a* 0

QTL regression model The phenotypic value for individual i affected by a QTL can QTL regression model The phenotypic value for individual i affected by a QTL can be expressed as, yi = + a* x*i + ei where is the overall mean, x*i is the indicator variable for QTL genotypes, defined as x*i = 1 for Qq x*i is missing 0 for qq, a* is the “real” effect of the QTL and ei is the residual error, ei ~ N(0, 2).

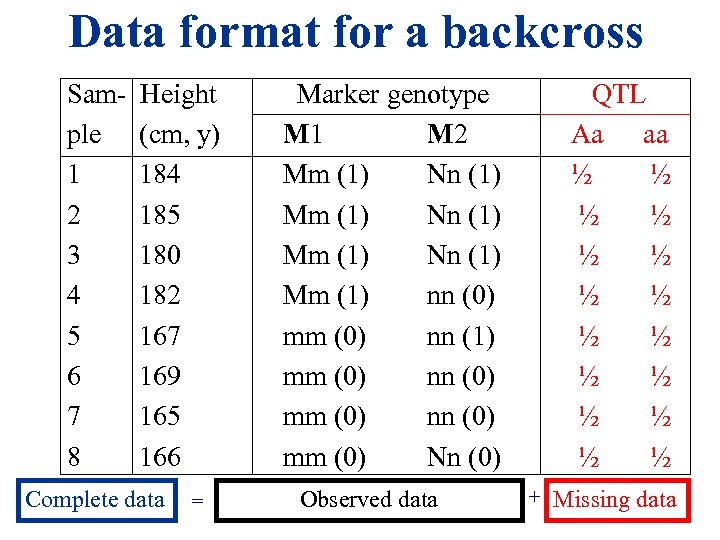Data format for a backcross Sam- Height ple (cm, y) 1 184 2 185 Data format for a backcross Sam- Height ple (cm, y) 1 184 2 185 3 180 4 182 5 167 6 169 7 165 8 166 Complete data = Marker genotype M 1 M 2 Mm (1) Nn (1) Mm (1) nn (0) mm (0) nn (1) mm (0) nn (0) mm (0) Nn (0) Observed data QTL Aa aa ½ ½ ½ ½ + Missing data

Two statistical models I - Marker regression model yi = + axi + ei Two statistical models I - Marker regression model yi = + axi + ei where • xi is the indicator variable for marker genotypes defined as xi = 1 for Mm 0 for mm , • a is the “effect” of the marker (but the marker has no effect. There is the a because of the existence of a putative QTL linked with the marker) • ei ~ N(0, 2)

Heights classified by markers (say marker 1) Marker group Sample size Sample mean Sample Heights classified by markers (say marker 1) Marker group Sample size Sample mean Sample variance Mm mm n 1 = 4 n 0 = 4 m 1=182. 75 m 0=166. 75 s 21= s 20=

The hypothesis for the association between the marker and QTL H 0: m 1 The hypothesis for the association between the marker and QTL H 0: m 1 = m 0 H 1: m 1 m 0 Calculate the test statistic: t = (m 1–m 0)/ [s 2(1/n 1+1/n 0)], where s 2 = [(n 1 -1)s 21+(n 0 -1)s 20]/(n 1+n 0– 2) Compare t with the critical value tdf=n 1+n 2 -2(0. 05) from the t-table. If t > tdf=n 1+n 2 -2(0. 05), we reject H 0 at the significance level 0. 05 there is a QTL If t < tdf=n 1+n 2 -2(0. 05), we accept H 0 at the significance level 0. 05 there is no QTL

Why can the t-test probe a QTL? • • Assume a backcross with two Why can the t-test probe a QTL? • • Assume a backcross with two genes, one marker (alleles M and m) and one QTL (allele Q and q). These two genes are linked with the recombination fraction of r. Frequency Mean effect Mm. Qq (1 -r)/2 m+a Mmqq r/2 m mm. Qq r/2 m+a mmqq (1 -r)/2 m Mean of marker genotype Mm: m 1= (1 -r)/2 (m+a) + r/2 m = m + (1 -r)a Mean of marker genotype mm: m 0= r/2 (m+a) + (1 -r)/2 m = m + ra The difference m 1 – m 0 = m + (1 -r)a – m – ra = (1 -2 r)a

• The difference of marker genotypes can reflect the size of the QTL, • The difference of marker genotypes can reflect the size of the QTL, • This reflection is confounded by the recombination fraction Based on the t-test, we cannot distinguish between the two cases, - Large QTL genetic effect but loose linkage with the marker - Small QTL effect but tight linkage with the marker

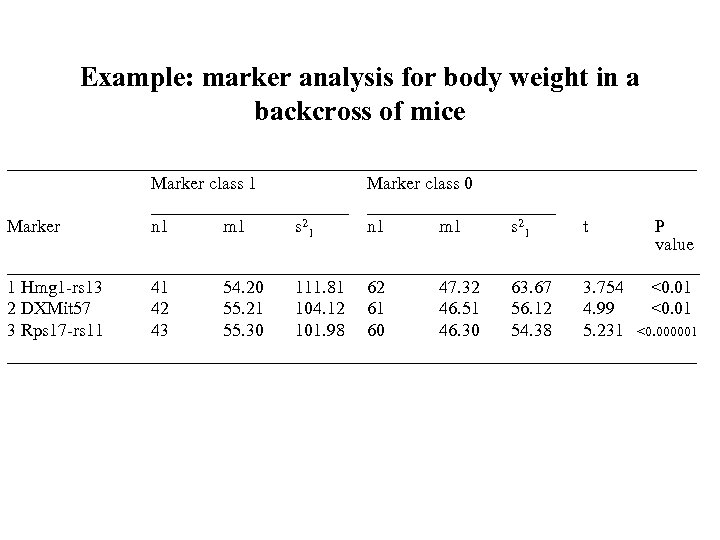Example: marker analysis for body weight in a backcross of mice ___________________________________ Marker class Example: marker analysis for body weight in a backcross of mice ___________________________________ Marker class 1 ___________ n 1 m 1 s 2 1 Marker class 0 ___________ n 1 m 1 s 2 1 t P value _______________________________________ 1 Hmg 1 -rs 13 41 54. 20 111. 81 62 47. 32 63. 67 3. 754 <0. 01 2 DXMit 57 42 55. 21 104. 12 61 46. 51 56. 12 4. 99 <0. 01 3 Rps 17 -rs 11 43 55. 30 101. 98 60 46. 30 54. 38 5. 231 <0. 000001 ___________________________________

Marker analysis for the F 2 In the F 2 there are three marker Marker analysis for the F 2 In the F 2 there are three marker genotypes, MM, Mm and mm, which allow for the test of additive and dominant genetic effects. Genotype MM: Mm: mm: Mean m 2 m 1 m 0 Variance s 22 s 21 s 20

Testing for the additive effect H 0: m 2 = m 0 H 1: Testing for the additive effect H 0: m 2 = m 0 H 1: m 2 m 0 t 1 = (m 2–m 0)/ [s 2(1/n 2+1/n 0)], where s 2 = [(n 2 -1)s 22+(n 0 -1)s 20]/(n 1+n 0– 2) Compare it with tdf=n 2+n 0 -2(0. 05)

Testing for the dominant effect H 0: m 1 = (m 2 + m Testing for the dominant effect H 0: m 1 = (m 2 + m 0)/2 H 1: m 1 (m 2 + m 0)/2 t 2 = [m 1–(m 2 + m 0)/2]/ {[s 2[1/n 1+1/(4 n 2)+1/(4 n 0)]], where s 2 = [(n 2 -1)s 22+(n 1 -1)s 21+(n 0 -1)s 20]/(n 2+n 1+n 0– 3) Compare it with tdf=n 2+n 1+n 0 -3(0. 05)

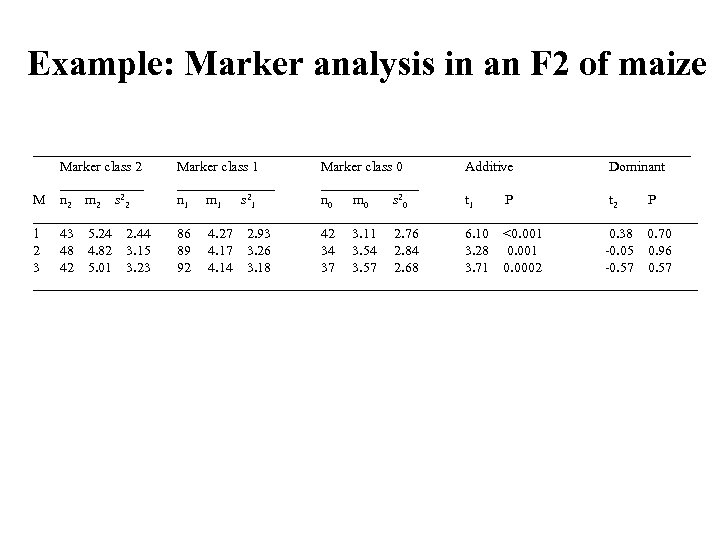Example: Marker analysis in an F 2 of maize _______________________________________________ Marker class 2 Marker Example: Marker analysis in an F 2 of maize _______________________________________________ Marker class 2 Marker class 1 Marker class 0 Additive Dominant ______________ M n 2 m 2 s 22 n 1 m 1 s 21 n 0 m 0 s 20 t 1 P t 2 P ________________________________________________ 1 43 5. 24 2. 44 86 4. 27 2. 93 42 3. 11 2. 76 6. 10 <0. 001 0. 38 0. 70 2 48 4. 82 3. 15 89 4. 17 3. 26 34 3. 54 2. 84 3. 28 0. 001 -0. 05 0. 96 3 42 5. 01 3. 23 92 4. 14 3. 18 37 3. 57 2. 68 3. 71 0. 0002 -0. 57 ________________________________________________

II – QTL regression model based on markers (interval mapping) Suppose gene order Marker II – QTL regression model based on markers (interval mapping) Suppose gene order Marker 1 – QTL – Marker 2 yi = + a*zi + ei where • a* is the “real” effect of a QTL, • zi is an indicator variable describing the probability of individual i to carry the QTL genotype, Qq or qq, given a possible marker genotype, • ei ~ N(0, 2)

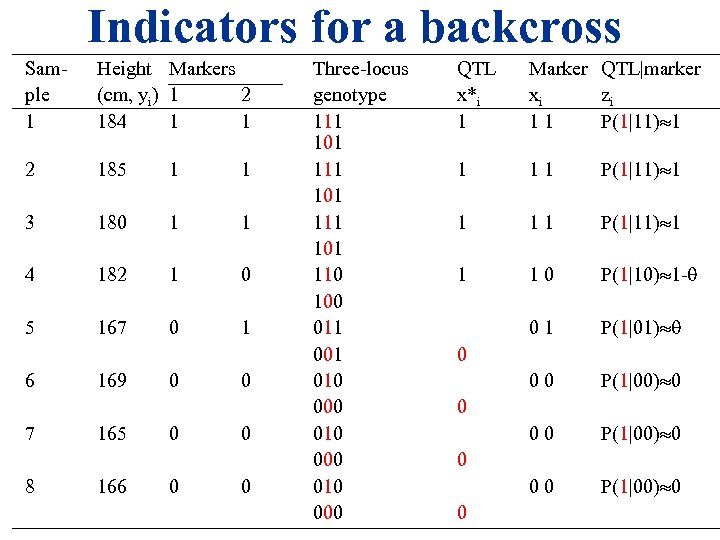Indicators for a backcross Sam- Height Markers ple (cm, yi) 1 2 1 184 Indicators for a backcross Sam- Height Markers ple (cm, yi) 1 2 1 184 1 1 2 185 1 1 3 180 1 1 4 182 1 0 5 167 0 1 6 7 8 169 165 166 0 0 0 Three-locus genotype 111 101 110 100 011 001 010 000 QTL x*i 1 Marker QTL|marker xi zi 1 1 P(1|11) 1 1 1 0 P(1|10) 1 - 0 1 P(1|01) 0 0 P(1|00) 0 0 0

Conditional probabilities ( 1|i or 0|i) of the QTL genotypes (missing) based on marker Conditional probabilities ( 1|i or 0|i) of the QTL genotypes (missing) based on marker genotypes (observed) Marker Genotype 11 10 01 00 QTL genotype Freq. Qq(1) ½(1 -r) (1 -r 1)(1 -r 2)/ (1 -r) 1 ½r (1 -r 1)r 2/r 1 - = 1 -r 1/r ½r r 1(1 -r 2)/r ½(1 -r) r 1 r 2/ (1 -r) 0 Order Marker 1–QTL–Marker 2 qq(0) r 1 r 2/ (1 -r) 0 r 1(1 -r 2)/r = r 1/r (1 -r 1)r 2/r 1 - (1 -r 1)(1 -r 2)/ (1 -r) 1 r is the recombination fraction between two markers r 1 is the recombination fraction between marker 1 and QTL r 2 is the recombination fraction between QTL and marker 2

Interval mapping with regression approach • Consider a marker interval M 1 -M 2. Interval mapping with regression approach • Consider a marker interval M 1 -M 2. We assume that a QTL is located at a particular position between the two markers (r 1 and are fixed) • With response variable, yi, and dependent variable, zi, a regression model is constructed as yi = + a*zi + ei • Statistical software, like SAS, can be used to estimate the parameters ( , a*, 2) for a particular QTL position contained in the regression model • Move the QTL position every 2 c. M from M 1 to M 2 and draw the profile of the F value. The peak of the profile corresponds to the best estimate of the QTL position. F-value M 1 M 2 M 3 M 4 M 5 Testing position

Interval mapping with maximum likelihood • • • Linear regression model for specifying the Interval mapping with maximum likelihood • • • Linear regression model for specifying the effect of a putative QTL on a quantitative trait Mixture model-based likelihood Conditional probabilities of the QTL genotypes (missing) based on marker genotypes (observed) Normal distributions of phenotypic values for each QTL genotype group Log-likelihood equations (via differentiation) EM algorithm Log-likelihood ratios The profile of log-likelihood ratios across a linkage group The determination of thresholds Result interpretations

Linear regression model for specifying the effect of a QTL on a quantitative trait Linear regression model for specifying the effect of a QTL on a quantitative trait yi = + a*zi + ei, i = 1, …, n (latent model) • • • a* is the (additive) effect of the putative QTL on the trait, zi is the indicator variable and defined as 1 when QTL genotype is Qq and 0 when QTL genotype is qq, ei N(0, 2) Observed data: Missing data: Parameters: • yi and marker genotypes M QTL genotypes = ( , a*, 2, =r 1/r) Observed marker genotypes and missing QTL genotypes are connected in terms of the conditional probability ( 1|i or 0|i) of QTL genotypes (Qq or qq), conditional upon marker genotypes (11, 10, 01 or 00).

Mixture model-based likelihood without marker information L(y| ) = i=1 n [½f 1(yi) + Mixture model-based likelihood without marker information L(y| ) = i=1 n [½f 1(yi) + ½f 0(yi)] Sam- ple 1 2 3 4 5 6 7 8 Height (cm, y) 184 185 180 182 167 169 165 166 QTL genotype Qq (1) qq (0)

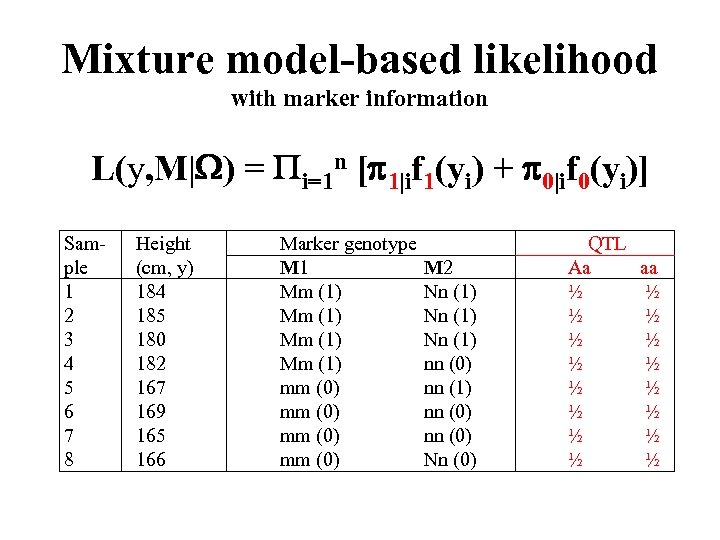Mixture model-based likelihood with marker information L(y, M| ) = i=1 n [ 1|if Mixture model-based likelihood with marker information L(y, M| ) = i=1 n [ 1|if 1(yi) + 0|if 0(yi)] Sam- ple 1 2 3 4 5 6 7 8 Height (cm, y) 184 185 180 182 167 169 165 166 Marker genotype M 1 M 2 Mm (1) Nn (1) Mm (1) nn (0) mm (0) nn (1) mm (0) nn (0) mm (0) Nn (0) QTL Aa ½ ½ ½ ½ aa ½ ½ ½ ½ ½

Conditional probabilities of the QTL genotypes (missing) based on marker genotypes (observed) L(y, M| Conditional probabilities of the QTL genotypes (missing) based on marker genotypes (observed) L(y, M| ) = i=1 n [ 1|if 1(yi) + 0|if 0(yi)] = i=1 n 1 [1 f 1(yi) i=1 n 2 [(1 - ) f 1(yi) i=1 n 3 [ f 1(yi) i=1 n 4 [0 f 1(yi) +0 f 0(yi)] + (1 - ) f 0(yi)] +1 f 0(yi)] Conditional on 11 Conditional on 10 Conditional on 01 Conditional on 00

Normal distributions of phenotypic values for each QTL genotype group f 1(yi) = 1/(2 Normal distributions of phenotypic values for each QTL genotype group f 1(yi) = 1/(2 2)1/2 exp[-(yi- 1)2/(2 2)], 1 = + a* f 0(yi) = 1/(2 2)1/2 exp[-(yi- 0)2/(2 2)], 0 =

Differentiating L with respect to each unknown parameter, setting derivatives equal zero and solving Differentiating L with respect to each unknown parameter, setting derivatives equal zero and solving the log-likelihood equations L(y, M| ) = i=1 n[ 1|if 1(yi) + 0|if 0(yi)] log L(y, M| ) = i=1 n log[ 1|if 1(yi) + 0|if 0(yi)] Define 1|i = 1|if 1(yi)/[ 1|if 1(yi) + 0|if 0(yi)] 0|i = 0|if 1(yi)/[ 1|if 1(yi) + 0|if 0(yi)] (1) (2) 1 = 0 = 2 = = (3) (4) (5) (6)

EM algorithm (1) Give initiate values (0) = ( 1, 0, 2, )(0), (2) EM algorithm (1) Give initiate values (0) = ( 1, 0, 2, )(0), (2) Calculate 1|i(1) and 0|i(1) using Eqs. 1 and 2, (3) Calculate (1) using 1|i(1) and 0|i(1), (4) Repeat (2) and (3) until convergence.

Two approaches for estimating the QTL position ( ) • • View as a Two approaches for estimating the QTL position ( ) • • View as a variable being estimated (derive the log-likelihood equation for the MLE of ), View as a fixed parameter by assuming that the QTL is located at a particular position.

Log-likelihood ratio (LR) test statistics H 0: There is no QTL ( 1= 0 Log-likelihood ratio (LR) test statistics H 0: There is no QTL ( 1= 0 or a* = 0) – reduced model H 1: There is a QTL ( 1 0 or a* 0) – full model Under H 0: L 0 = L(y, M|, a*=0, ) Under H 1: L 1 = L(y, M|^ 1, ^ 0, ^ 2, ) LR = -2(log L 0 – log L 1)

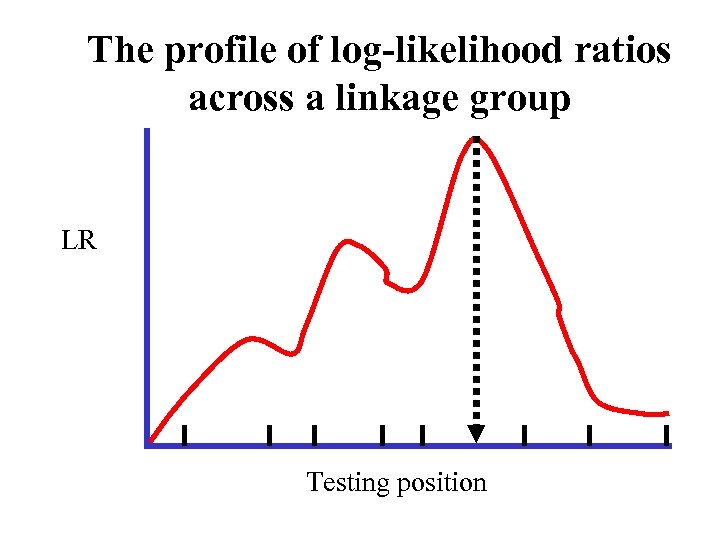The profile of log-likelihood ratios across a linkage group LR Testing position The profile of log-likelihood ratios across a linkage group LR Testing position

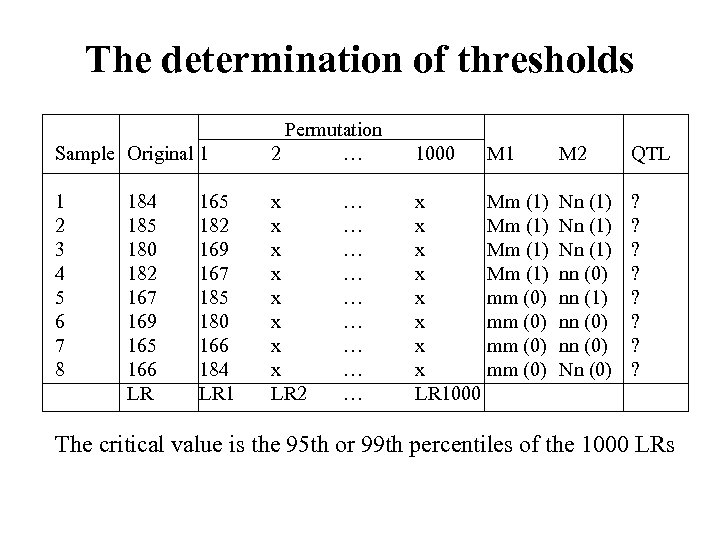The determination of thresholds Permutation Sample Original 1 2 … 1000 M 1 M The determination of thresholds Permutation Sample Original 1 2 … 1000 M 1 M 2 QTL 1 2 3 4 5 6 7 8 x x x x LR 2 … … … … … x x x x LR 1000 Mm (1) mm (0) Nn (1) nn (0) Nn (0) ? ? ? ? 184 185 180 182 167 169 165 166 LR 165 182 169 167 185 180 166 184 LR 1 The critical value is the 95 th or 99 th percentiles of the 1000 LRs

Result interpretations A poplar genome project Objectives: • Identify QTL affecting stemwood growth and Result interpretations A poplar genome project Objectives: • Identify QTL affecting stemwood growth and production using molecular markers; • Develop fast-growing cultivars using marker-assisted selection

Materials and Methods • Poplar hybrids F 1 hybrids from eastern cottonwood (D) euramerican Materials and Methods • Poplar hybrids F 1 hybrids from eastern cottonwood (D) euramerican poplar (E) (a hybrid between eastern cottonwood black poplar) Four hundred fifty (450) F 1 hybrids were planted in a field trial • DNA extraction and marker arrays A total of 560 markers were detected from a subset of F 1 hybrids (90) • Genetic linkage map construction

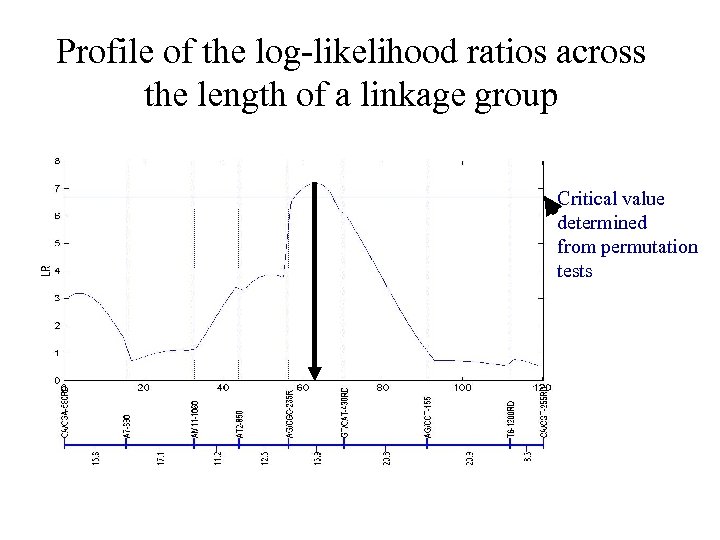Profile of the log-likelihood ratios across the length of a linkage group Critical value Profile of the log-likelihood ratios across the length of a linkage group Critical value determined from permutation tests

Advantages and disadvantages Compared with single marker analysis, interval mapping has several advantages: • Advantages and disadvantages Compared with single marker analysis, interval mapping has several advantages: • The position of the QTL can be inferred by a support interval; • The estimated position and effects of the QTL tend to be asymptotically unbiased if there is only one segregating QTL on a chromosome; • The method requires fewer individuals than single marker analysis for the detection of QTL Disadvantages: • The test is not an interval test (a test that can distinguish whether or not there is a QTL within a defined interval and should be independent of the effects of QTL that are outside a defined region). • Even when there is no QTL within an interval, the likelihood profile on the interval can still exceed the threshold (ghost QTL) if there is QTL at some nearby region on the chromosome. • If there is more than one QTL on a chromosome, the test statistic at the position being tested will be affected by all QTL and the estimated positions and effects of “QTL” identified by this method are likely to be biased. • It is not efficient to use only two markers at a time for testing, since the information from other markers is not utilized.