ed7a3cd1efbe6fbe68f249b0f9ed71ba.ppt
- Количество слайдов: 70

QB or not QB: An Efficient Execution Verification tool for Memory Orderings Ganesh Gopalakrishnan* School of Computing, University of Utah, Salt Lake City, UT Yue Yang* Microsoft Research, Redmond, WA Hemanthkumar Sivaraj* Intel Corporation, Bangalore, India * Work supported in part by SRC Contract 1031. 001 and NSF Award 0219805
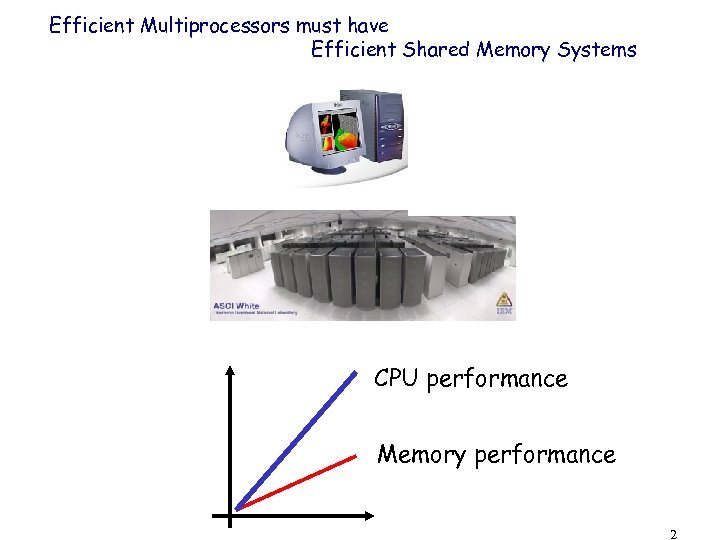
Efficient Multiprocessors must have Efficient Shared Memory Systems CPU performance Memory performance 2
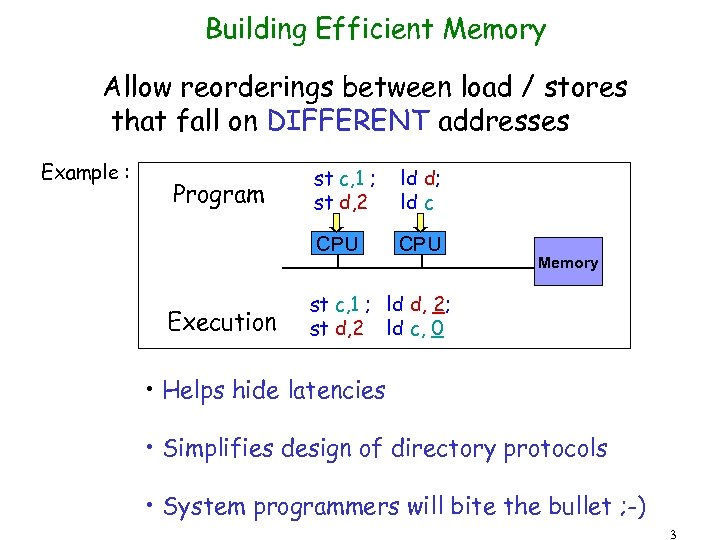
Building Efficient Memory Allow reorderings between load / stores that fall on DIFFERENT addresses Example : Execution ld d; ld c CPU Program st c, 1 ; st d, 2 CPU Memory st c, 1 ; ld d, 2; st d, 2 ld c, 0 • Helps hide latencies • Simplifies design of directory protocols • System programmers will bite the bullet ; -) 3
Permitted reorderings are specified by the shared memory consistency model A VERY complex specification for a real architecture (e. g. Itanium, Power. PC, …) Also of growing concern in Software (e. g. Java Memory Model, Unified Parallel C model, …) 4

MODULAR SPECIFICATION OF MEMORY MODELS legal_itanium exec = (* a given execution *) ? order. require. Linear. Order exec order / require. Write. Operation. Order exec order / require. Program. Order exec order / require. Memory. Data. Dependence exec order / require. Data. Flow. Dependence exec order / require. Coherence exec order / require. Read. Value exec order / require. Atomic. WBRelease exec order / require. Sequential. UC exec order / require. No. UCBypass exec order See IPDPS 2004 5

A MEMORY MODEL RULE IN HOL require. Coherence exec order = !i j. i IN exec / j IN exec ==> is. Wr i / is. Wr j / (i. var = j. var) / order i j / ((attr_of i. var = WB) / (attr_of i. var = UC)) / ((i. wr. Type=Local) / (j. wr. Type=Local) / (i. proc=j. proc) / (i. wr. Type=Remote) / (j. wr. Type=Remote) / (i. wr. Proc=j. wr. Proc)) ==> !p q. p IN exec / q IN exec ==> is. Wr p / is. Wr q / (p. wr. ID = i. wr. ID) / (q. wr. ID = j. wr. ID) / (p. wr. Type = Remote) / (q. wr. Type = Remote) /(p. wr. Proc = q. wr. Proc) ==> order p q 6

How do we know that the actual silicon matches the shared memory model ? ? ! X. X in exec ? Y. Y in exec …. ? ! / … / …. • Pray • Run tests and manually check results • ? What else ? 7

FORMALLY VERIFY “interesting” EXECUTIONS P 1’s exec P 2’s exec st 8 ld 2 … [12 ca 20] = 7 f 869 af 546 f 2 f 14 c r 25 = [45180] <87 b 5 e 547172644 a 8> r 26 = [2 c 2 a 2 c] <44 a 8> r 27 = [45 aa 2 a] <c 58 e> st 8 ld 8 st 2 … [45180] = 87 b 5 e 547172644 a 8 r 25 = [45180] <87 b 5 e 547172644 a 8> [2 c 2 a 2 c] = 44 a 8 [45 aa 2 a] = c 58 e … 8
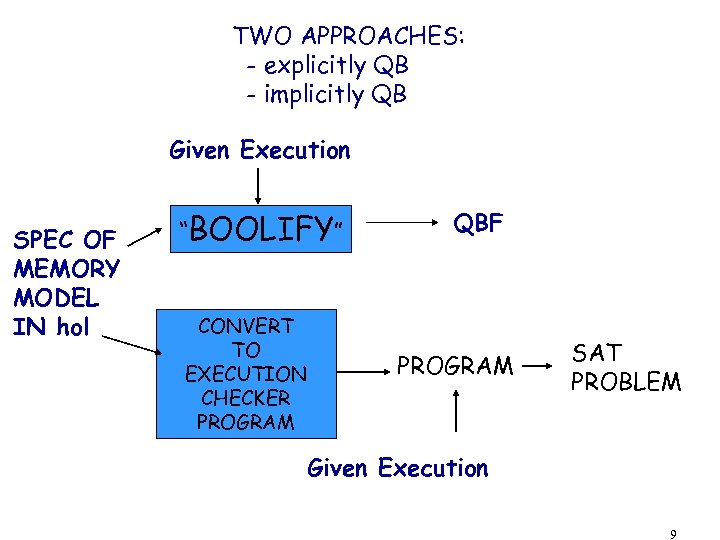
TWO APPROACHES: - explicitly QB - implicitly QB Given Execution SPEC OF MEMORY MODEL IN hol “BOOLIFY” CONVERT TO EXECUTION CHECKER PROGRAM QBF PROGRAM SAT PROBLEM Given Execution 9

AN EXAMPLE require. Mickey. Mouse exec order = !i j. i IN exec / j IN exec ==>( i. op = read / i. data = 35 / j. op = write / j. data = 46 ==> order j i) GIVEN MP EXECUTION… PROCESSOR 1 ------ PROCESSOR 2 ------ read(ADDR, 35) write(ADDR, 46) 10

require. Mickey. Mouse exec order = !i j. i IN exec / j IN exec ==>( i. op = read / i. data = 35 / j. op = write / j. data = 46 ==> order j i) Explicitly QB ! i j : Bool. BOOLIFIED MATRIX Implicitly QB FOR I = 1 to 2 DO / (FOR j = 1 to 2 DO / ( BOOLIFIED MATRIX ) 11

The Intel Itanium® Processor memory model • Has these kinds of instructions : “weak load” or “ordinary load” -- ld “strong load” or “acquire-load” -- ld. acq “weak store” or “ordinary store” -- st “strong store” or “release store” -- st. rel “memory fence” (NOT barrier!) -- mf A few semaphore-types Allows sub-word writes, I/O spaces… We don’t model these details momentarily … 12
![EVEN THIS EXAMPLE HAS A 1 -page “proof” A manual proof… P st [x] EVEN THIS EXAMPLE HAS A 1 -page “proof” A manual proof… P st [x]](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-13.jpg)
EVEN THIS EXAMPLE HAS A 1 -page “proof” A manual proof… P st [x] = 1 mf ld r 1 = [y] <0> Q st. rel [y] = 1 R ld. acq r 2 = [y] <1> Atomicity of st. rel ld r 3 = [x] <0> Load of initial value is before store of every other value 13

CONTRIBUTIONS: Wrote a formal description of Itanium® In Higher Order Logic - modular - extensible - works for many architectures As opposed to relying on concurrent data structures that “pretend to be Itanium®” (the “operational style” ) Showed how, using SAT, executions can be formally verified against the spec 14
![Our Approach Itanium Ordering rules in HOL P st [x] = 1 MP execution Our Approach Itanium Ordering rules in HOL P st [x] = 1 MP execution](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-15.jpg)
Our Approach Itanium Ordering rules in HOL P st [x] = 1 MP execution to be verified Mechanical Program Derivation (to be automated) Checker Program R Q st. rel [y] = 1 ld. acq r 2 = [y] <1> ld mf r 3 = [x] <0> ld r 1 = [y] <0> RECENT WORK • • • Find Offending Clauses Trace their annotations Determine “ordering cycle” Unsat Core Extraction using Zcore Satisfiability Problem with Clauses carrying annotations Sat Solver Unsat Sat Explanation in the form of one possible interleaving 15

Largest example tried to date (courtesy S. Zeisset, Intel) Proc 1 Proc 2 st 8 [12 ca 20] = 7 f 869 af 546 f 2 f 14 c ld r 25 = [45180] <87 b 5 e 547172644 a 8> ld 4 r 24 = [733 a 74] <415 e 304> st 4. rel [175984] = 96 ab 4 e 1 f … 58 more instructions… … 67 more instructions… st 2 [7 c 2 a 00] = 4 bca ld 8 r 87 = [56460] <b 5 c 113 d 7 ce 4783 b 1> • Initially the tool gave a trivial violation • Diagnosed to be forgotten memory initialization • Added method to incorporate memory initialization in our tool • Our tool found the exact same cycle as pointed out by author of test Cycle found thru our tool: st. rel (line 18, P 1) ld (line 22, P 2) mf ld (line 30, P 2) st (line 11, P 1) 16

Statistics Pertaining to Case Study • 140 total instructions • All runs were on a 1. 733 GHz 1 GB Redhat Linux V 9 Athlon • 1 minutes to generate Sat instance • 9 M clauses ( O(n^3) in terms of instructions ) • 117, 823 variables ( not a problem ) • ~1 minute to run Sat (unsat here) – 0. 2 sec to do “real work” • Zcore runs fast – gave 23 clauses in one iteration 17

The rest of the talk • An Intuitive presentation of the Itanium® memory model • Example of how a HOL rule was turned into a SAT generator • How the SAT part was done Throwing an efficient “transitivity blanket” over a problem to cover it with whatever transitivity it begs for !! • What more to expect • Related work 18
![Itanium® memory model thru examples “Ordinary store” … st [x] = 2 … Can Itanium® memory model thru examples “Ordinary store” … st [x] = 2 … Can](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-19.jpg)
Itanium® memory model thru examples “Ordinary store” … st [x] = 2 … Can freely slide in a sequential program… Only rule is coherence The same applies to an “ordinary load” … ld reg 1 = [x] … 19
![Itanium® memory model thru examples “Release store” … st. rel [x] = 2 Things Itanium® memory model thru examples “Release store” … st. rel [x] = 2 Things](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-20.jpg)
Itanium® memory model thru examples “Release store” … st. rel [x] = 2 Things before it in sequential program order can’t happen after it Things after it in sequential program Order may happen before it !! 20
![Itanium® memory model thru examples “Acquire load” … ld. acq r 3 = [y] Itanium® memory model thru examples “Acquire load” … ld. acq r 3 = [y]](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-21.jpg)
Itanium® memory model thru examples “Acquire load” … ld. acq r 3 = [y] Things before it in sequential program order may happen after it Things after it in sequential program Order can’t happen before it !! 21

But with these rules alone, we can’t explain the following legal outcome in Itanium® st. rel [y] = 1 Data dep. ld. acq r 3 = [y] <1> ld reg 1 = [x] <0> ld. acq rule st. rel [x] = 2 ld. acq r 4 = [x] <2> ld reg 2 = [y] <0> Itanium specification DOES NOT try to explain outcomes in terms of “shuffles” of the original instructions! 22

Itanium® rules explain execution outcomes in terms of “progenies” of stores and loads This has turned out to be an unspoken convention in this area for other memory models also… A store generates (n+1) progenies st [y] = 1 Other instructions generate only one ld. acq r 3 = [y] Local copy for P 0 “remote” copy for P 1 23

We wrote such a “breeding assembler” P 1: St a, 1; Ld r 1, a <1>; St b, r 1 <1>; P 2: Ld. acq r 2, b <1>; Ld r 3, a <0>; {id=0; proc=0; pc=0; op= St; var=0; data=1; wr. ID=0; wr. Type=Local; wr. Proc=0; reg=-1; use. Reg=false}; Tuple 1 {id=1; proc=0; pc=0; op= St; var=0; data=1; wr. ID=0; wr. Type=Remote; wr. Proc=0; reg=-1; use. Reg=false}; {id=2; proc=0; pc=0; op= St; var=0; data=1; wr. ID=0; wr. Type=Remote; wr. Proc=1; reg=-1; use. Reg=false}; {id=3; proc=0; pc=1; op= Ld; var=0; data=1; wr. ID=-1; wr. Type=Dont. Care; wr. Proc=-1; reg=0; use. Reg=true}; {id=4; proc=0; pc=2; op= St; var=1; data=1; wr. ID=4; wr. Type=Local; wr. Proc=0; reg=0; use. Reg=true}; . . . {id=5; proc=0; pc=2; op= St; var=1; data=1; wr. ID=4; wr. Type=Remote; wr. Proc=0; reg=0; use. Reg=true}; {id=6; proc=0; pc=2; op= St; var=1; data=1; wr. ID=4; wr. Type=Remote; wr. Proc=1; reg=0; use. Reg=true}; {id=7; proc=1; pc=0; op= Ld. Acq; var=1; data=1; wr. ID=-1; wr. Type=Dont. Care; wr. Proc=-1; reg=1; use. Reg=true}; {id=8; proc=1; pc=1; op= Ld; var=0; data=0; wr. ID=-1; wr. Type=Dont. Care; wr. Proc=-1; reg=2; use. Reg=true} Tuple 9 24
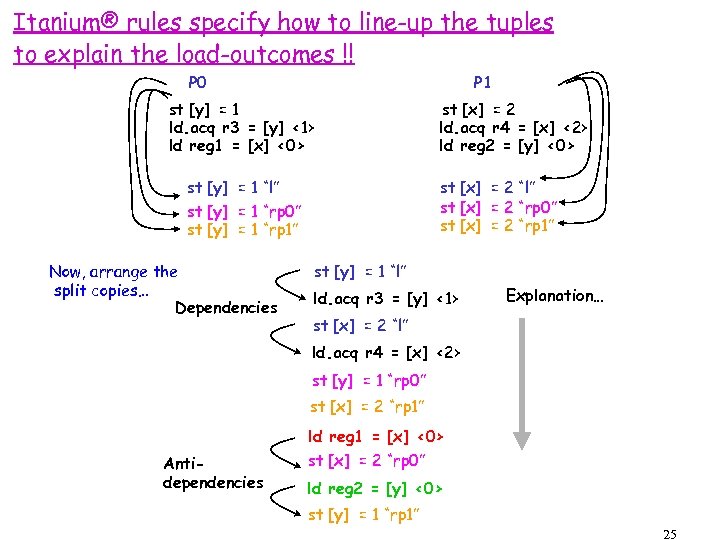
Itanium® rules specify how to line-up the tuples to explain the load-outcomes !! P 0 P 1 st [y] = 1 ld. acq r 3 = [y] <1> ld reg 1 = [x] <0> st [x] = 2 ld. acq r 4 = [x] <2> ld reg 2 = [y] <0> st [y] = 1 “l” st [y] = 1 “rp 0” st [y] = 1 “rp 1” Now, arrange the split copies… Dependencies st [x] = 2 “l” st [x] = 2 “rp 0” st [x] = 2 “rp 1” st [y] = 1 “l” ld. acq r 3 = [y] <1> Explanation… st [x] = 2 “l” ld. acq r 4 = [x] <2> st [y] = 1 “rp 0” st [x] = 2 “rp 1” Antidependencies ld reg 1 = [x] <0> st [x] = 2 “rp 0” ld reg 2 = [y] <0> st [y] = 1 “rp 1” 25
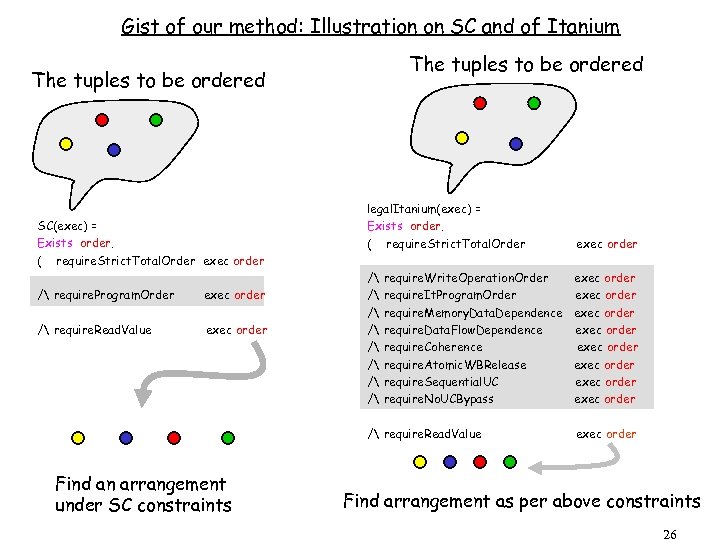
Gist of our method: Illustration on SC and of Itanium The tuples to be ordered SC(exec) = Exists order. ( require. Strict. Total. Order exec order / require. Program. Order exec order / require. Read. Value exec order legal. Itanium(exec) = Exists order. ( require. Strict. Total. Order exec order / / exec order exec order require. Write. Operation. Order require. It. Program. Order require. Memory. Data. Dependence require. Data. Flow. Dependence require. Coherence require. Atomic. WBRelease require. Sequential. UC require. No. UCBypass / require. Read. Value Find an arrangement under SC constraints exec order Find arrangement as per above constraints 26
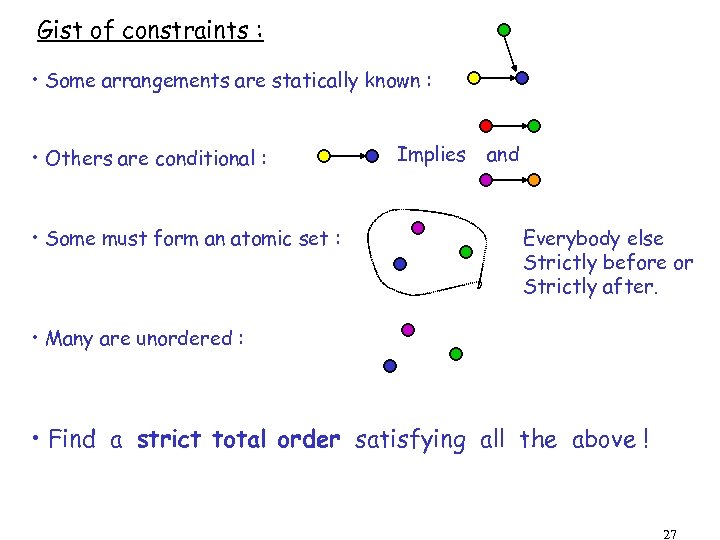
Gist of constraints : • Some arrangements are statically known : • Others are conditional : • Some must form an atomic set : Implies and Everybody else Strictly before or Strictly after. • Many are unordered : • Find a strict total order satisfying all the above ! 27
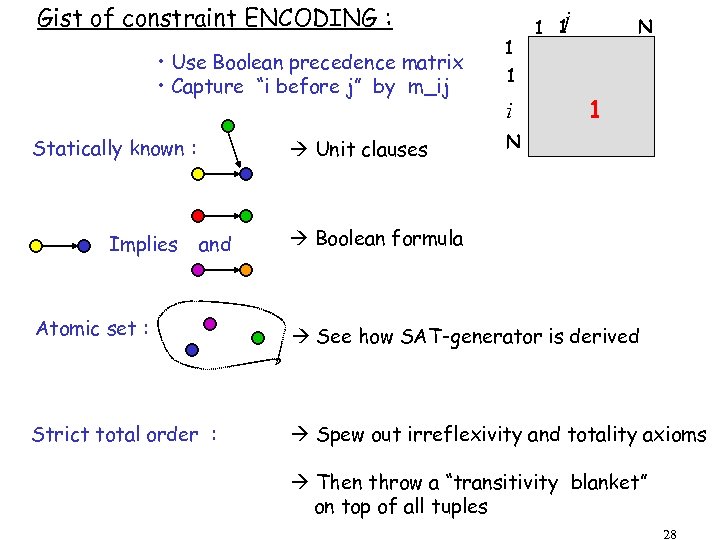
Gist of constraint ENCODING : • Use Boolean precedence matrix • Capture “i before j” by m_ij Statically known : Implies Unit clauses and 1 j 1 1 N 1 i 1 N Boolean formula Atomic set : See how SAT-generator is derived Strict total order : Spew out irreflexivity and totality axioms Then throw a “transitivity blanket” on top of all tuples 28

-Also tried E_ij method - and some incremental SAT (see paper) 29

Approaches to “transitivity blanket” Naïve : For all tuples i, j, and k, generate m_ij / m_jk Too many clauses (1 B for a 1000 -tuple program) Better: Obtain transitive-closure of known orderings and then prune irrelevant parts of the blanket E. g. , if ~m_ij is known, don’t generate m_ij / … … … as well as / m_ij … 30

Obtaining SAT-generator from HOL Initial Spec atomic. WBRelease(exec, order) = forall (i in exec). (j in exec). (k in exec). (i. op = St. Rel) / (i. wr. Type = Remote) / (attr_of i. var = WB) / (i. wr. ID = k. wr. ID) / order(i, j) / order(j, k) ==> (j. wr. ID = i. wr. ID) Applying Contrapositive atomic. WBRelease(exec, order) = forall (i in exec). (j in exec). (k in exec). (i. op = St. Rel) / (i. wr. Type = Remote) / (attr_of i. var = WB) / (i. wr. ID = k. wr. ID) / ~(j. wr. ID = i. wr. ID) ==> ~(order(i, j) / order(j, k)) After Reducing quantifier Scopes atomic. WBRelease(exec, order) = forall (i in exec). (i. op = St. Rel) / (i. wr. Type = Remote) / (attr_of i. var = WB) ==> forall (k in exec). (i. wr. ID = k. wr. ID) ==> forall (j in exec). ~(j. wr. ID = i. wr. ID) ==> ~(order(i, j) / order(j, k)) 31

…Obtaining SAT-generator from HOL Transformed Spec atomic. WBRelease(exec, order) = forall (i in exec). (i. op = St. Rel) / (i. wr. Type = Remote) / (attr_of i. var = WB) ==> forall (k in exec). (i. wr. ID = k. wr. ID) ==> forall (j in exec). ~(j. wr. ID = i. wr. ID) ==> ~(order(i, j) / order(j, k)) Functional Program that generates the constraints (will be automated) atomic. WBRelease(exec) = forall(i, exec, wb(i)) wb(i) = if ~((attr_of i. var=WB) & (i. op=St. Rel) & (i. wr. Type=Remote) then true else forall(k, exec, wb 1(i, k)) wb 1(i, k) = if ~(i. wr. ID=k. wr. ID) else forall(j, exec, wb 2(i, k, j)) then true wb 2(i, k, j) = if (j. wr. ID=i. wr. ID) else ~(order(i, j) & order(j, k)) then true forall(i, S, e(i)) = for all i in S : e(i) (* foldr( map (fn i -> e(i)) (S) (&), true) *) 32
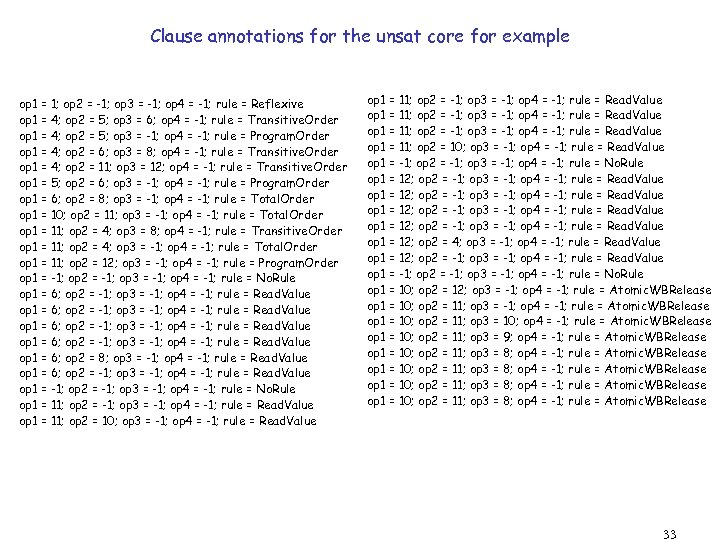
Clause annotations for the unsat core for example op 1 = 1; op 2 = -1; op 3 = -1; op 4 = -1; rule = Reflexive op 1 = 4; op 2 = 5; op 3 = 6; op 4 = -1; rule = Transitive. Order op 1 = 4; op 2 = 5; op 3 = -1; op 4 = -1; rule = Program. Order op 1 = 4; op 2 = 6; op 3 = 8; op 4 = -1; rule = Transitive. Order op 1 = 4; op 2 = 11; op 3 = 12; op 4 = -1; rule = Transitive. Order op 1 = 5; op 2 = 6; op 3 = -1; op 4 = -1; rule = Program. Order op 1 = 6; op 2 = 8; op 3 = -1; op 4 = -1; rule = Total. Order op 1 = 10; op 2 = 11; op 3 = -1; op 4 = -1; rule = Total. Order op 1 = 11; op 2 = 4; op 3 = 8; op 4 = -1; rule = Transitive. Order op 1 = 11; op 2 = 4; op 3 = -1; op 4 = -1; rule = Total. Order op 1 = 11; op 2 = 12; op 3 = -1; op 4 = -1; rule = Program. Order op 1 = -1; op 2 = -1; op 3 = -1; op 4 = -1; rule = No. Rule op 1 = 6; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 6; op 2 = 8; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 6; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = -1; op 2 = -1; op 3 = -1; op 4 = -1; rule = No. Rule op 1 = 11; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 11; op 2 = 10; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = -1; op 2 = -1; op 3 = -1; op 4 = -1; rule = No. Rule op 1 = 12; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 12; op 2 = 4; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 12; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = -1; op 2 = -1; op 3 = -1; op 4 = -1; rule = No. Rule op 1 = 10; op 2 = 12; op 3 = -1; op 4 = -1; rule = Atomic. WBRelease op 1 = 10; op 2 = 11; op 3 = 10; op 4 = -1; rule = Atomic. WBRelease op 1 = 10; op 2 = 11; op 3 = 9; op 4 = -1; rule = Atomic. WBRelease op 1 = 10; op 2 = 11; op 3 = 8; op 4 = -1; rule = Atomic. WBRelease 33
![1 2 3 4 denotes an op st [x] = 1 mf 5 ld 1 2 3 4 denotes an op st [x] = 1 mf 5 ld](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-34.jpg)
1 2 3 4 denotes an op st [x] = 1 mf 5 ld r 1 = [y] <0> 6 7 8 Denotes op numbers. Store has both local and remote exec 9 10 st. rel [y] = 1 ld. acq r 2 = [y] <1> 11 ld 12 r 3 = [x] <0> 34
![1 2 3 4 st [x] = 1 mf 5 ld r 1 = 1 2 3 4 st [x] = 1 mf 5 ld r 1 =](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-35.jpg)
1 2 3 4 st [x] = 1 mf 5 ld r 1 = [y] <0> op 1 = 4; op 2 = 5; op 3 = -1; op 4 = -1; rule = Program. Order 6 7 8 9 10 st. rel [y] = 1 ld. acq r 2 = [y] <1> 11 ld 12 r 3 = [x] <0> 35
![1 2 3 4 st [x] = 1 mf 5 ld r 1 = 1 2 3 4 st [x] = 1 mf 5 ld r 1 =](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-36.jpg)
1 2 3 4 st [x] = 1 mf 5 ld r 1 = [y] <0> 6 7 8 op 1 = 5; op 2 = 6; op 3 = -1; op 4 = -1; rule = Program. Order 9 10 st. rel [y] = 1 ld. acq r 2 = [y] <1> 11 ld 12 r 3 = [x] <0> 36
![1 2 3 4 st [x] = 1 op 1 = 6; op 2 1 2 3 4 st [x] = 1 op 1 = 6; op 2](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-37.jpg)
1 2 3 4 st [x] = 1 op 1 = 6; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value mf 5 ld r 1 = [y] <0> 6 7 8 9 10 st. rel [y] = 1 ld. acq r 2 = [y] <1> 11 ld 12 r 3 = [x] <0> op 1 = 6; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 6; op 2 = 8; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 6; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value 37
![1 2 3 4 st [x] = 1 mf 5 6 ld r 1 1 2 3 4 st [x] = 1 mf 5 6 ld r 1](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-38.jpg)
1 2 3 4 st [x] = 1 mf 5 6 ld r 1 = [y] <0> 7 8 9 10 st. rel [y] = 1 ld. acq r 2 = [y] <1> ld r 3 = [x] <0> 11 12 op 1 = 10; op 2 = 12; op 3 = -1; op 4 = -1; rule = Atomic. WBRelease op 1 = 10; op 2 = 11; op 3 = 10; op 4 = -1; rule = Atomic. WBRelease op 1 = 10; op 2 = 11; op 3 = 9; op 4 = -1; rule = Atomic. WBRelease op 1 = 10; op 2 = 11; op 3 = 8; op 4 = -1; rule = Atomic. WBRelease 38
![1 2 3 4 st [x] = 1 mf 5 ld r 1 = 1 2 3 4 st [x] = 1 mf 5 ld r 1 =](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-39.jpg)
1 2 3 4 st [x] = 1 mf 5 ld r 1 = [y] <0> 6 7 8 9 10 st. rel [y] = 1 ld. acq r 2 = [y] <1> 11 ld op 1 = 11; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 11; op 2 = 10; op 3 = -1; op 4 = -1; rule = Read. Value 12 r 3 = [x] <0> 39
![1 2 3 4 st [x] = 1 mf 5 6 ld r 1 1 2 3 4 st [x] = 1 mf 5 6 ld r 1](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-40.jpg)
1 2 3 4 st [x] = 1 mf 5 6 ld r 1 = [y] <0> 7 8 op 1 = 11; op 2 = 12; op 3 = -1; op 4 = -1; rule = Program. Order 9 10 st. rel [y] = 1 ld. acq r 2 = [y] <1> 11 ld 12 r 3 = [x] <0> 40
![1 2 3 4 st [x] = 1 mf 5 ld r 1 = 1 2 3 4 st [x] = 1 mf 5 ld r 1 =](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-41.jpg)
1 2 3 4 st [x] = 1 mf 5 ld r 1 = [y] <0> 6 7 8 9 10 st. rel [y] = 1 ld. acq r 2 = [y] <1> 11 ld op 1 = 12; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 12; op 2 = 4; op 3 = -1; op 4 = -1; rule = Read. Value op 1 = 12; op 2 = -1; op 3 = -1; op 4 = -1; rule = Read. Value 12 r 3 = [x] <0> 41

CONCLUSIONS • An execution verification method for real memory models • Convert HOL spec of memory model to SAT-generator • Given an execution, run SAT-generator, and generate a SAT-instance • Unsat core gives violating cycle • Works for a few hundred total assembly language instructions 42

What to expect • There is only so much engineering one can put-in before making the checker code suspect • About 500 total instructions may be checkable • To scale beyond this size, we may need to sacrifice completeness (e. g. limited transitivity instantiation good for bug-hunting) • Incremental SAT methods can definitely pay-off • Worst-case (for exhaustive checking) is still bad 43

Related Work • Yuan Yu encoded Alpha axioms in FOL and solved using Simplify • TSOtool (ISCA’ 04, Hangal et. al. ) - TSO much simpler than Itanium - They deliberately omit ordering rules to keep their checker polynomial (e. g. “ordering unrelated stores”) - Hence incomplete - Very long executions checked - Most industrial in-house checkers are similar 44

Extra Slides 45
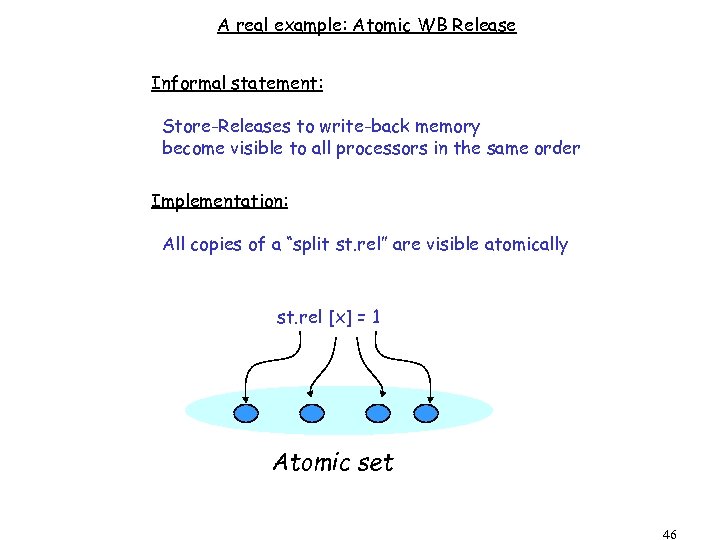
A real example: Atomic WB Release Informal statement: Store-Releases to write-back memory become visible to all processors in the same order Implementation: All copies of a “split st. rel” are visible atomically st. rel [x] = 1 Atomic set 46
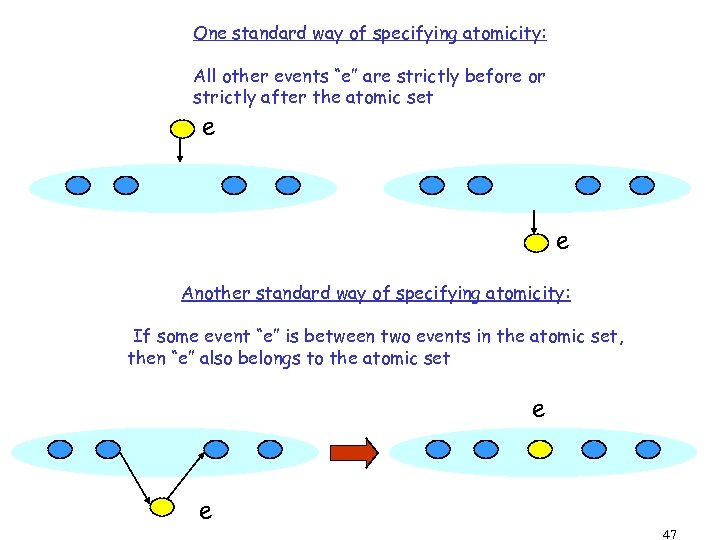
One standard way of specifying atomicity: All other events “e” are strictly before or strictly after the atomic set e e Another standard way of specifying atomicity: If some event “e” is between two events in the atomic set, then “e” also belongs to the atomic set e e 47

Constraint (Sat) Encoding Approach #1 n logn approach (“small domain” encoding) • Attach a word w_t of 2 bits to each tuple t • Tuple i before Tuple j --> Assert wi < wj • Strict. Total. Order --> Assert that the wt words are distinct • Smaller # of Boolean Vars • Much Harder SAT instances (abandoned for now) Illustration on 4 tuples x 00 x 01 x 10 x 11 x 20 x 21 x 30 x 31 require. Strict. Total. Order order exec require. Other. Order order require. Read. Value order exec For all i, j: xi 1, xi 0 != xj 1, xj 0 A system of constraints with primitive constraint xi 1, xi 0 < xj 1, xj 0 48

Constraint Encoding Approach #2 n n approach (“e_ij” encoding) • Assign a matrix position mij for each pair of tuples ti and tj • Tuple i before Tuple j --> Assert mij true • Strict. Total. Order --> Assert Irreflexitivity, Transitivity, Totality • Larger # of Boolean Vars • Easier SAT instances (being pursued now) Illustration on 4 tuples . j. . . i. mij. . . Forall i : ~mii. . require. Strict. Total. Order order exec require. Other. Order order require. Read. Value order exec Forall i, j : mij / mji Forall i, j, k : mij / mjk => mik A system of constraints with primitive constraint mij 49
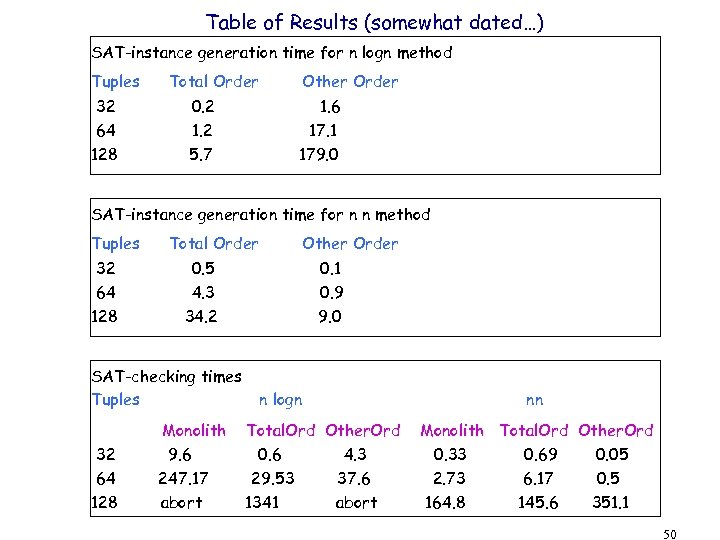
Table of Results (somewhat dated…) SAT-instance generation time for n logn method Tuples Total Order Other Order 32 64 0. 2 1. 6 17. 1 128 5. 7 179. 0 SAT-instance generation time for n n method Tuples 32 64 128 Total Order 0. 5 4. 3 34. 2 SAT-checking times Tuples 32 64 128 Other Order Monolith 9. 6 247. 17 abort 0. 1 0. 9 9. 0 n logn Total. Ord Other. Ord 0. 6 4. 3 29. 53 37. 6 1341 abort nn Monolith Total. Ord Other. Ord 0. 33 0. 69 0. 05 2. 73 6. 17 0. 5 164. 8 145. 6 351. 1 50
![Example execution (Table 18, pg. 31 of App note) P st [x] = 1 Example execution (Table 18, pg. 31 of App note) P st [x] = 1](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-51.jpg)
Example execution (Table 18, pg. 31 of App note) P st [x] = 1 mf Q st. rel [y] = 1 R ld. acq r 2 = [y] <1> ld r 3 = [x] <0> ld r 1 = [y] <0> • The Sat instance generated for the above example is UNSAT. • Next few slides show automated approach to detect the root cause cycle. • We will ignore the reflexive and transitive rules in these slides (they are necessary to force unsat, but useless in building a cycle!!) 51

Good Case-study Illustrating Program Derivation from Formal Specs • Initial specs: HOL • Formal derivation of tail-recursive functional programs • “Code generation” consists of generating Boolean clauses • Source-level optimizations • The use of incremental SAT can perhaps be directed by “functional scripts” that are automatically generated • Use of Unsat cores to pinpoint errors – Choose Boolean encoding method – Re-target code generation correspondingly – Record known orderings (e. g. , “i before j”) – these manifest as unit clauses – Infer others (e. g. , “not j before i”) - generate unit-clauses for these too – Prevent generating transitivity axioms that depend on “j before i” 52

Concluding Remarks • Main source of complexity: the transitivity axiom • “Lazy” methods for handling transitivity must be investigated • Hybrid Sat encoding (partly nn and partly n log n) can also help as was the experience of Lahiri, Seshia, and Bryant • Analyzing larger programs: – Somehow view program in terms of “basic blocks” – Treat each basic block as super instruction – If super-instruction unordered, no need to descend into basic block • Exploit incremental Sat when same litmus tests are rerun • Try modeling another weak memory model 53

Extra Slides 54

Unsat Core generation • The CNF file generated by the sat-generating program is solved using zchaff. • If SAT, then we get a satisfying assignment. • First n*n variables in the assignment correspond to the n*n variables in our ordering. Can be used to output a valid ordering of the exec. • If UNSAT, then need a way to find a “root-cause” for the illegality of the execution. • We use unsatisfiable core generation to get to the root cause. • An unsatisfiable core of an unsatisfiable Sat instance is a subset of clauses of the formula such that its conjunction is still UNSAT. 55

Generating Unsatisfiable Core • Zchaff can be told to generate resolution trace while checking for Sat. • Zcore – tool that takes as input a CNF file and resolution trace produced by zchaff and produces unsatisfiable core. • Zcore available as part of zchaff. • Unsatisfiable core is another CNF file with the reduced set of clauses. • Can be fed back into zchaff/zcore to generate a potentially smaller unsatisfiable core. • Process repeated till fixed point reached. 56

Mapping back to root-cause • Clauses in the unsatisfiable core contain the ordering violation information in them • Tool to home in towards the root-cause for the violation • If the root cause is not something trivial, then the cause is usually a cycle of instructions. Each link in the cycle corresponds to an ordering requirement between the instuctions involved. • If cycle exists, then Transitivity can be applied to show that Irreflexivity is not satisfied. • Input to the tool to generate root cause: – The original set of annotated machine instructions for all processors – The default values stored in memory locations at the beginning of the execution – Clause annotations for the clauses that form the unsatisfiable core 57

Root-cause cycle analysis algorithm Each Read. Value rule generates a set of clauses. From the annotations, find the tuples that come from the same Read. Value rule (two different exec will be involved in a rule) – Extract the exec out of the annotations and get the corresponding instructions (using the proc and pc values) From the data being used in the ld instruction and the default date value for the corresponding memory address, it can be seen if the effect of a store is being reflected in a load. This way the dependency between a load and a store is established. The above is done for all the Read. Value rules in the annotations exec (and the corresponding instructions) on both sides of a mf that form a link in the cycle are inferred based on Program. Order rule annotations and the pc values involved. The other missing links in the violating cycle are also inferred based on the remaining Program. Order rule annotations. 58

A taxonomy of Formal methods to specify industrial Relaxed Memory Models • Operational – Operational models of industrial memory models are complex – Running them inside a standard model-checker is too slow! – Utility for verification is limited – Provides limited insight • Axiomatic – Much more precise – Orderings must ideally be expressed thru an ORTHOGONAL set of rules – No such prior axiomatic specs of industrial memory models 59
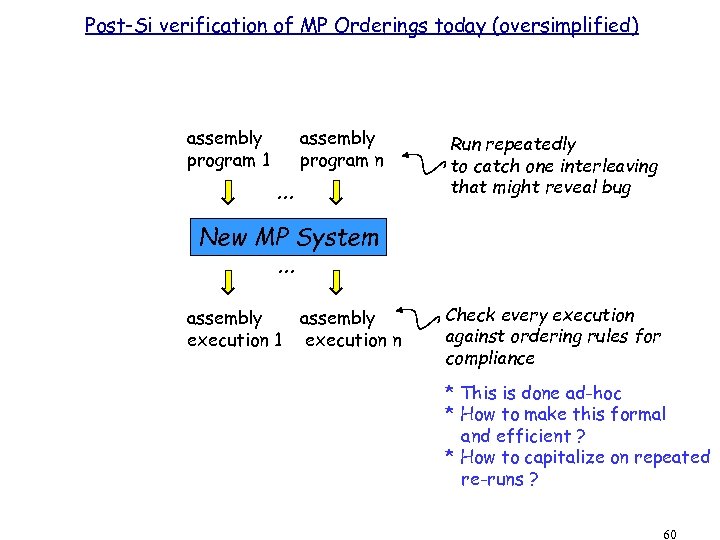
Post-Si verification of MP Orderings today (oversimplified) assembly program 1 assembly program n . . . Run repeatedly to catch one interleaving that might reveal bug New MP System. . . assembly execution 1 assembly execution n Check every execution against ordering rules for compliance * This is done ad-hoc * How to make this formal and efficient ? * How to capitalize on repeated re-runs ? 60

Explanation of Illegal Executions (p 31 of Itanium App Note – search 251429) P us: st [x] = 1 Q sr: st. rel [y] = 1 mf: mf R la: ld. acq r 2 = [y] <1> ul 2: ld r 3 = [x] <0> ul 1: ld r 1 = [y] <0> • US >> MF ; hence RVr(US) F(MF) • MF >> UL 1 ; hence F(MF) R(UL 1) • …many reasons… hence R(UL 1) RVp(SR) • If RVr(SR) R(UL 1) and RVr(SR) UL 1 RVp(SR) , WB release atomicity of SR is violated, thus R(UL 1) RVr(SR) • …five lines of reasons Hence RVr(SR) R(LA) • Since LA >> UL 2, R(LA) R(UL 2) • Another para of reasons LV(Sr 2) R(UL 2) LV(SR 1) RVp(SR 1) RVq(SR 1) F(MF 1) R(UL 1) RVq(SR 2) RVp(SR 2). But can’t allow due to atomicity of SR. 61
![Checking Executions and Providing Explanations (present approach) P st [x] = 1 mf Q Checking Executions and Providing Explanations (present approach) P st [x] = 1 mf Q](https://present5.com/presentation/ed7a3cd1efbe6fbe68f249b0f9ed71ba/image-62.jpg)
Checking Executions and Providing Explanations (present approach) P st [x] = 1 mf Q st. rel [y] = 1 R ld. acq r 2 = [y] <1> ld r 3 = [x] <0> ld r 1 = [y] <0> • Published approaches are very labor-intensive paper-and-pencil proofs • Clearly this can’t scale (6 instruction MP program takes 1 -page of detailed mathematical proof • What about the combinatorics of reasoning about 200 instructions? • Approaches actually used within the industry involves the use of “checkers” • Details of these checkers are unknown (How complete? How scalable? ) 62

The rest of the talk • Itanium memory model in Higher Order Logic • Our HOL specs translation “sat-generating checker programs” • Execution to be checked translation by above program to Sat • Each assembly instruction clauses it generates + annotations • When Sat, what interleaving explains? • When Unsat, how to get “core” (root-cause) + annotations on core • Translating annotations on core to cycle on original program (well, not so high actually… ) 63

• Itanium memory model in Higher Order Logic (well, not so high actually… ) The initial focus of our presentation : - How to model an execution ? - Why use “split stores” in modeling ? 64

But, how do we check executions against such specs? SC(exec) = Exists order. ( require. Strict. Total. Order exec order legal. Itanium(exec) = Exists order. ( require. Strict. Total. Order exec order / require. Program. Order exec order / require. Read. Value exec order / / exec order exec order require. Write. Operation. Order require. It. Program. Order require. Memory. Data. Dependence require. Data. Flow. Dependence require. Coherence require. Atomic. WBRelease require. Sequential. UC require. No. UCBypass / require. Read. Value Execution 1 st c, 1 ; ld d, 2; st d, 2 ld c, 0 exec order Execution 2 st c, 1 ; ld d, 2; st d, 2 ld c, 1 e. g. , which execution is legal under which memory model ? 65

• Itanium memory model in Higher Order Logic • Our HOL specs translation “sat-generating checker programs” (well, not so high actually… ) 66

• Itanium memory model in Higher Order Logic • Our HOL specs translation “sat-generating checker programs” • Execution to be checked translation by above program to Sat (well, not so high actually… ) 67
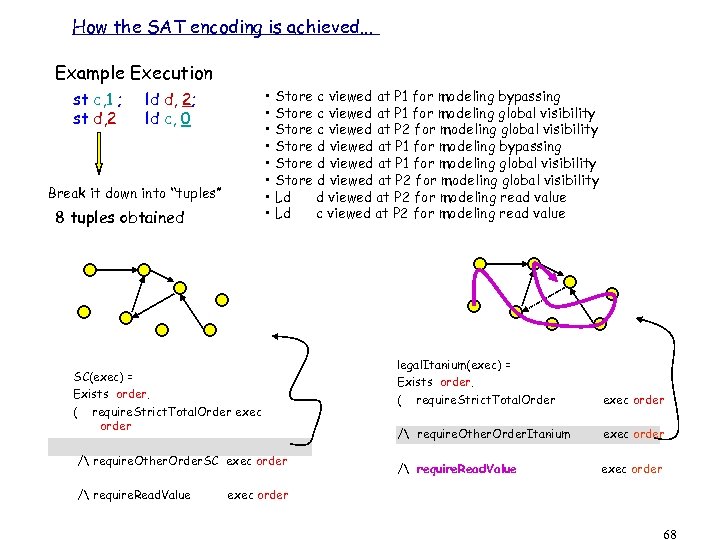
How the SAT encoding is achieved. . . Example Execution st c, 1 ; st d, 2 • Store c viewed at P 1 for modeling bypassing • Store c viewed at P 1 for modeling global visibility • Store c viewed at P 2 for modeling global visibility • Store d viewed at P 1 for modeling bypassing • Store d viewed at P 1 for modeling global visibility • Store d viewed at P 2 for modeling global visibility • Ld d viewed at P 2 for modeling read value • Ld c viewed at P 2 for modeling read value ld d, 2; ld c, 0 Break it down into “tuples” 8 tuples obtained SC(exec) = Exists order. ( require. Strict. Total. Order exec order / require. Other. Order. SC exec order / require. Read. Value legal. Itanium(exec) = Exists order. ( require. Strict. Total. Order exec order / require. Other. Order. Itanium exec order / require. Read. Value exec order 68

Explaining the results of Sat • Itanium memory model in Higher Order Logic • Our HOL specs translation “sat-generating checker programs” • Execution to be checked translation by above program to Sat • Each assembly instruction clauses it generates + annotations • When Sat, what interleaving explains? • When Unsat, how to get “core” (root-cause) + annotations on core • Translating annotations on core to cycle on original program (well, not so high actually… ) 69

Clause Annotations • Each clause generated by the sat-generating checker program also generates an associated tuple. • This tuple has information pertaining to the clause’s source. • Each tuple has the following information – The exec involved in generating the clause (upto a maximum of 4 exec could generate a clause) – The proc value of the processor whose instructions were used to generate this clause (taken from the tuples generated by the gentuple program) – The pc value of the instruction that was the source for this tuple – The name of the memory ordering rule the application of which generated this tuple (Read. Value, Program. Order, Reflexive, etc) • The clause annotation looks as follows < proc, pc, op 1, op 2, op 3, op 4, Rule. Name > 70
ed7a3cd1efbe6fbe68f249b0f9ed71ba.ppt