Q Левая часть Правая часть Левая часть М

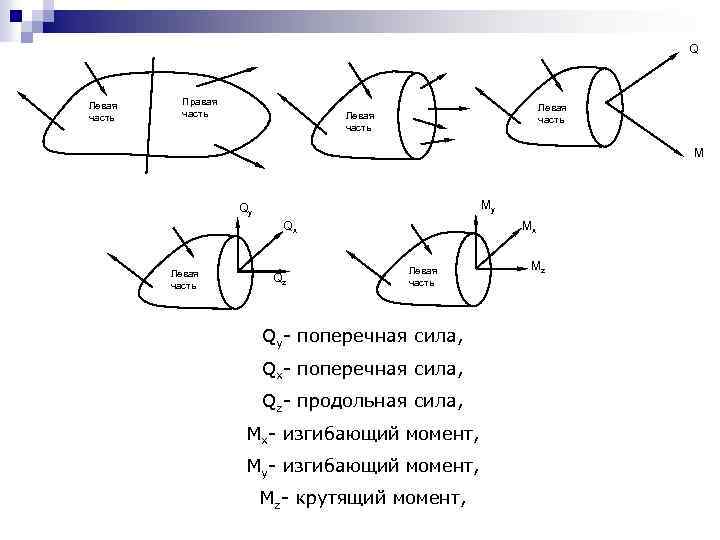Q Левая часть Правая часть Левая часть М Му Qу Qх Левая часть Qz Мх Левая часть Qy- поперечная сила, Qх- поперечная сила, Qz- продольная сила, Мх- изгибающий момент, Му- изгибающий момент, Мz- крутящий момент, Мz

Х=0 Р 1 х + Р 2 х + …+ Qх = 0 Qх = - (Р 1 х + Р 2 х + …) Qу = - (Р 1 у Qz = - (Р 1 z Mх = - (Mхp 1 Mу = - (Mуp 1 Mz = - (Mzp 1 + + + Р 2 у + …) Р 2 z + …) Mхp 2 + …) Mуp 2 + …) Mzp 2 + …) Т. е. внутренняя сила или момент равны суммарной внешней нагрузке приложенной слева от рассматриваемого сечения и взятой с противоположенным знаком.

Существует три основных вида нагружения: - Растяжение – силы направлены только вдоль оси стержня (возникает только продольная сила). - Кручение – силы действуют в плоскости перпендикулярной оси стержня, но их линии действия не проходят через ось сечения (возникает только крутящий момент). - Изгиб – силы действуют в плоскости перпендикулярной оси стержня и их линии действия проходят через ось стержня (возникает поперечная сила и изгибающий момент).

n qz qz z N N+d. N dz dz

Нагрузочные функции: -сосредоточенная сила P при z a ФN(z)=0, при z a ФN(z)=P, а z -распределенная нагрузка q c z при z c ФN(z)=0, при z c ФN(z)=q(z-c),

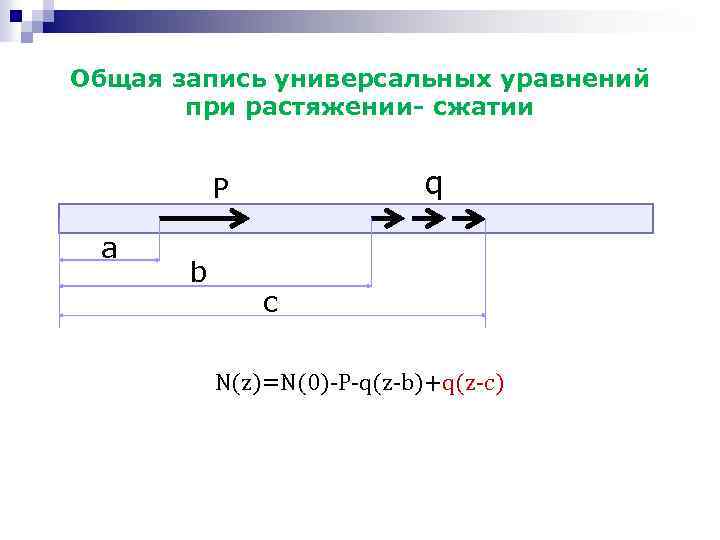Общая запись универсальных уравнений при растяжении- сжатии q P a b c N(z)=N(0)-P-q(z-b)+q(z-c)

Алгоритм решения задач по определению внутренних силовых факторов: n n Вводим систему координат – начало системы координат привязываем к крайнему левому сечению, ось Z направляем вдоль оси стержня, оси Х и У являются центральными осями сечения. Разбиваем стержень на участки. Участком называется отрезок оси стержня, на протяжении которого функция внутренних сил непрерывна. Границами участков является начало или конец стержня, начало или конец распределенной нагрузки, а так же точка приложения сосредоточенной нагрузки.

n n Раскладываем нагрузки в заданной системе координат и определяем вид нагружения. Записываем универсальное уравнение внутренних сил по участкам, начиная с силы или момента в нулевом сечении, затем на каждом участке добавляем только вновь появляющуюся нагрузку с противоположенным знаком. Используя, граничные условия определяем силу или момент в нулевом сечении. Граничным условием называется величина силы, момента или перемещения на краях стержня. Рассчитываем значение функции внутренних сил на границах участков и по полученным значениям строим график внутренних сил как функцию координаты сечения.

Задача: для заданной схемы нагружения построить график внутренних сил. P q l P=7 к. Н, q=10 к. Н/м, l=1 м. l

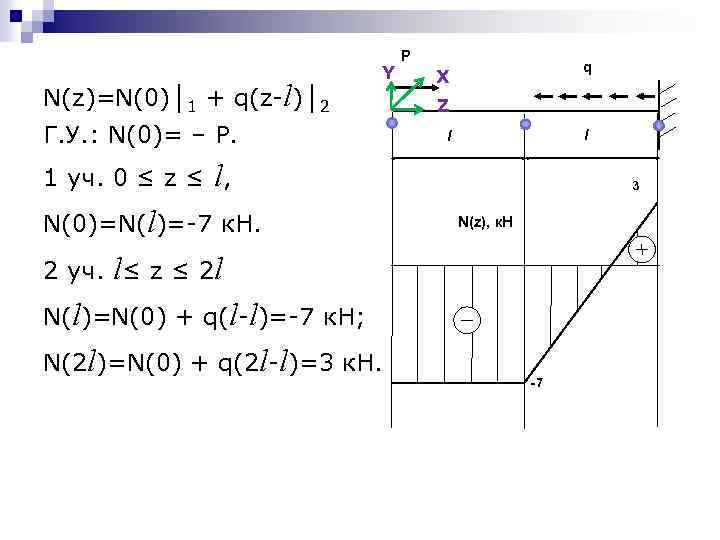N(z)=N(0)│1 + q(z-l)│2 Y Г. У. : N(0)= – Р. P q X Z l l 1 уч. 0 ≤ z ≤ l, N(0)=N(l)=-7 к. Н. 3 N(z), к. Н 2 уч. l≤ z ≤ 2 l N(l)=N(0) + q(l-l)=-7 к. Н; N(2 l)=N(0) + q(2 l-l)=3 к. Н. -7

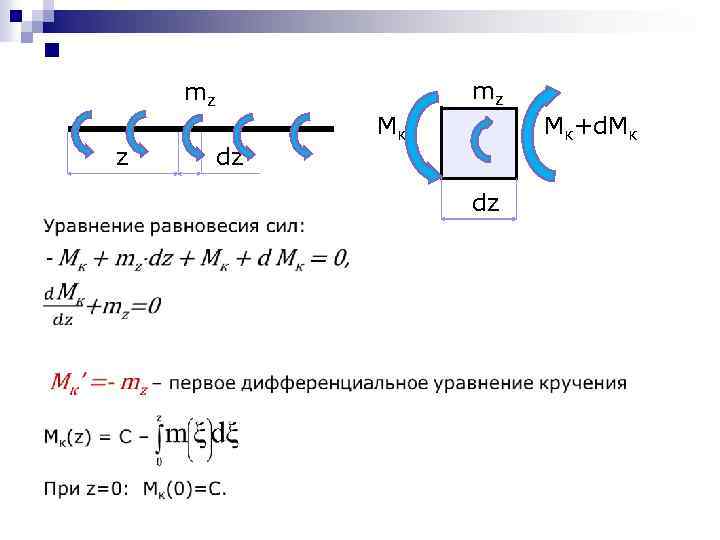n mz mz z dz Mк Mк+d. Mк dz

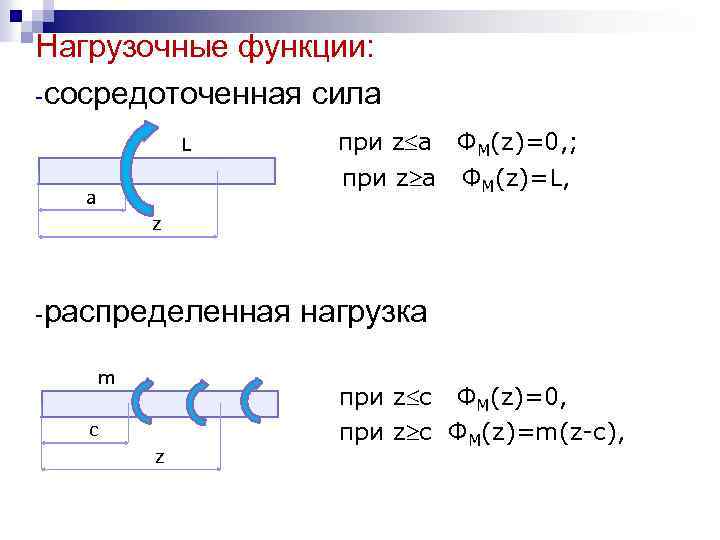Нагрузочные функции: -сосредоточенная сила при z a L ФM(z)=0, ; при z a ФM(z)=L, а z -распределенная нагрузка m c z при z c ФM(z)=0, при z c ФM(z)=m(z-c),

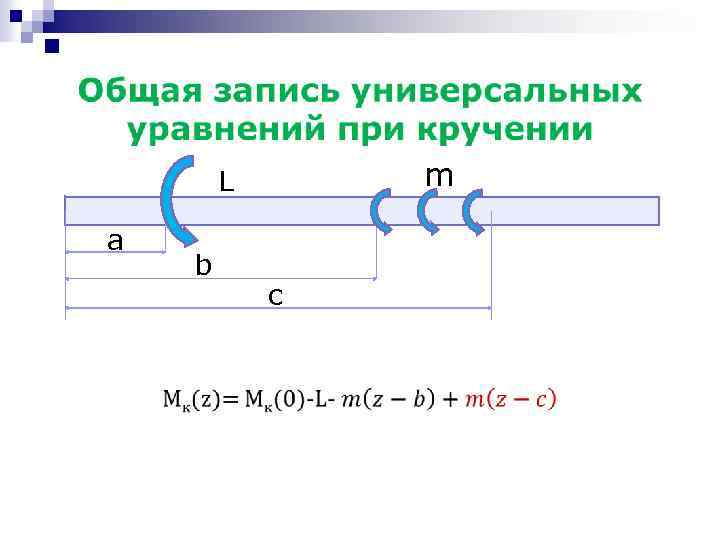n m L a b c

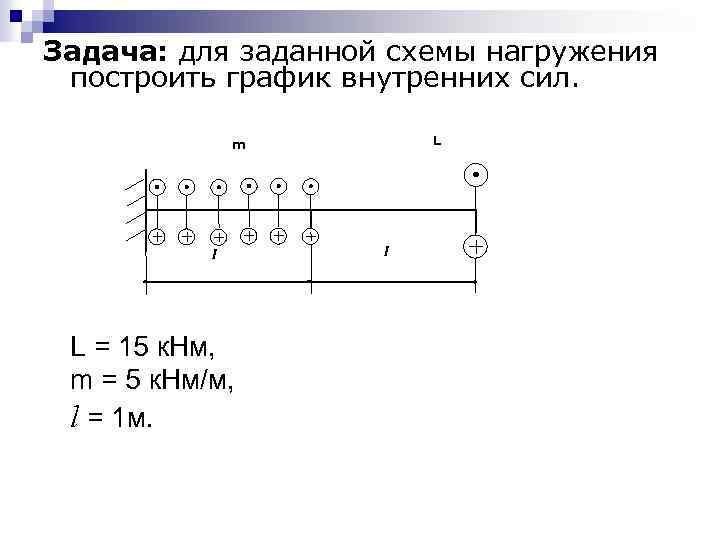Задача: для заданной схемы нагружения построить график внутренних сил. L m l L = 15 к. Нм, m = 5 к. Нм/м, l = 1 м. l

Y Mк(z)=Mк(0) – mz│1 + m(z-l)│2 Г. У. : Mк(2 l) = L. Mк(2 l)=Mк(0) – 2 ml + m(2 l-l)=L, Mк(0)= ml+L=20 к. Н·м. 1 уч. 0 ≤ z ≤ l, Mк(0)=20 к. Н·м; Mк(l)= Mк(0) – ml=15 к. Н·м. 2 уч. l≤ z ≤ 2 l Mк(l)= Mк(0) – ml=15 к. Н·м. Mк(2 l)= Mк(0) – 2 ml + m(2 l-l)=15 к. Н·м. X Z

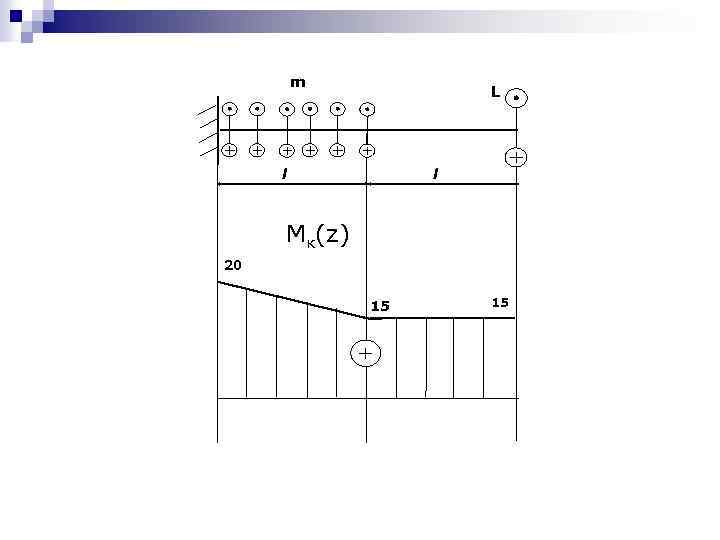m L l l Мк(z) 20 15 15

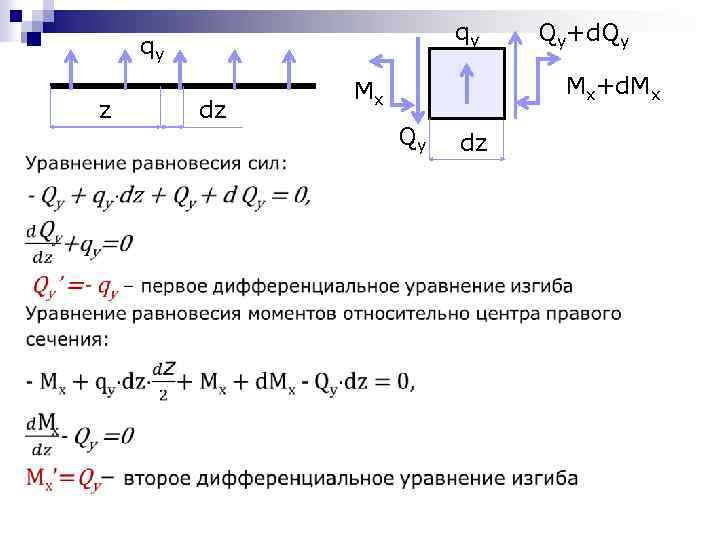n qy qу z dz Qy+d. Qy Mx+d. Mx Mx Qy dz

n

n P а z

n q c z

n L b z

n q P a b c d L

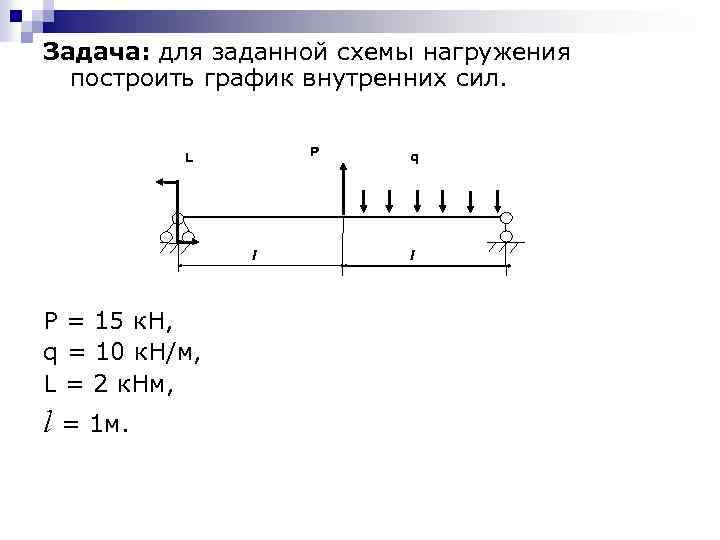Задача: для заданной схемы нагружения построить график внутренних сил. P L l Р = 15 к. Н, q = 10 к. Н/м, L = 2 к. Нм, l = 1 м. q l

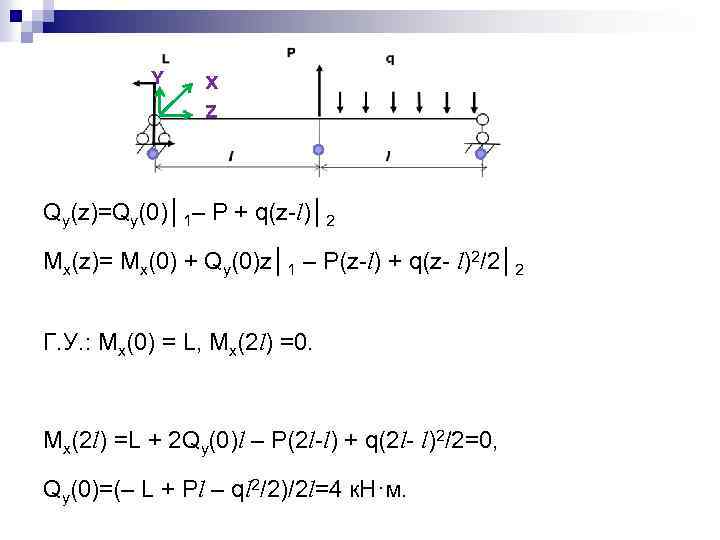Y X Z Qy(z)=Qy(0)│1– Р + q(z-l)│2 Mx(z)= Mx(0) + Qy(0)z│1 – P(z-l) + q(z- l)2/2│2 Г. У. : Mx(0) = L, Mx(2 l) =0. Mx(2 l) =L + 2 Qy(0)l – P(2 l-l) + q(2 l- l)2/2=0, Qy(0)=(– L + Pl – ql 2/2)/2 l=4 к. Н·м.

Qy(z)=Qy(0)│1– Р + q(z-l)│2 Mx(z)= Mx(0) + Qy(0)z│1 – P(z-l) + q(z- l)2/2│2 1 уч. 0 ≤ z ≤ l Qy(0)= Qy(l)= 4 к. Н; Mx(0)=L=2 к. Н·м; Mx(l)= Mк(0) + Qy(0)l=6 к. Н·м. 2 уч. l ≤ z ≤ 2 l Qy(l)= Qy(0) – Р + q(l-l)=-11 к. Н; Qy(2 l)= Qy(0) – Р + q(2 l-l)=-1 к. Н. Mx(l)= Mx(0)+Qy(0)l – P(l-l) + q(l-l)2/2=6 к. Н·м; Mx(2 l)=Mx(0)+Qy(0)2 l–P(2 l-l)+q(2 l-l)2/2=0.

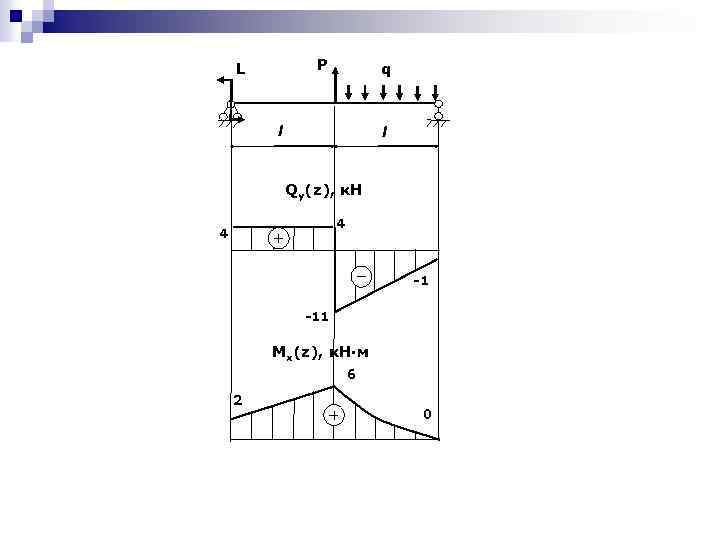P L q l l Qy(z), к. Н 4 4 -1 -11 Mx(z), к. Н·м 6 2 0

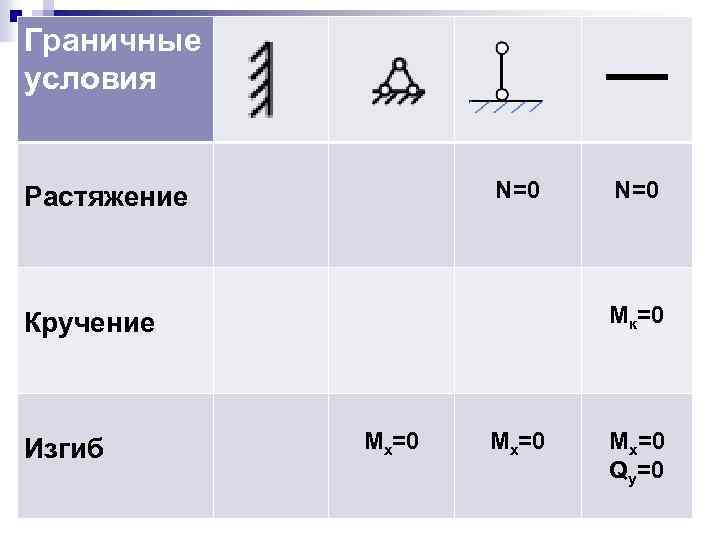Граничные условия N=0 Растяжение Mк=0 Кручение Изгиб N=0 Mx=0 Qy=0