Putting Light to Work for You Features of

Putting Light to Work for You Features of Signal Transfer

What have we learned? • Any traveling sinusoidal wave may be described by y = ym sin(kx wt + f) • f is the phase constant that determines where the wave starts. w = 2 pf = 2 p/T k = 2 p/l v = l/T = lf = w/k • Light always reflects with an angle of reflection equal to the angle of incidence (angles are measured to the normal).

What have we learned? • When light travels into a denser medium from a rarer medium, it slows down and bends toward the normal. • The amount light slows down in a medium is described by the index of refraction : n =c/v • The amount light bends is found by Snell’s Law: n 1 sin q 1 = n 2 sin q 2 • When the angle of refraction is 90 degrees, the angle of incidence is equal to the critical angle sin qc = n 2/n 1, where n 1 is for the denser medium

What else have we learned? • Light is trapped in an optical fiber if it strikes the sides of the fiber at angles greater than the critical angle for the core-cladding interface • The core must have a higher index of refraction than the cladding for total internal reflection to occur. • The numerical aperture (NA) of a fiber relates the maximum angle of incidence on the front of the fiber to the indices of refraction of the fiber: NA = n 0 sin qm = (n 12 - n 22)1/2.

Light in a waveguide • Light that strikes the side of the fiber at an angle less than the critical angle qc will escape • The angle that light strikes the side of the fiber depends on the angle q 0 at which light enters the fiber; the higher the angle at entrance, the lower the angle of incidence qi on the fiber wall n 0 q 0 n 2 qi n 1

Condition for TIR in waveguide • Snell’s Law (and some geometry) says n 0 sin q 0 = n 1 sin (90 - qi) = n 1 cos qi • If all of the beam is to stay within the waveguide, the angle of incidence on the wall must be greater than the critical angle: sin qc = n 2/n 1 • Then the angle at entrance must be obey n 0 sin q 0 < n 1 cos qc n 0 q 0 n 2 qi n 1

Numerical Aperture n 0 sin q 0 < n 1 cos qc • Using some trig (and the critical angle relationship) we see that the minimum angle of entrance qm is found from n 0 sin qm = n 1(1 - sin 2 qc)1/2 = n 1 (1 -n 22/n 12)1/2 = (n 12 - n 22)1/2. • The function n 0 sin qm is called the numerical aperture (NA) of the waveguide. • A large NA means light can enter in a large cone and still stay within the waveguide. n 0 q 0 n 2 qi n 1

Do the Fourier Series – Exploration part of the activity

Fourier Analysis • Waves we want to send are not always sinusoidal • BUT, Fourier showed that EVERY periodic function may be expressed as a sum of sine functions – Each term in the sum has a frequency equal to an integer times the frequency of the original function. • For example, a square wave is given by y(t) = (4/p) (sin wt + (1/3) sin 3 wt + (1/5) sin 5 wt + (1/7) sin 7 wt +. . . ) • Visual aids are best, so we go to CUPS (you’ll use it in part of your activity today, so pay attention!)

Do the Before You part of the activity Continue to the Fourier Series – Square Wave part

Fourier Transforms • Waves we want to send are not always periodic • BUT, Fourier showed that EVERY function may be expressed as an integral of sine functions – Non-periodic function is similar to infinite period, or infintesimal frequency – A sum over infintesimal steps (sin wt + sin 2 wt + …) is an integral • Visual aids are still best, so we again go to CUPS (you’ll use it in part of your activity today, so pay attention!)

Do the Fourier Transforms – Pulses part of the Activity

Why do we care about Fourier? • We want to send signals from one computer/phone/etc. to another one. • These signals will not be periodic if the message is to have any meaning. • Each Fourier component is subject to different interactions as it travels • Bandwidth is the range of frequencies that can travel through a medium • Large bandwidths are hard to transfer reliably

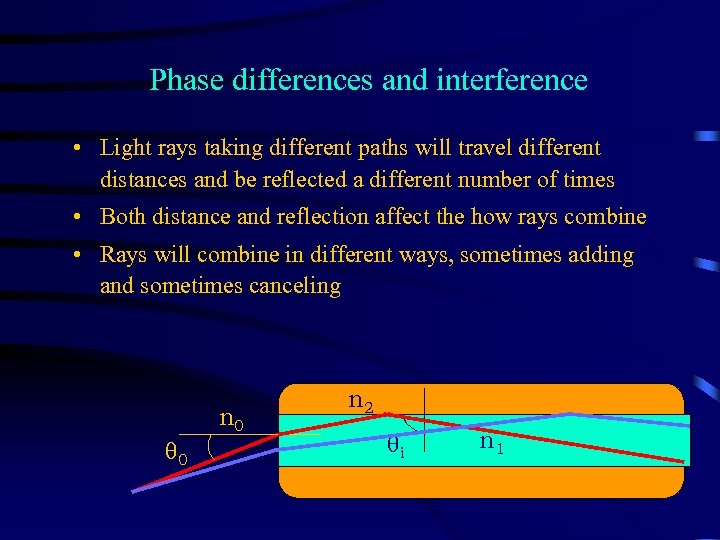Phase differences and interference • Light rays taking different paths will travel different distances and be reflected a different number of times • Both distance and reflection affect the how rays combine • Rays will combine in different ways, sometimes adding and sometimes canceling n 0 q 0 n 2 qi n 1

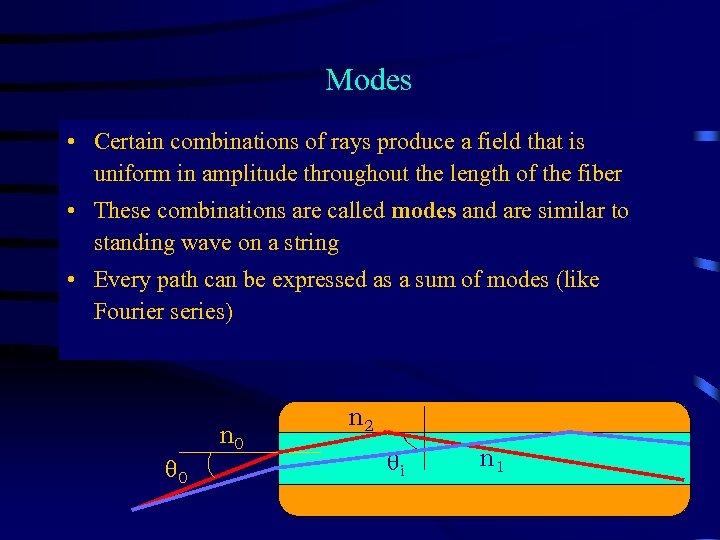Modes • Certain combinations of rays produce a field that is uniform in amplitude throughout the length of the fiber • These combinations are called modes and are similar to standing wave on a string • Every path can be expressed as a sum of modes (like Fourier series) n 0 q 0 n 2 qi n 1

Reducing the number of Modes • Different modes interact differently with the fiber, so modes will spread out, or disperse • If the fiber is narrow, only a small range of q 0 will be able to enter, so the number of modes produced will decrease • A small enough fiber can have only a single mode • BUT, you will lose efficiency because not all the light from the source enters the fiber. n 0 q 0 n 2 qi n 1

Optical waveguides pros and cons • Message remains private • Flexibility • Low Loss • Insensitive to EM interference BUT • Expensive to connect to every house • Require electricity-to-light converters • Either multi-modal, or less efficient

Dispersion • Index of refraction is dependent on wavelength. • Typical materials exhibit higher indices of refraction for lower wavelengths (higher energies) • Thus violet light bends the most through a prism or water and appears on the outside of a rainbow.

Before the next class, . . . • Read the Assignment on Describing Signals found on Web. CT • Read Chapter 4 from the handout from Grant’s book on Lightwave Transmission • Do Reading Quiz 4 which will be posted on Web. CT by Tuesday morning. • Finish Homework 2, due Thursday • Do Activity 04 Evaluation by Midnight Monday