Пути вскрытия RSA Полиномиально эквиваленты Дано п е

Пути вскрытия RSA Полиномиально эквиваленты Дано: п, е, emod п М Факторизация модуля Найти: М п Задача RSA Вычисление функции φ (п ) Расчет закрытой экспоненты d=е-1 modφ(n)

L-нотация для обозначения сложности алгоритмов факторизации чисел ε(log N)1 -ε (c+О(1))(log 2 N) 2 2 e LN (ε, c) = ε =0 ПОЛИНОМИАЛЬНЫЙ ε =1 ЭКСПОНЕНЦИАЛЬНЫЙ 0<ε<1 CУБЭКСПОНЕНЦИАЛЬНЫЙ Эффективны Не эффективны Чем ближе ε к 0, тем алгоритм более эффективен

Наиболее эффективные алгоритмы факторизации Квадратичное решето Факторизация на эллиптических кривых LN ( , 1) = )= e LN ( Общий метод LN ( решета числового поля (1+О(1))(log 2 N·log 2 N)1/2 e (1+О(1))(2 log 2 р·log 2 p)1/2 р – наименьший множитель числа N )= = (1, 92+О(1))(log 2 N 1/3 ·log 2 N)2/3 e

Последние результаты факторизации больших чисел поля ого то числов реше Числовое поле быстрее для очень больших чисел Для RSA квадратичное решето лучше, чем эллиптические кривые Квадратичное решето работает для чисел не больше 10110 с простым делителем, меньшим

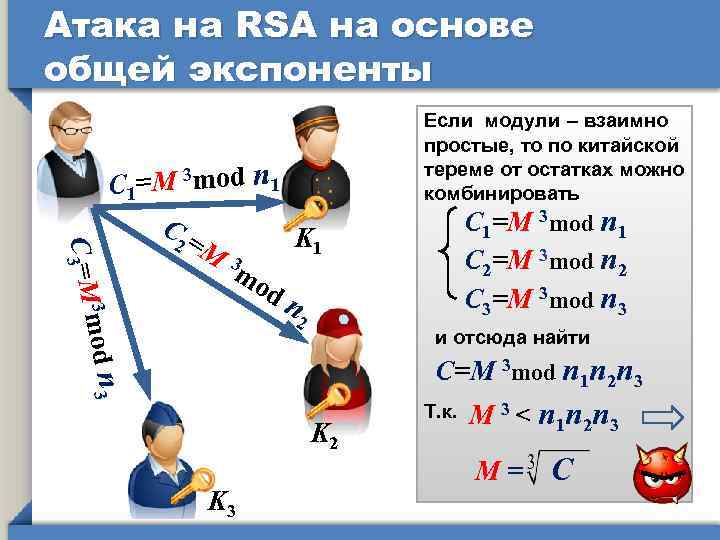Атака на RSA на основе общей экспоненты п 2 3 mod С 3=M С 1=M 3 mod п 1 С K 1 2 =M 3 mo d Если модули – взаимно простые, то по китайской тереме от остатках можно комбинировать С 1=M 3 mod п 1 С 2=M 3 mod п 2 С 3=M 3 mod п 3 и отсюда найти п 3 С=M 3 mod п 1 п 2 п 3 K 2 K 3 Т. к. M 3 < п 1 п 2 п 3 M= С

Атака на RSA на основе общего модуля С 1=M t 1=e 1 -1 mod e 2 е 1 mod п t 2= (t 1 e 1 -1)/e 2 е 2 m =M С 2 K 1 t 1 e 1= t 2 e 2+1, t 2Є Z od M = C 1 t 1 C 2 -t 2 mod n п K 2 Почему?

Атака на RSA : «встреча посередине» Мультипликативность: е С 1≡M 1 mod п е С 2≡M 2 mod п Каким будет шифротекст открытого текста M=M 1 M 2 ? е е е С≡(M 1 M 2) =M 1 M 2 mod п=С 1 С 2 -e е С·M 1 =M 2 mod п можно построить атаку Пусть известно, что M=M 1 M 2< 2 L/2

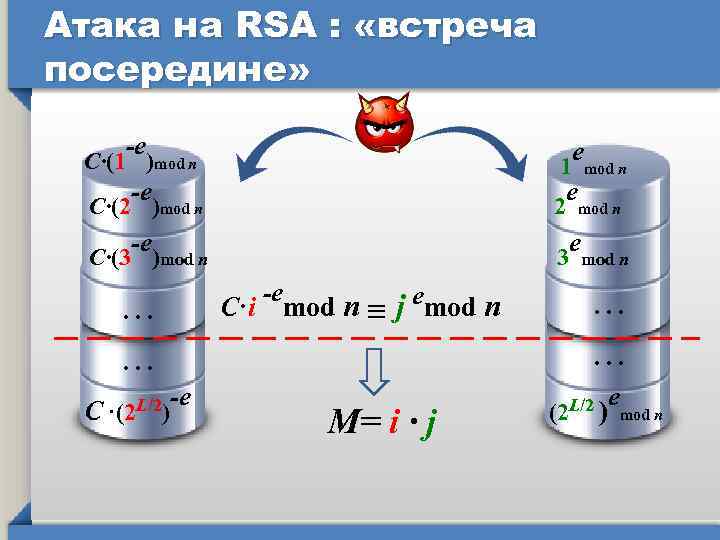Атака на RSA : «встреча посередине» -е е С·(1 )mod п 1 -е е С·(2 )mod п 2 -е 3 -е С·i mod п ≡ j emod n . . . mod п . . С ·(2 L/2) mod п е С·(3 )mod п -e M= i · j (2 L/2 ) е mod п

Циклическая атака на RSA (бесключевое чтение) е С ≡С 1 mod п е С 1 ≡С 2 mod п е С 2 ≡С 3 mod п … е Сk-2 ≡Сk-1 mod п е Сk-1 ≡Сkmod п ≡ C Атака успешна, если порядок k открытой експоненты e мал (k – наименьшее число, для которого еk≡ 1(modφ(n)); НОД(e, φ(n))=1) М = Сk-1

Атака Винера: математическое вступление ЦЕПНЫЕ (НЕПРЕРЫВНЫЕ) ДРОБИ Любое действительное число х можно представить цепной дробью x = [a 0; a 1, a 2, …] 1 = a 0+ a 1 + a 2 + 1 1 ∩ а 0 Z; а 1, а 2, … ∩ a 3 + N …

Атака Винера: математическое вступление Как найти элементы цепной дроби для числа х ? x 0 = x – a 0 1 а 1= x 0 1 а 2= x 1 ; ; 1 x 1= x – a 1 ; 0 ; 1 x 2= x – a 2 ; 1 1 аi = x i– 1 . . . ; 1 xi = x – ai ; i– 1 x -целая часть числа х

Атака Винера: математическое вступление Пример. Найти разложение в цепную дробь числа x = 34 99 34 = 0 ; x = x – a = 34 Решение. а 0= x = 0 0 99 1 99 = 34 =2; 1 – a = 99 – 2 = 31 x 1= x 1 34 34 0 а 2= 1 = 34 = 1 ; x 1 31 x 2= 1 – a 2 = 34 – 1 = 3 x 1 31 31 а 1= x 0 а 3= 1 = 31 = 10 ; x 3= 1 – a 3 = 31 – 10 = 1 x 2 3 3 а 4= 1 = 3 x 3 1 =3

Атака Винера: математическое вступление x = 34 = [0; 2, 1, 10, 3]= 0+ 99 1 1 2+ 1 1+ 10 + 1 3

Атака Винера: математическое вступление pi і-ой подходящей дробью для цепной дроби qi x = [a 0; a 1, a 2, …] p называют конечную цепную дробь i = [a ; a , …, a ] 0 1 2 i qi Рекуррентные формулы для вычисления подходящих pi дробей для цепной дроби qi = [a 0; a 1, a 2, …, ai] : p– 1 = 1; q– 1 = 0; p 0 = a 0 ; q 0 = 1 pi ai pi – 1 + pi – 2 qi = ai qi – 1 + qi – 2 ; i = 1, 2, …

Атака Винера: математическое вступление Пример. Найти подходящие дроби для цепной дроби 34 99 = [0; 2, 1, 10, 3] Решение. [0; 2, 1, 10, 3] a 0 a 1 a 2 a 3 a 4 p– 1 = 1; p 0 = 0 ; p 1 q 1 = a 1 q– 1 = 0; q 0 = 1 p 0 + p– 1 2· 0+1 1 = 2· 1+0 = 2 q 0 + q– 1 p 2 a 2 p 1 + p 0 1· 1+0 1 q 2 = a 2 q 1 + q 0 = 1· 2+1 = 3 ; ; p 1 = 1; q 1 = 2; p 2 = 1; q 2 = 3;

Атака Винера: математическое вступление p 3 a 3 p 2 + p 1 10· 1+1 11 = = 10· 3+2 = 32 ; q 3 a 3 q 2 + q 1 p 3 = 11; q 3 = 32; p 4 q 4 = p 4 = 34; q 4 = 99 a 4 p 3 + p 2 3· 11+1 34 = 3· 32+2 = 99 ; a 4 q 3 + q 2 Подходящие дроби: p 1 1 q 1 = 2 ; p 2 1 q 2 = 3 ; p 3 11 p 4 34 q 3 = 32 ; q 4 = 99 ;

Атака Винера: математическое вступление p Если несократимая дробь удовлетворяет q неравенству: p x– ≤ 1 2 q 2 q p то дробь – одна из подходящих дробей в q разложении числа х в цепную дробь.

Атака Винера М. Винер показал, что когда секретная экспонента e n e – k 1 ≤ d n 2 d 2 то дробь удовдетворяет неравенству • это классическая аппроксимация с помощью цепных дробей; k d

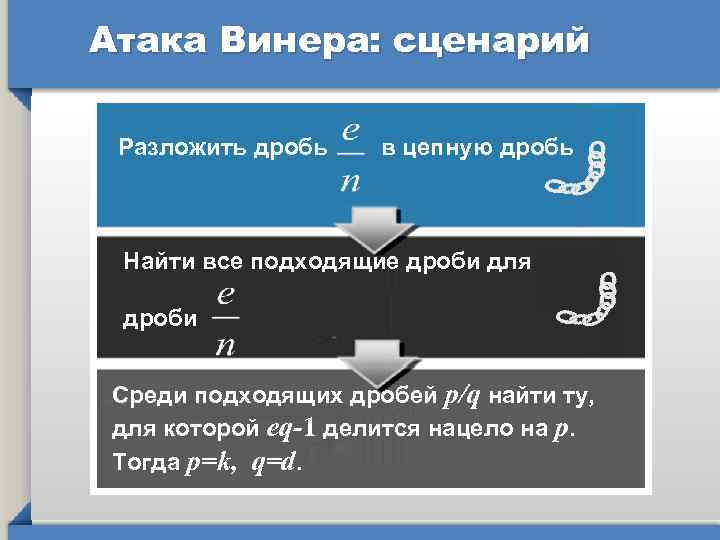Атака Винера: сценарий Разложить дробь в цепную дробь Найти все подходящие дроби для дроби Среди подходящих дробей p/q найти ту, для которой eq-1 делится нацело на р. Тогда p=k, q=d.

Атака Винера: противодействие Для противодействия атаке надо, чтобы секретная экспонента была не меньше, чем 0, 292 п Например, если модуль имеет размер 1024 бит, 1024 необходимо чтобы длина секретной экспоненты была не менее 256 бит. 256

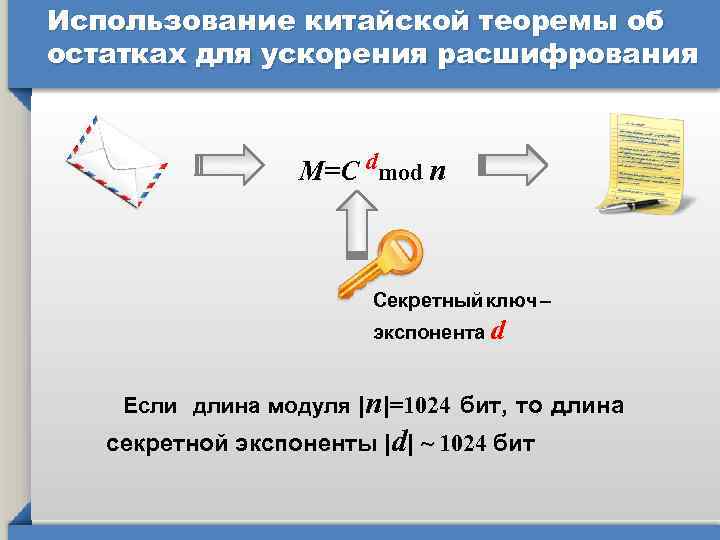Использование китайской теоремы об остатках для ускорения расшифрования M=С dmod п Секретный ключ – экспонента d Если длина модуля |n|=1024 бит, то длина секретной экспоненты |d| ~ 1024 бит

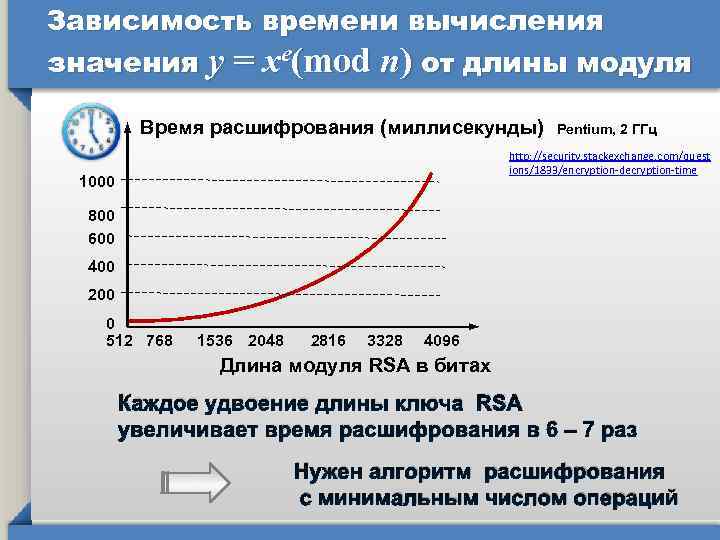Зависимость времени вычисления значения у = хe(mod n) от длины модуля Время расшифрования (миллисекунды) Pentium, 2 ГГц http: //security. stackexchange. com/quest ions/1833/encryption-decryption-time 1000 800 600 400 200 0 512 768 1536 2048 2816 3328 4096 Длина модуля RSA в битах Каждое удвоение длины ключа RSA увеличивает время расшифрования в 6 – 7 раз Нужен алгоритм расшифрования с минимальным числом операций

Использование китайской теоремы об остатках для ускорения расшифрования Владелец секретного ключа знает p и q Mp≡С dmod p≡С d mod p-1 mod p Mq≡С dmod q≡С d mod q-1 mod q По китайской теореме об остатках M ≡ Mp mod p M ≡ Mq mod q Если длина модуля |n|=1024 бит, то длины множителей |р|= |q| = 512 бит

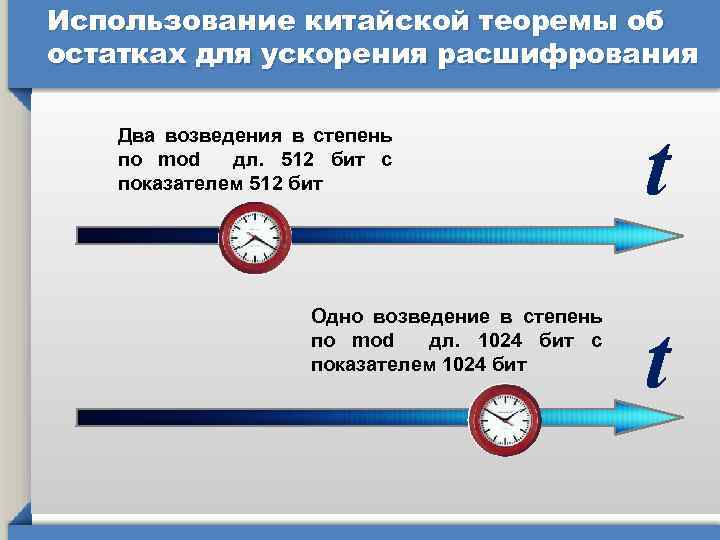Использование китайской теоремы об остатках для ускорения расшифрования Два возведения в степень по mod дл. 512 бит c показателем 512 бит Одно возведение в степень по mod дл. 1024 бит c показателем 1024 бит t t

Симметричные против асимметричных криптосистем Стойкие, работают очень быстро. Им не нужны большие вычислительные ресурсы. При передаче ключа он может быть перехвачен мошенником Асимметричные алгоритмы очень медленные Распространяют открытые ключи открыто. Перехват открытых ключей – бесполезен.

Гибридные криптосистемы

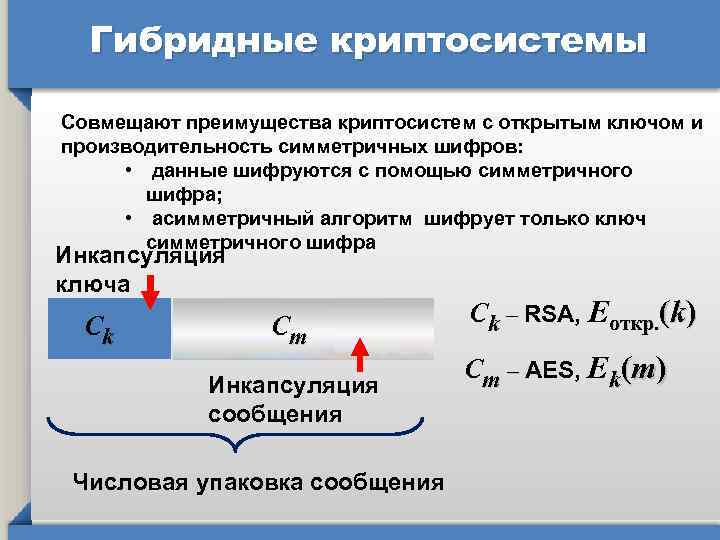Гибридные криптосистемы Совмещают преимущества криптосистем с открытым ключом и производительность симметричных шифров: • данные шифруются с помощью симметричного шифра; • асимметричный алгоритм шифрует только ключ симметричного шифра Инкапсуляция ключа Сk Сm Инкапсуляция сообщения Числовая упаковка сообщения Сk – RSA, Eоткр. (k) Сm – AES, Ek(m)

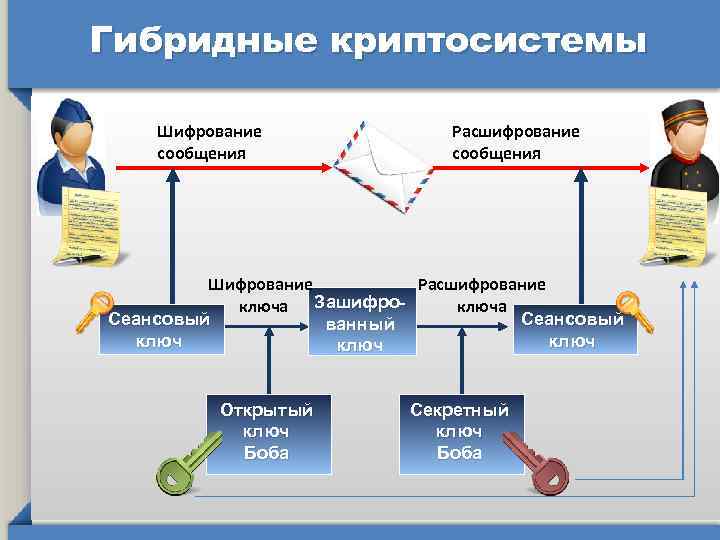Гибридные криптосистемы Шифрование сообщения Расшифрование сообщения Шифрование Расшифрование ключа Зашифроключа Сеансовый ванный ключ Открытый ключ Боба Секретный ключ Боба