Pulsed-Power Plasma and its Applications Yakov Krasik Physics

Pulsed-Power Plasma and its Applications Yakov Krasik Physics Department, Technion • Pulsed Power • Plasma cathodes for relativistic high-current electron beams • Microwave generation • Underwater electrical wire explosion • Generation of converging strong shock waves

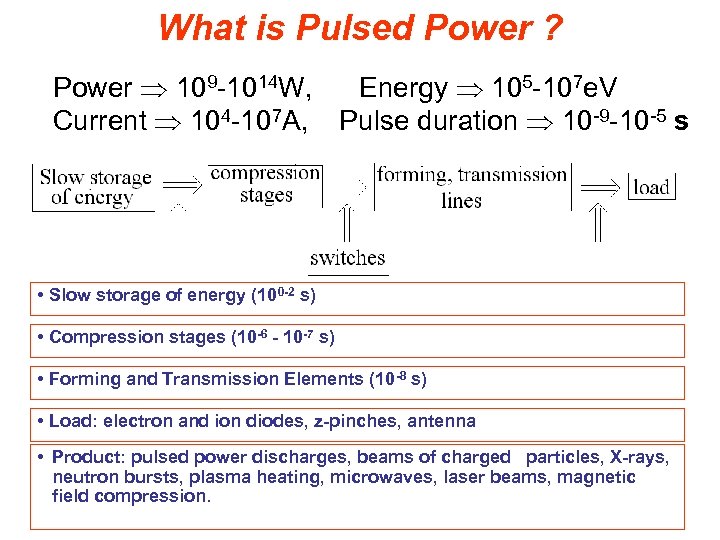What is Pulsed Power ? Power 109 -1014 W, Energy 105 -107 e. V Current 104 -107 A, Pulse duration 10 -9 -10 -5 s • Slow storage of energy (100 -2 s) • Compression stages (10 -6 - 10 -7 s) • Forming and Transmission Elements (10 -8 s) • Load: electron and ion diodes, z-pinches, antenna • Product: pulsed power discharges, beams of charged particles, X-rays, neutron bursts, plasma heating, microwaves, laser beams, magnetic field compression.

Pulsed Power Applications • High-Power Bremsstrahlung Sources (Electron beams) Dose ~ Ee 2. 8 Ie (HERMES III: 20 Me. V, 700 k. A, 30 ns 100 k. Rad at 500 cm 2) • High Intensity Neutron Fluxes ( Ion beam 1013 1 n 0/pulse) • Strong Shock Wave Generation (electron and ion beams) Pressure ~ Pb /(S ); Pb ~ 1013 W/cm 2 Pressure ~ 10 Mbar • High-Power Microwaves (Microwave power 10 GW) • High-Power Pulsed Gaseous Lasers • Strengthening and Modification of Materials • Thin Film Preparation

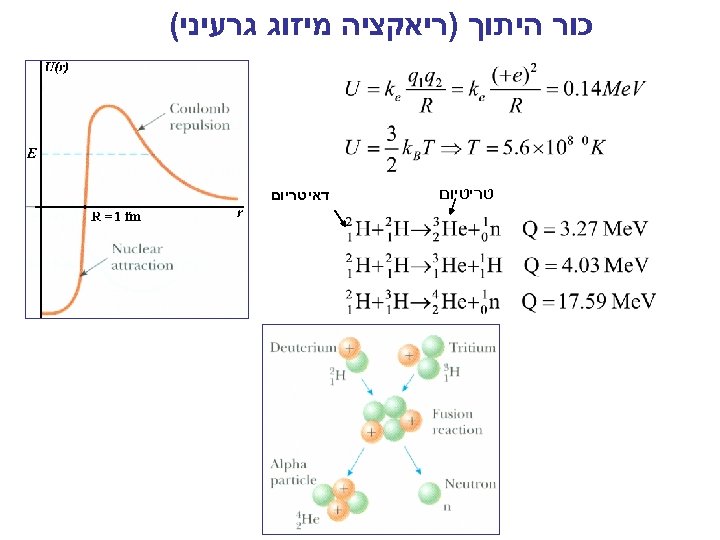כור היתוך )ריאקציה מיזוג גרעיני( טריטיום דאיטריום

Confinement Fusion 2 H 1 +3 H 1 4 He 2 (3. 6 Me. V)+1 n 0 (14 Me. V) [Energy: 1 kg 1014 J] The volume rate of fusion reactions: Confinement time International Thermonuclear (Tokamak) Experimental Reactor: ITER [ 2015 (2021)] n 1014 cm-3; T 10 ke. V; 400 s; Pin = 40 MW; Pout = 500 MW (0. 5 g D-T in 840 m 3 volume) Plasma major radius: 6. 2 m; Plasma minor radius: 2 m Plasma current – 15 MA; Average neutron flux: 0. 5 MW/m 2 Magnetic field at axis: 5. 3 T Toroidal magnetic field energy – 4 1010 J

Inertial Confinement Fusion Confinement time: time it takes sound waves to travel across the plasma Adiabatic compression: Solid DT: 0. 2 g/cm 3. Compression: 104. R=0. 1 mm. Pressure: 106 bar. Energy: 106 J. Power: 1014 W/cm 2 Electron/Ion/Laser beams or soft x-rays rapidly heat the surface of the fusion target forming a surrounding plasma layer Compression Target is compressed by plasma expansion Ignition The fuel core reaches 104 of T-D density and ignites at 10 ke. V Burn Thermonuclear burn spreads through the compressed T-D, yielding the input energy. • Electron Beams • Laser Beams (NIF: Lawrence Livermore National Lab) • Soft X-rays (Z-pinch: Sandia National Lab) • Ion Beams

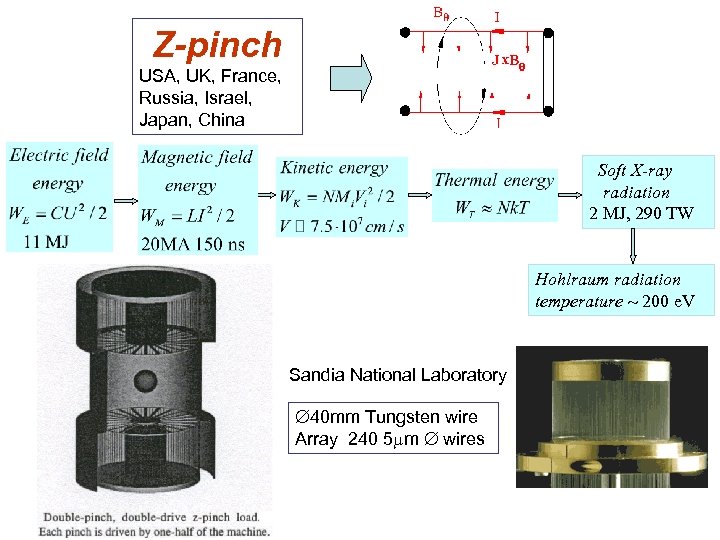Z-pinch USA, UK, France, Russia, Israel, Japan, China Soft X-ray radiation 2 MJ, 290 TW Hohlraum radiation temperature 200 e. V Sandia National Laboratory 40 mm Tungsten wire Array 240 5 m wires

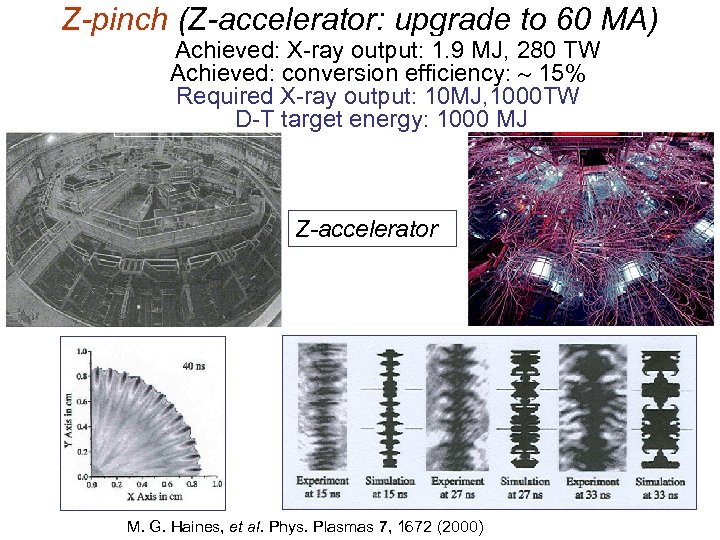Z-pinch (Z-accelerator: upgrade to 60 MA) Achieved: X-ray output: 1. 9 MJ, 280 TW Achieved: conversion efficiency: 15% Required X-ray output: 10 MJ, 1000 TW D-T target energy: 1000 MJ Z-accelerator M. G. Haines, et al. Phys. Plasmas 7, 1672 (2000)

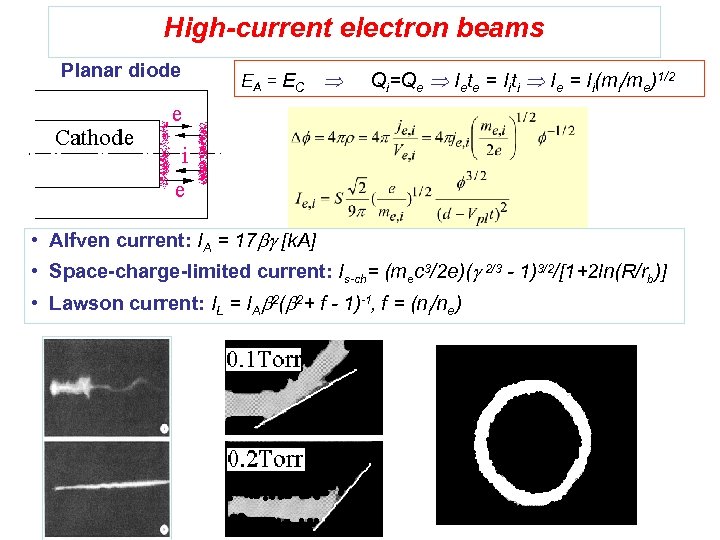High-current electron beams Planar diode EA = EC Qi=Qe Iete = Iiti Ie = Ii(mi/me)1/2 • Alfven current: IA = 17 bg [k. A] • Space-charge-limited current: Is-ch= (mec 3/2 e)(g 2/3 - 1)3/2/[1+2 ln(R/rb)] • Lawson current: IL = IAb 2(b 2+ f - 1)-1, f = (ni/ne)

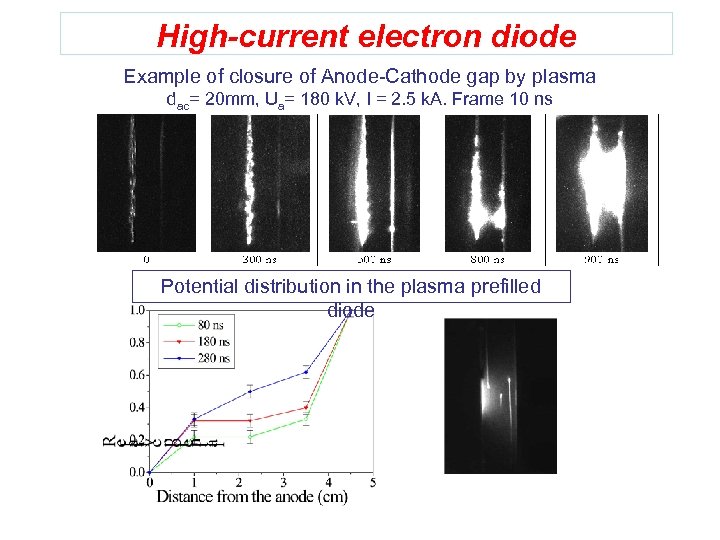High-current electron diode Example of closure of Anode-Cathode gap by plasma dac= 20 mm, Ua= 180 k. V, I = 2. 5 k. A. Frame 10 ns Potential distribution in the plasma prefilled diode

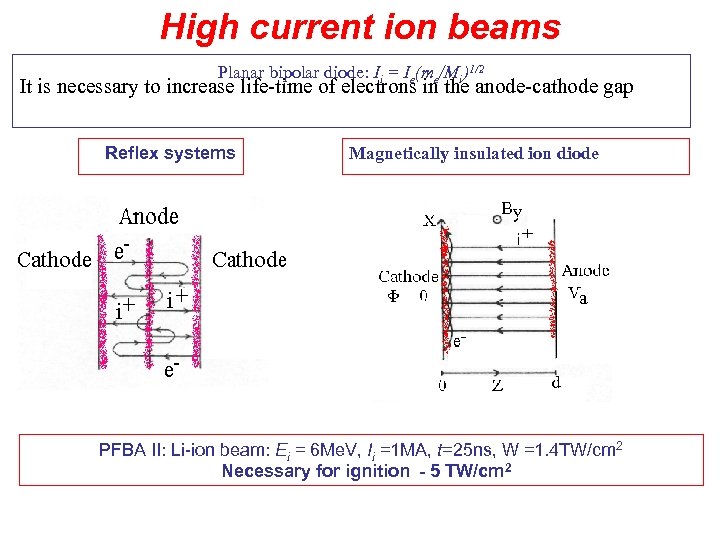High current ion beams Planar bipolar diode: Ii = Ie(me/Mi)1/2 It is necessary to increase life-time of electrons in the anode-cathode gap Reflex systems Magnetically insulated ion diode PFBA II: Li-ion beam: Ei = 6 Me. V, Ii =1 MA, t=25 ns, W =1. 4 TW/cm 2 Necessary for ignition - 5 TW/cm 2

Explosive Emission Plasma

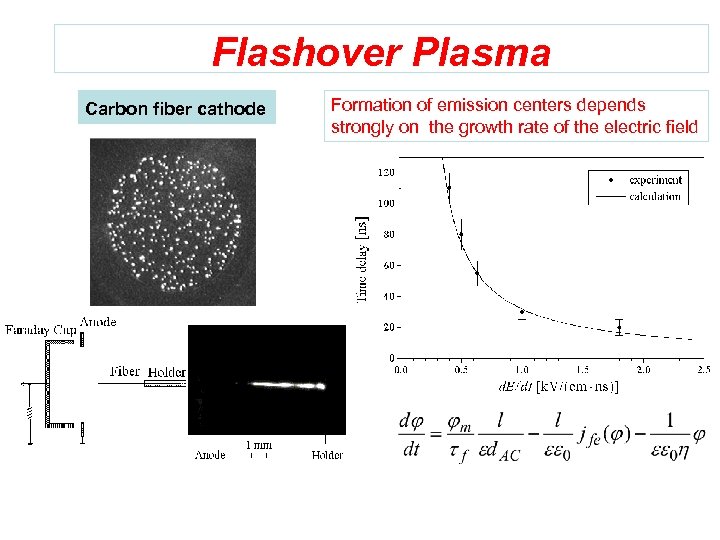Flashover Plasma Carbon fiber cathode Formation of emission centers depends strongly on the growth rate of the electric field

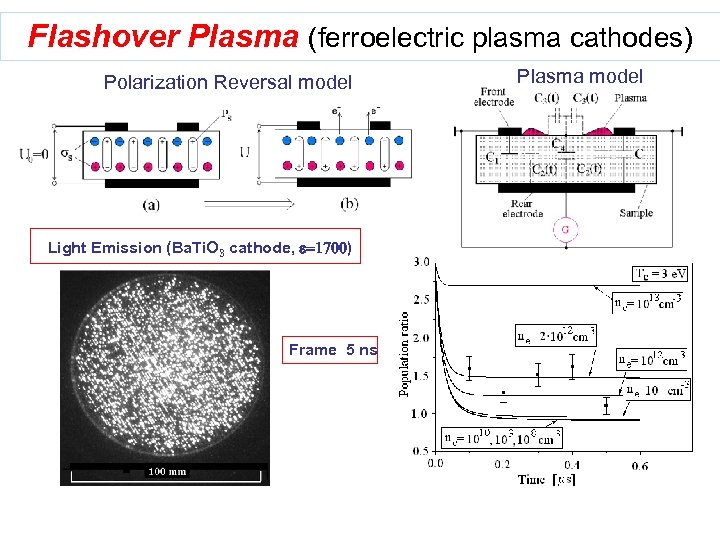Flashover Plasma (ferroelectric plasma cathodes) Polarization Reversal model Light Emission (Ba. Ti. O 3 cathode, e=1700) Frame 5 ns Plasma model

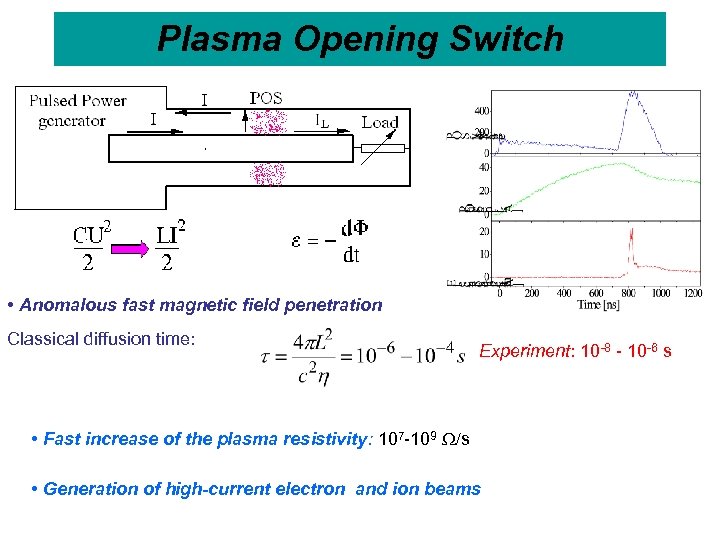Plasma Opening Switch • Anomalous fast magnetic field penetration Classical diffusion time: Experiment: 10 -8 - 10 -6 s • Fast increase of the plasma resistivity: 107 -109 W/s • Generation of high-current electron and ion beams

Anomalous fast magnetic field penetration • Electron Magnetohydrodynamics (Hall effect ) • • Current channel: d >> (c/wpe) ? ? ? • Energy dissipation mechanism ? ? ?

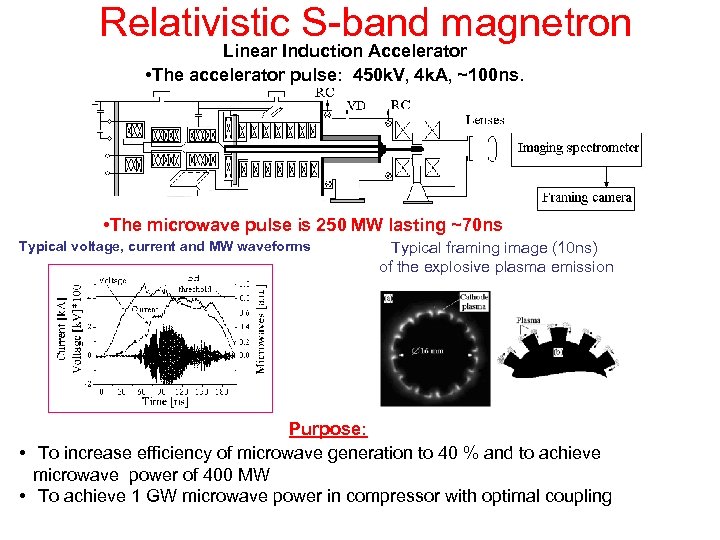Relativistic S-band magnetron Linear Induction Accelerator • The accelerator pulse: 450 k. V, 4 k. A, ~100 ns. • The microwave pulse is 250 MW lasting ~70 ns Typical voltage, current and MW waveforms Typical framing image (10 ns) of the explosive plasma emission Purpose: • To increase efficiency of microwave generation to 40 % and to achieve microwave power of 400 MW • To achieve 1 GW microwave power in compressor with optimal coupling

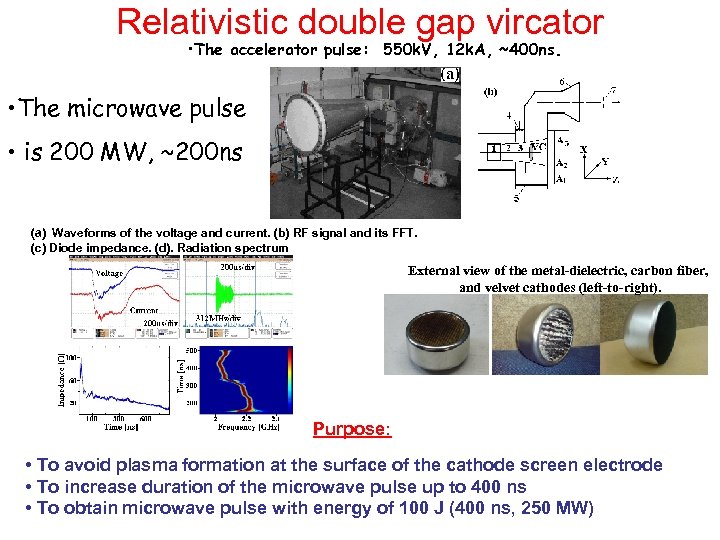Relativistic double gap vircator • The accelerator pulse: 550 k. V, 12 k. A, ~400 ns. • The microwave pulse • is 200 MW, ~200 ns (a) Waveforms of the voltage and current. (b) RF signal and its FFT. (c) Diode impedance. (d). Radiation spectrum External view of the metal-dielectric, carbon fiber, and velvet cathodes (left-to-right). Purpose: • To avoid plasma formation at the surface of the cathode screen electrode • To increase duration of the microwave pulse up to 400 ns • To obtain microwave pulse with energy of 100 J (400 ns, 250 MW)

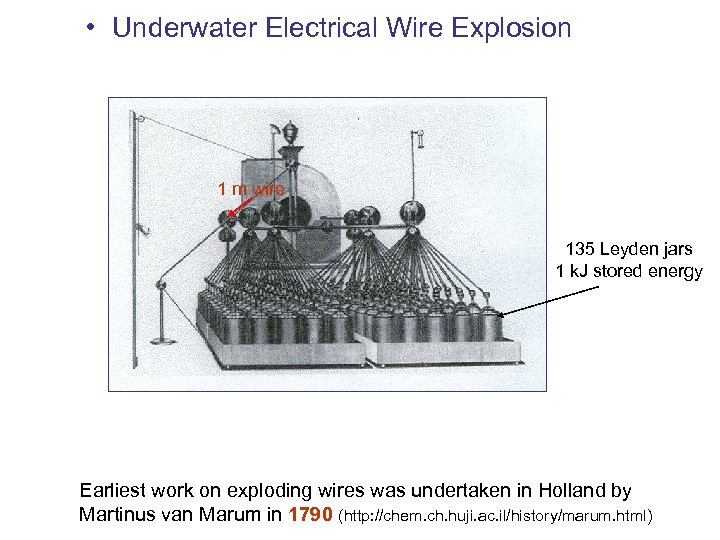• Underwater Electrical Wire Explosion 1 m wire 135 Leyden jars 1 k. J stored energy Earliest work on exploding wires was undertaken in Holland by Martinus van Marum in 1790 (http: //chem. ch. huji. ac. il/history/marum. html)

Wire electrical explosion – a spiky change in the physical state of the metal as a result of intense energy input due to pulsed current with density >106 A/cm 2 Current density: 106 – 1010 A/cm 2. Current pulse duration: 10 -4 – 10 -8 s. Power: 106 – 1013 W. Delivered Energy: 102 – 106 J Background medium: vacuum, gas, liquid Flash Lamp, Time Delay Generator Wire explosion in water Laser The wire HV Pulse Generator Two frame (5 ns) images with 300 ns interval Shock waves Mirror Streak or Framing Camera + CCD Discharge plasma channel

Basic Fundamental Research • Ultra-fast heating of metals: d. T/dt > 1011 0 K/s • Magnetic field: 107 G Energy density: 1011 J/m 3 Phase transitions: solid state liquid gas plasma Equations of State at extreme conditions (pressure: Mbar, temperature: 104 K) Pressure Density Temperature Conductivity Internal energy Thermal conductivity • Non-ideal plasma (high density, low temperature) Potential energy of Coulomb interaction Thermal energy Classical plasma Resistivity and thermal conductivity – differ strongly from the case of ideal plasma V. Fortov and I. T. Iakubov, The Physics of Non-Ideal Plasma ( World Scientific Publ. , NJ, 2000)

Applications • High-power radiation sources (visible, UV range) : P >109 W • Lasers ( 1000 Ǻ) & Pumping of gaseous and ruby lasers (intensity an order of magnitude greater than that obtained from Xe flash lamps) • Pulsed neutron source [CD 2 or Li. D wires: up to 1012 1 n 0/pulse: NRL (650 k. A, 100 ns)] • Nano particles (1 – 100 nm) of different metals • Shock waves: underwater electrical wire explosion • High-current opening switch (high-voltage generator) • Powerful soft x-ray sources (Lebedev Physical Institute, Cornell University) Current : 300 k. A, 100 ns • Point-like source 10 m • Time duration 10 ps – 200 ps • Soft x-ray energy 2 – 15 ke. V • Hard x-ray energy 25 - 80 ke. V

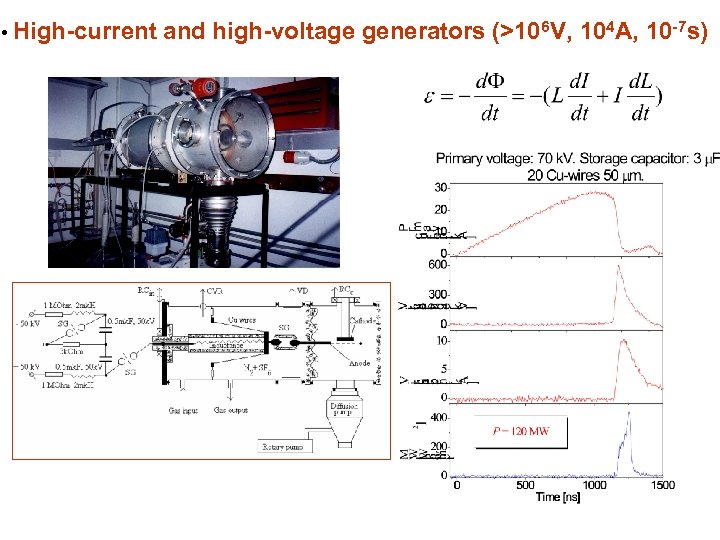• High-current and high-voltage generators (>106 V, 104 A, 10 -7 s)

Main Obstacles in Electrical Wire Explosion in vacuum/gas 1. Shunting of the Discharge. The best energy deposition in vacuum recently achieved by Sarkisov et al. * was 20 times the atomization enthalpy. 2. Fast plasma expansion ( 107 cm/s) in vacuum limits energy density input 3. Radiation cooling in vacuum wire explosion limits plasma temperature 4. Fast growing plasma instabilities and charged particle emission

Underwater Electrical Wire Explosion (UEWE) Ø High Density Non-Ideal Plasma Ø Ultra High Pressure at the axis of Converging Cylindrical Shock Wave produced by Underwater Electrical Wire Array Explosion Advantages of the Underwater Electrical Wire Explosion Shunting of the discharge is prevented due to: 1. High breakdown voltage of the water medium (>300 k. V/cm). 2. High pressure of the adjacent water layer (>10 k. Bar) increases breakdown voltage. Increase in the temperature of the wire plasma is achieved by: 1. High resistance of the water to compression limits the wire expansion and leads to the increase in the current density. 2. Substantial decrease in the energy loss to the shunting channel and to radiation (water “bath” effect).

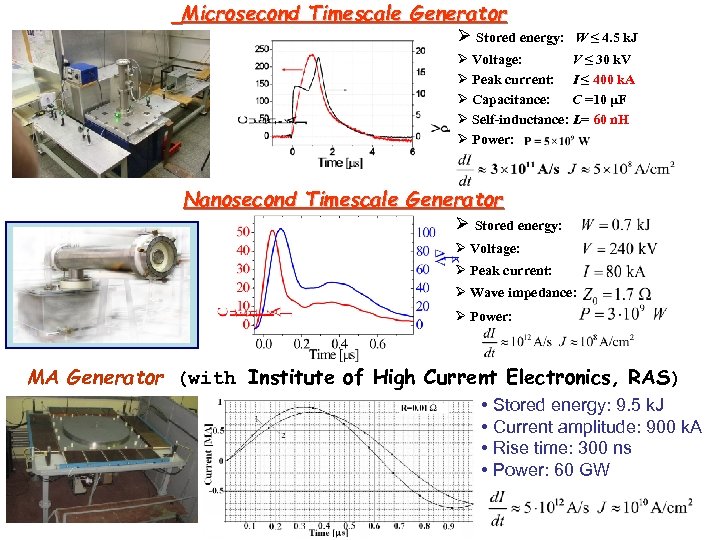Microsecond Timescale Generator Ø Stored energy: W ≤ 4. 5 k. J Ø Voltage: V ≤ 30 k. V Ø Peak current: I ≤ 400 k. A Ø Capacitance: C =10 μF Ø Self-inductance: L= 60 n. H Ø Power: Nanosecond Timescale Generator Ø Stored energy: Ø Voltage: Ø Peak current: Ø Wave impedance: Ø Power: MA Generator (with Institute of High Current Electronics, RAS) • Stored energy: 9. 5 k. J • Current amplitude: 900 k. A • Rise time: 300 ns • Power: 60 GW

Diagnostics Tools • Electrical probes: voltage & current monitors • Electro – mechanical pressure gauges • Optical: Schlieren & Shearing Interferometry • Fast streak and frame shadow imaging • Fast photodiodes & narrow band interference filters • Visible range spectroscopy

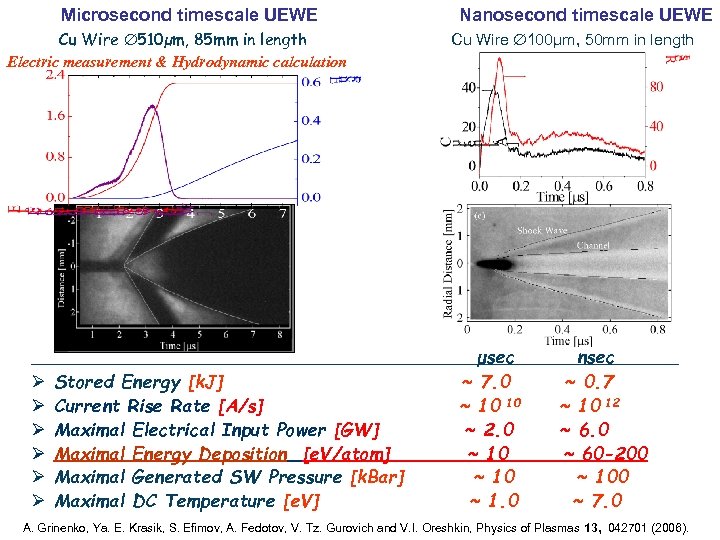Microsecond timescale UEWE Cu Wire 510µm, 85 mm in length Electric measurement & Hydrodynamic calculation Nanosecond timescale UEWE Cu Wire 100µm, 50 mm in length μsec ~ 7. 0 ~ 10 10 ~ 2. 0 ~ 10 ~ 1. 0 nsec Ø Stored Energy [k. J] ~ 0. 7 Ø Current Rise Rate [A/s] ~ 10 12 Ø Maximal Electrical Input Power [GW] ~ 6. 0 Ø Maximal Energy Deposition [e. V/atom] ~ 60 -200 Ø Maximal Generated SW Pressure [k. Bar] ~ 100 Ø Maximal DC Temperature [e. V] ~ 7. 0 A. Grinenko, Ya. E. Krasik, S. Efimov, A. Fedotov, V. Tz. Gurovich and V. I. Oreshkin, Physics of Plasmas 13, 042701 (2006).

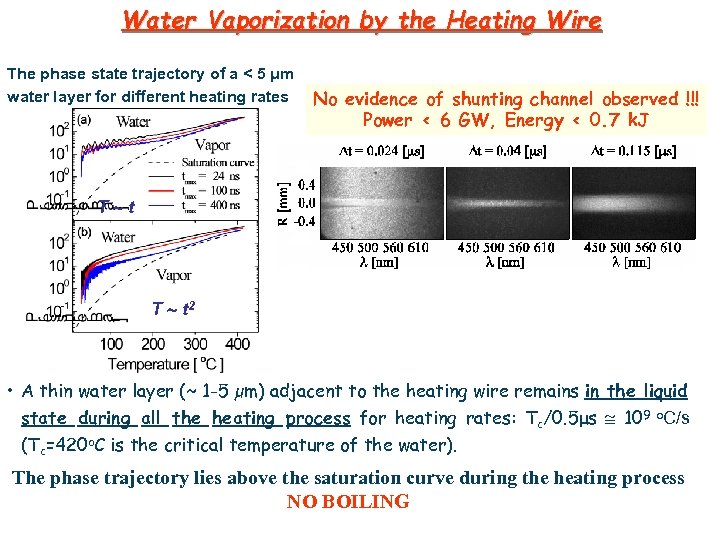Water Vaporization by the Heating Wire The phase state trajectory of a < 5 μm water layer for different heating rates No evidence of shunting channel observed !!! Power < 6 GW, Energy < 0. 7 k. J T t T t 2 • A thin water layer (~ 1 -5 µm) adjacent to the heating wire remains in the liquid state during all the heating process for heating rates: Tc/0. 5μs 109 o. C/s (Tc=420 o. C is the critical temperature of the water). The phase trajectory lies above the saturation curve during the heating process NO BOILING

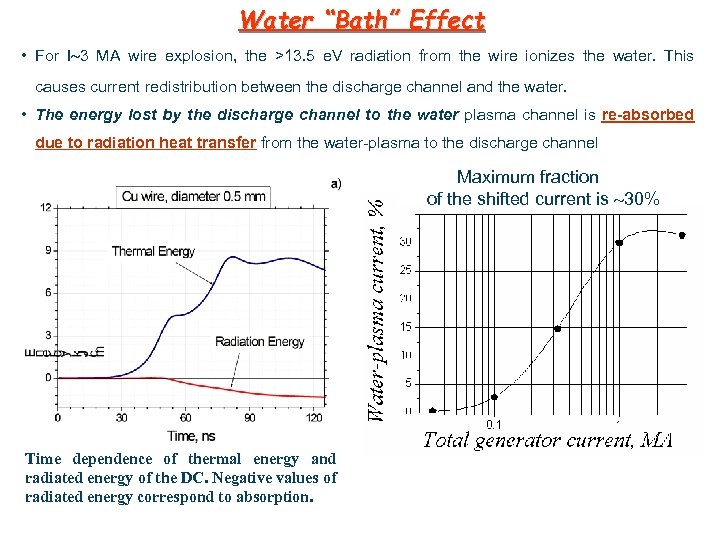Water “Bath” Effect • For I 3 MA wire explosion, the >13. 5 e. V radiation from the wire ionizes the water. This causes current redistribution between the discharge channel and the water. • The energy lost by the discharge channel to the water plasma channel is re-absorbed due to radiation heat transfer from the water-plasma to the discharge channel Maximum fraction of the shifted current is 30% Time dependence of thermal energy and radiated energy of the DC. Negative values of radiated energy correspond to absorption.

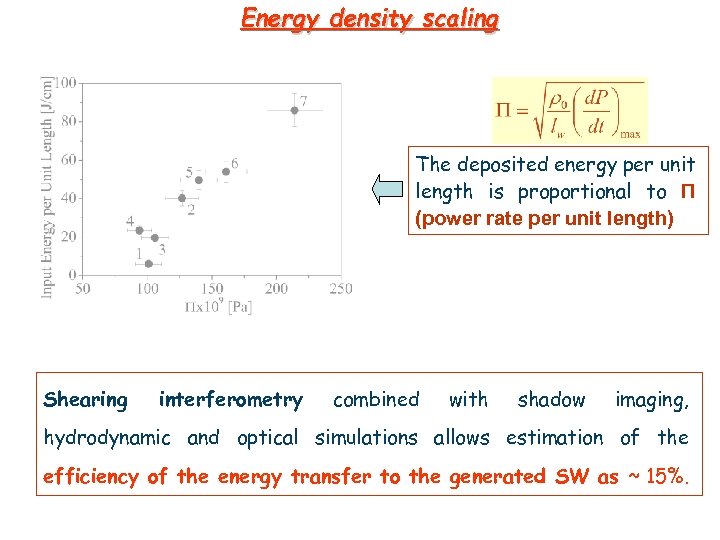Energy density scaling The deposited energy per unit length is proportional to Π (power rate per unit length) Shearing interferometry combined with shadow imaging, hydrodynamic and optical simulations allows estimation of the efficiency of the energy transfer to the generated SW as ~ 15%.

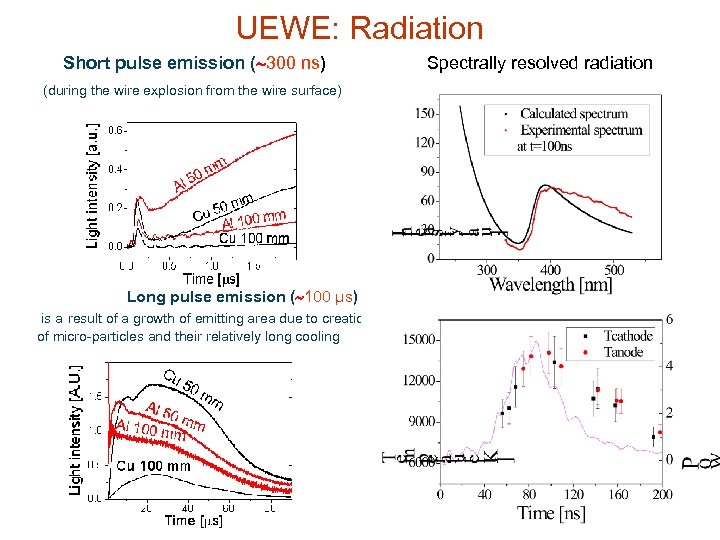UEWE: Radiation Short pulse emission ( 300 ns) (during the wire explosion from the wire surface) Long pulse emission ( 100 μs) is a result of a growth of emitting area due to creation of micro-particles and their relatively long cooling Spectrally resolved radiation

MHD Calculations Mass conservation Momentum conservation Energy conservation Maxwell equations Ohm law Equations of state Transport parameters

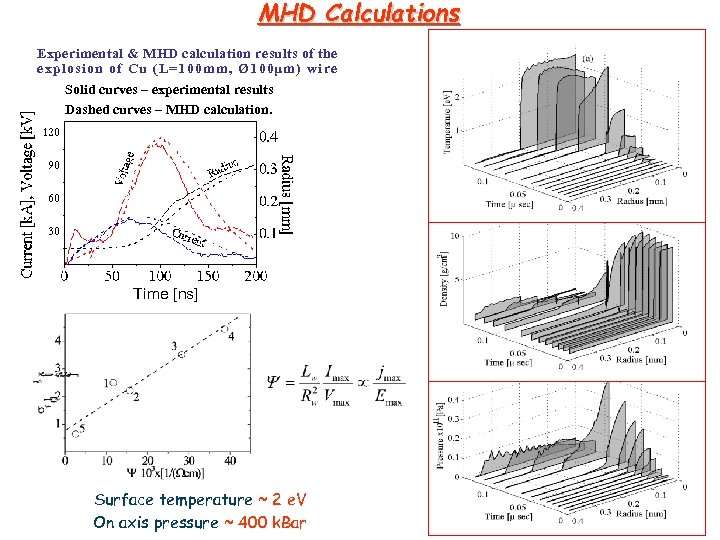MHD Calculations Experimental & MHD calculation results of the explosion of Cu (L=100 mm, Ø 100μ m) wire Solid curves – experimental results Dashed curves – MHD calculation. Time [ns] Surface temperature ~ 2 e. V On axis pressure ~ 400 k. Bar

Implosion Due to the cumulation effect of the converging SW it is possible to achieve ultra-high pressure at the axis of implosion Self-similarity problem Parametric Similarity Cylindrical Geometry R t • In the case of diverging SW (total energy of the explosion is conserved in the volume limited by the SW) the parameter can be determined using dimensional analysis of physical parameters • In the case of implosion the energy in the volume between the SW and the exploding liner is not conserved: thus cannot be determined without h y d r o - d y n a m i c n u m e r i c a l s i m u l a t i o n s. Initial energy α ~ 0. 6 - spherical implosion α ~ 0. 75 - cylindrical implosion Initial radius A. Grinenko, V. Gurovich, Ya. Krasik, Phys. Plasmas 14, 012701 (2007). V. Gurovich, A. Grinenko, Ya. Krasik, PRL 99, 124503 (2007).

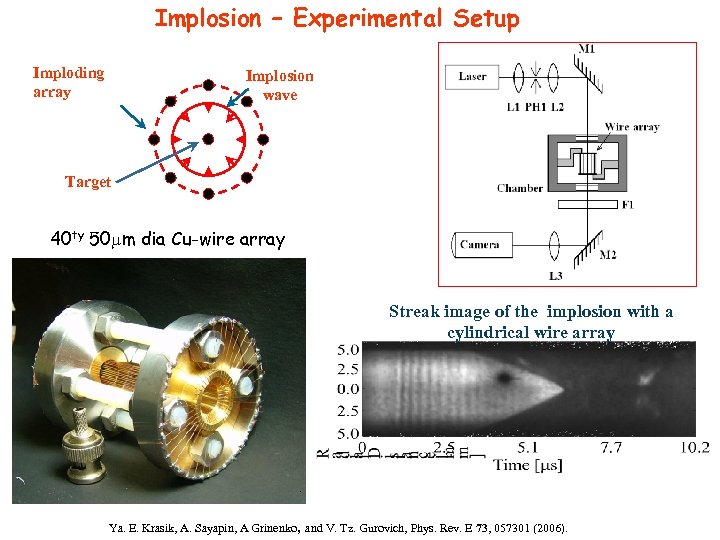Implosion – Experimental Setup Imploding array Implosion wave Target 40 ty 50 m dia Cu-wire array Streak image of the implosion with a cylindrical wire array Ya. E. Krasik, A. Sayapin, A Grinenko, and V. Tz. Gurovich, Phys. Rev. E 73, 057301 (2006).

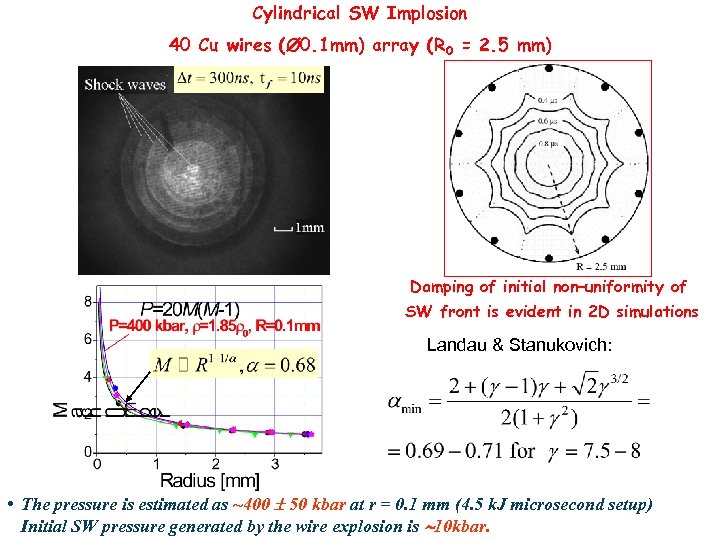Cylindrical SW Implosion 40 Cu wires (Ø 0. 1 mm) array (R 0 = 2. 5 mm) Damping of initial non–uniformity of SW front is evident in 2 D simulations Landau & Stanukovich: • The pressure is estimated as ~400 50 kbar at r = 0. 1 mm (4. 5 k. J microsecond setup) Initial SW pressure generated by the wire explosion is 10 kbar.

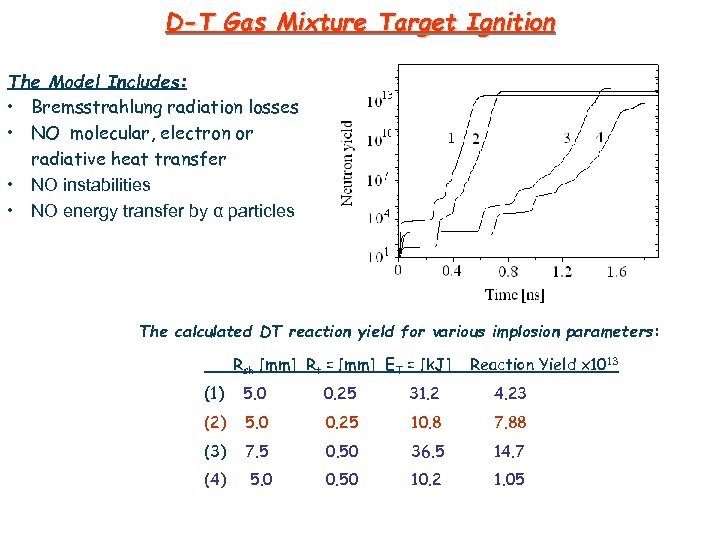D-T Gas Mixture Target Ignition The Model Includes: • Bremsstrahlung radiation losses • NO molecular, electron or radiative heat transfer • NO instabilities • NO energy transfer by α particles The calculated DT reaction yield for various implosion parameters: Rsh [mm] Rt = [mm] ET = [k. J] Reaction Yield x 1013 (1) 5. 0 0. 25 31. 2 4. 23 (2) 5. 0 0. 25 10. 8 7. 88 (3) 7. 5 0. 50 36. 5 14. 7 (4) 5. 0 0. 50 10. 2 1. 05