Public key cryptography RSA Algorithm Diffie-Hellman key exchange

Public-Key Cryptography • traditional private/secret/single key cryptography uses one key • Key is shared by both sender and receiver • if the key is disclosed communications are compromised • also known as symmetric, both parties are equal – hence does not protect sender from receiver forging a message & claiming is sent by sender

Disadvantages of Classical Cryptography • Requires secure transmission of key value • Requires a separate key for each group of people that wishes to exchange encrypted messages (readable by any group member) • For example, to have a separate key for each pair of people, 100 people would need 4950 different keys. • Cumbersome Handshaking involved in KDC

Public-Key Cryptography • probably most significant advance in the 3000 year history of cryptography • uses two keys – a public key and a private key • asymmetric since parties are not equal • uses clever application of number theory concepts to function • complements rather than replaces private key cryptography

Why Public-Key Cryptography? • developed to address two key issues: – key distribution – how to have secure communications in general without having to trust a KDC with your key – digital signatures – how to verify a message comes intact from the claimed sender • public invention due to Whitfield Diffie & Martin Hellman at Stanford U. in 1976

• Key Distribution requires that – Two communicants already share a key, which somehow has been distributed to them – Use of a key distribution center • Electronic messages and documents would need the equivalent of signatures used in paper documents.

Public-Key Cryptography • public-key/two-key/asymmetric cryptography involves the use of two keys: – a public-key, which may be known by anybody, and can be used to encrypt messages, and verify signatures – a private-key, known only to the recipient, used to decrypt messages, and sign (create) signatures • is asymmetric because – those who encrypt messages or verify signatures cannot decrypt messages or create signatures

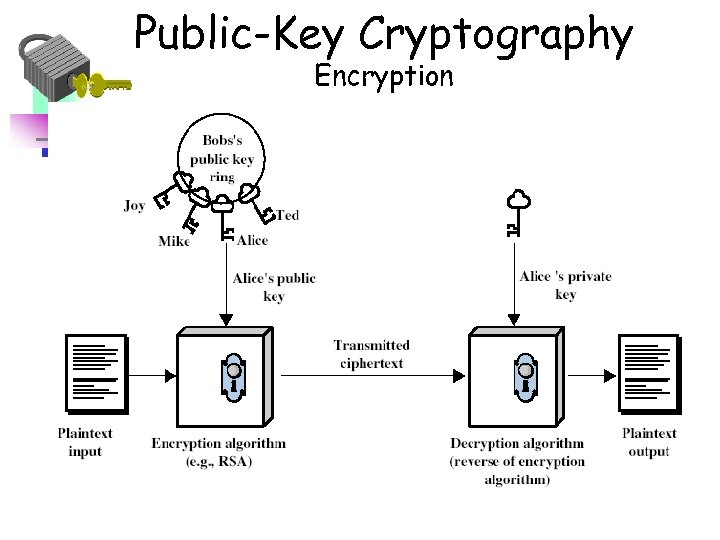
Public-Key Cryptography Encryption

• Alice generates a key value (usually a number or pair of related numbers) which she makes public. • Alice uses her public key (and some additional information) to determine a second key (her private key). • Alice keeps her private key (and the additional information she used to construct it) secret.

• Bob (or Carol, or anyone else) can use Alice’s public key to encrypt a message for Alice. • Alice can use her private key to decrypt this message. • No-one without access to Alice’s private key (or the information used to construct it) can easily decrypt the message

An Example: Internet Commerce • Bob wants to use his credit card to buy some books from Alice over the Internet. • Alice sends her public key to Bob. • Bob uses this key to encrypt his credit -card number and sends the encrypted number to Alice. • Alice uses her private key to decrypt this message (and get Bob’s creditcard number).

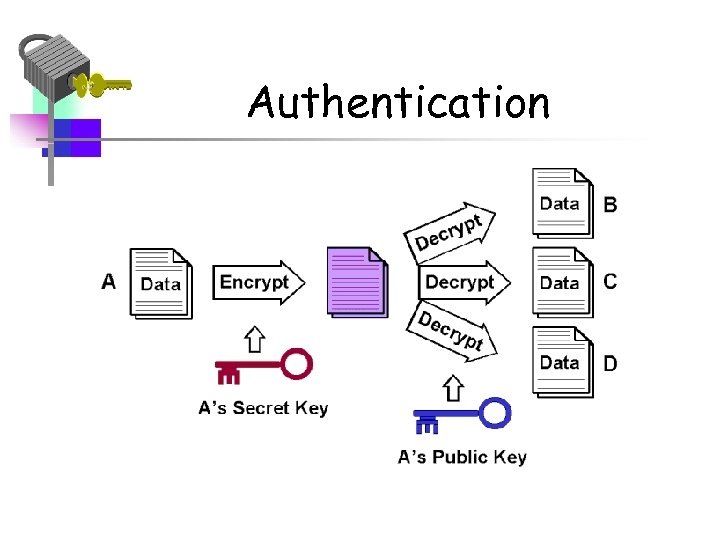
Authentication

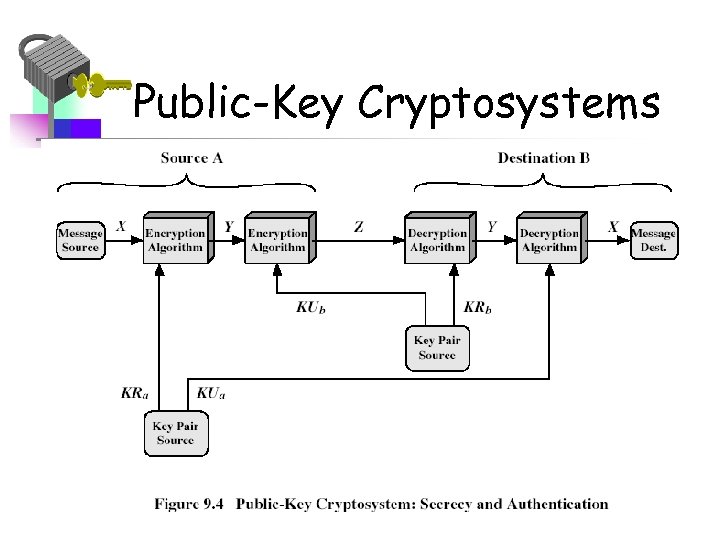
Public-Key Cryptosystems

Public-Key Applications • can classify uses into 3 categories: – encryption/decryption (provide secrecy) – digital signatures (provide authentication) – key exchange (of session keys) • some algorithms are suitable for all uses, others are specific to one

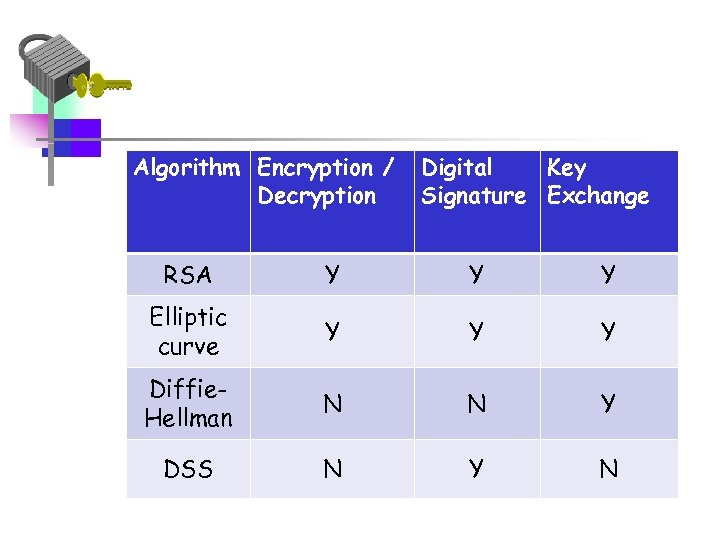
Algorithm Encryption / Decryption Digital Key Signature Exchange RSA Y Y Y Elliptic curve Y Y Y Diffie. Hellman N N Y DSS N Y N

THE RSA ALGORITHM • Public key algorithm invented in 1977 by Ron Rivest, Adi Shamir & Leonard Adleman of MIT • Best known & widely used public-key scheme • Supports Encryption & Digital signatures • Gets its security from integer factorization problem

Key Generation 1. Generate two large random primes, p and q, of approximately equal size such that their product n = pq is of the required bit length, e. g. 1024 bits. 2. Compute n = pq and phi φ(n) = (p-1)(q-1). 3. Choose an integer e, 1 < e < φ(n), such that gcd(e, φ) = 1. 4. Compute the secret exponent d, 1 < d < φ(n), such that ed ≡ 1 mod φ(n). 5. The public key is (n, e) and the private key is (n, d). Keep all the values d, p, q and φ(n) secret. • n is known as the modulus. • e is known as the public exponent or encryption exponent or just the exponent. • d is known as the secret exponent or decryption exponent.

Key Generation -detail 1. Use a random process to select two large prime numbers p and q. Compute the product n = p*q. This number is called the modulus, and is made publicly available. – RSA currently recommends a modulus that’s at least 768 bits long. 2. Also compute the Euler totient φ(n) = φ(pq)= (p-1)*(q-1). Keep this number (as well as p and q) secret.

GCD & Relatively prime • Two numbers a and b which have no common factors other than one are said to be coprime or relatively prime. For example, 4 and 9 are coprime but 15 and 25 are not. • The greatest common divisor of two integers a and b is the largest integer that divides both numbers and is denoted by ‘gcd(a, b)’. For example, gcd(25, 15) = 5 and gcd(4, 9) = 1. • a and b are coprime if and only if gcd(a, b) = 1.

Euler Totient φ(n) is the no. of positive integers less than n and relatively prime to n. e. g. φ(12)=4 as the four integers {1, 5, 7, 11} are coprime to 12. φ(7)=6 as the 6 integers {1, 2, 3, 4, 5, 6} are coprime to 7. i. e. for any prime p, φ(p) = p-1

Key Generation -detail 3. Randomly choose a public key e that has no factors in common with φ(n)= (p -1)*(q-1). so that gcd(e, φ(n)) = 1, 1 < e < φ(n); [Euclid’s algorithm: gcd(a, b)=gcd(b, r) where r=a mod b e. g. gcd(18, 12)=gcd(12, 6)=gcd(6, 0)=6 i. e. a = qb + r] 4. Solve following equation to find decryption key d , e. d ≡ 1 mod φ(n) and d < n; where d is the multiplicative inverse of e in mod φ(n); d ≡ e-1 mod φ(n)

• ‘mod’ as a congruence relation: The • • notation ‘a ≡ b (mod n)’ means a and b have the same remainder when divided by n, or, equivalently, (a) n|a − b, or (b) a − b = nk for some integer k. We say that a is congruent to b modulo n, where n is the modulus of the congruence. The two ways of using ‘mod’ are related: a ≡ b (mod n) <==> a mod n = b mod n.

• Compute a private key d so that e*d leaves a remainder of 1 when divided by φ(n). Find a value for d such that φ(n) divides (ed-1). Note that d is easy to compute only if one knows the value of φ(n). This is essentially the same as knowing the values of p and q.

Using RSA • publish their public encryption key: KU={e, n} • keep secret private decryption key: KR={d, p, q} • to encrypt a message M the sender: – obtains public key of recipient KU={e, n} – computes: C=Me mod n, where 0≤M<n • to decrypt the ciphertext C the owner: – uses their private key KR={d, p, q} – computes: M=Cd mod n

RSA Example 1. 2. 3. 4. 5. Select primes: p =17 & q =11 Compute n = pq =17× 11=187 Compute ø(n)=(p– 1)(q-1)=16× 10=160 Select e : gcd(e, 160)=1; choose e =7 Determine d: de=1 mod 160 and d < 160 Value is d=23 since 23× 7=161= 1× 160+1 6. Publish public key KU={7, 187} 7. Keep secret private key KR={23, 17, 11}

• Use a property of modular arithmetic: (a x b) mod n = [ (a mod n) x (b mod n) ] mod n • modulo of a product = modulo of the product of its multipliers’ modulos • Strategy - reduce xy into xaxbxc where y=abc using powers of 2 for a, b, c. Then apply above property

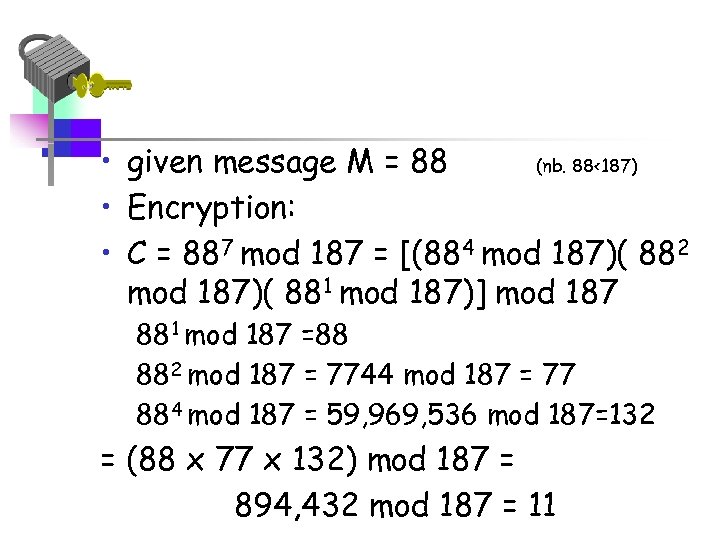
• given message M = 88 (nb. 88<187) • Encryption: • C = 887 mod 187 = [(884 mod 187)( 882 mod 187)( 881 mod 187)] mod 187 881 mod 187 =88 882 mod 187 = 7744 mod 187 = 77 884 mod 187 = 59, 969, 536 mod 187=132 = (88 x 77 x 132) mod 187 = 894, 432 mod 187 = 11

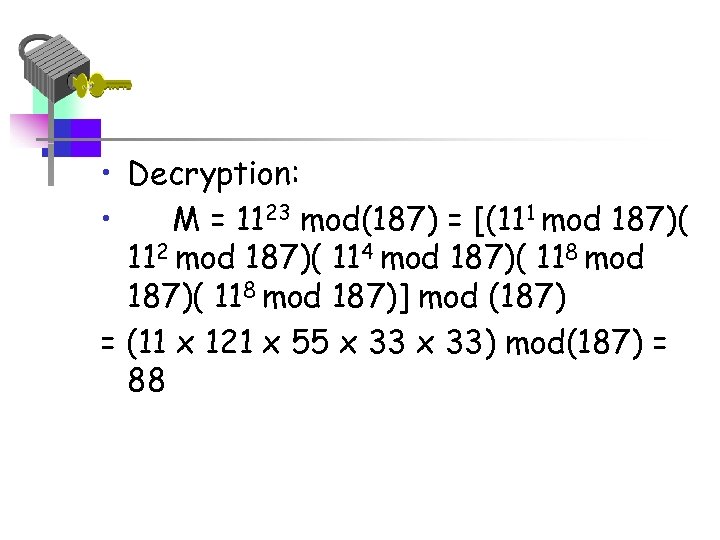
• Decryption: • M = 1123 mod(187) = [(111 mod 187)( 112 mod 187)( 114 mod 187)( 118 mod 187)] mod (187) = (11 x 121 x 55 x 33) mod(187) = 88

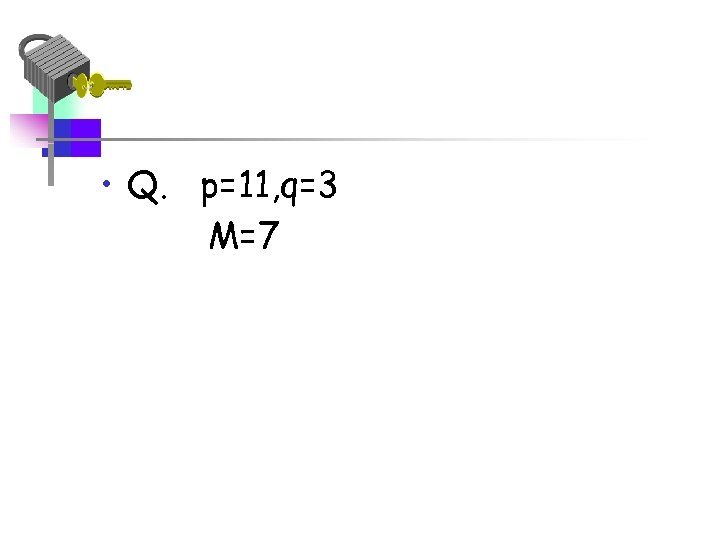
• Q. p=11, q=3 M=7

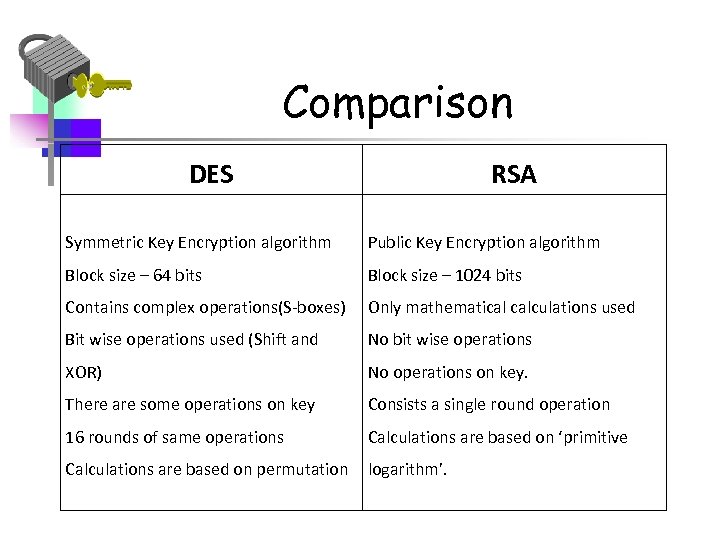
Comparison DES RSA Symmetric Key Encryption algorithm Public Key Encryption algorithm Block size – 64 bits Block size – 1024 bits Contains complex operations(S-boxes) Only mathematical calculations used Bit wise operations used (Shift and No bit wise operations XOR) No operations on key. There are some operations on key Consists a single round operation 16 rounds of same operations Calculations are based on ‘primitive Calculations are based on permutation logarithm’.

Diffie-Hellman Key Exchange • Whittfield Diffie and Martin Hellman are called the inventors of Public Key Cryptography. • Diffie-Hellman Key Exchange is the first Public Key Algorithm published in 1976.

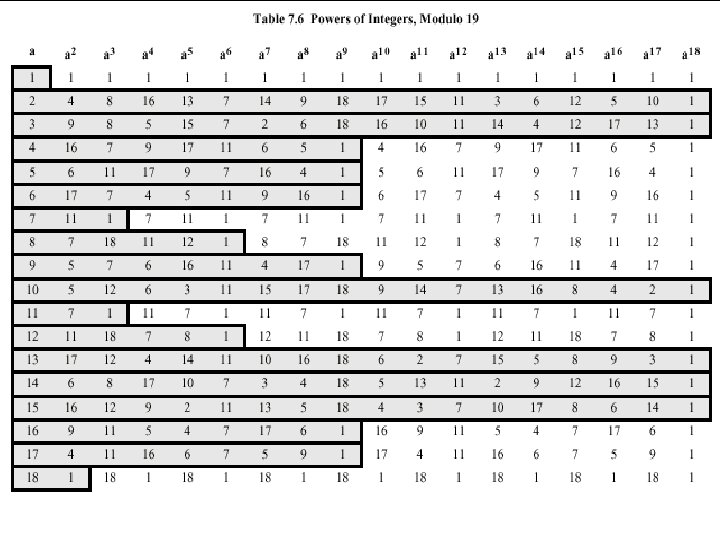
Discrete Logarithms • • What is a logarithm? log 10100 = 2 because 102 = 100 In general if logmb = a then ma = b Where m is called the base of the logarithm • A discrete logarithm can be defined for integers only • In fact we can define discrete logarithms mod p also where p is any prime number

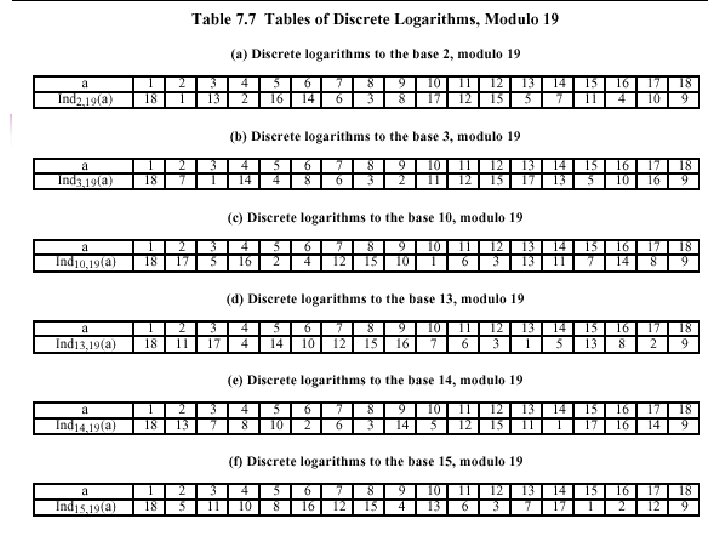
Primitive Roots • If x n = a then a is called the n-th root of x • For any prime number p, if we have a number a such that powers of a mod p generate all the numbers between 1 to p-1 then a is called a Primitive Root of p. • Then for any integer b and a primitive root a of prime number p we can find a unique exponent i such that b = a i mod p • The exponent i is referred to as the discrete logarithm or index, of b for the base a.

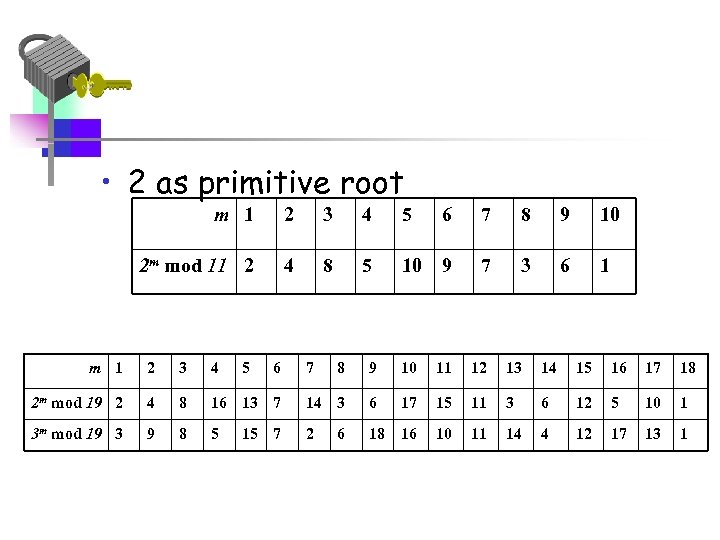
• 2 as primitive root m 1 2 3 4 5 6 7 8 9 10 2 m mod 11 2 4 8 5 10 9 7 3 6 1 m 1 2 3 4 2 m mod 19 2 4 8 3 m mod 19 3 9 8 5 6 8 9 10 11 12 13 14 15 16 17 18 16 13 7 14 3 6 17 15 11 3 6 12 5 10 1 5 2 18 16 10 11 14 4 12 17 13 1 15 7 7 6

Diffie-Hellman Algorithm • Five Parts 1. 2. 3. 4. 5. Global Public Elements User A Key Generation User B Key Generation of Secret Key by User A Generation of Secret Key by User B

Global Public Elements • p Prime number • g g < p and g is a primitive root of p • The global public elements are also sometimes called the domain parameters

User A Key Generation • Select private XA • Calculate public YA XA < p YA = g XA mod p

User B Key Generation • Select private XB • Calculate public YB XB < p YB = g XB mod p

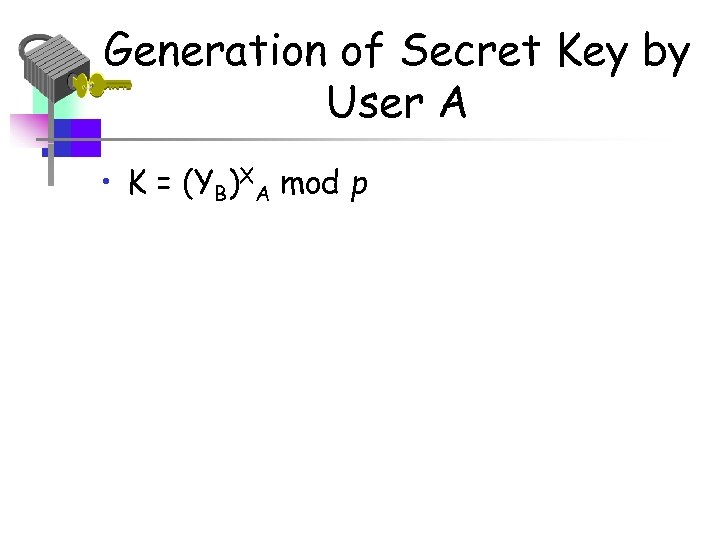
Generation of Secret Key by User A • K = (YB)XA mod p

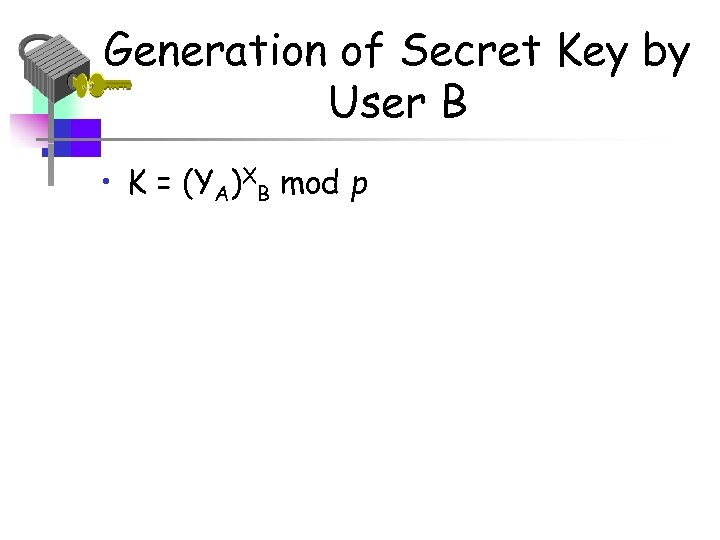
Generation of Secret Key by User B • K = (YA)XB mod p

Diffie-Hellman Key Exchange • Alice and Bob agree upon and make public two • numbers g and p, where p is a prime and g is a primitive root mod p. Note: Anyone has access to these numbers. • The Exchange: 1. Alice chooses a random number a (secret)and computes u =g a (mod p), and sends u to Bob. 2. Bob chooses a random number b (secret) and computes v= g b (mod p), and sends v to Alice. 3. Bob computes the key kb using secret b= u b mod p 4. Alice computes the key ka using secret a=v a mod p Now, both Alice and Bob have the same key, namely ka = kb = gab (mod p).

• kb = u b mod p =(g a mod p)b mod p =(g a)b mod p by modular arithmetic = g ab mod p =(g b)a mod p =(g b mod p)a mod p = v a mod p = ka

Example • Suppose Alice and Bob agree to • use p = 47 and g = 5. • Alice chooses a number between 0 and 46, • say a = 18. • Bob chooses a number between 0 and 46, • say b = 22.

Example • • • Alice publishes ga (mod p), i. e. u = 518 (mod 47) = 2. Bob publishes gb (mod p), i. e. v = 522 (mod 47) = 28. If Alice wants to know the secret key k, she takes Bob’s public number, v =28 and raises it to her private number, a = 18 (taking the result mod 47). • This gives her: 2818 (mod 47) = 24.

Example • If Bob wants to know the secret key, he takes Alice’s public number, u = 2, and raises it to his private number, b = 22 (taking the result mod 47). • This gives him: 222 (mod 47) = 24. • Thus, Alice and Bob have agreed upon a secret key, k = 24.

Security of DH exchange • Opponent Eve has the following ingredients p, g, u, v to work with • If Eve wants to compute k, then she would need either a or b. • Otherwise, Eve would need to solve a Discrete Logarithm Problem. – There is no known algorithm to accomplish this in a reasonable amount of time. – E. g. for attacking user B’s secret key, the opponent must compute b=indg, p(v)

Man in the middle attack • Susceptibility: If Eve can intercept u and v, it is possible for her to substitute her own u’ and v’. • If she can intercept all communication • between Alice and Bob, then she can substitute her own messages. • In 1992, the exchange was modified to prevent the man-in-the-middle attack described above.

Example for m-i-t-m-a • Alice wants to talk to Bob, sends her public key to Bob. • But Eve intercepts it, and replaces Alice’s public key with hers. She sends this to Bob. • Bob thinks Alice wants to talk to him. He sends his public key to her. • But Eve intercepts and replaces! • Then Eve sets up shared keys with both!

What to do? • If the public keys are certified (e. g. , Veri. Sign) then Alice and Bob verifies that they got the right public keys!

• User Authentication: Alice encrypts the message, m, with her private key a, call it ma. ma = Ea (m) • Alice encrypts ma with Bob’s public key, v, and sends the message to Bob. ma v = Ev (ma) • Bob recovers ma using his private key b and recovers m by using Alice’s public key u. m = Du(Db(mav)) • Thus, Bob is sure that only Alice could have sent the message.