51ae165feb639f85e7107e1d304041f4.ppt
- Количество слайдов: 55

• Public-Key Cryptography and Message Authentication Henric Johnson Blekinge Institute of Technology, Sweden http: //www. its. bth. se/staff/hjo/ henric. johnson@bth. se 1

OUTLINE • Approaches to Message Authentication • Secure Hash Functions • Digital Signatures 2

Message Authentication • message authentication is concerned with: – protecting the integrity of a message – validating identity of originator – non-repudiation of origin (dispute resolution) • will consider the security requirements • then three alternative functions used: – message encryption – message authentication code (MAC) – hash function 3

Security Requirements • • disclosure traffic analysis masquerade content modification sequence modification timing modification source repudiation destination repudiation 4

Message Encryption • message encryption by itself also provides a measure of authentication • if symmetric encryption is used then: – receiver knows that the sender must have created the message – since only sender and receiver know key used, content of the message cannot have been altered – if message has a suitable structure, redundancy or a checksum to detect any changes 5

Message Encryption • if public-key encryption is used: – encryption provides no confidence of sender – since anyone potentially knows public-key – however if • sender signs message using their private-key • then encrypts with recipients public key • have both secrecy and authentication – again need to recognize corrupted messages – but at cost of two public-key uses on message 6

Message Authentication Code (MAC) • generated by an algorithm that creates a small fixed-sized block – depending on both message and some key – like encryption though need not be reversible • appended to message as a signature • receiver performs same computation on message and checks it whether matches the MAC • provides assurance that message is unaltered and comes from sender 7
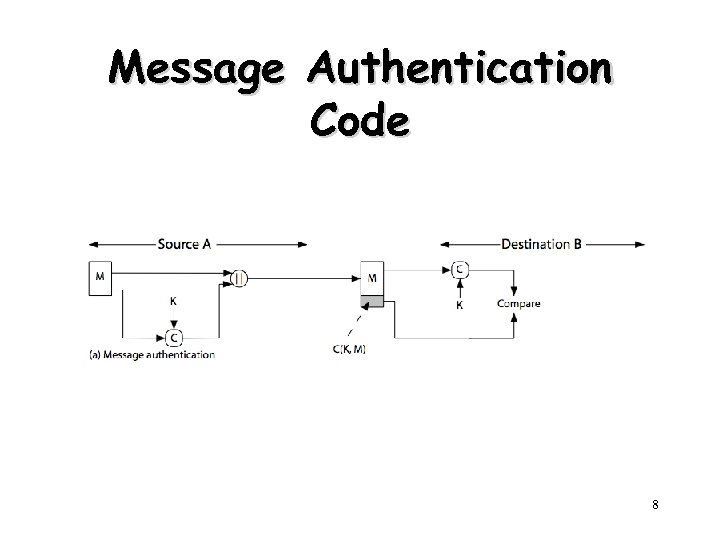
Message Authentication Code 8

Message Authentication Codes • as shown the MAC provides authentication • can also use encryption for secrecy – generally use separate keys for each – can compute MAC either before or after encryption – is generally regarded as better done before • why use a MAC? – sometimes only authentication is needed – sometimes need authentication to persist longer than the encryption (eg. archival use) • note that a MAC is not a digital signature 9

Authentication • Requirements - must be able to verify that: 1. Message came from apparent source or author, 2. Contents have not been altered, 3. Sometimes, it was sent at a certain time or sequence. • Protection against active attack (falsification of data and transactions) 10

Approaches to Message uthentication • Authentication Using Conventional Encryption – Only the sender and receiver should share a key • Hash Function: Message digest function – An authentication tag (fingerprint) is generated and appended to each message • Message Authentication Code – Calculate the MAC as a function of the message and the shared secret key. MAC = F(K, M) = Cryptographic cheksum 11
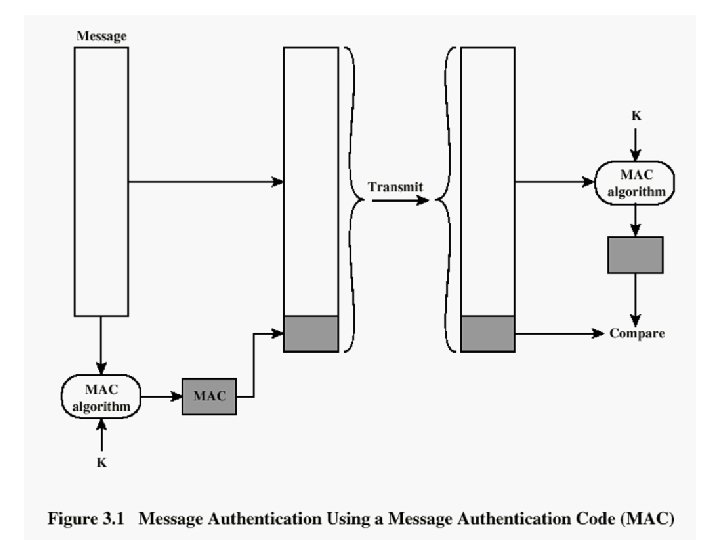
12
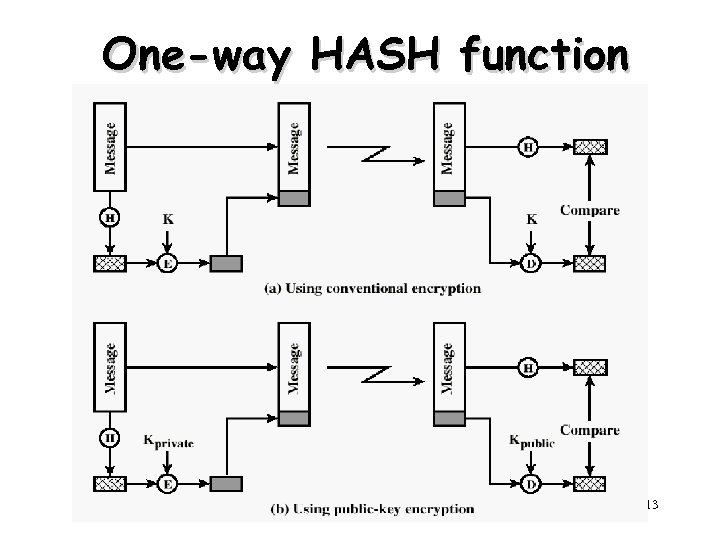
One-way HASH function 13
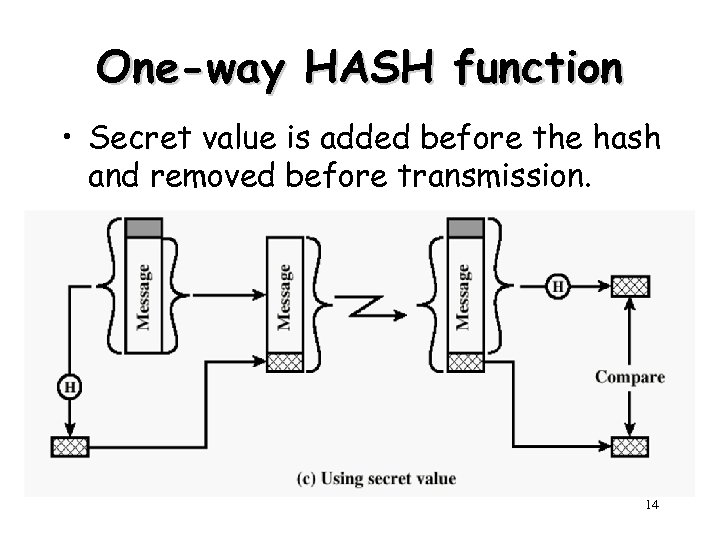
One-way HASH function • Secret value is added before the hash and removed before transmission. 14

Using Symmetric Ciphers for MACs • can use any block cipher chaining (CBC) mode and use final block as a MAC • Data Authentication Algorithm (DAA) is a widely used MAC based on DES-CBC – using IV=0 and zero-pad of final block – encrypt message using DES in CBC mode – and send just the final block as the MAC • or the leftmost M bits (16≤M≤ 64) of final block • but final MAC is now too small for security 15

MAC Based on DES D 1, D 2, D 3, . . . , DN = 64 bits Data blocks E = DES Encryption Algorithm, K = Secret key Q 1 = E(K, D 1) Q 2 = E(K, [D 2^Q 1]) Q 3 = E(K, [D 3^Q 2]). . . QN = E(K, [DN^QN-1]) 16
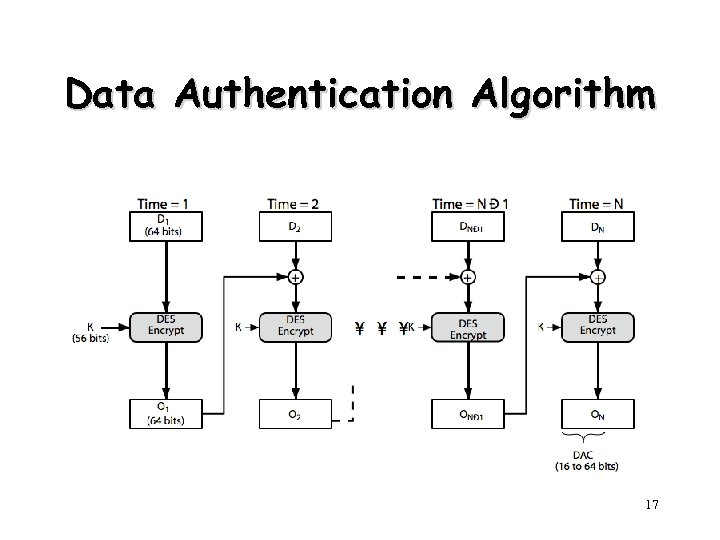
Data Authentication Algorithm 17

Secure HASH Functions • • Purpose of the HASH function is to produce a ”fingerprint. Properties of a HASH function H : 1. 2. 3. 4. H can be applied to a block of data of any size H produces a fixed length output H(x) is easy to compute for any given x. For any given block x, it is computationally infeasible to find x such that H(x) = h 5. For any given block x, it is computationally infeasible to find with H(y) = H(x). 6. It is computationally infeasible to find any pair (x, y) such that H(x) = H(y) 18
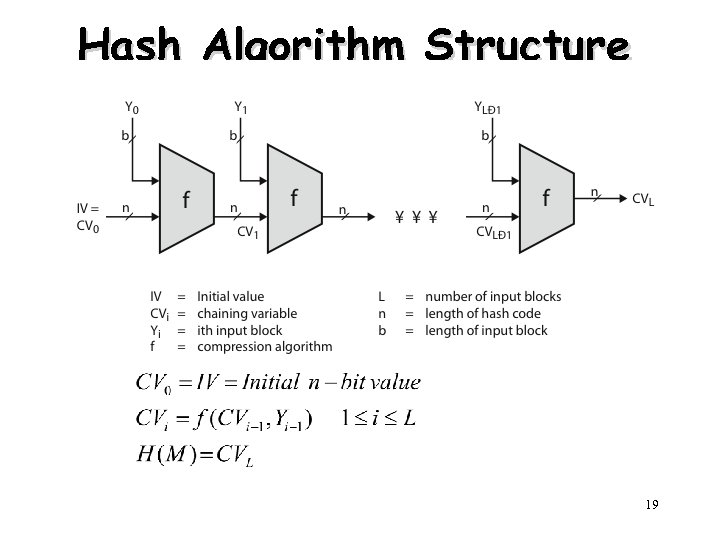
Hash Algorithm Structure 19

Secure Hash Algorithm • SHA originally designed by NIST & NSA in 1993 • was revised in 1995 as SHA-1 • US standard for use with DSA signature scheme – standard is FIPS 180 -1 1995, also Internet RFC 3174 – nb. the algorithm is SHA, the standard is SHS • based on design of MD 4 with key differences • produces 160 -bit hash values • recent 2005 results on security of SHA-1 have raised concerns on its use in future applications 20

Revised Secure Hash Standard • NIST issued revision FIPS 180 -2 in 2002 • adds 3 additional versions of SHA – SHA-256, SHA-384, SHA-512 • designed for compatibility with increased security provided by the AES cipher • structure & detail is similar to SHA-1 • hence analysis should be similar • but security levels are rather higher 21
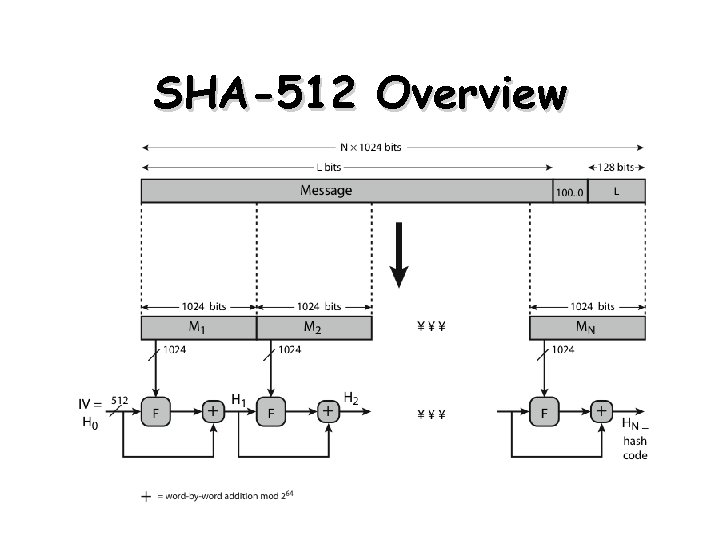
SHA-512 Overview 22

SHA-512 Compression Function • heart of the algorithm • processing message in 1024 -bit blocks • consists of 80 rounds – updating a 512 -bit buffer – using a 64 -bit value Wt derived from the current message block – and a round constant based on cube root of first 80 prime numbers 23
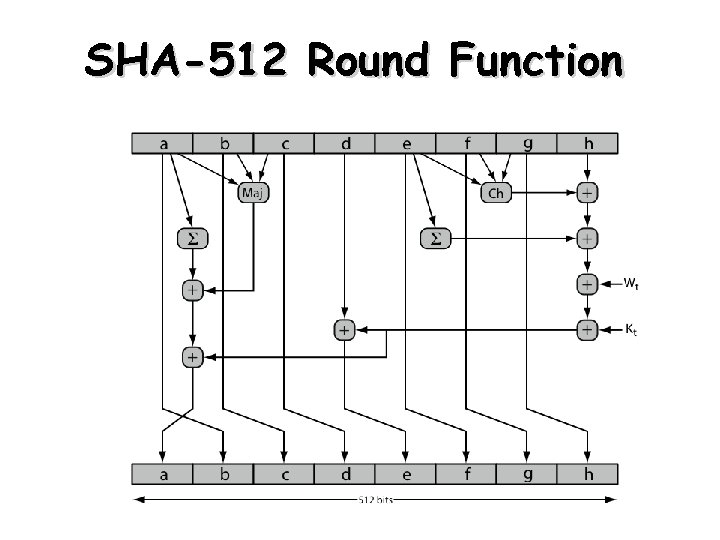
SHA-512 Round Function 24
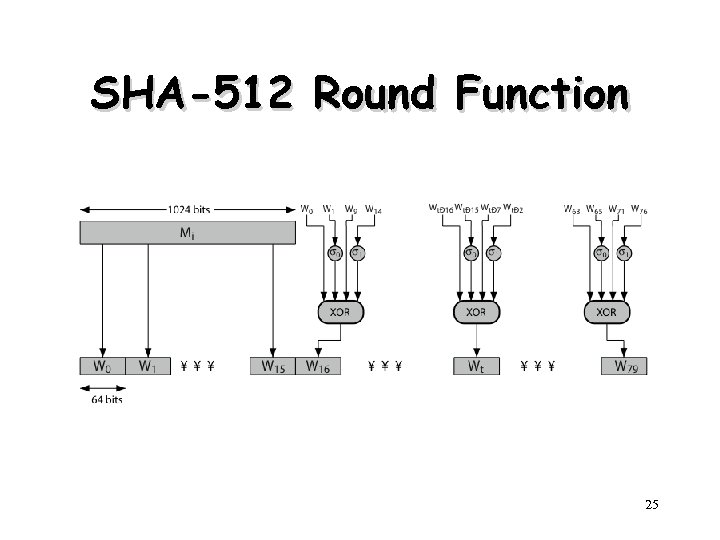
SHA-512 Round Function 25
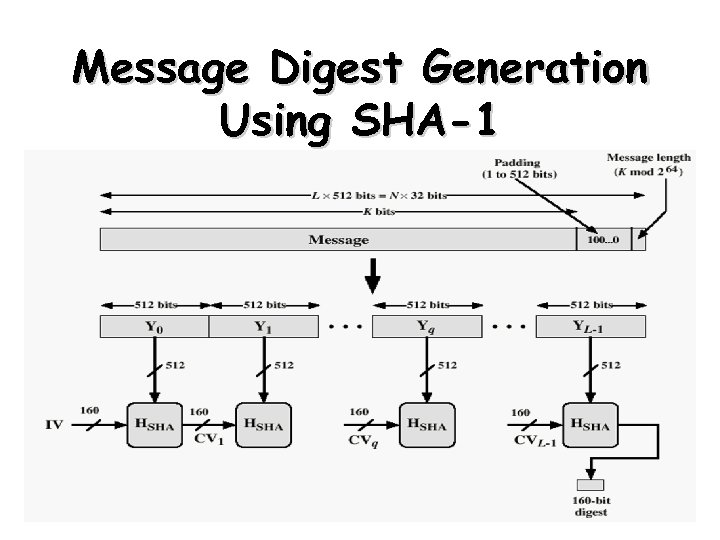
Message Digest Generation Using SHA-1 26
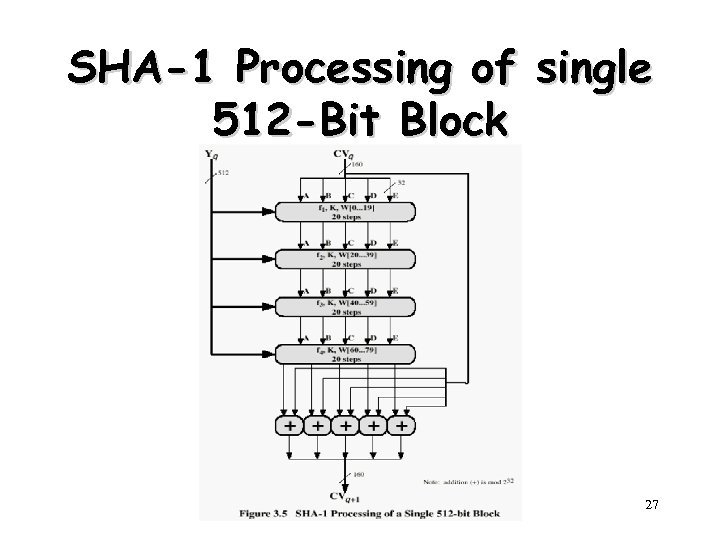
SHA-1 Processing of single 512 -Bit Block 27

Other Secure HASH functions SHA-1 MD 5 RIPEMD-160 Digest length 160 bits 128 bits 160 bits Basic unit of processing 512 bits 64 (4 rounds of 16) 160 (5 paired rounds of 16) Number of steps 80 (4 rounds of 20) Maximum message size 264 -1 bits 28

HMAC • Uses a MAC derived from a cryptographic hash code, such as SHA-1. • Motivations: – Cryptographic hash functions executes faster in software than encryptoin algorithms such as DES – Library code for cryptographic hash functions is widely available – No export restrictions from the US 29

HMAC Algorithm H = Embedded H function (e. g. , MD 5, SHA-1, RIPEMD-160) IV = Initial Value, input to hash function M = Message input including padding Yi = ith block of M, L = Number of blocks in M b = Number of bits in a block n = Length of hash code produced by embedded hash function K = Secret key K+ = Key padded with zeros on the left so that the result is b bits ipad = 00110110 (36 Hexadecimal) repeated b/8 times opad = 01011100 (5 CHexadecimal) repeated b/8 times 30

HMAC Algorithm 1. Append zeros to the left end of K to create a b-bit string K+ 2. XOR K+ with ipad to produce the b-bit blocks Si 3. Append M to Si 4. Apply H to the stream generated in step 3 5. XOR K+ with opad to produce the b-bit blocks So 6. Append the hash result from step 4 to So 7. Apply H to the stream generated in step 6 and output the result 31
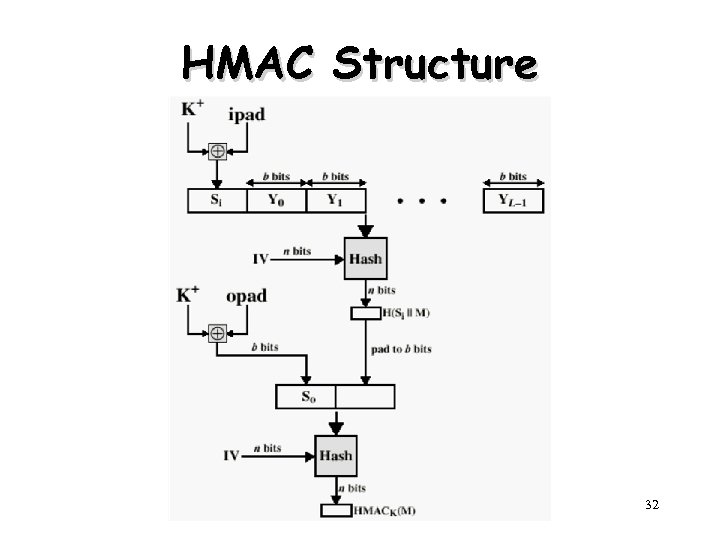
HMAC Structure 32

Public Key Cryptography and RSA

Private-Key Cryptography Ø traditional private/secret/single key cryptography uses one key Ø shared by both sender and receiver Ø if this key is disclosed communications are compromised Ø also is symmetric, parties are equal Ø hence does not protect sender from receiver forging a message & claiming is sent by sender

Public-Key Cryptography • probably most significant advance in the 3000 year history of cryptography • uses two keys – a public & a private key • asymmetric since parties are not equal • uses clever application of number theoretic concepts to function • complements rather than replaces private key crypto

Why Public-Key Cryptography? • developed to address two key issues: – key distribution – how to have secure communications in general without having to trust a KDC with your key – digital signatures – how to verify a message comes intact from the claimed sender • public invention due to Whitfield Diffie & Martin Hellman at Stanford Uni in 1976 – known earlier in classified community

Public-Key Cryptography • public-key/two-key/asymmetric cryptography involves the use of two keys: – a public-key, which may be known by anybody, and can be used to encrypt messages, and verify signatures – a related private-key, known only to the recipient, used to decrypt messages, and sign (create) signatures • infeasible to determine private key from public • is asymmetric because – those who encrypt messages or verify signatures cannot decrypt messages or create signatures
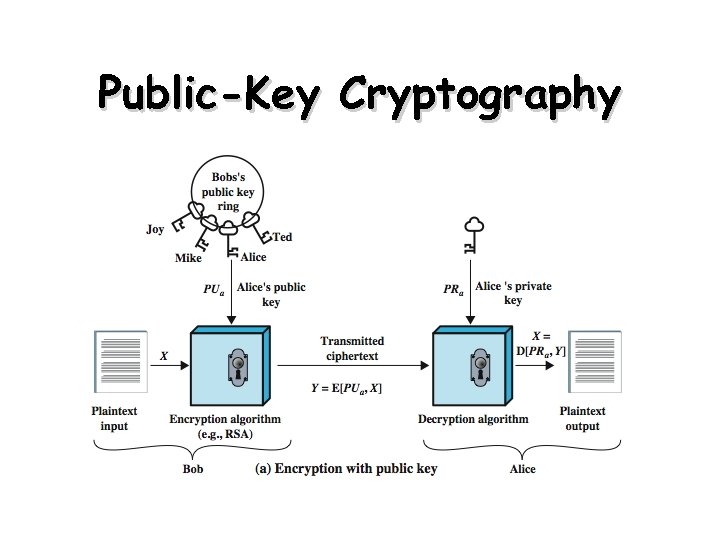
Public-Key Cryptography
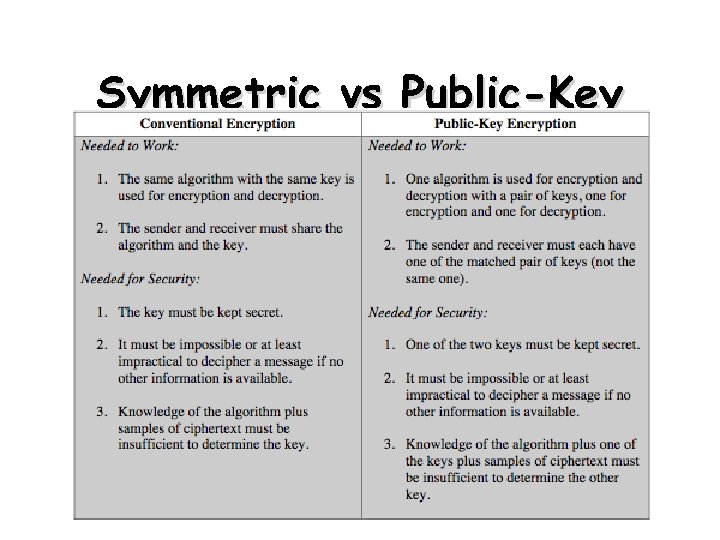
Symmetric vs Public-Key

RSA Ø by Rivest, Shamir & Adleman of MIT in 1977 Ø best known & widely used public-key scheme Ø based on exponentiation in a finite (Galois) field over integers modulo a prime l nb. exponentiation takes O((log n)3) operations (easy) Ø uses large integers (eg. 1024 bits) Ø security due to cost of factoring large numbers l nb. factorization takes O(e (hard) log n) operations

RSA En/decryption • to encrypt a message M the sender: – obtains public key of recipient PU={e, n} – computes: C = Me mod n, where 0≤M<n • to decrypt the ciphertext C the owner: – uses their private key PR={d, n} – computes: M = Cd mod n • note that the message M must be smaller than the modulus n (block if needed)

Fermat’s Theorem 42

Euler’s Theorem Euler’s totient function written as (n), and defined as the number of positive integers less than n and relatively prime to n. (1)=1. For a prime number p (p)=p-1. Theorem: For every a and n that are relatively prime, we have 43

The RSA Algorithm – Key Generation 1. 2. 3. 4. 5. 6. 7. Select p, q Calculate n = p x q Calculate Select integer e Calculate d Public Key Private key p and q both prime KU = {e, n} KR = {d, n} 44
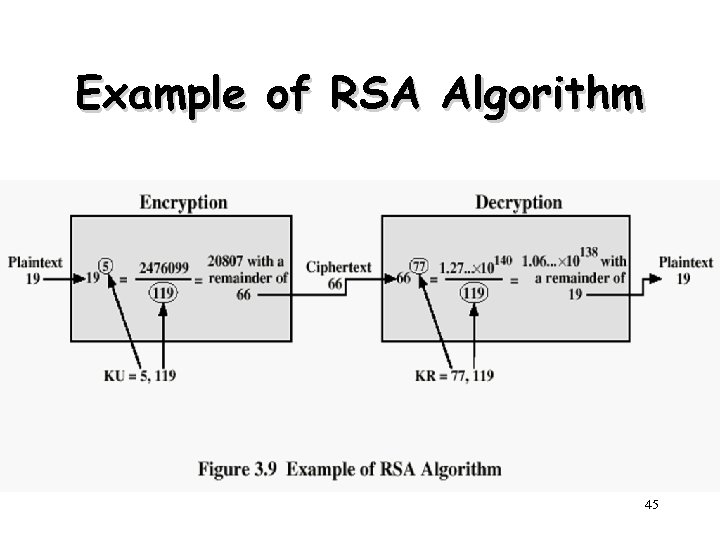
Example of RSA Algorithm 45
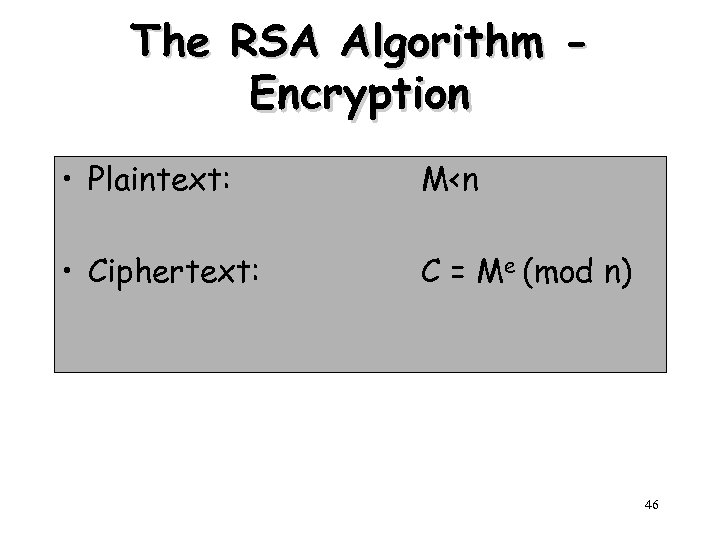
The RSA Algorithm Encryption • Plaintext: M<n • Ciphertext: C = Me (mod n) 46

The RSA Algorithm Decryption • Ciphertext: C • Plaintext: M = Cd (mod n) 47

Why RSA Works • because of Euler's Theorem: – aø(n)mod n = 1 where gcd(a, n)=1 • in RSA have: – – n=p. q ø(n)=(p-1)(q-1) carefully chose e & d to be inverses mod ø(n) hence e. d=1+k. ø(n) for some k • hence : Cd = Me. d = M 1+k. ø(n) = M 1. (Mø(n))k = M 1. (1)k = M 1 = M mod n

RSA Example - Key Setup 1. 2. 3. 4. 5. Select primes: p=17 & q=11 Calculate n = pq =17 x 11=187 Calculate ø(n)=(p– 1)(q-1)=16 x 10=160 Select e: gcd(e, 160)=1; choose e=7 Determine d: de=1 mod 160 and d < 160 Value is d=23 since 23 x 7=161= 10 x 160+1 6. Publish public key PU={7, 187} 7. Keep secret private key PR={23, 187}

RSA Example En/Decryption Ø sample RSA encryption/decryption is: Ø given message M = 88 (nb. 88<187) Ø encryption: C = 887 mod 187 = 11 Ø decryption: M = 1123 mod 187 = 88

Exponentiation • can use the Square and Multiply Algorithm • a fast, efficient algorithm for exponentiation • concept is based on repeatedly squaring base • and multiplying in the ones that are needed to compute the result • look at binary representation of exponent • only takes O(log 2 n) multiples for number n – eg. 75 = 74. 71 = 3. 7 = 10 mod 11 – eg. 3129 = 3128. 31 = 5. 3 = 4 mod 11

Exponentiation c = 0; f = 1 for i = k downto 0 do c = 2 x c f = (f x f) mod n if bi == 1 then c = c + 1 f = (f x a) mod n return f
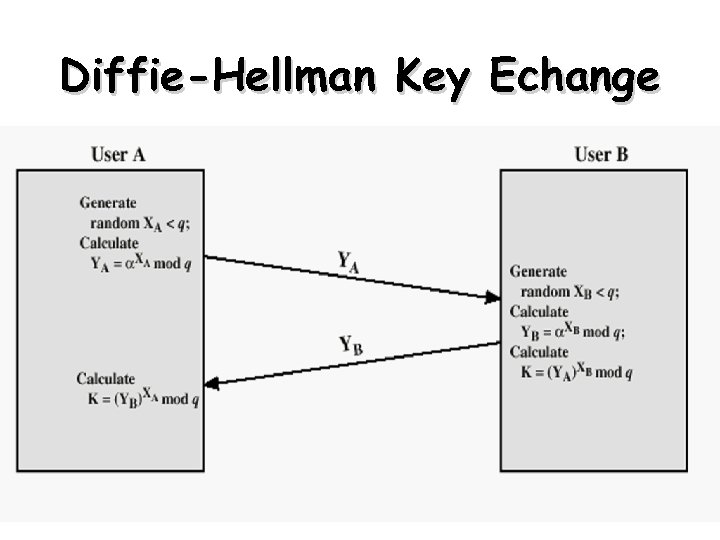
Diffie-Hellman Key Echange 53

Other Public-Key Cryptographic Algorithms • Digital Signature Standard (DSS) – Makes use of the SHA-1 – Not for encryption or key echange • Elliptic-Curve Cryptography (ECC) – Good for smaller bit size – Low confidence level, compared with RSA – Very complex 54
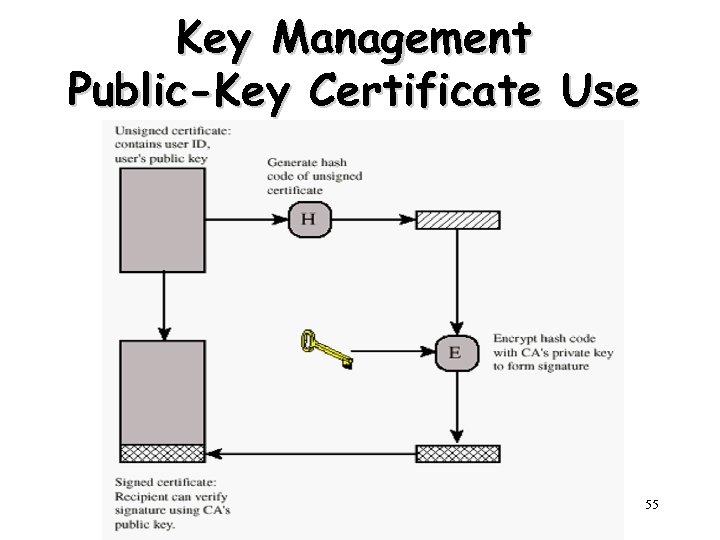
Key Management Public-Key Certificate Use 55
51ae165feb639f85e7107e1d304041f4.ppt