27b3f77042f217a8ba8c1fb0b844ec8f.ppt
- Количество слайдов: 22

Public Choice through Mobility © Allen C. Goodman, 2009

Issues with Optimal Amount • Optimal literature on choosing the amount of public goods was pretty pessimistic. • If you ask people how much they want, and you tell them they will be taxed, they will “lowball” their responses. • If they don’t think it will be related to taxes, they will “highball” their responses. • Tiebout wrote a “response” in 1956.

Tiebout Model • You have a bunch of municipalities. • Each one offers different amounts of public goods. • Consumers can’t adjust at the margin like with private goods, but. . .
Tiebout Model • They vote with their feet. • If they don’t like what’s being provided in one community, they move to another.

• Assumptions Eq’m occurs when people stop moving! – Jurisdictional Choice -Households shop for what local governments provide. – Information and Mobility -Households have perfect information, and are perfectly mobile. – No Jurisdictional Spillovers -What is produced in Southfield doesn’t affect people in Oak Park. – Community size – City manager seeks to reach average minimum cost of producing goods. – Head Taxes -- Pay for things with a tax person – all pay, no one is What happens if people keep moving subsidized. From Community 1 to Community 2? • We get an equilibrium. People’s preferences are satisfied.

Note on returns to scale • If public goods can be produced with constant returns to scale exact satisfying of preferences. • This assumption kind of assumes away part of what’s public about public goods!

Is this sensible? Fisher points out: In 1950 s and 1960 s, approx 20% of the population moved each year. Currently, it’s about 14%, but this is still over 40 million people per year. Local moves tend to be for housing related reasons. Renters move more often than homeowners.

Tiebout Model • Critique – People aren’t perfectly informed. – There may not be enough jurisdictions to meet everyone’s preferences. – Income matters. Someone from Detroit cannot move to Bloomfield Hills to take advantage of public goods in Bloomfield Hills. – Where you work matters. – It’s probably a better model for suburbs than for central cities. – Very few places have a “head tax. ”

Lots of Tiebout Literature • We have to make things more realistic. • In most places local public goods are financed by property taxes. • Property taxes are a constant percentage of the value of the property.

Rent and Value y is the annual value of housing services (the amount of rent you would pay. r is interest rate. How is this converted into the price P of a house? P = y/(1+r) + y/(1+r)2 + … y/(1+r)n Why?

Rent and Value P = y/(1+r) + y/(1+r)2 + …+ y/(1+r)n-1 + y/(1+r)n (1) multiply both sides by (1+r)P = y + y/(1+r) + … + y/(1+r)n-1 (2) Subtract (2) – (1) r. P = y - y/(1+r)n (3) As n gets infinite, we lose the second term. r. P = y/r (3′)

Rent and Value So, with y as the annual value of housing services. P = y/r. We can rewrite this as P = Dy, where D = 1/r If r is 0. 05, then D = 20, and P = 20 y. Houses don’t last infinitely, So D < 20.

If Asset is taxed at Rate t Price = Stream of Returns – Stream of Tax Liabilities P = Dy – D(t. P), where t. P = tax liabilities P(1 + Dt) = Dy P = Dy / (1 + Dt) Price falls because the asset is taxed, but If the taxes buy X, then Higher y, X increased price! P = Dy + DX – D(t. P) Higher taxes decreased price! P = D(y + X)/(1 + Dt)

PV of Housing Services Equations Pni = Dyn + D (Xi – ti. Pni) Value of House PV of Fiscal Surplus (Deficit) Bi = S Pni/n Tax Base per house (type n in municipality i) Xi = ti B i $ worth of public good/house in municipality i.

Example Suppose we had a community ONLY of small houses worth $150, 000 each. If the community wanted Xi = $5, 000 worth of public goods (schools, police, fire, etc. ) they would have to tax themselves. How much? Xi = ti B i 5, 000 = ti * 150, 000 ti = 5, 000/150, 000 = 0. 033 Why? Tax rate of 3. 33%

Value of the House What happens to the value of the house? It stays at $150, 000. Why? Because you are paying $5, 000 in taxes for something worth $5, 000 to you. In a sense buying the public good is no different than buying groceries.

Example Suppose we had a second community ONLY of big houses worth $300, 000 each. If the community wanted Xi = $5, 000 worth of public goods (schools, police, fire, etc. ) they would have to tax themselves. How much? Xi = ti B i 5, 000 = ti * 300, 000 ti = 5, 000/300, 000 = 0. 0167 Why? Tax rate of 1. 67%, or HALF the tax rate of the other community.

Example Suppose that someone who can only afford a small house, would like to pay lower taxes, like 1. 67% rather than 3. 33%, to get $5, 000 worth of public goods. Builds a house in the community of larger houses. It would seem that by building in the community of larger houses, he/she would get a fiscal surplus. It looks like he/she is getting $5, 000 worth of services, while only paying 0. 0167 * 150, 000, or $2, 500. This generates a fiscal surplus.

BUT, a couple of things happen Pni = Dyn + D (Xi – ti. Pni)Value of House 1. The fiscal surplus is an asset. Anyone else would love to get hold of this fiscal surplus. Price will be bid up until someone buying a small house will be no better off in the community of large houses, than they were in the community of small houses. [Paying less for services BUT more for housing] 2. The tax base in the community of large houses has fallen. Why? Because the “average house” is now slightly smaller.

A bunch of things happen Property tax rate in community of “big houses” rises (slightly). Value of other houses in “big” community falls. Land values for small houses in big community rise. Is this stable? No.
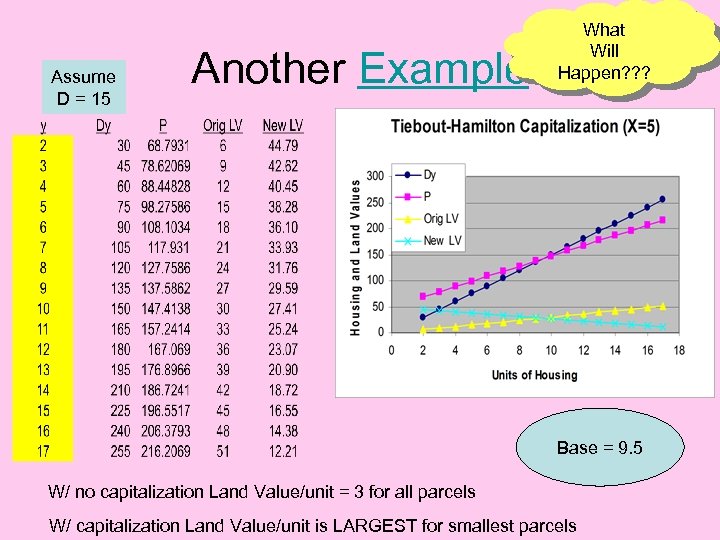
Assume D = 15 Another Example What Will Happen? ? ? Base = 9. 5 W/ no capitalization Land Value/unit = 3 for all parcels W/ capitalization Land Value/unit is LARGEST for smallest parcels

So, what then … • Does this explain “large lot zoning? ” • Is this the way that developers develop? • Are there enough different communities for this to occur. • We’ll look at some empirical stuff next time.
27b3f77042f217a8ba8c1fb0b844ec8f.ppt