Психолога нерідко інтересує питання як пов язані між собою

Психолога нерідко інтересує питання: як пов’язані між собою дві або більша кількість змінних в одній або декількох групах, що вивчаються. Наприклад: чи можуть учні з високим рівнем тривожності демонструвати стабільні академічні досягнення або з чим більше пов’язаний рівень мисленевого розвитку учнів – з їх успішністю з математики або з літератури тощо? Кореляційний аналіз досліджує наявність і характер зв’язків між випадковими величинами Х і У – ознаками генеральної сукупності. Кореляція ( від лат. correlatio - співвідношення) – залежність між подіями, явищами або величинами, що не має строго функціонального характеру. Якщо при функціональній залежності Y=f(X) кожному значенню незалежної змінної X відповідає певне значення залежної Y, то при кореляційній залежності можна говорити лише про імовірності значень залежної величини, що відповідають певному значенню величини залежної. Зв’язки між психологічними ознаками мають не функціональний, а статистичний характер - у середньому певному значенню однієї ознаки, відповідає не одне яке–небудь значення, а цілий спектр, числових значень, розподілених за варіаційним рядом, такого роду залежності між змінними величинами називається кореляційною, або кореляцією. Ступінь зв ’ язку між випадковими величинами Х і У визначає коефіцієнт кореляції

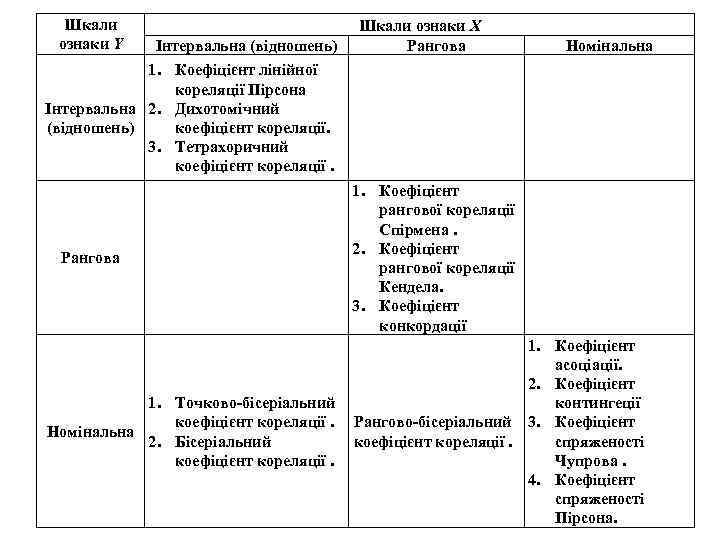
Шкали ознаки Y Інтервальна (відношень) Шкали ознаки X Рангова Номінальна 1. Коефіцієнт лінійної кореляції Пірсона Інтервальна 2. Дихотомічний коефіцієнт кореляції. (відношень) 3. Тетрахоричний коефіцієнт кореляції. Рангова 1. Точково-бісеріальний коефіцієнт кореляції. Номінальна 2. Бісеріальний коефіцієнт кореляції. 1. Коефіцієнт рангової кореляції Спірмена. 2. Коефіцієнт рангової кореляції Кендела. 3. Коефіцієнт конкордації 1. Коефіцієнт асоціації. 2. Коефіцієнт контингеції Рангово-бісеріальний 3. Коефіцієнт кореляції. спряженості Чупрова. 4. Коефіцієнт спряженості Пірсона.

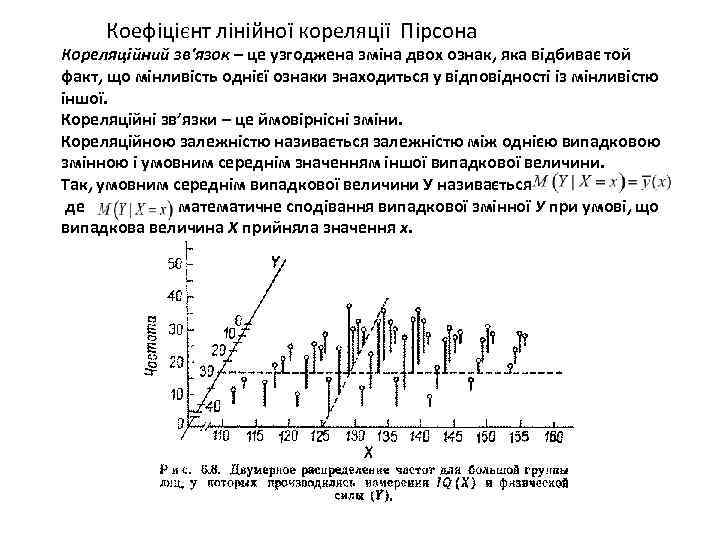
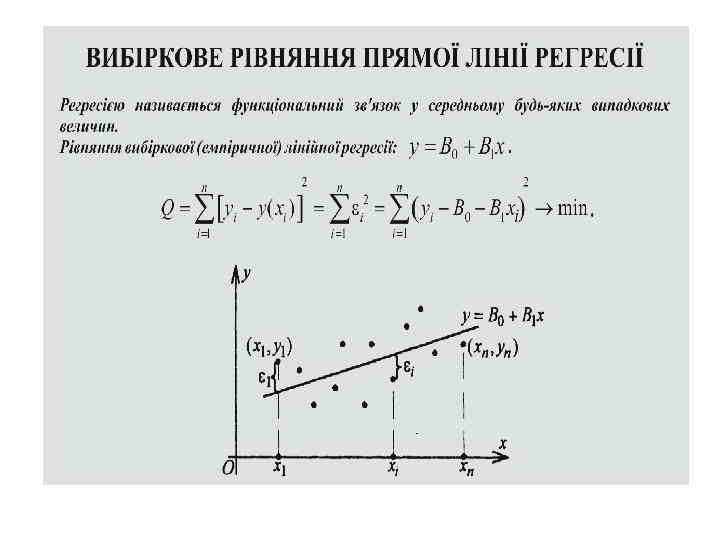
Коефіцієнт лінійної кореляції Пірсона Кореляційний зв'язок – це узгоджена зміна двох ознак, яка відбиває той факт, що мінливість однієї ознаки знаходиться у відповідності із мінливістю іншої. Кореляційні зв’язки – це ймовірнісні зміни. Кореляційною залежністю називається залежністю між однією випадковою змінною і умовним середнім значенням іншої випадкової величини. Так, умовним середнім випадкової величини У називається де математичне сподівання випадкової змінної У при умові, що випадкова величина Х прийняла значення х.

Парна кореляція вивчає характеристики взаємозв'язку двох випадкових величин. Підставою одержання цих характеристик служить спільний розподіл випадкових величин F(x, y)=P(X<x, Y<y). Основними кореляційними характеристиками є коефіцієнт кореляції: Вибірковий коефіцієнт кореляції

Нехай виконано n дослідів, в результаті яких одержано наступні значення величин X Y x 1 y 1 x 2 y 2 … … xi yi … … xn yn

Кореляційна залежність характеризується формою, спрямованістю і щільністю зв’язку. За формою кореляційний зв'язок може бути: прямолінійним, криволінійним. За спрямованістю кореляційний зв'язок може бути: додатним, від'ємним. Щільність кореляційного зв’язку визначається за величиною коефіцієнта кореляції. Властивості коефіцієнта кореляції 2) якщо Х та У – незалежні випадкові величини, то r=0 (обернене не є вірним) 3) якщо r= 1, то між ВВ Х та У має місце лінійна залежність

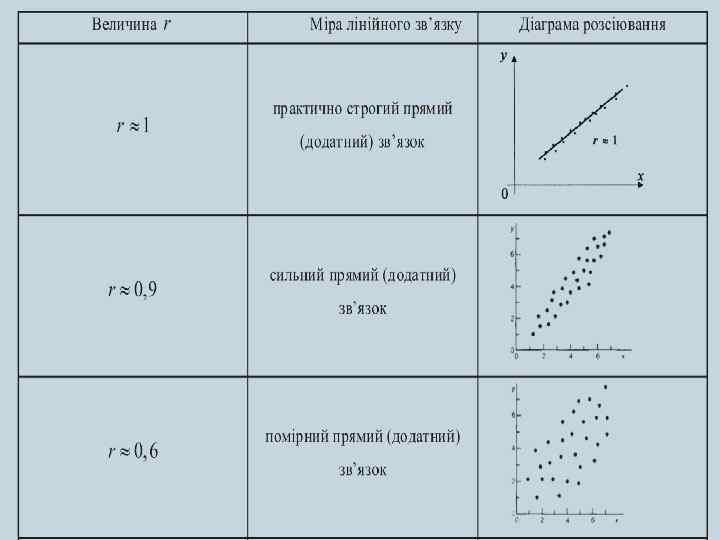
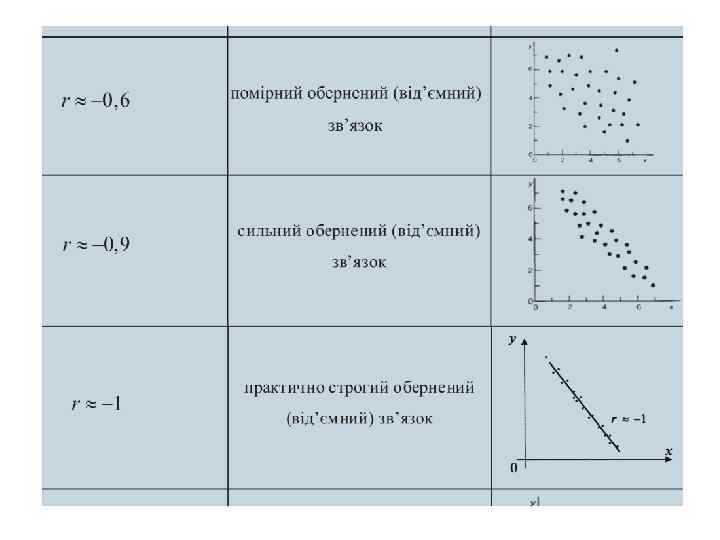
ІНТЕРПРЕТАЦІЯ ЗНАЧЕНЬ КОЕФІЦІЄНТА ЛІНІЙНОЇ КОРЕЛЯЦІЇ

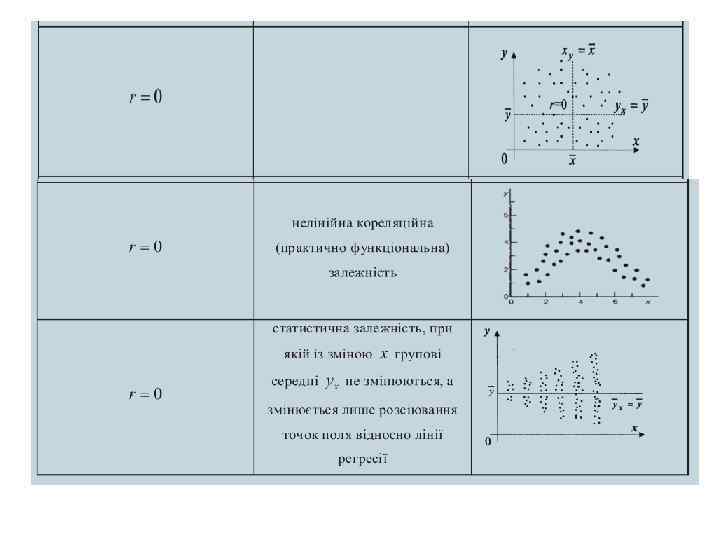
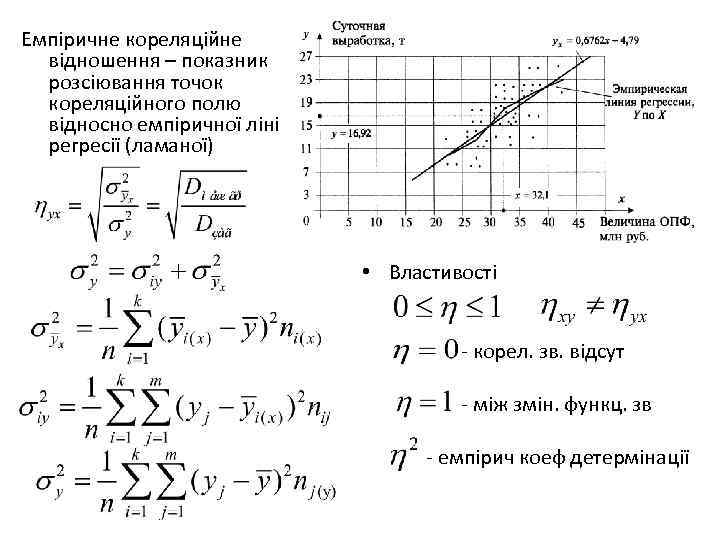
Емпіричне кореляційне відношення – показник розсіювання точок кореляційного полю відносно емпіричної лінії регресії (ламаної) • Властивості - корел. зв. відсут - між змін. функц. зв - емпірич коеф детермінації

Кореляційна матриця вибіркових коефіцієнтів кореляції Вибірковий множинний коефіцієнт кореляції - визначник кореляційної матриці - алгебраїчне доповнення елемента rii кореляційної матриці - вибірковий множинний коефіцієнт детермінації

Оцінка сили зв’язку величини Z з величинами X та Y – вибірковий сукупний коефіцієнт кореляції Оцінка сили зв’язку між Z та X вибірковий частинний коефіцієнт кореляції Оцінка сили зв’язку між Z та Y вибірковий частинний коефіцієнт кореляції між змінними Хі та Хj - алгебраїчне доповнення елемента rii кореляційної матриці - алгебраїчне доповнення елемента rjj кореляційної матриці