PSC 200 3 Descriptive Statistics Level of

PSC 200 3. Descriptive Statistics

Level of Measurement 1. Nominal 2. Ordinal 3. Interval

Lecture Overview Descriptive Statistics • Frequency Distribution • Data= Information –but too much information. How do we summarize data? • Central Measure of Tendency – Mode – Median – Mean Nominal, Ordinal, Interval • Measures of Dispersion – Variance Interval

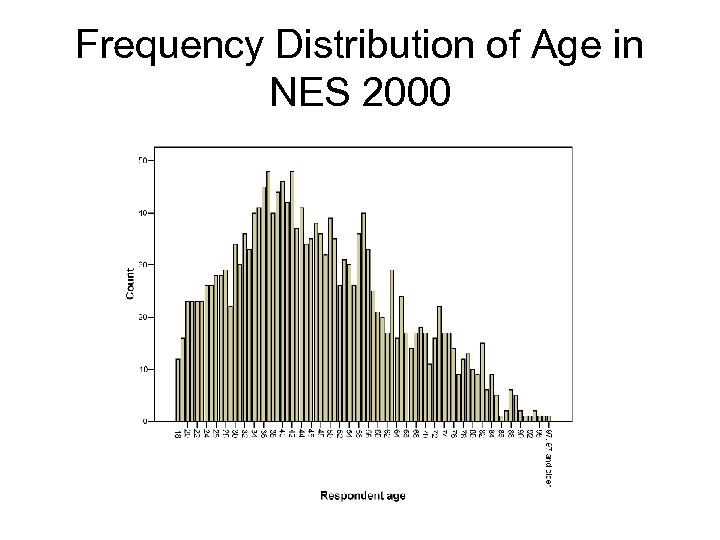Frequency Distribution of Age in NES 2000

Understanding Distributions • What is “typical”? ? Mode? Median? Mean? – – Example: 2, 2, 2, 4, 6, 8, 8 Mode: 2 Median: 4 Mean: 4. 57 • Where does each measure of central tendency apply?

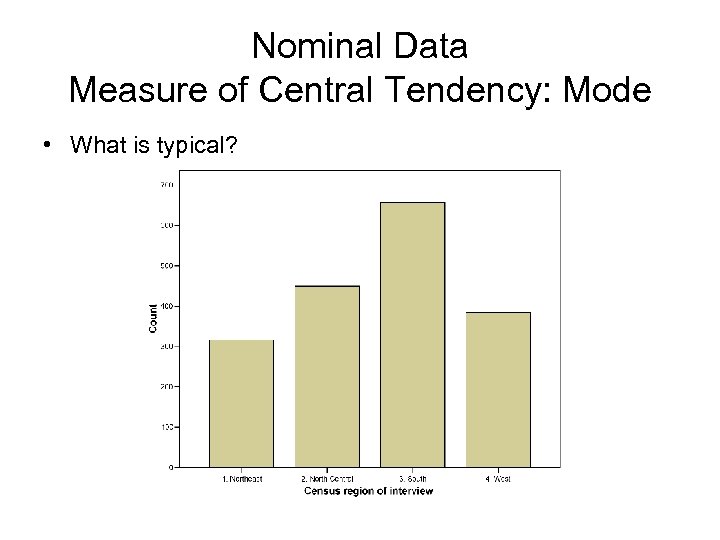Nominal Data Measure of Central Tendency: Mode • What is typical?

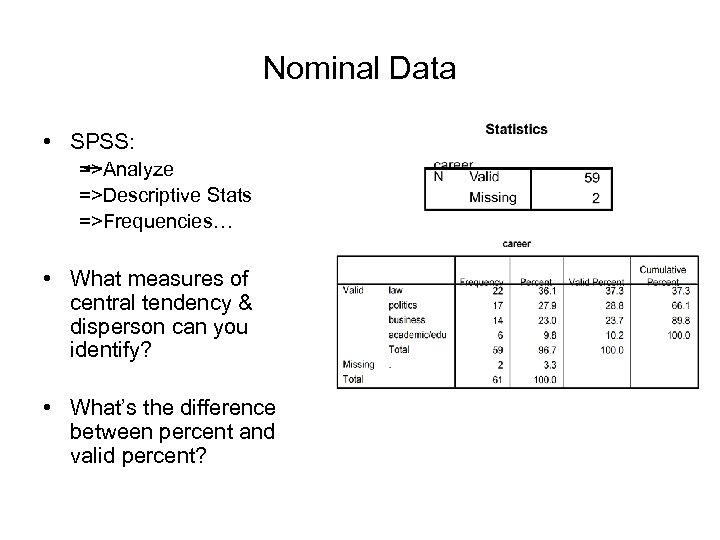Nominal Data • SPSS: =>Analyze =>Descriptive Stats =>Frequencies… • What measures of central tendency & disperson can you identify? • What’s the difference between percent and valid percent?

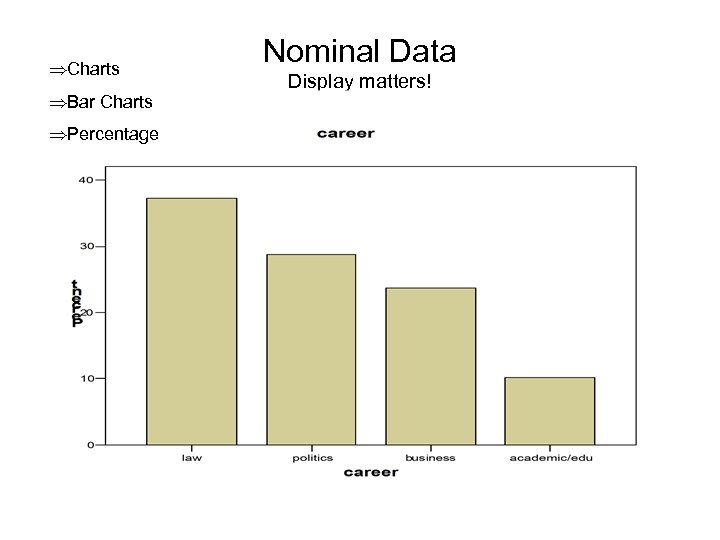ÞCharts ÞBar Charts ÞPercentage Nominal Data Display matters!

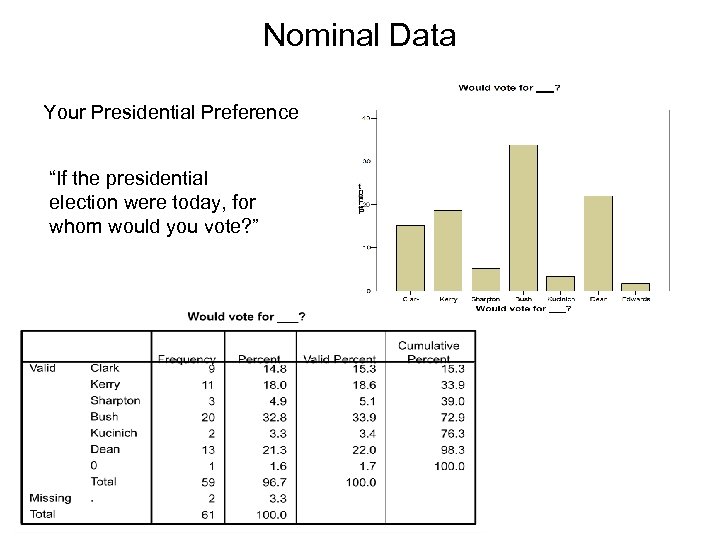Nominal Data Your Presidential Preference “If the presidential election were today, for whom would you vote? ”

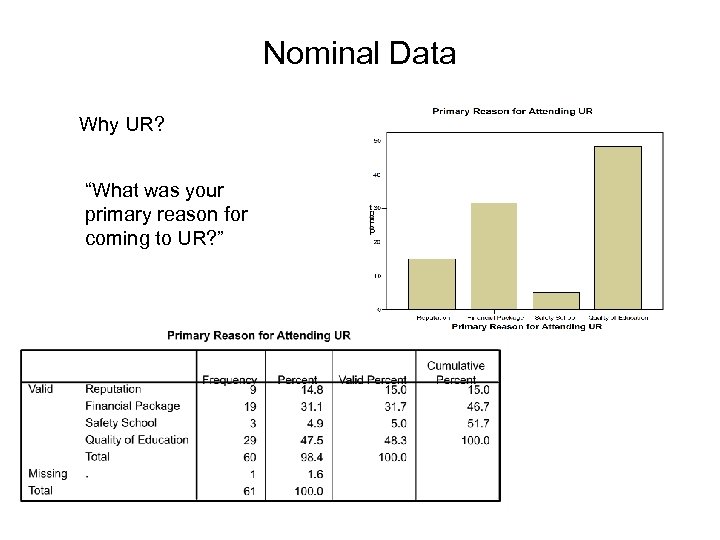Nominal Data Why UR? “What was your primary reason for coming to UR? ”

Ordinal Data • • • Sequence matters, e. g. rankings Median now has meaning Example: A 12. Approve/disapprove Clinton job Do you approve or disapprove of the way Bill Clinton is handling his job as president? 1. APPROVE 5. DISAPPROVE 8. DON'T KNOW 9. RF 0. NA --> SKIP TO B 1 Count 1 1177 5 565 8 55 9 10

A 12 a. Strength of approval/disapproval of Clinton IF R APPROVES CLINTON HANDLING JOB AS PRESIDENT/ IF R DISAPPROVES CLINTON HANDLING JOB AS PRESIDENT: Strongly or not strongly? 1. STRONGLY 5. NOT STRONGLY 8. DK 9. RF 0. NA; INAP, 8, 9, 0 in A 12 Count 0 65 1 1145 5 587 8 8 9 2

Summary: Approval/Disapproval of Clinton Job as President Do you approve or disapprove of the way Bill Clinton is handling his job as president? Strongly or not strongly? SUMMARY: APPROVAL/ DISAPPROVAL OF CLINTON JOB AS Built from A 12 and A 12 a. 1. Approve strongly 2. Approve not strongly 4. Disapprove not strongly 5. Disapprove strongly 8. DK (in A 12 or A 12 a) 9. RF (in A 12 or A 12 b) 0. NA

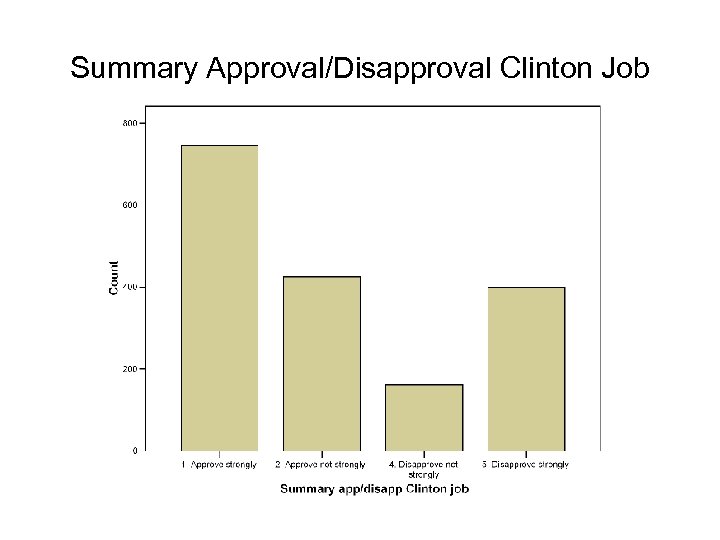Summary Approval/Disapproval Clinton Job

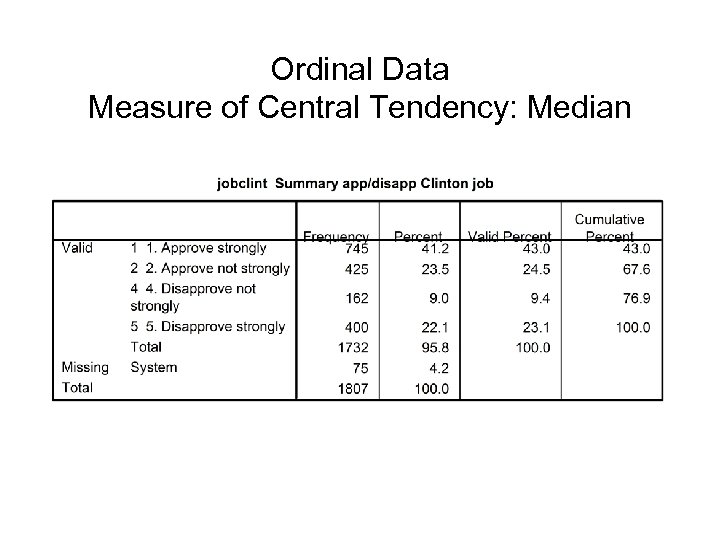Ordinal Data Measure of Central Tendency: Median

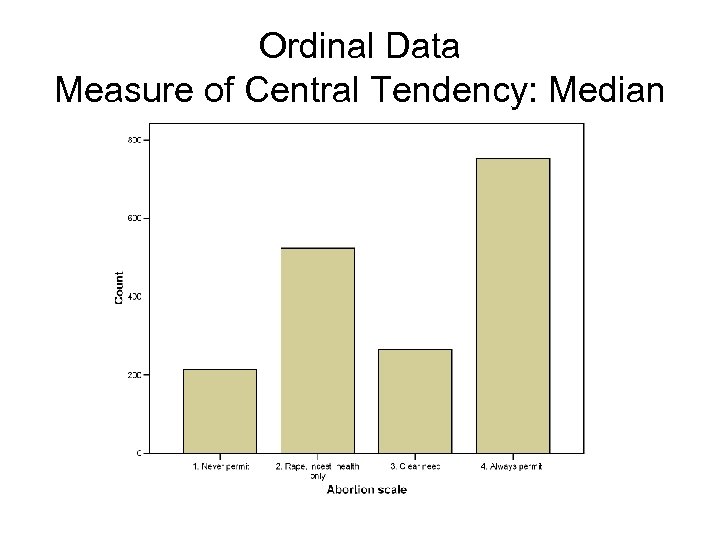Ordinal Data Measure of Central Tendency: Median

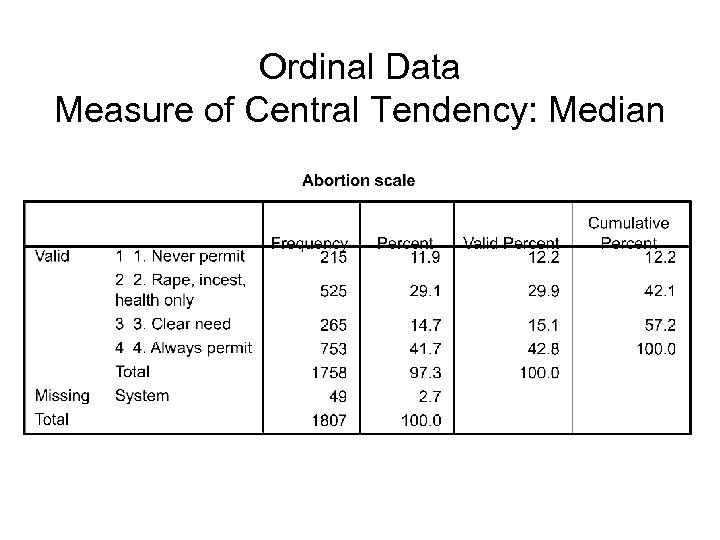Ordinal Data Measure of Central Tendency: Median

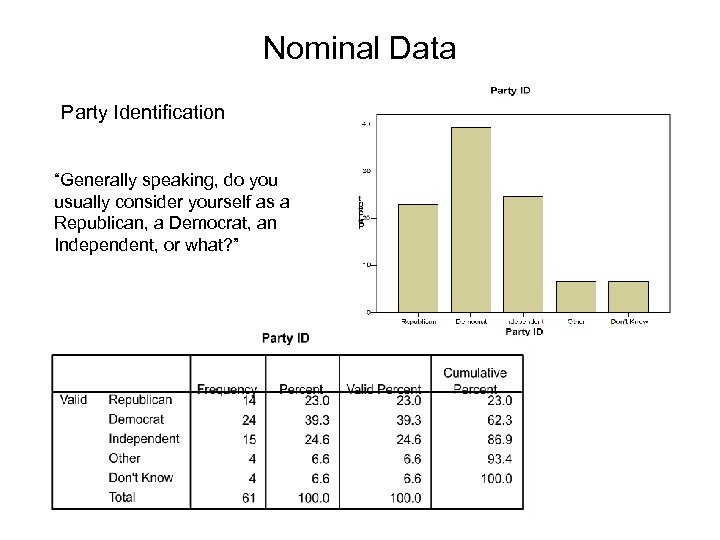Nominal Data Party Identification “Generally speaking, do you usually consider yourself as a Republican, a Democrat, an Independent, or what? ”

Interval Data • Continuous: numbers on the real line • Mean (arithmetic): • Example: 2, 3, 3, 5, 5, 6, 7, 7, 10, 201, 987 – Mean =(2+3+3+5+5+6+7+7+10+201+987)/11 = 112. 36 – Median? – Modes?

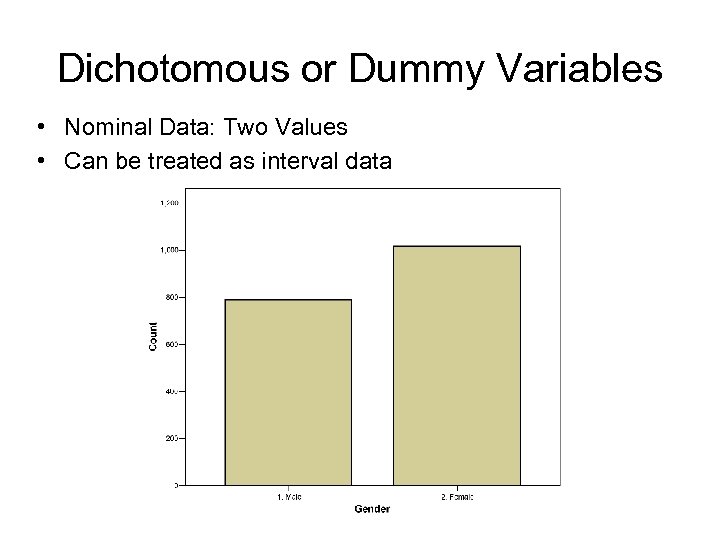Dichotomous or Dummy Variables • Nominal Data: Two Values • Can be treated as interval data

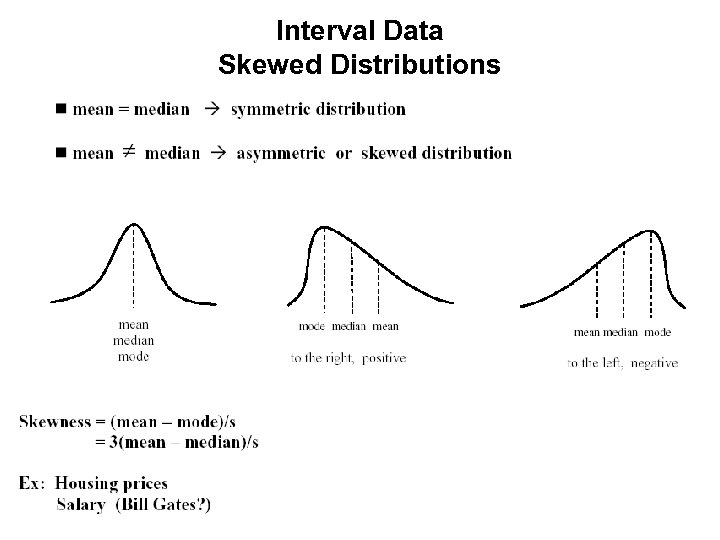Interval Data Skewed Distributions

Skewed Distributions • Skewness: – For data Y 1, Y 2, …YN Skewness = Where is the mean, s is the standard deviation, and N is the number of data points

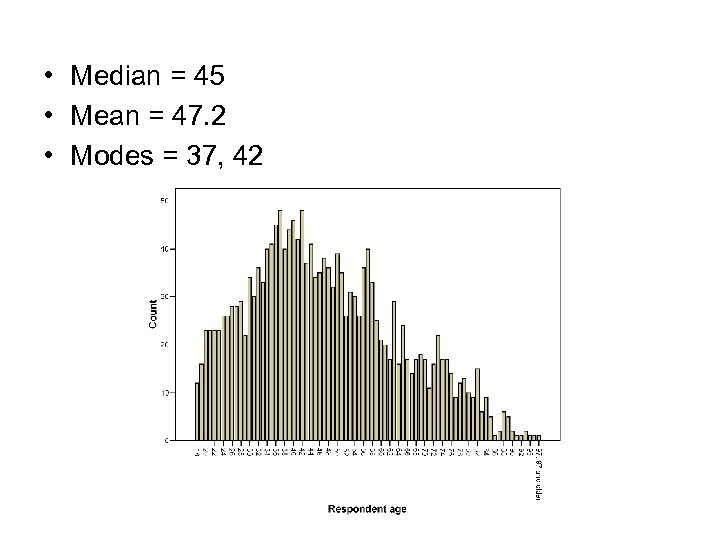• Median = 45 • Mean = 47. 2 • Modes = 37, 42

Interval Data Grouped Into Categories for Visual Presentation

Variance §How dispersed or spread out the data is §Variance is the average squared deviation from the mean §Standard Deviation = square root of variance = s

Use and Abuse of Descriptive Stats

Grofman, Koetzle, Mc. Gann. LSQ 2002. Congressional Leadership, 1965 -96 • Are congressional leaders more extreme than their followers? • Discern between theories that claim that – leaders are more extreme – leaders are more centrist

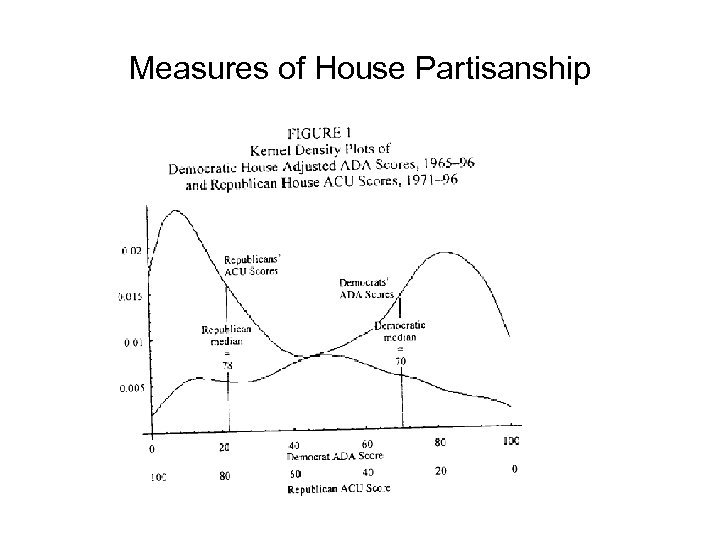Measures of House Partisanship

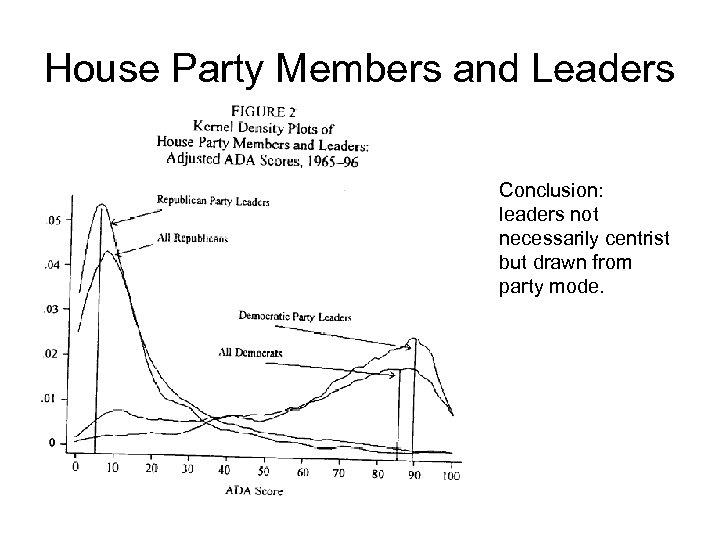House Party Members and Leaders Conclusion: leaders not necessarily centrist but drawn from party mode.

Gary Jacobson. 1987. The Marginals Never Vanished. AJPS. • “Marginal” – competitive elections • Do incumbents have a growing advantage in elections? • Do they win elections more easily than in the past? • Has electoral competition declined? Incumbent behavior changed? • Implications for democracy…

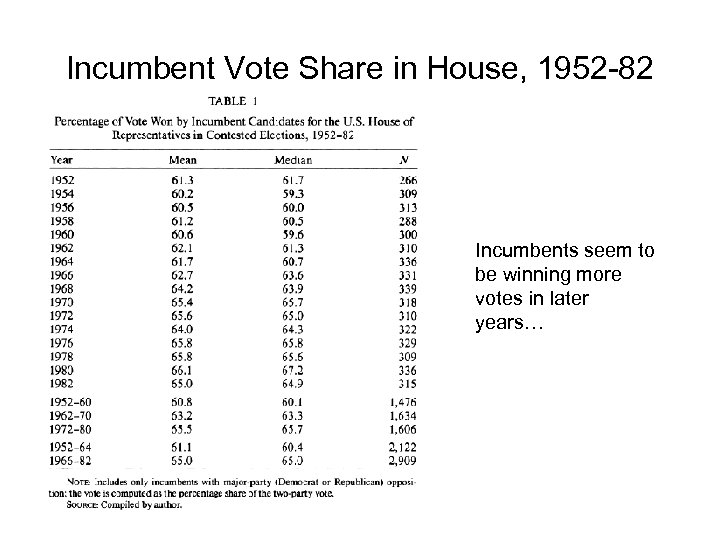Incumbent Vote Share in House, 1952 -82 Incumbents seem to be winning more votes in later years…

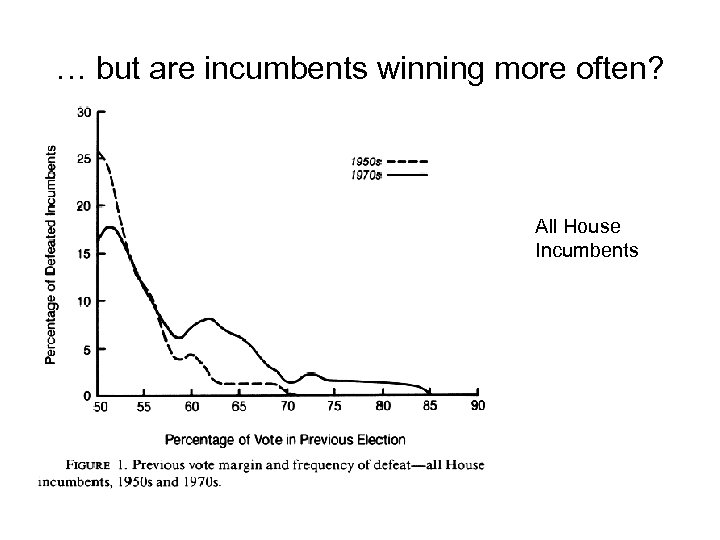… but are incumbents winning more often? All House Incumbents

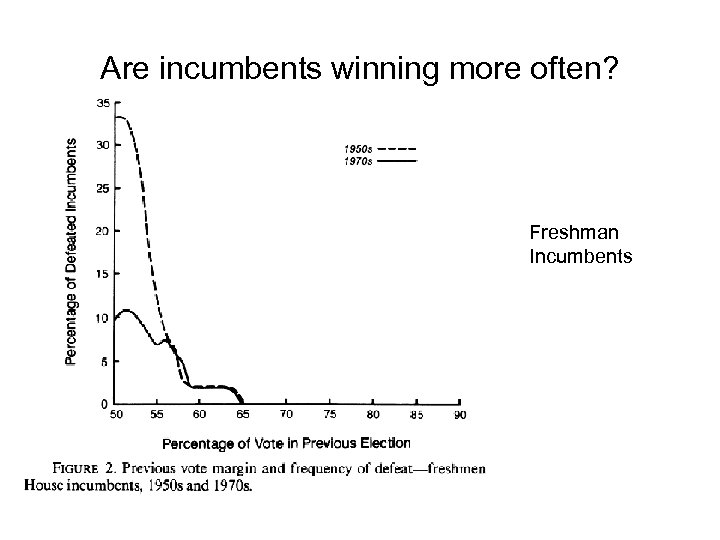Are incumbents winning more often? Freshman Incumbents

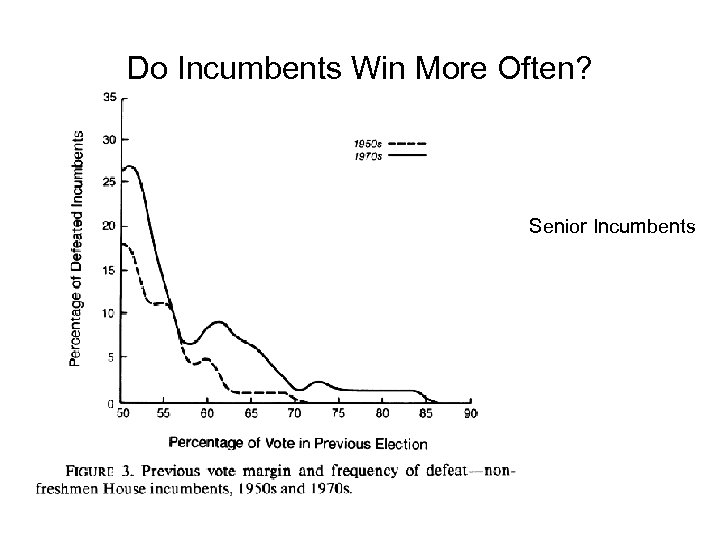Do Incumbents Win More Often? Senior Incumbents

Jacobson’s Conclusion • No net change in overall security for incumbents (same proportion, ca. 6 -7%, lose) • Marginals do increase but so does vote swing. • First-term incumbents safer, senior incumbents not • Explains absence of change in incumbent behavior