Прямой (плоский)_изгиб.ppt
- Количество слайдов: 25
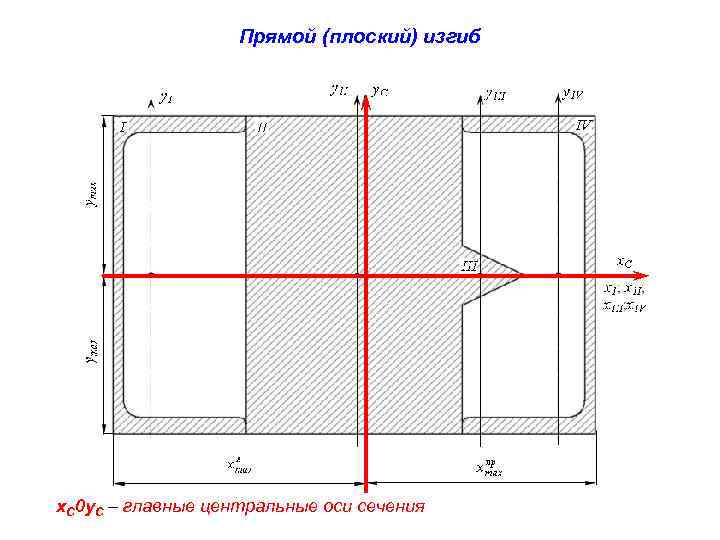
Прямой (плоский) изгиб x. C 0 y. C – главные центральные оси сечения
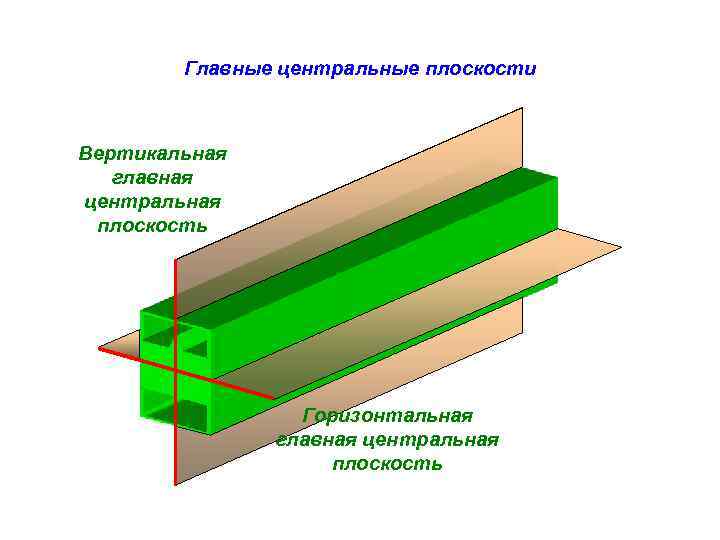
Главные центральные плоскости Вертикальная главная центральная плоскость Горизонтальная главная центральная плоскость
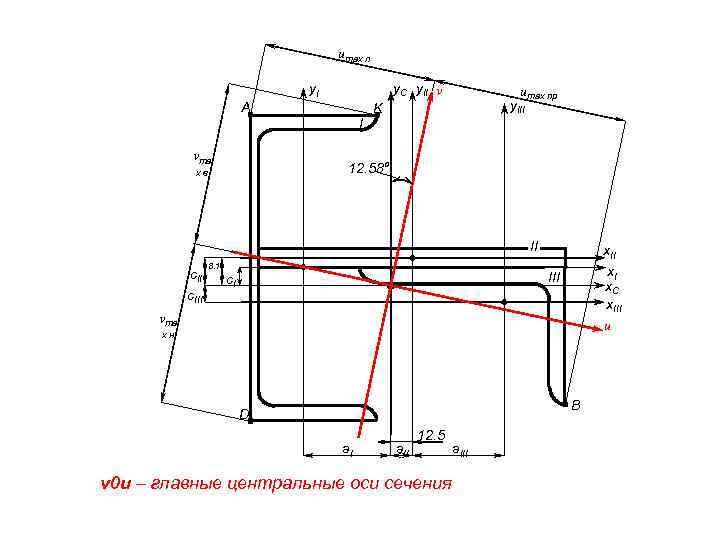
umax л y. C y. II v y. I A I vma umax пр y. III K 12. 58º xв II c. III 8. 1 x. II x. C x. III c. I vma u xн B D a. II 12. 5 v 0 u – главные центральные оси сечения a. III
v u
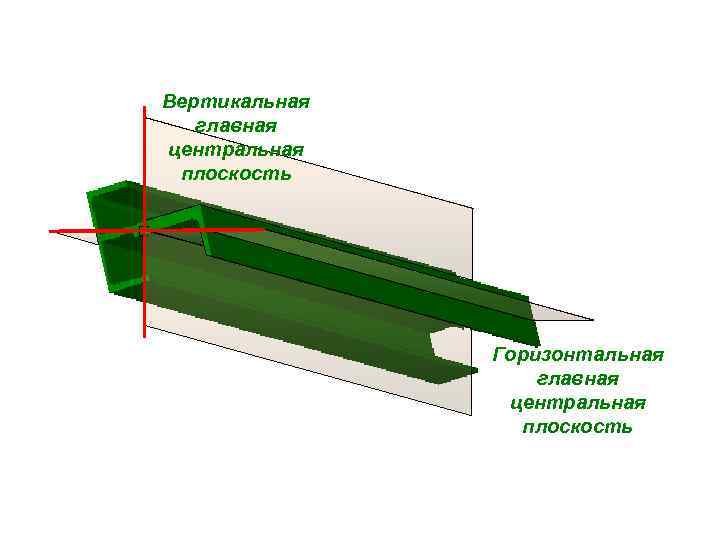
Вертикальная главная центральная плоскость Горизонтальная главная центральная плоскость
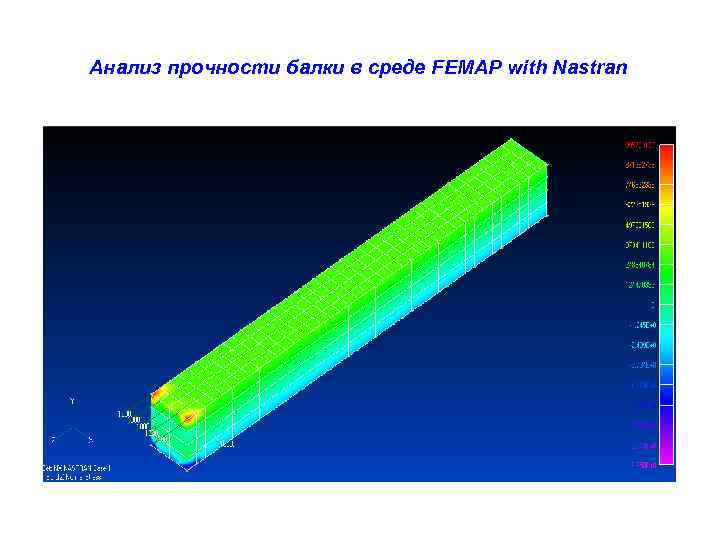
Анализ прочности балки в среде FEMAP with Nastran

Анализ прочности балки в среде FEMAP with Nastran

Деформированное состояние балки
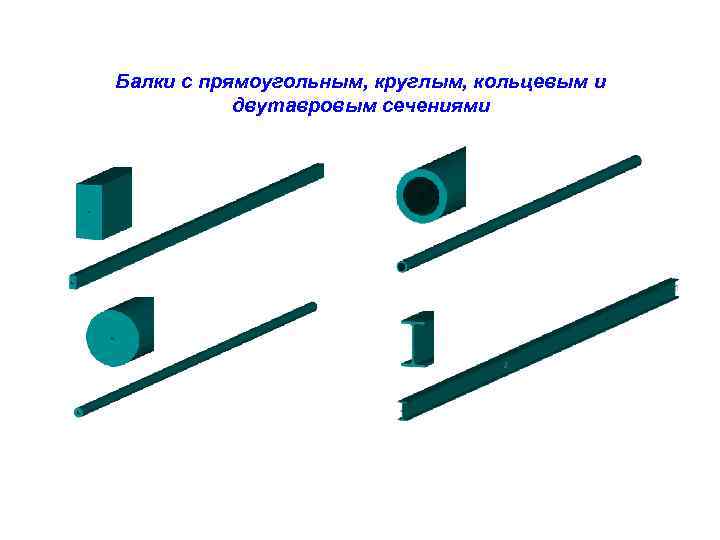
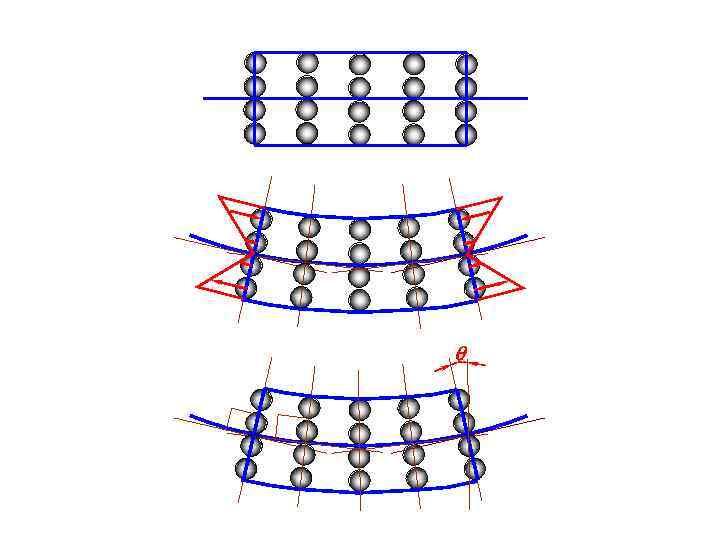
Балки с прямоугольным, круглым, кольцевым и двутавровым сечениями
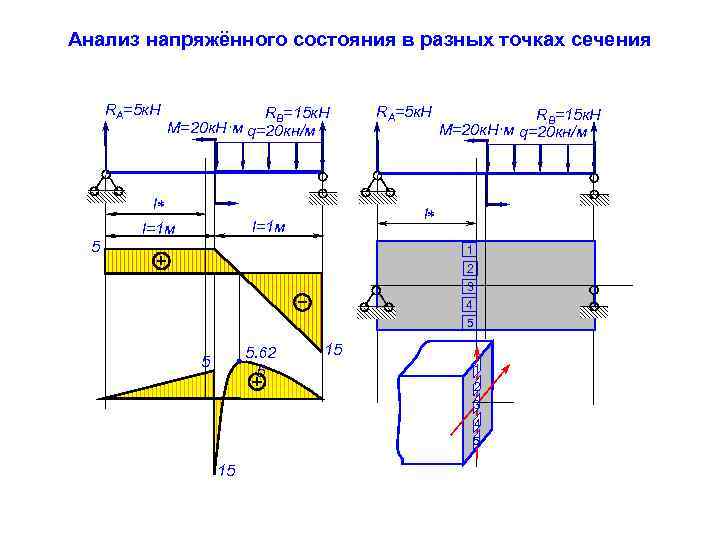
Анализ напряжённого состояния в разных точках сечения RA=5 к. Н RB=15 к. Н M=20 к. Н·м q=20 кн/м l 5 RB=15 к. Н M=20 к. Н·м q=20 кн/м l l=1 м RA=5 к. Н 1 2 3 4 5 5. 62 5 5 15 1 2 3 4 5 15
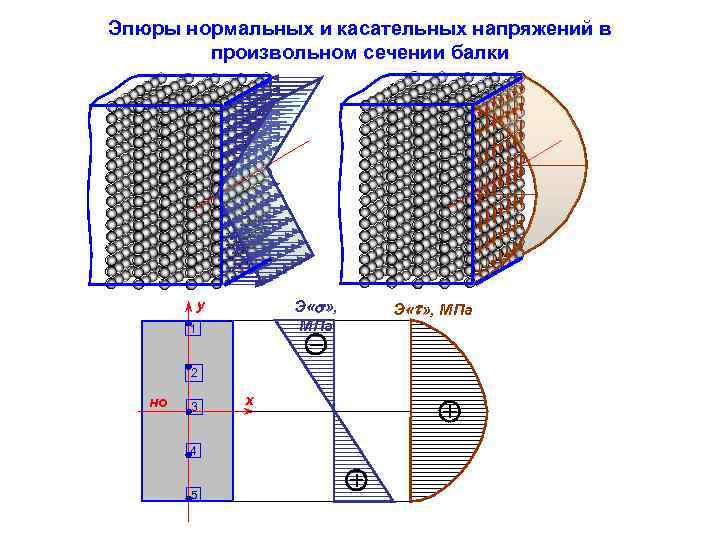
Эпюры нормальных и касательных напряжений в произвольном сечении балки Э « » , МПа y 1 2 но 3 4 5 x Э « » , МПа
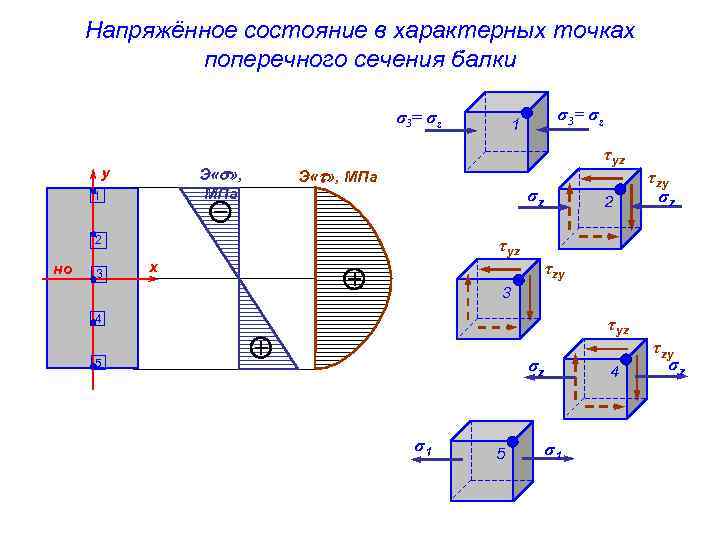
Напряжённое состояние в характерных точках поперечного сечения балки σ3 = σz Э « » , МПа y 1 τyz Э « » , МПа σz 2 но 3 σ3 = σz 1 2 τzy σz τyz τzy x 3 4 τyz σz 5 σ1 5 4 σ1 τzy σz
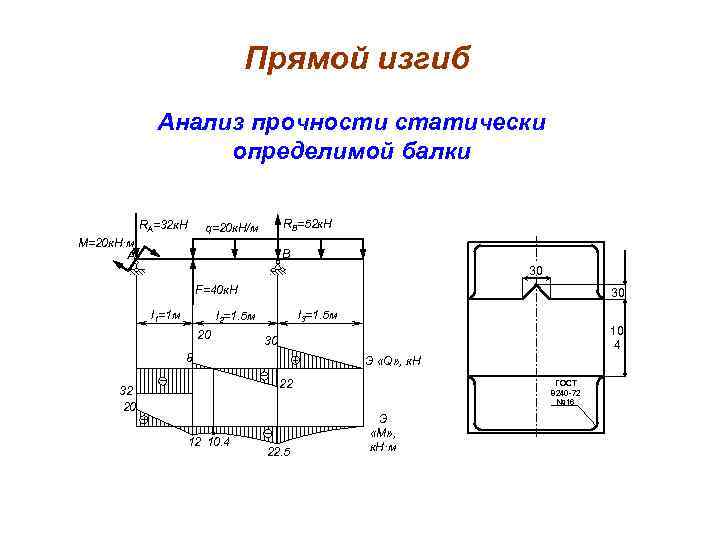
Прямой изгиб Анализ прочности статически определимой балки RA=32 к. Н RB=52 к. Н q=20 к. Н/м M=20 к. Н·м A B 30 F=40 к. Н l 1=1 м 30 l 3=1. 5 м l 2=1. 5 м 20 10 4 30 8 Э «Q» , к. Н 22 32 20 12 10. 4 22. 5 ГОСТ 8240 -72 № 16 Э «M» , к. Н·м
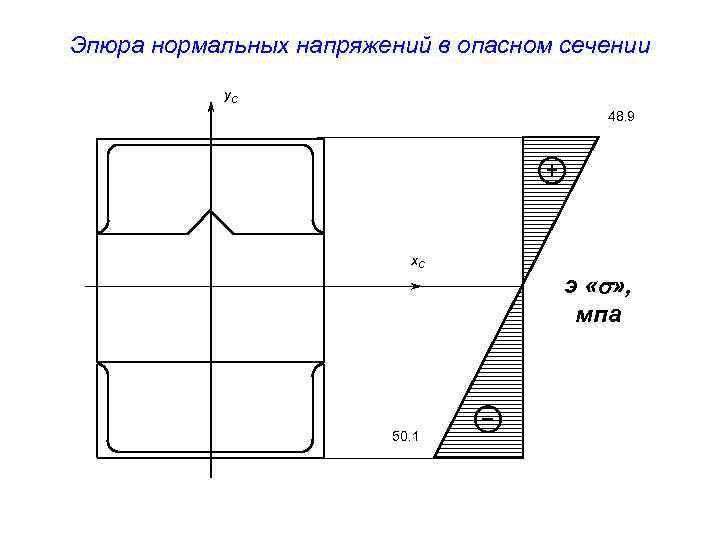
Эпюра нормальных напряжений в опасном сечении y. C 48. 9 x. C 50. 1 э « » , мпа
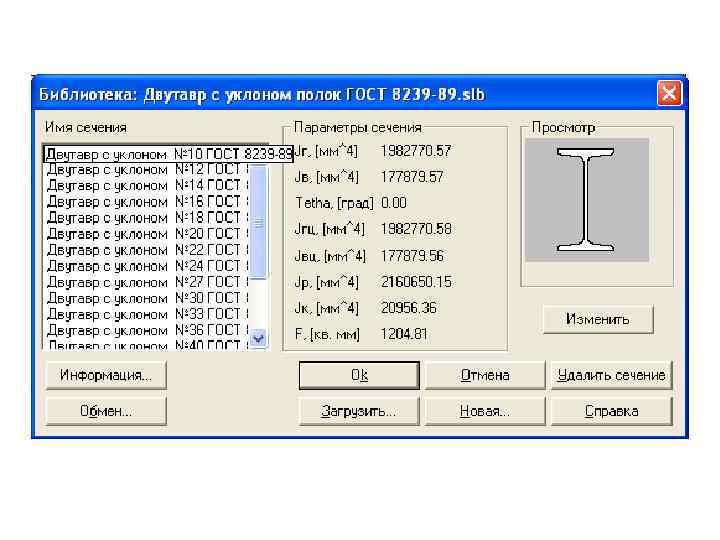
Решение проблемы с помощью модуля APM Structure 3 D
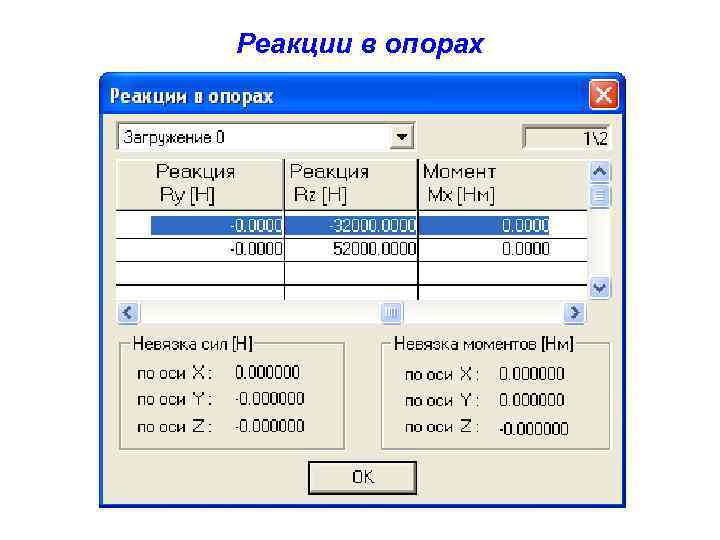
Реакции в опорах
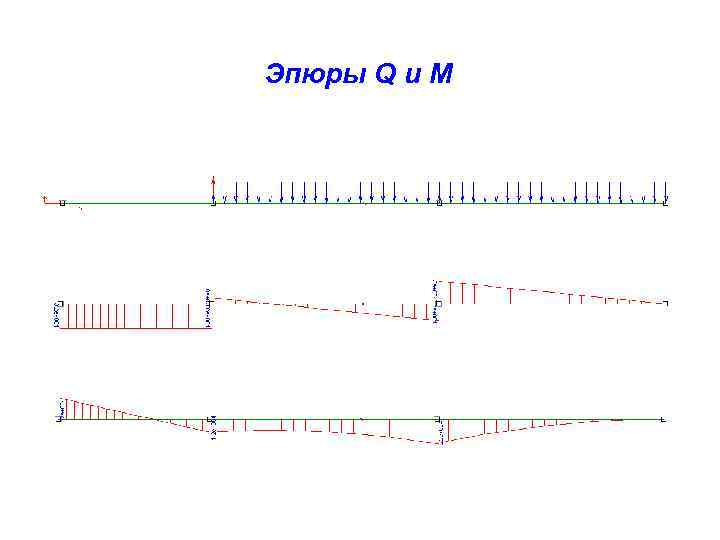
Эпюры Q и M
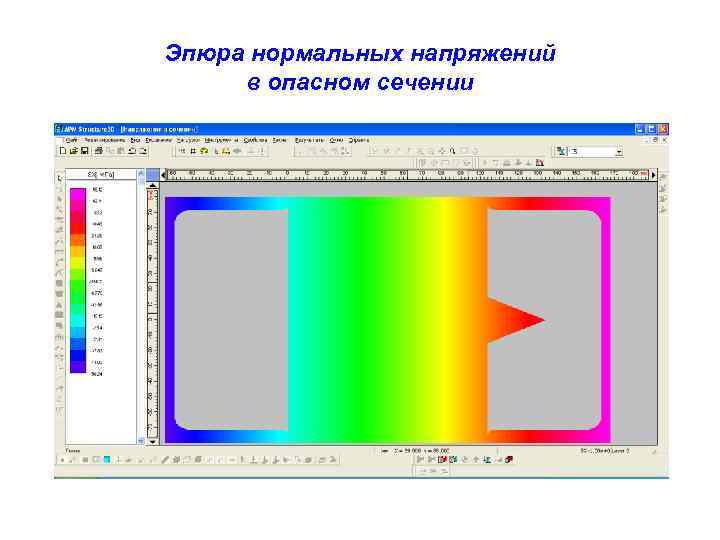
Эпюра нормальных напряжений в опасном сечении
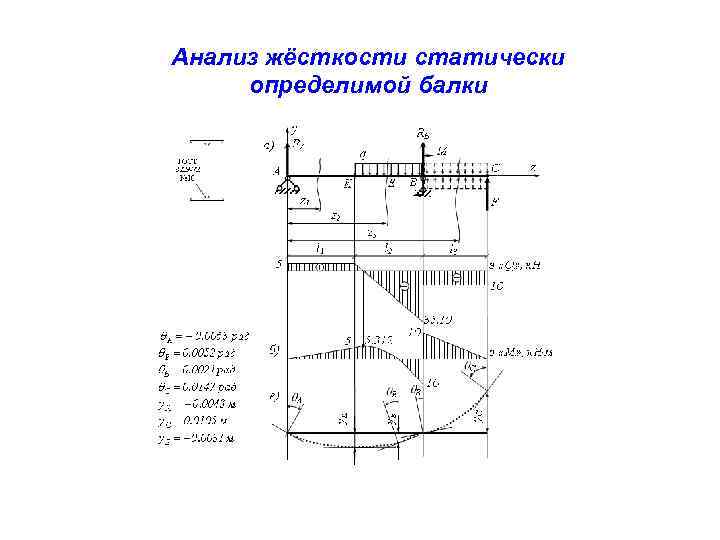
Анализ жёсткости статически определимой балки
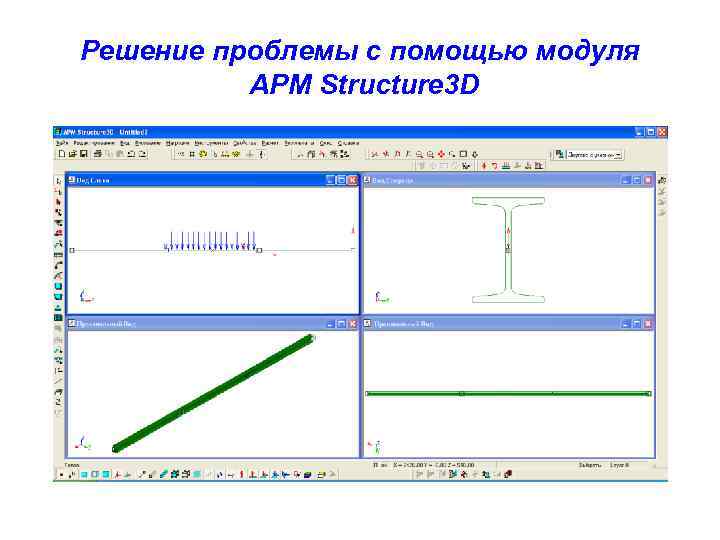
Решение проблемы с помощью модуля APM Structure 3 D
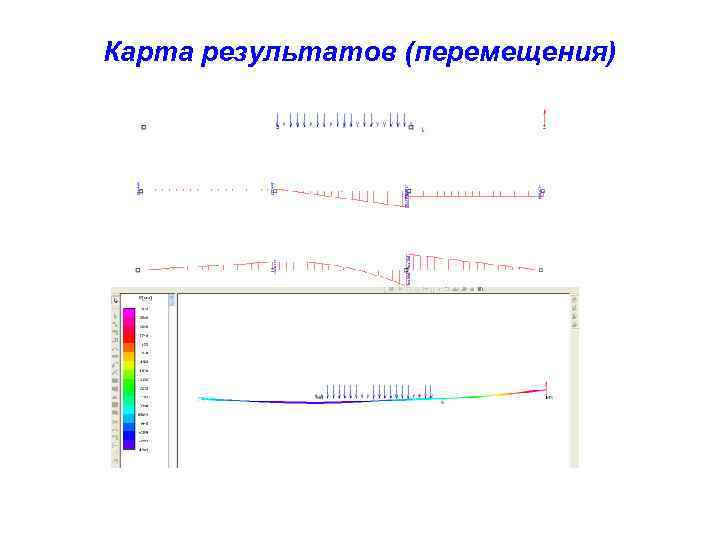
Карта результатов (перемещения)
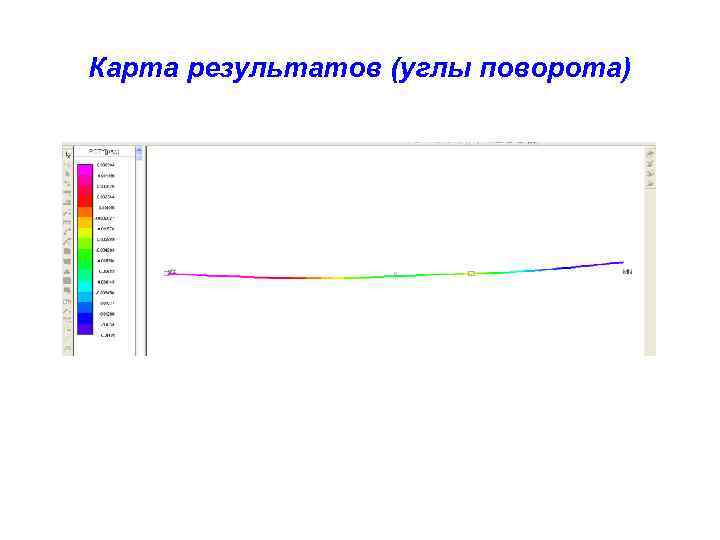
Карта результатов (углы поворота)
Прямой (плоский)_изгиб.ppt