Прямая Прямые общего положения n Прямые не

Зарегистрируйтесь, чтобы просмотреть полный документ!

РЕГИСТРАЦИЯ

Прямая

Прямые общего положения n Прямые, не параллельные и не перпендикулярные плоскостям проекций

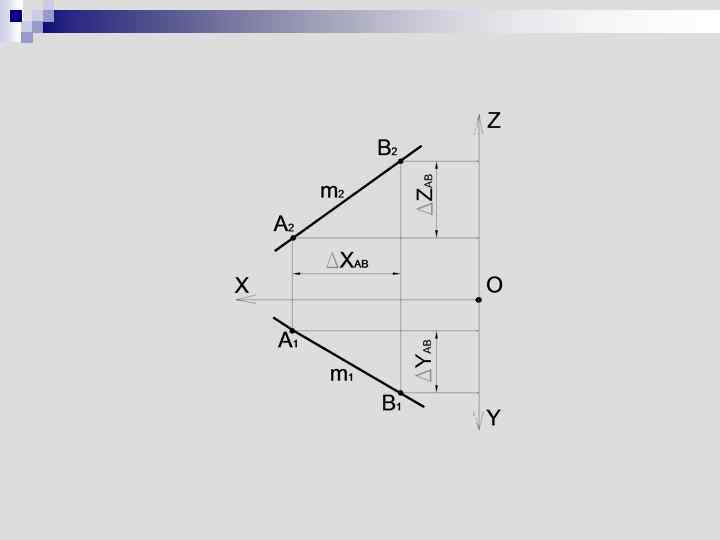
Частное положение прямой в пространстве

Прямые, параллельные плоскостям проекций – линии уровня Горизонтальная прямая (горизонталь) параллельна П 1 n Фронтальная прямая (фронталь) параллельна П 2 n Профильная прямая параллельна П 3 n

Z = const A 1 B 1=IABI A 1 B 1^OX=AB^П 2=Ѱ

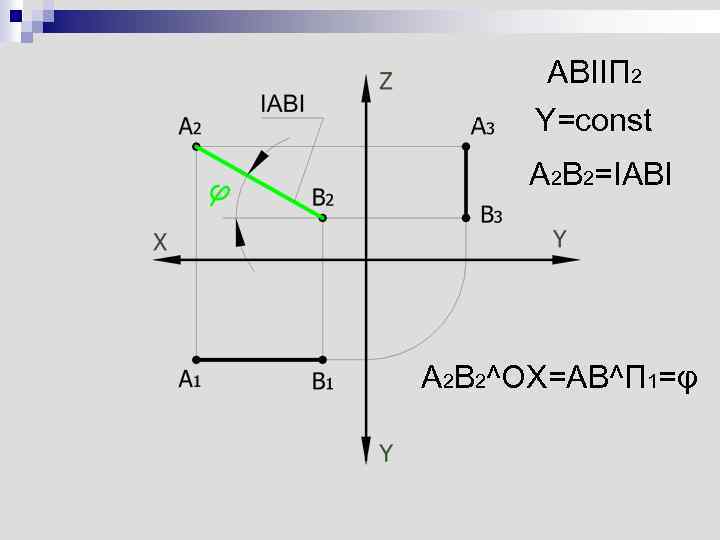
ABIIП 2 Y=const A 2 B 2=IABI A 2 B 2^OX=AB^П 1=φ

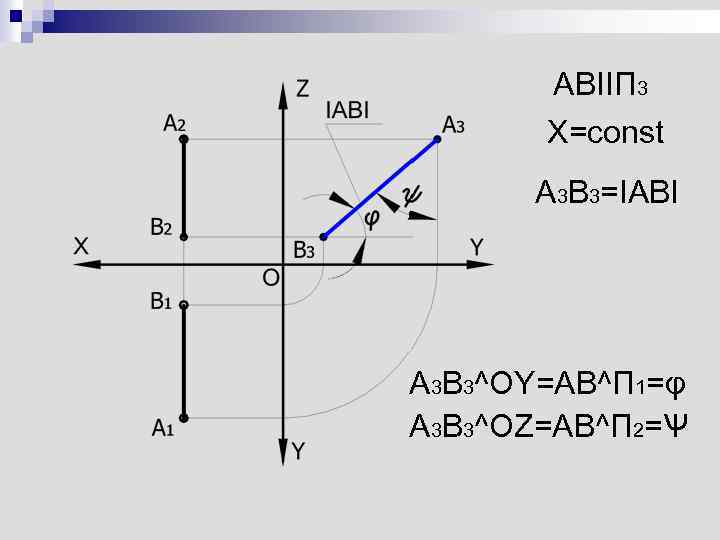
ABIIП 3 X=const A 3 B 3=IABI A 3 B 3^OY=AB^П 1=φ A 3 B 3^OZ=AB^П 2=Ѱ

Прямые, перпендикулярные плоскостям проекций Горизонтально проецирующая прямая П 1 n Фронтально проецирующая прямая П 2 n Профильно проецирующая прямая П 3 n

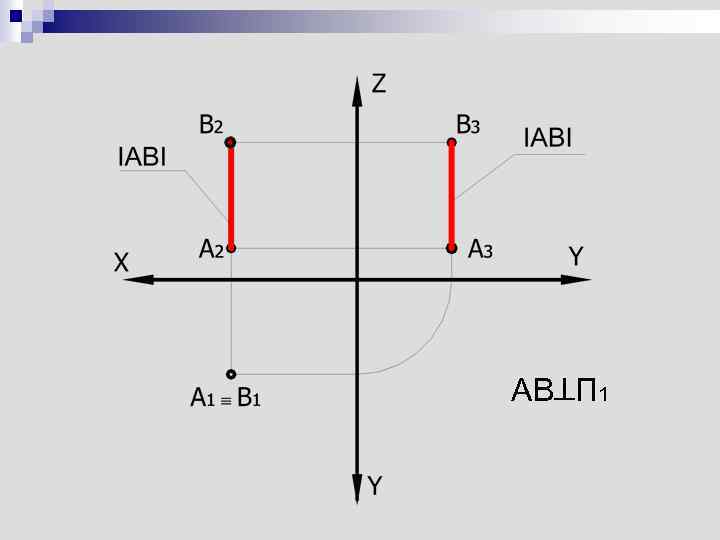
AB П 1

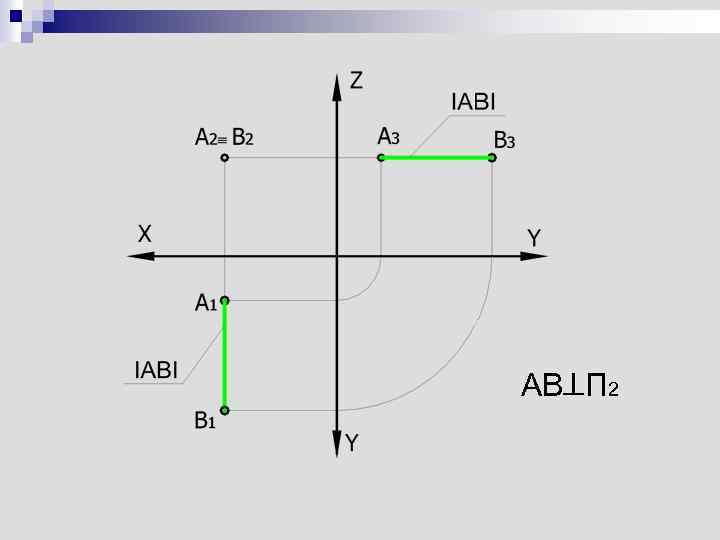
AB П 2

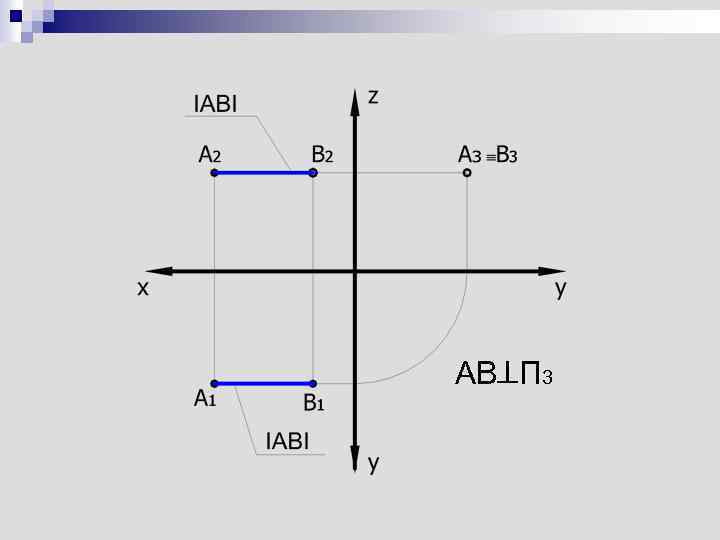
AB П 3

Относительное положение прямой и точки n Проекции точки, принадлежащей прямой, должны принадлежать соответствующим проекциям этой прямой К a ⇨ K 1 a 1 K 2 a 2 K 3 a 3

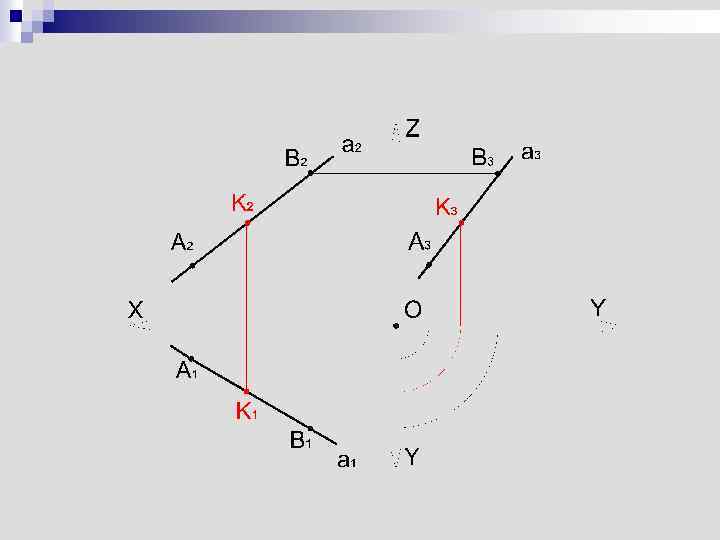
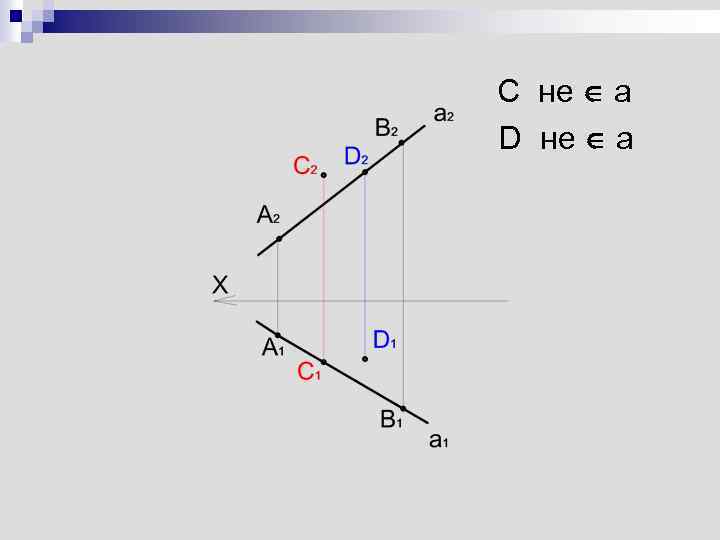
C не a D не a

Следы прямой линии n След прямой – это точка пересечения прямой с плоскостью проекций AB ∩ П 1=M – горизонтальный след AB AB ∩ П 2=N – фронтальный след AB

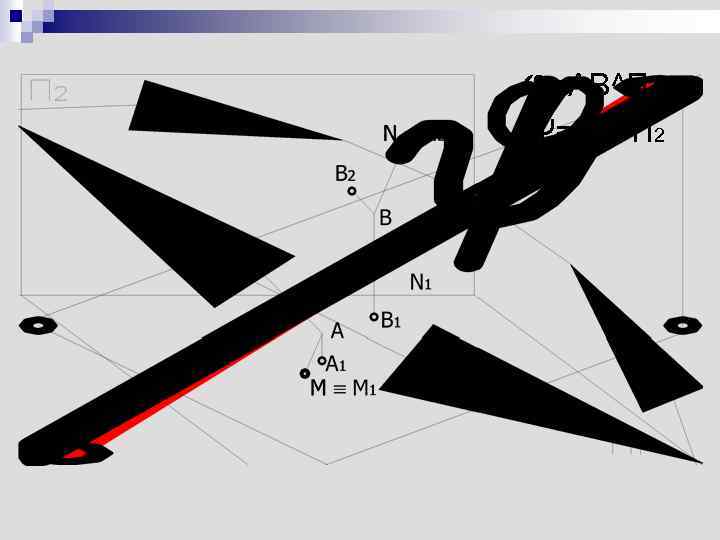
φ=AB^П 1 Ѱ=AB^П 2

M=AB∩П 1⇨ZM=0 M(M 1, M 2) N=AB∩П 2⇨YM=0 N(N 1, N 2)

Определение длины отрезка и углов наклона его к плоскостям проекций n Способ прямоугольного треугольника

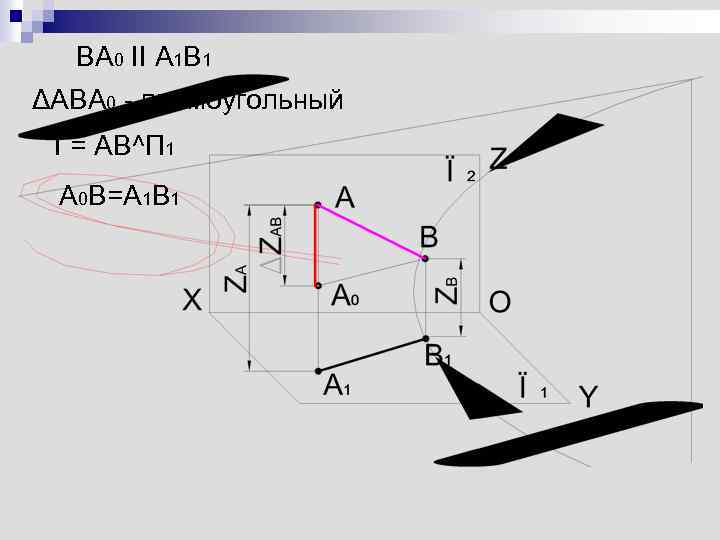
BA 0 II A 1 B 1 ΔABA 0 - прямоугольный f = AB^П 1 A 0 B=A 1 B 1

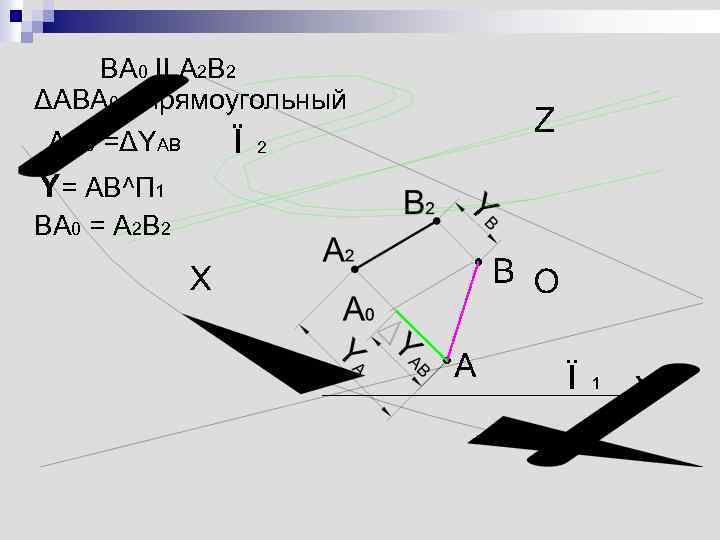
BA 0 II A 2 B 2 ΔABA 0 - прямоугольный AA 0 =ΔYAB Y= AB^П 1 BA 0 = A 2 B 2

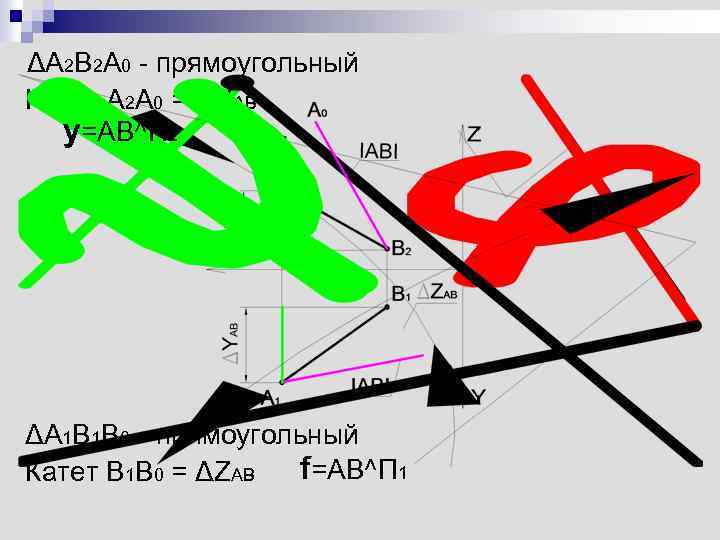
ΔA 2 B 2 A 0 - прямоугольный Катет A 2 A 0 = ΔYAB y=AB^П 2 ΔA 1 B 1 B 0 - прямоугольный f=AB^П 1 Катет В 1 B 0 = ΔZAB

Построение чертежа отрезка прямой по заданным условиям n. Задача Построить проекции отрезка АВ длиной 50 мм с углами наклона к плоскостям проекций f= AB^П 1= 30° y= AB^П 2 = 45° X A < XB YA > Y B ZA > ZB

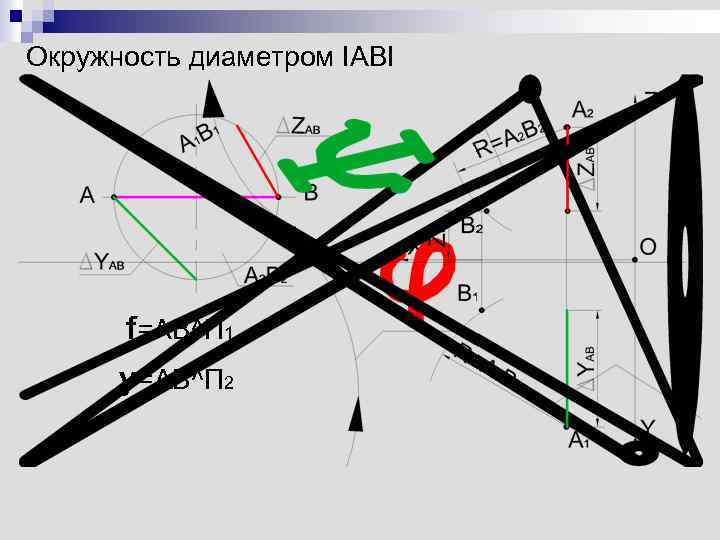
Окружность диаметром IABI f=AB^П 1 y=AB^П 2

Относительное положение прямых Пересекающиеся прямые m ∩ n = A n Параллельные прямые m II n n Скрещивающиеся прямые m ÷ n n

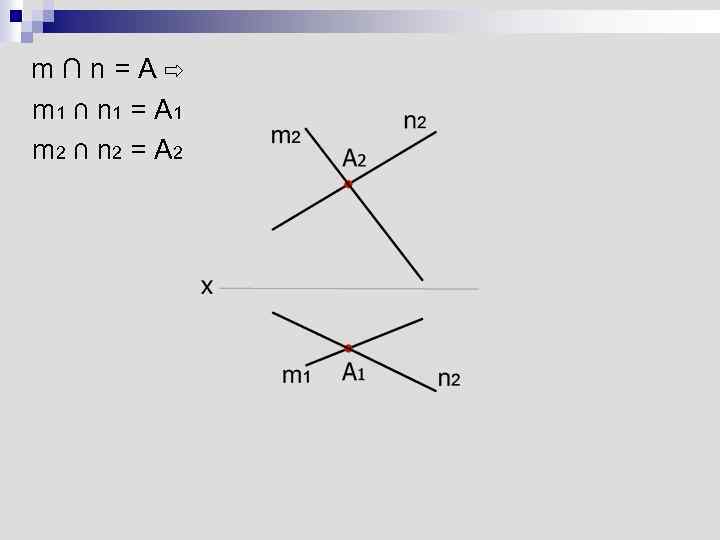
m∩n=A⇨ m 1 ∩ n 1 = A 1 m 2 ∩ n 2 = A 2

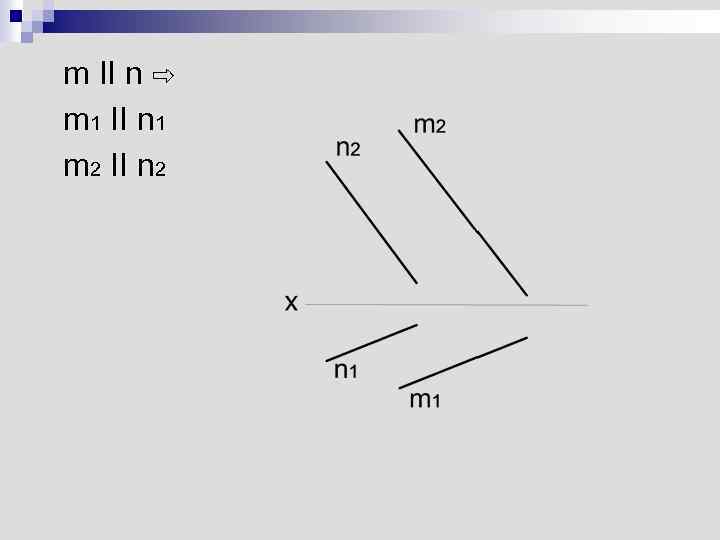
m II n ⇨ m 1 II n 1 m 2 II n 2

Скрещивающиеся прямые Метод конкурирующих точек n Конкурирующие точки – это точки, расположенные на одном проецирующем луче n Метод конкурирующих точек используется для определения видимости геометрических элементов

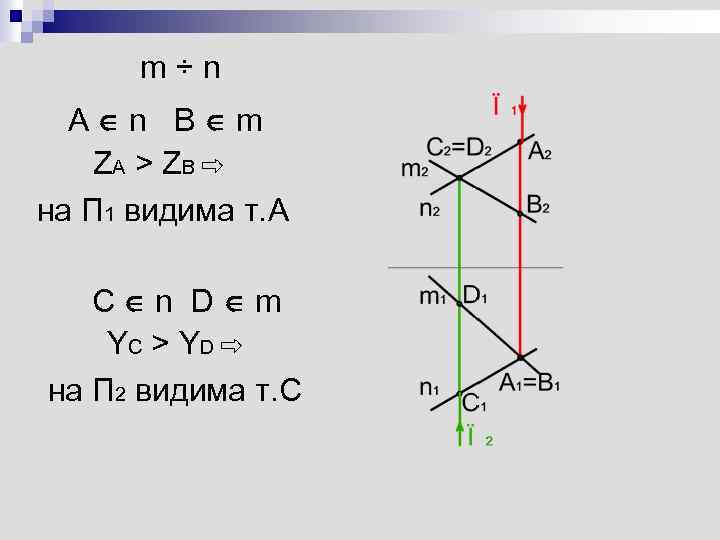
m÷n A n B m ZA > Z B ⇨ на П 1 видима т. A C n D m YC > Y D ⇨ на П 2 видима т. С

Скачать презентацию Прямая Прямые общего положения n Прямые не

Лекция 2.Прямая.ppt

Количество слайдов: 29