Прямая на плоскости 1 Основным предметом изучения

Прямая на плоскости. 1

Основным предметом изучения в аналитической геометрии являются линии, определяемые по отношению к декартовым прямоугольным координатам алгебраическими уравнениями. На плоскости это уравнения следующего вида: Ax + By + C = 0; Ax 2 + By 2 + Cxy+ Dx + Ey+ F = 0; Определение. Линия, которая в некоторой системе декартовых прямоугольных координат определяется алгебраическим уравнением степени n, называется алгебраической кривой n –ого порядка. 2

Виды уравнений прямой на плоскости. Прямая на плоскости может быть задана одним из следующих ниже уравнений. 1. Прямая на плоскости однозначно задается точкой и вектором, перпендикулярным к этой прямой. Такой вектор называется нормальным вектором. Пусть М 0(x 0, y 0) –точка, лежащая на прямой L; а вектор – нормальный вектор прямой L. Тогда для любой точки М(x, y), лежащей на этой прямой, вектор будет перпендикулярен вектору , а значит, их скалярное произведение должно быть равно нулю: 3

A(x – x 0)+B( y – y 0) = 0 − получили уравнение прямой, проходящей через точку M 0(x 0, y 0) перпендикулярно вектору 2. Выведем из полученного выше уравнения общее уравнение прямой: Пусть A(x – x 0)+B( y – y 0) =0. Раскроем скобки: Ax+By+(−A x 0−B y 0) = 0. Обозначим (–Ax 0 – By 0) = C, тогда получаем Ax + By + C = 0 – общее уравнение прямой на плоскости, где коэффициенты А, В - координаты нормального вектора. 4

3. Если С 0, то можно из общего уравнения прямой Ax + By + С = 0 получить уравнение прямой «в отрезках» . Разделим общее уравнение Ax + By = –С на коэффициент (–С): Обозначим: тогда уравнение прямой в отрезках, где a и b – величины направленных отрезков, отсекаемых прямой от координатных осей. 5

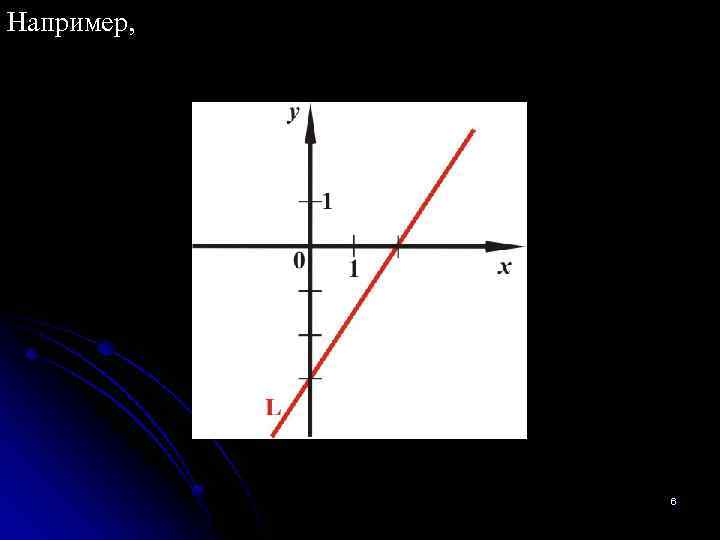Например, 6

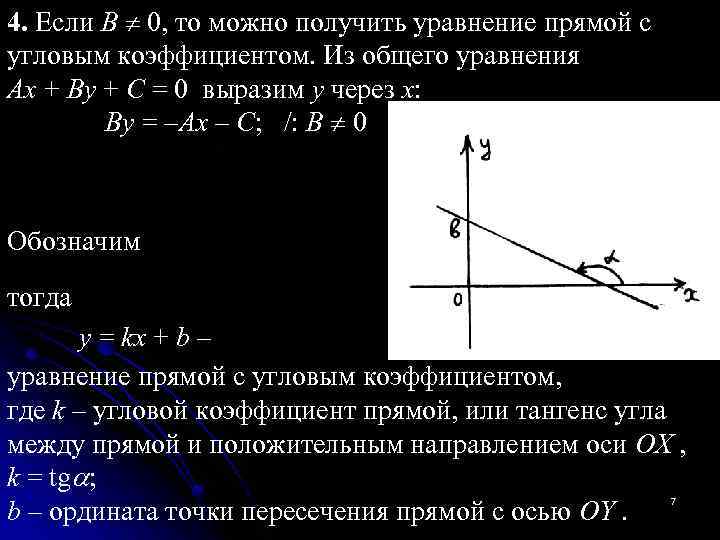4. Если В 0, то можно получить уравнение прямой с угловым коэффициентом. Из общего уравнения Ax + By + C = 0 выразим y через x: By = –Ax – C; /: В 0 Обозначим тогда y = kx + b – уравнение прямой с угловым коэффициентом, где k – угловой коэффициент прямой, или тангенс угла между прямой и положительным направлением оси ОХ , k = tg ; b – ордината точки пересечения прямой с осью OY. 7

Если угол - острый угол, то k>0, если угол - тупой , то k<0, если =0 прямая параллельна оси ОХ и k=0, если = / 2, то прямая не имеет углового коэффициента. 5. Прямая на плоскости так же однозначно задается точкой и вектором, параллельным этой прямой. Такой вектор называется направляющим. Пусть М 0(x 0, y 0) – точка, лежащая на прямой L; а вектор – направляющий вектор этой прямой. Тогда для любой точки М(x, y), лежащей на этой прямой, вектор будет коллинеарен вектору , а следовательно, координаты векторов будут пропорциональны: 8

получили каноническое уравнение прямой, проходящей через точку М(x 0, y 0) параллельно направляющему вектору 6. Получим из канонического уравнения прямой параметрическое уравнение, введя параметр t: параметрическое уравнение прямой, проходящей через точку М(x 0, y 0) параллельно вектору 9

7. Из параметрического уравнения получим уравнение прямой в векторном виде. Пусть радиус-вектор произвольной точки M, лежащей на прямой, радиус-вектор фиксированной точки M 0, лежащей на прямой, направляющий вектор, - уравнение прямой в векторном виде. 10

8. Найдем уравнение прямой L, проходящей через 2 точки А(x 1, y 1) и B(x 2, y 2) на плоскости. Тогда –направляющий вектор этой прямой, а точка A(x 1, y 1) L. Для любой точки М(x, y), лежащей на B прямой L, векторы и B должны быть А коллинеарны, а значит, их координаты должны быть пропорциональны: получили уравнение прямой, проходящей через точки A и B. 11

9. Нормальное уравнение прямой. Пусть р − расстояние от прямой до начала координат, α − угол, образуемый перпендикуляром к прямой и положительным направлением оси ОХ. Точка M(x, y) - произвольная точка , лежащая на прямой. Через начало координат проведем прямую перпендикулярно к данной. Точка P − точка пересечения этих прямых 12

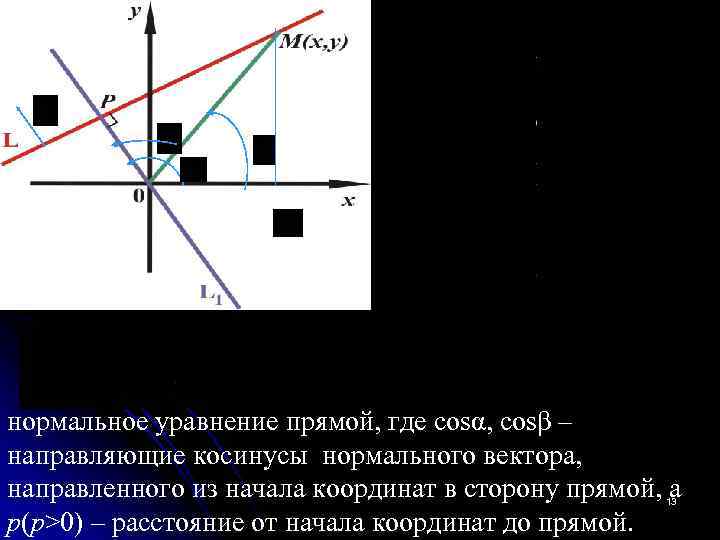нормальное уравнение прямой, где cosα, cosβ – направляющие косинусы нормального вектора, направленного из начала координат в сторону прямой, а p(p>0) – расстояние от начала координат до прямой. 13

Приведение общего уравнения прямой к нормальному виду. Пусть Ax+By+C = 0 – общее уравнение прямой. Умножим его на некоторый множитель , чтобы уравнение прямой имело нормальный вид: μ ·Ax+ μ · By+ μ · C = 0, μ ·A = cos α; μ · B = sin α. Но cos 2α + sin 2α = 1. Из этого условия находим множитель : Знак перед дробью выбирается противоположным знаку С ( для того, чтобы произведение С было отрицательным). 14

Взаимное расположение прямых на плоскости Прямые на плоскости могут совпадать, пересекаться или быть параллельными. 1. Пусть на плоскости заданы общими уравнениями две прямые L 1 и L 2: L 1: A 1 x + B 1 y + С 1 = 0, L 2: A 2 x + B 2 y + С 2 = 0, где и − нормальные векторы прямых L 1 и L 2, соответственно. Прямые на плоскости совпадают или параллельны, если нормальные векторы этих прямых коллинеарные, а значит, координаты векторов должны быть пропорциональны L 2 L 1 15

Следовательно, прямые а) совпадают, если б) параллельны, если в) пересекаются, если 16

2. Пусть прямые L 1 и L 2 заданы каноническими уравнениями: Прямые на плоскости совпадают или параллельны, если их направляющие вектора L 2 коллинеарные, а значит, их координаты пропорциональны. Тогда, прямые: а) совпадают, если L 1 б) параллельны, если в) пересекаются, если 17

3. Если прямые L 1 и L 2 заданы уравнениями с угловым коэффициентом L 1: y=k 1 x+b 1, L 2: y = k 2 x + b 2, то эти прямые: а) совпадают, если k 1 = k 2 и b 1 = b 2; б) параллельны, если k 1 = k 2 и b 1 b 2; в) пересекаются, если k 1 k 2. 18

Угол между прямыми на плоскости 1. Пусть на плоскости заданы прямые L 1 и L 2 общими уравнениями: L 1: A 1 x + B 1 y + С 1 = 0; L 2: A 2 x + B 2 y + С 2 = 0. Тогда косинус наименьшего угла между двумя прямыми L 1 и L 2 на плоскости равен модулю косинуса угла между нормальными векторами этих прямых: В случае если прямые перпендикулярны, их нормальные векторы также перпендикулярны, а значит, скалярное произведение нормальных векторов должно быть равно нулю. 19

2. Если прямые L 1 и L 2 заданы каноническими уравнениями: то косинус наименьшего угла между прямыми L 1 и L 2 равен модулю косинуса угла между направляющими векторами этих прямых: 20

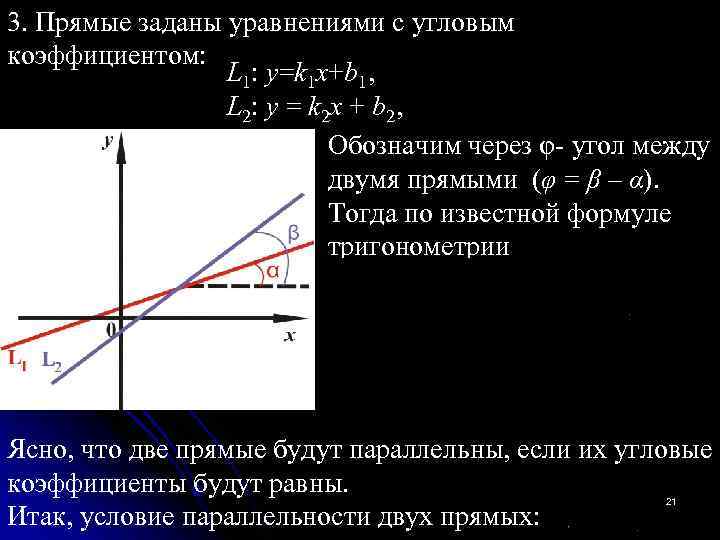3. Прямые заданы уравнениями с угловым коэффициентом: L 1: y=k 1 x+b 1, L 2: y = k 2 x + b 2, Обозначим через φ- угол между двумя прямыми (φ = β – α). Тогда по известной формуле тригонометрии Ясно, что две прямые будут параллельны, если их угловые коэффициенты будут равны. Итак, условие параллельности двух прямых: 21

Если две прямые перпендикулярны, т. е. угол φ = / 2, а значит, tg φ = tg ( / 2) = . Это будет иметь место, когда 1+k 1 k 2 = 0, т. е. k 1 k 2 = − 1. Итак, условие перпендикулярности двух прямых: k 1 k 2 = − 1. 22

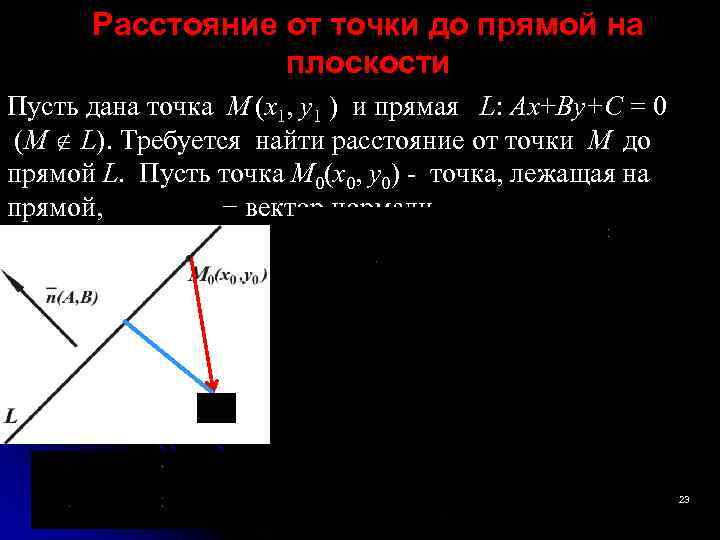Расстояние от точки до прямой на плоскости Пусть дана точка М (x 1, y 1 ) и прямая L: Ax+By+C = 0 (M L). Требуется найти расстояние от точки М до прямой L. Пусть точка М 0(x 0, y 0) - точка, лежащая на прямой, − вектор нормали. 23

Окончательно, получаем формулу для вычисления расстояния от точки до прямой Замечание. Расстояние между двумя параллельными прямыми на плоскости можно найти по последней формуле, если находить расстояние от любой точки, принадлежащей одной прямой, до другой прямой. 24

Плоскость в пространстве. Плоскость 25

В декартовых координатах каждая плоскость определяется уравнением первой степени Ax+By+Cz+D=0 и обратно, каждое уравнение первой степени Ax+By+Cz+D=0 определяет некоторую плоскость. Поверхности, которые в декартовых координатах определяются уравнениями первой степени, называются алгебраическими поверхностями первого порядка. Следовательно, каждая плоскость есть алгебраическая поверхность первого порядка; и каждая поверхность первого порядка есть плоскость. 26

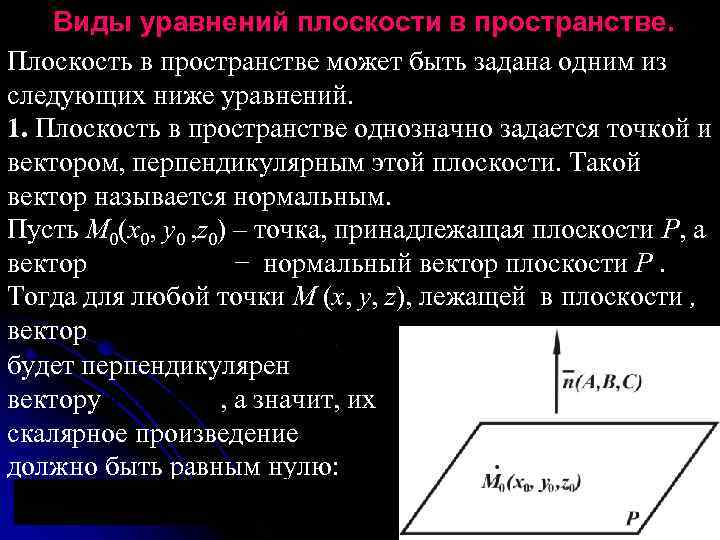Виды уравнений плоскости в пространстве. Плоскость в пространстве может быть задана одним из следующих ниже уравнений. 1. Плоскость в пространстве однозначно задается точкой и вектором, перпендикулярным этой плоскости. Такой вектор называется нормальным. Пусть М 0(x 0, y 0 , z 0) – точка, принадлежащая плоскости Р, а вектор − нормальный вектор плоскости Р. Тогда для любой точки М (x, y, z), лежащей в плоскости , вектор будет перпендикулярен вектору , а значит, их скалярное произведение должно быть равным нулю: 27

получили уравнение плоскости, проходящей через точку M 0(x 0, y 0, z 0) перпендикулярно вектору 2. Выведем из полученного выше уравнения общее уравнение плоскости: Обозначим , тогда получаем общее уравнение плоскости, где коэффициенты А, В и С - координаты вектора нормали. 28

3. Если D 0, можно получить уравнение плоскости «в отрезках» из общего уравнения плоскости разделив его на (–D): Обозначим , тогда получаем уравнение плоскости в «отрезках» : где a, b, c – величины направленных отрезков, отсекаемых плоскостью от координатных осей. 29

4. Нормальное уравнение плоскости. Пусть требуется написать уравнение плоскости P, если расстояние от начала координат до этой плоскости равно р, Через начало координат проведем прямую перпендикулярную плоскости. Вектор вектор нормали плоскости P. Точка K- точка пересечения прямой и плоскости. Пусть точка K M(x, y, z) − произвольная точка , лежащая в плоскости P. 30

Вектор тогда − направляющие косинусы нормали к плоскости. Следовательно, получили нормальное уравнение плоскости , где направляющие косинусы вектора нормали, направленного из начала координат в сторону плоскости, а p (p 0)– расстояние от начала координат до плоскости. 31

5. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой. Пусть A(x 1, y 1, z 1), B(x 2, y 2, z 2), C(x 3, y 3, z 3) Р. Тогда для любой точки М Р, векторы должны быть компланарны, а значит, их смешанное произведение равно нулю. Тогда смешанное произведение : Раскрыв, данный определитель по элементам первой строки, получим уравнении плоскости, проходящей через три заданные точки. 32

6. Уравнение плоскости, проходящей через заданную точку параллельно двум векторам. Пусть плоскость Р проходит через точку A(x 0, y 0, z 0) параллельно векторам и Тогда для любой точки М, принадлежащей плоскости Р, векторы должны быть компланарны, а значит, их смешанное произведение должно быть равно нулю. тогда: Раскрыв, данный определитель по элементам первой строки, получим уравнении плоскости, проходящей через заданную точку параллельно двум векторам. 33

7. Параметрическое уравнение плоскости. Пусть плоскость Р проходит через точку A(x 0, y 0, z 0) параллельно векторам и ( не коллинеарны). Так как векторы компланарны, то можно считать, что вектор может быть представлен в виде линейной комбинации векторов 34

8. Из параметрического уравнения получим уравнение плоскости в векторном виде. Обозначим : радиус-вектор произвольной точки M, лежащей в плоскости, радиус-вектор фиксированной точки M 0, лежащей в плоскости, векторы параллельные плоскости. Тогда 35

Взаимное расположение плоскостей Пусть в пространстве заданы две плоскости P 1 и P 2: где и – нормальные векторы плоскостей P 1 и P 2, соответственно. Плоскости в пространстве могут совпадать, быть параллельными или пересекаться. Плоскости совпадают или параллельны, если их нормальные векторы коллинеарны, а значит, координаты нормальных векторов должны быть пропорциональны, то есть Плоскости совпадают, если 36

Подставим в первое уравнение: Вычтем из первого уравнения второе, умноженное на k: Следовательно, плоскости: 1) совпадают, если 2) параллельны, если 3) пересекаются, если или 37

Приведение общего уравнения плоскости к нормальному виду. Пусть Ax+By+Cz+D=0 – общее уравнение плоскости. Умножим его на некоторый множитель μ, так чтобы уравнение плоскости имело нормальный вид: Но Из этого условия находим множитель μ: Знак перед дробью выбирается противоположным знаку D ( для того, чтобы μD было отрицательным). 38

Угол между плоскостями Пусть заданы две плоскости P 1 и P 2 где и – нормальные векторы плоскостей P 1 и P 2, соответственно. Косинус наименьшего двугранного угла между плоскостями Р 1 и Р 2 равен модулю косинуса угла между нормальными векторами этих плоскостей: 39

Расстояние от точки до плоскости. Пусть дана точка М 1(x 1, y 1, z 1) и плоскость P: Ax+By+Cz+D=0. Найдем расстояние d от точки М 1 до плоскости P. М 1 40

Точка М 0(x 0, y 0, z 0) лежит в плоскости P, а значит, ее координаты удовлетворяют уравнению плоскости, то есть Ax 0+By 0+Cz 0+D=0 - Ax 0 - By 0 - Cz 0=D. Окончательно, получаем формулу для расстояния от точки до плоскости Замечания. 1. Расстояние между двумя параллельными плоскостями можно найти по той же формуле, если находить расстояние от любой точки, принадлежащей одной плоскости, до другой плоскости. 2. Если задано нормальное уравнение плоскости то 41

Прямая в пространстве. 42

Уравнения прямой в пространстве. Прямая в пространстве может быть задана одним из следующих ниже уравнений. 1. Общее уравнение прямой. Прямая в пространстве может быть задана как линия пересечения двух непараллельных плоскостей: где коэффициенты А 1, В 1, С 1 не пропорциональны коэффициентам А 2, В 2, С 2. Это общее уравнение прямой в пространстве. Замечание. Через каждую прямую проходит бесконечное множество различных плоскостей. Значит, существует бесконечно много возможностей выбрать две из них. 43

2. Прямая в пространстве однозначно задается точкой M 0(x 0, y 0, z 0), лежащей на этой прямой, и вектором , параллельным этой прямой. Такой вектор называется направляющим. Для любой точки М(x, y, z), лежащей на прямой L, вектор коллинеарен вектору , а значит, координаты этих векторов должны быть пропорциональны. - каноническое уравнение прямой, проходящей через точку М 0(x 0, y 0, z 0) параллельно направляющему вектору 44

3. Из канонического уравнения прямой получим параметрическое уравнение, введя параметр t (– , ): параметрическое уравнение прямой, проходящей через точку М 0(x 0, y 0, z 0) параллельно направляющему вектору 45

4. Уравнение прямой в векторном виде. Обозначим : радиус-вектор произвольной точки M, лежащей на прямой, радиус-вектор фиксированной точки M 0, лежащей на прямой, направляющий вектор прямой, тогда 46

Связь между общим уравнением прямой и каноническим. Пусть задано общее уравнение прямой: Чтобы перейти от общего уравнения прямой к каноническому уравнению нужно найти какую-нибудь точку , лежащую на прямой и направляющий вектор Координаты точки на прямой получим из системы уравнений, придав одной из координат произвольное значение. Так как прямая перпендикулярна нормальным векторам и , то за направляющий вектор прямой можно принять векторное произведение 47

Пример. Найти каноническое уравнение прямой Решение Первый способ: Найдем координаты точки М 0. , лежащей на прямой. Для этого мы можем одну из координат, например z 0, взять равной нулю. Пусть точка M 0(x 0, y 0, 0) L, тогда: 48

Найдем координаты направляющего вектора . (1, – 1, 4) – нормальный вектор плоскости Р 1; – нормальный вектор плоскости Р 2. Направляющий вектор прямой перпендикулярен векторам и , следовательно, он коллинеарен вектору векторного произведения векторов и. 49

Итак, вектор (3, 11, 2) - направляющий вектор прямой L; а точка , отсюда получаем каноническое уравнение прямой L: Второй способ: Пусть Выразим из второго уравнения и подставим его в первое уравнение: 50

Третий способ. Найдем координаты двух точек, лежащих на данной прямой. Координаты точки были найдены ранее. Найдем координаты еще одной точки, лежащей на прямой Пусть, например, x 1=0. Тогда 51

Найдем координаты вектора Тогда в качестве направляющего вектора прямой мы можем взять любой вектор, коллинеарный вектору Например, можем взять вектор (3, 11, 2). Тогда каноническое уравнение прямой: 52

Взаимное расположение прямых в пространстве. Прямые в пространстве могут совпадать, быть параллельными, пересекаться или скрещиваться. Две прямые L 1 и L 2 лежат в одной плоскости тогда и только тогда, когда компланарны векторы , где – направляющие векторы прямых L 1 и L 2, соответственно, а - вектор, соединяющий произвольную точку М 1, лежащую на прямой L 1, с точкой М 2, лежащей на прямой L 2. Следовательно, если смешанное произведение векторов равно нулю, то прямые лежат в одной плоскости. Если прямые принадлежат одной плоскости, то они могут совпадать, пересекаться и быть параллельными. 53

Пусть заданы прямые L 1 и L 2: где М 1(x 1, y 1, z 1) L 1 , М 2(x 2, y 2, z 2) L 2, а (l 1, m 1, n 1) и (l 2, m 2, n 2) – направляющие векторы прямых L 1 и L 2, соответственно: Тогда прямые L 1 и L 2: 1) скрещиваются, если 54

2) пересекаются, если и вектор не коллинеарен вектору , т. е. координаты этих векторов не пропорциональны: или 3) параллельны, если и точка М 1(x 1, y 1, z 1) L 2, то есть 55

4) совпадают, если и точка М 1(x 1, y 1, z 1) L 2, то есть 56

Угол между прямыми в пространстве Пусть где (l 1, m 1, n 1) и (l 2, m 2, n 2) – направляющие векторы прямых L 1 и L 2. При пересечении прямые образуют 4 угла (две пары смежных углов. ) Наименьший из двух смежных углов в паре – угол между прямыми. L 2 L 1 57

Косинус наименьшего угла между прямыми L 1 и L 2 равен модулю косинуса угла между направляющими векторами этих прямых: 58

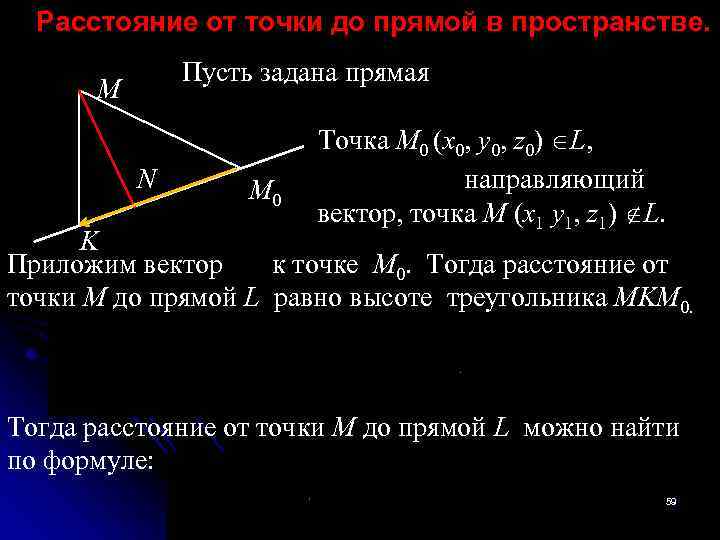Расстояние от точки до прямой в пространстве. Пусть задана прямая M Точка M 0 (x 0, y 0, z 0) L, N M 0 направляющий вектор, точка M (x 1 y 1, z 1) L. K Приложим вектор к точке M 0. Тогда расстояние от точки М до прямой L равно высоте треугольника MKM 0. Тогда расстояние от точки М до прямой L можно найти по формуле: 59

Замечание. Расстояние между параллельными прямыми может быть найдено по этой же формуле, как расстояние от любой точки, принадлежащей одной прямой, до другой прямой. 60

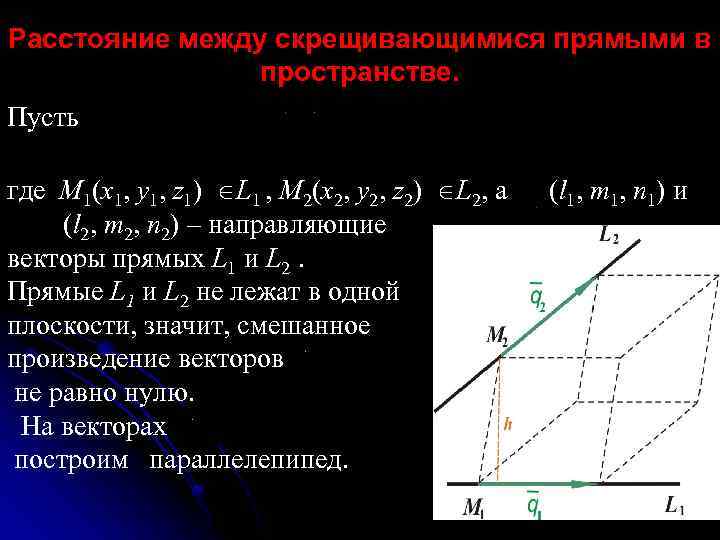Расстояние между скрещивающимися прямыми в пространстве. Пусть где М 1(x 1, y 1, z 1) L 1 , М 2(x 2, y 2, z 2) L 2, а (l 1, m 1, n 1) и (l 2, m 2, n 2) – направляющие векторы прямых L 1 и L 2. Прямые L 1 и L 2 не лежат в одной плоскости, значит, смешанное произведение векторов не равно нулю. На векторах построим параллелепипед. 61

Тогда расстояние между скрещивающимися прямыми можно найти по формуле: где – модуль смешанного произведения векторов - длина векторного произведения 62

Взаимное расположение прямой и плоскости в пространстве. Пусть в пространстве заданы прямая и плоскость Точка , вектор (l, m, n) – направляющий вектор прямой L; вектор (А, В, С) – нормальный вектор плоскости Р. Прямая может пересекать плоскость, быть ей параллельной или лежать в плоскости. 1. Если прямая лежит в плоскости, то и точка М(x 0, y 0, z 0) P. Таким образом, прямая лежит в плоскости, если: Al + Bm + Cn = 0 и 63

2. Если прямая параллельна плоскости, то и точка М(x 0, y 0, z 0) P. Таким образом, прямая параллельна плоскости, если: Al + Bm + Cn = 0 и P 3. Прямая пересекает плоскость, если направляющий вектор прямой не перпендикулярен нормальному вектору плоскости, а значит их скалярное произведение не равно нулю: , т. е. Al + Bm + Cn 0. P 64

Угол между прямой и плоскостью. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость. Рассмотрим прямую и плоскость если угол β острый, если угол β тупой. 65

66