Прямая линия в пространстве Прямая линия

Прямая линия в пространстве

Прямая линия Способы графического задания прямой

Способы задания прямой на эпюре: Проекциями двух Проекцией точки принадлежащих ей точек и направлением В 2 b 2 И А 2 X А 1 А 1 b 1 И В 1 Эпюром прямой называется чертеж, состоящий из двух или более ортогональных проекций, связанных между собой

Способы задания прямой в пространстве: Двумя ее проекциями B 2 B A 2 0 A B 1 A 1

Задание и изображение прямой на комплексном ортогональном чертеже Прямая есть такое множество точек, свойства которого определяются известной аксиомой прямой линии: «через любые две различные точки проходит одна и только одна прямая» и теоремой, которая следует из аксиомы прямой: «две различные прямые могут иметь не более одной общей точки". По расположению относительно плоскостей проекций прямые могут быть общего и частного положений. Прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется прямой общего положения.

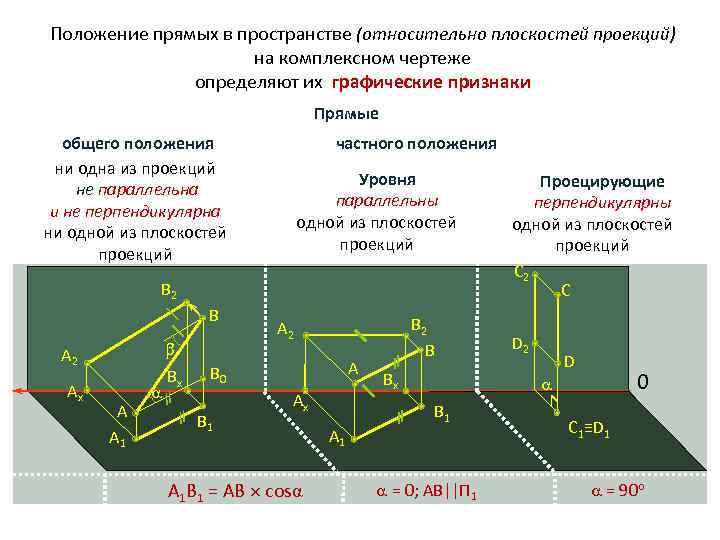Положение прямых в пространстве (относительно плоскостей проекций) на комплексном чертеже определяют их графические признаки Прямые общего положения частного положения ни одна из проекций Уровня Проецирующие не параллельна параллельны перпендикулярны и не перпендикулярна одной из плоскостей ни одной из плоскостей проекций C 2 B 2 C B A 2 B D 2 A 2 D Вx B 0 A Ax Вx 0 Ax A B 1 C 1≡D 1 A 1 А 1 В 1 = АВ cosα = 0; АВ||П 1 = 90 o

Пj Линией уровня называется A линия, параллельная одной z Aj из плоскостей проекций Ai A i, j z Линия уровня и плоскость, // j /// которой она параллельна, /// B имеют одинаковые названия j Bj /// z М j (имена) пп z М Bi j B i, j z п Пi Мi Метрические свойства: Xi, j Длина одноименной проекции отрезка прямой равна длине самого отрезка [АВ] = [Аi. Вi], а угол оj наклона одноименной проекции отрезка [Аi. Вi] к оси хi, j равен углу о наклона самого отрезка [АВ] к разноименной плоскости проекций j

h – горизонталь z(х2, 3) Z(х2, 3) h 2 h 3 h 2 h 3 Zh Zh П 2 П 3 Х 1, 2 П 1 Y(х1, 3) y(х x 1, 2 h 1 1 , 3 ) h 1= нв h 2 3 Y(х1, 3)

f – фронталь z(х2, 3) Z(х2, 3) f 2 П 2 // f 3 П 3 yf f f 3 нв // f 2 = 3 1 yf Х 1, 2 П 2 П 3 Y(х1, 3) П 1 y(х yf x 1, 2 f 1 1 , 3 ) f 1 П 1 Y(х1, 3)

р – профильная прямая z(х2, 3) Z(Х 2, 3) хр yр р 3= р2 3 нв р3 р3 р2 р хр yf 1 П 2 П 3 Х 1, 2 П 1 yр хр Y(Х 1, 3) x 1, 2 y(х 1 , 3 ) р1 хр Y(Х 1, 3)

z(х2, 3) Проецирующей называется прямая, перпендикулярная nj какой-либо плоскости ni проекций: n Пi в пространстве одноименная проекция проецирующей прямой вырождается в точку, y(х x 1, 2 1 , 3 ) а разноименная – перпендикулярна оси, nq разделяющей ее с одноименной проекцией

Z(Х 2, 3) а – горизонтально проецирующая прямая а 2 а 3 в – фронтально c 2 c 3 проецирующая прямая b 2 b 3 П 2 П 3 с – профильно Х 1, 2 проецирующая прямая П 1 Y(Х 1, 3) c 1 а 1 b 1 Y(Х 1, 3)

Так как две точки однозначно определяют положение прямой в пространстве, то достаточно задать на комплексном чертеже проекции двух точек, принадлежащих прямой и попарно соединить их первые, вторые и третьи проекции.

Комплексный чертеж прямой общего положения

Прямая частного положения (или прямая уровня) – прямая, параллельная хотя бы одной из плоскостей проекций. Прямая, параллельная горизонтальной плоскости проекций, называется горизонталью - h. На горизонтальную плоскость проекций горизонталь проецируется в натуральную величину. Графический признак горизонтали – z=const.

Прямая, параллельная фронтальной плоскости проекций, называется фронталью - f. На фронтальную плоскость проекций фронталь проецируется в натуральную величину. Графический признак фронтали – y=const.

Прямая, параллельная профильной плоскости проекций, называется профильной прямой - р. На профильную плоскость проекций профильная прямая проецируется в натуральную величину.

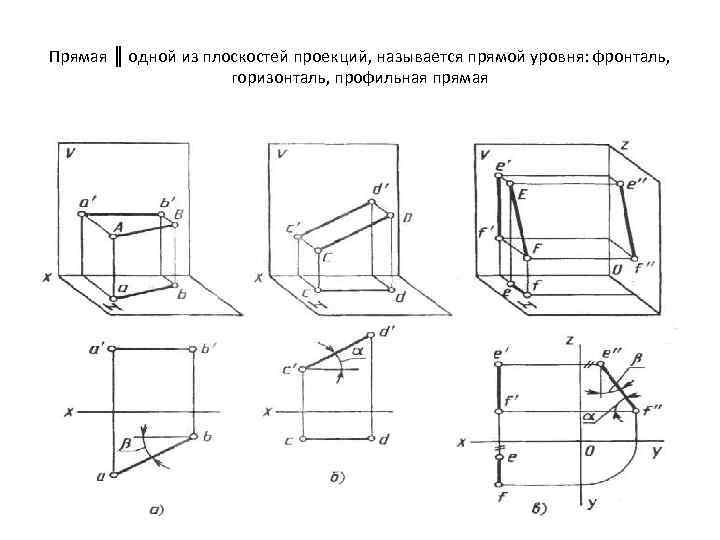Прямая ║ одной из плоскостей проекций, называется прямой уровня: фронталь, горизонталь, профильная прямая

• Прямые, перпендикулярные к плоскостям проекций называются проецирующими. • Прямая, перпендикулярная к горизонтальной плоскости проекций, называется горизонтально- проецирующей. • Прямая, перпендикулярная к фронтальной плоскости проекций, называется фронтально- проецирующей. • Прямая, перпендикулярная к профильной плоскости проекций, называется профильно- проецирующей.

Прямая называется проецирующей, если она перпендикулярна одной из плоскостей проекций. Одна из проекций такой прямой есть точка. Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций. Горизонтальной проекцией такой прямой является точка, а фронтальная и профильная проекции || оси z.

Фронтально проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций. Фронтальной проекцией такой прямой является точка, а горизонтальная и профильная проекции || оси y.

Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций. Профильной проекцией такой прямой является точка, а горизонтальная и фронтальная проекции || оси x.

Прямые частного положения: 1)- Прямые ┴ одной из плоскостей проекций; 2)- прямые ║ одной из плоскостей проекций. Прямая ┴ одной из плоскостей проекций называется проецирующей прямой

Следы прямой Следом прямой линии называется точка в которой прямая пересекается с плоскостью проекций. Горизонтальный след - точка пересечения прямой с горизонтальной плоскостью проекций. Фронтальный след - точка пересечения прямой с фронтальной плоскостью проекций. Профильный след - точка пересечения прямой с профильной плоскостью проекций. Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с самим следом, а другие проекции лежат на осях.

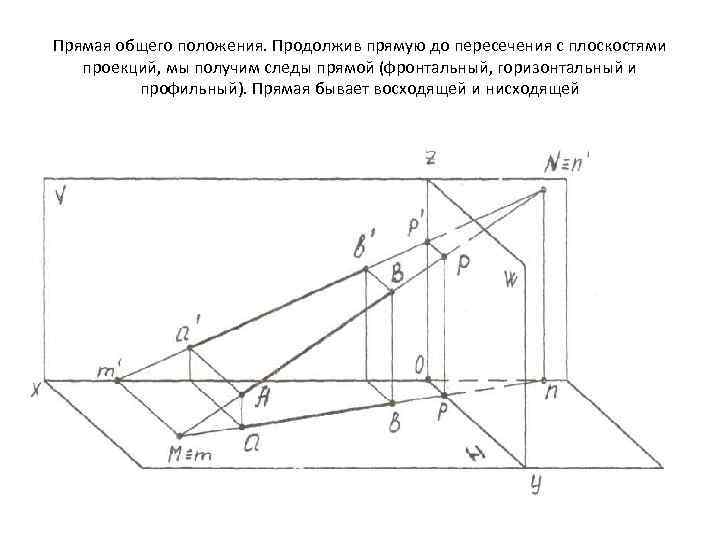Прямая общего положения. Продолжив прямую до пересечения с плоскостями проекций, мы получим следы прямой (фронтальный, горизонтальный и профильный). Прямая бывает восходящей и нисходящей

1. Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью 0 x и в этой точке восстановить перпендикуляр к оси до пересечения с горизонтальной проекцией прямой. 2. Для построения фронтального следа N прямой нужно из точки пересечения горизонтальной проекции её с осью 0 x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой. Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.

Две прямые в пространстве могут занимать следующее положение: быть взаимно параллельными, пересекаться, скрещиваться, быть взаимно перпендикулярными.

Параллельные прямые Согласно свойству параллельного проецирования одноименные проекции двух параллельных прямых линий параллельны, находятся в таком же отношении, как и длины самих отрезков и являются проекциями одного направления. Для определения по проекциям прямых их взаимного положения в пространстве для прямых общего положения достаточно двух проекций этих прямых.

Если в пространстве прямые параллельны, то их одноименные проекции параллельны

Параллельные прямые Графический признак параллельности прямых: если одноименные проекции прямых на каждой из плоскостей проекций параллельны между собой, то и сами прямые в пространстве параллельны между собой

Пересекающиеся прямые Прямые линии, имеющие общую точку, называются пересекающимися. Согласно свойству параллельного проецирования одноименные проекции этих прямых пересекаются и точки их пересечения являются проекциям одной точки пространства, т. е. принадлежат одной линии связи. Угол между пересекающимися прямыми общего положения не проецируется в натуральную величину ни на одну из плоскостей проекций.

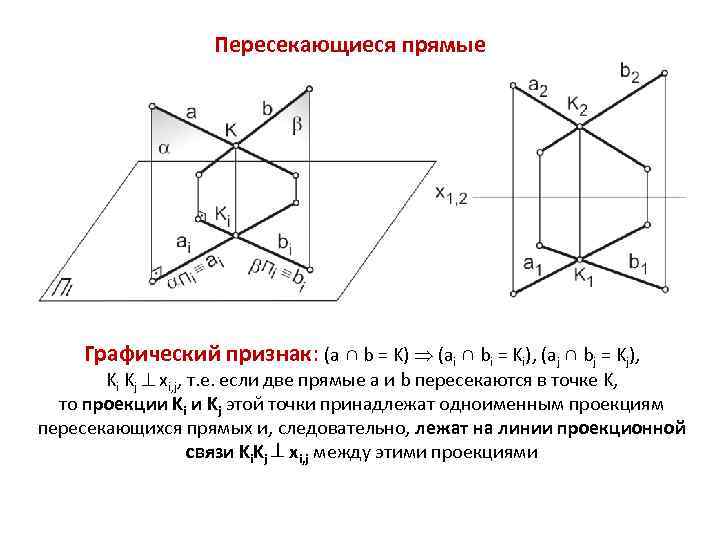Пересекающиеся прямые Графический признак: (a ∩ b = K) (ai ∩ bi = Ki), (aj ∩ bj = Kj), Ki Kj xi, j, т. е. если две прямые a и b пересекаются в точке K, то проекции Ki и Kj этой точки принадлежат одноименным проекциям пересекающихся прямых и, следовательно, лежат на линии проекционной связи Ki. Kj xi, j между этими проекциями

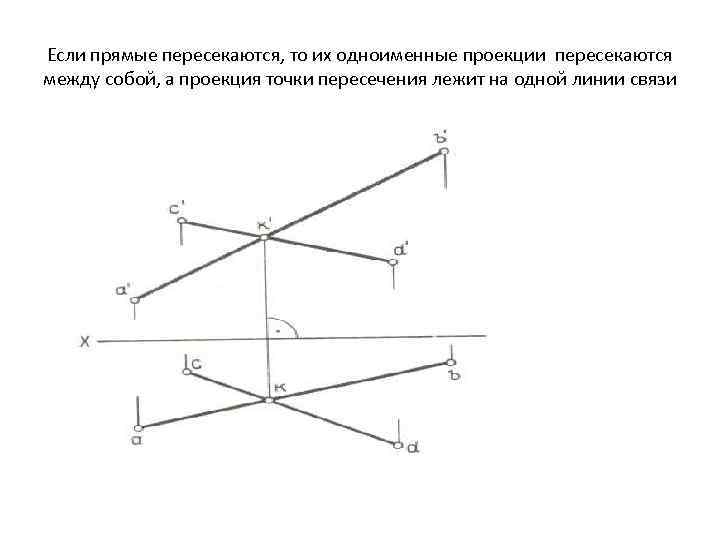Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекция точки пересечения лежит на одной линии связи

Скрещивающиеся прямые Прямые, не пересекающиеся и не параллельные между собой, называются скрещивающимися. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в параллельных плоскостях. Проекции двух скрещивающихся прямых могут пересекаться, но точки пересечения одноименных проекций не лежат на одной линии связи, т. е. каждая из точек пересечения проекций прямых является проекцией двух точек пространства, они лежат на одном проецирующем луче. Такие точки называются конкурирующими.

Скрещивающиеся прямые не имеют общих точек. Точки пересечения одноименных прямых не лежат на одной прямой

Скрещивающиеся прямые Графический признак скрещивающихся прямых: признак основан на невыполнении признаков параллельности или пересечения таких прямых. Точки пересечения одноименных проекций на смежных плоскостях не лежат на линии их проекционной связи, а параллельность проекций может иметь место только на одной из плоскостей проекций

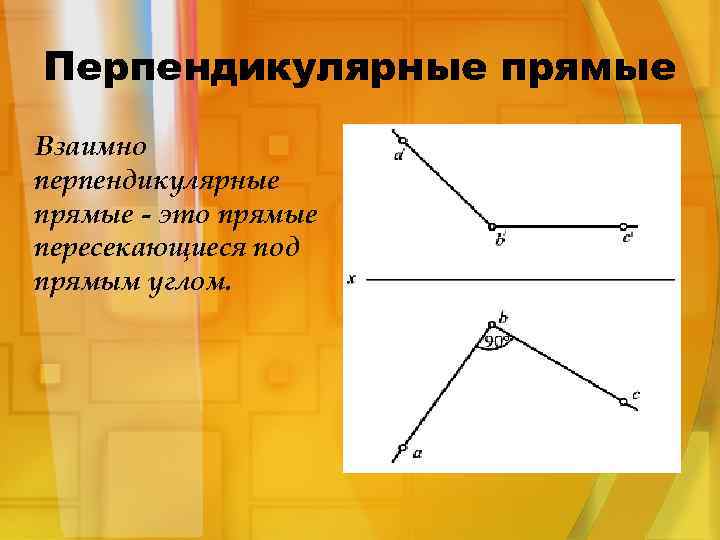Перпендикулярные прямые Взаимно перпендикулярные прямые - это прямые пересекающиеся под прямым углом.

Теорема о проецировании прямого угла Дано: АВ ВС; АВ ll Пi; ВС ll Пi Доказать, что Аi. Вi Вi. Сi Доказательство: С 1) АВ ВС и АВ ll Пi по условию теоремы; 2) АВ ВВi из условия n ортогонального проецирования ВВi Сi Пi В АВ (ВС∩ВВi) (ВССi. Вi); m ni А // Z 3) (АВ Аi. Вi) Z mi Аi. Вi (ВССi. Вi); // Вi Аi 4) (Вi. Сi (ВССi. Вi) Аi. Вi Вi. Сi , Пi что и требовалось доказать

Взаимное положение прямой и точки

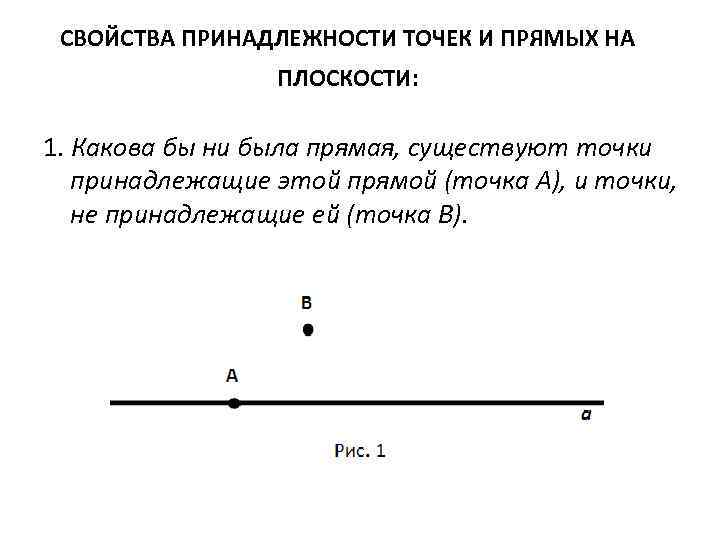СВОЙСТВА ПРИНАДЛЕЖНОСТИ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ: 1. Какова бы ни была прямая, существуют точки принадлежащие этой прямой (точка А), и точки, не принадлежащие ей (точка В).

СВОЙСТВА ПРИНАДЛЕЖНОСТИ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ: 2. Через любые две точки можно провести прямую, и только одну. 3. Если взять две несовпадающие точки (А и С), то через них можно провести только одну прямую (а), хотя через каждую из этих точек можно провести бесчисленное множество прямых. 4. Если точки А и С совпадают (на чертеже в этом случае одна точка будет обозначена двумя буквами), то через них можно провести бесчисленное множество прямых.

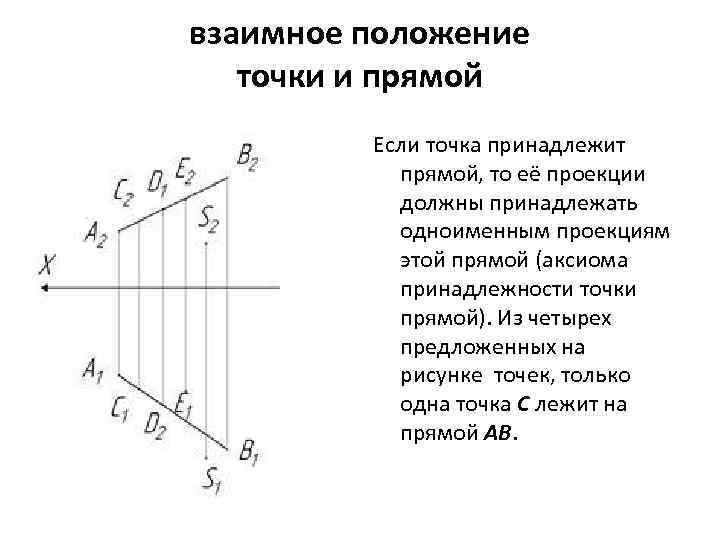взаимное положение точки и прямой Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке точек, только одна точка С лежит на прямой АВ.

взаимное положение точки и прямой В тех случаях когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П 1, П 2 и П 3), то вопрос о взаимном расположении прямой и точки решается при построении проекций на три плоскости проекций, тогда как для определения взаимного положения прямой и точки в других случаях достаточно построений на две плоскости проекции.

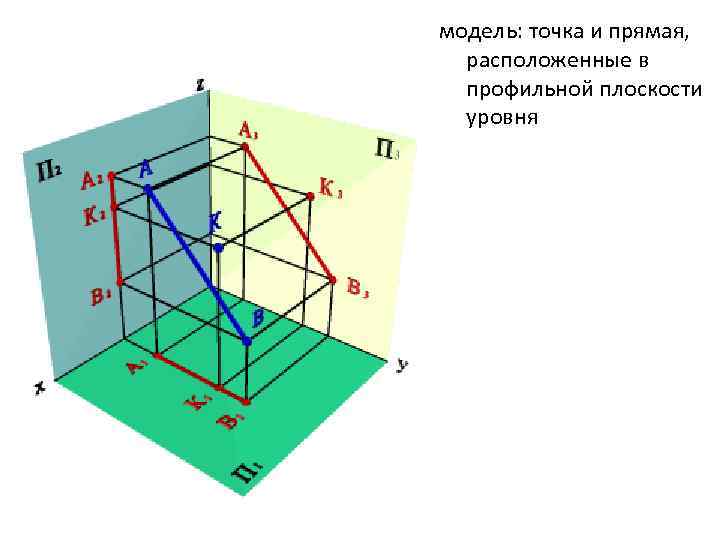модель: точка и прямая, расположенные в профильной плоскости уровня

Вопросы для повторения 1. Сколько проекций точки необходимо, чтобы определить ее положение в пространстве? 2. Что такое комплексный чертеж? 3. Что называется координатами точки? 4. Какой чертеж называется двухкартинным? 5. Как задается прямая на чертеже? 6. Что такое следы прямой? 7. Каким может быть взаимное положение двух прямых? 8. Каким может быть взаимное положение точки и прямой? 9. Сколько проекций точек необходимо, чтобы задать прямую на чертеже (эпюре? ) 10. Перечислите линии уровня и укажите их графические признаки. 11. Какие прямые называют проецирующими? Перечислите их графические признаки. 12. Как отличить на эпюре пересекающиеся прямые от скрещивающихся?