Прямая линия Прямая в пространстве бесконечна и непрерывна

Прямая линия Прямая в пространстве бесконечна и непрерывна. Ограниченная часть прямой называется отрезком.

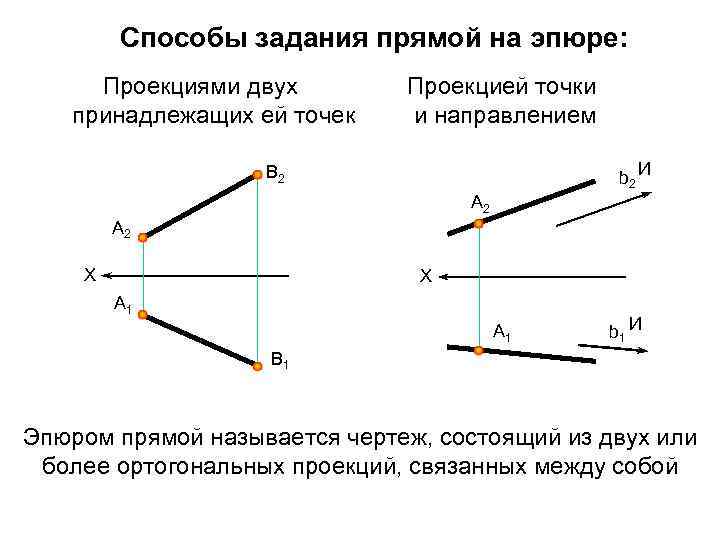
Способы задания прямой на эпюре: Проекциями двух принадлежащих ей точек Проекцией точки и направлением b 2 И В 2 А 2 X X А 1 b 1 И В 1 Эпюром прямой называется чертеж, состоящий из двух или более ортогональных проекций, связанных между собой

Определение длины отрезка прямой линии и углов наклона прямой к плоскостям проекций

Натуральная величина отрезка прямой Bi // // Способ прямоугольного треугольника Дано: [АВ] ; [Аi. Bi]; [Aj. Bj] Теорема: Натуральная величина отрезка B АВ есть гипотенуза Вj прямоугольного треугольника, у которого один катет есть его проекция, а другой катет - разность координат концов этого отрезка (взятый из другой проекции). i Пj A Aj Ai Пi j Xi, Угол между проекцией Аi. Вi и гипотенузой (натуральной величиной АВ ) равен углу оi наклона отрезка АВ к плоскости П i и к проекции Аi. Вi

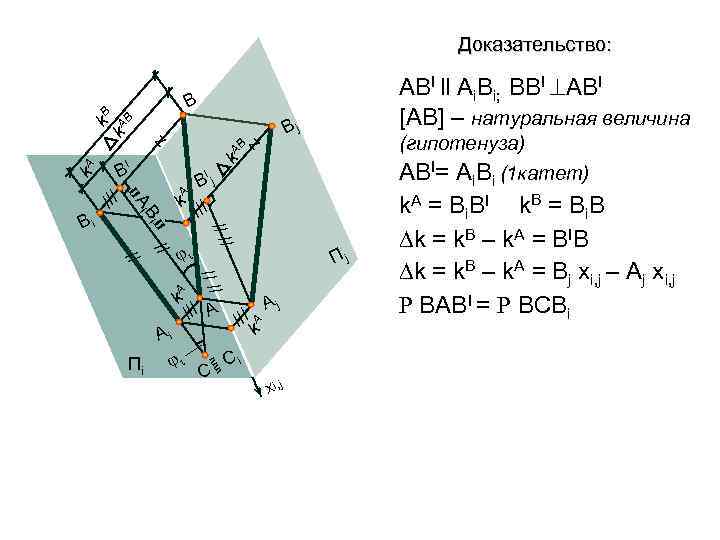
Доказательство: k AB z I Вj z (гипотенуза) АВI= Ai. Bi (1 катет) I Bj /// B i Пj // // k. A // // п // i /// Aj k. A B /// k. A k AB k. B B п. A Bi АВI ll Ai. Bi; BBI АВI [АВ] – натуральная величина п пп Ai Пi i C C i j Xi, k. A = Вi. ВI k. B = Вi. В k = k. B – k. A = ВIВ k = k. B – k. A = Вj хi, j – Aj хi, j Р ВАВI = Р ВСBi

[АВ] – натуральная величина (гипотенуза) нв АB A 0 B 2 z. AB A 2 х B 1 A 1 нв АB z. AB B 0 α - угол наклона отрезка АВ к плоскости П 1 и к проекции А 1 В 1 β - угол наклона отрезка АВ к плоскости П 2 и к проекции А 2 В 2

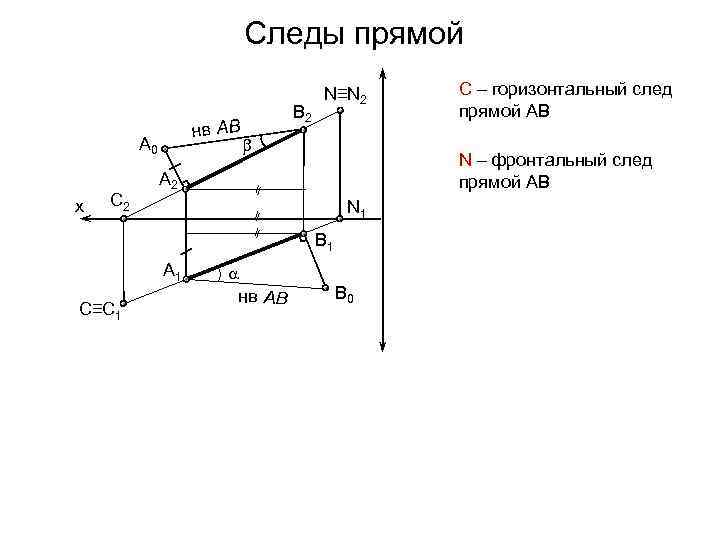
Следы прямой нв АB A 0 х C 2 B 2 N≡N 2 N – фронтальный след прямой АВ A 2 N 1 B 1 A 1 С≡С 1 нв АB С – горизонтальный след прямой АВ B 0

Положение прямой относительно плоскостей проекций

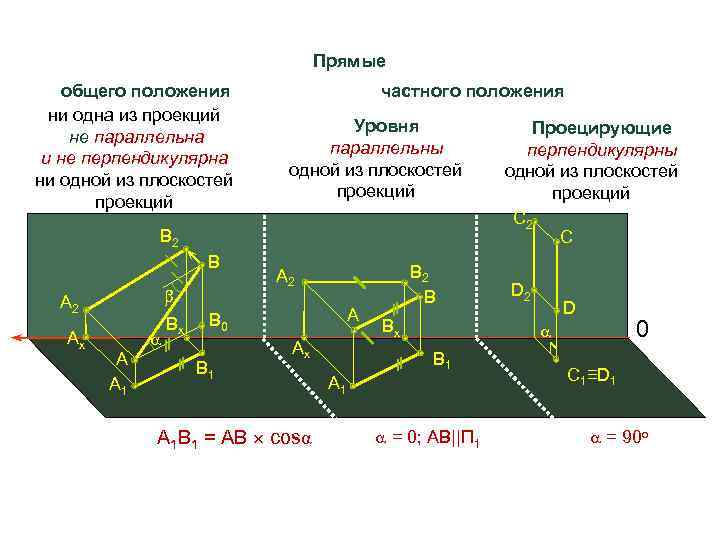
Прямые общего положения ни одна из проекций не параллельна и не перпендикулярна ни одной из плоскостей проекций частного положения Уровня параллельны одной из плоскостей проекций B 2 B A 2 Ax A A 1 Вx A B 0 B 1 B 2 B A 2 Ax А 1 В 1 = АВ cosα Вx Проецирующие перпендикулярны одной из плоскостей проекций C 2 C D 2 D 0 B 1 A 1 = 0; АВ||П 1 C 1≡D 1 = 90 o

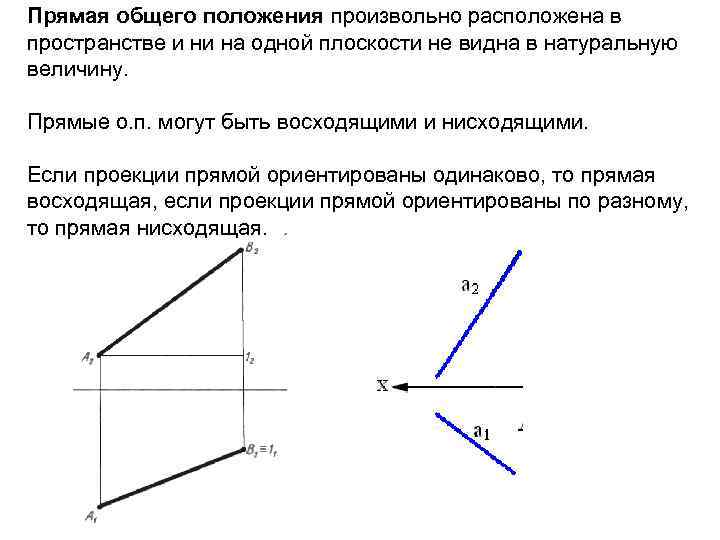
Прямая общего положения произвольно расположена в пространстве и ни на одной плоскости не видна в натуральную величину. Прямые о. п. могут быть восходящими и нисходящими. Если проекции прямой ориентированы одинаково, то прямая восходящая, если проекции прямой ориентированы по разному, то прямая нисходящая.

Линии уровня

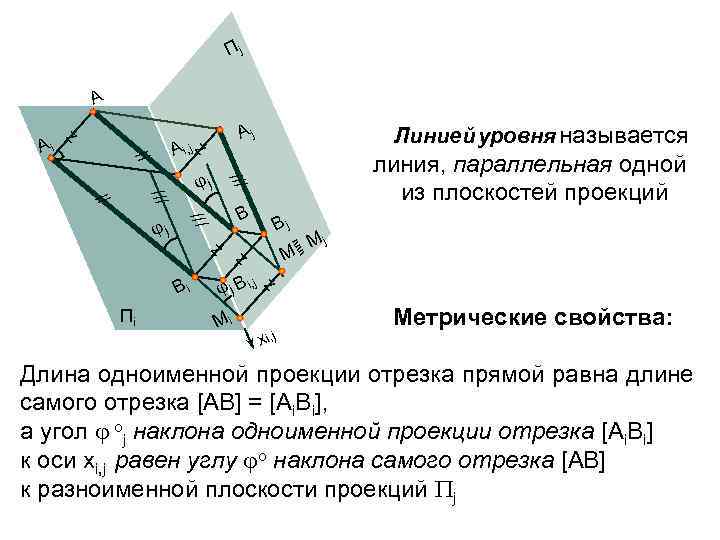
Пj A Aj Линией уровня называется j /// B линия, параллельная одной из плоскостей проекций /// z // Ai A i, j z /// // j Пi z j п Bi М М пп z Bj j B i, j z Мi j Xi, Метрические свойства: Длина одноименной проекции отрезка прямой равна длине самого отрезка [АВ] = [Аi. Вi], а угол оj наклона одноименной проекции отрезка [Аi. Вi] к оси хi, j равен углу о наклона самого отрезка [АВ] к разноименной плоскости проекций j

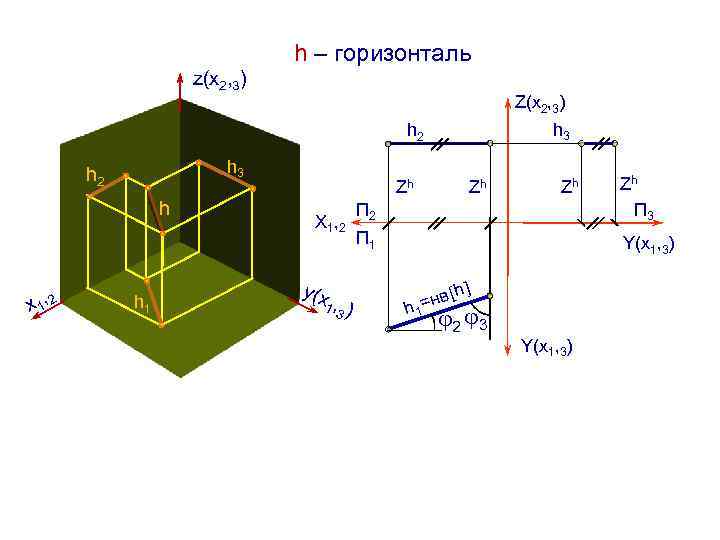
h – горизонталь z(х2, 3) Z(х2, 3) h 3 h 2 h x 1, 2 h 1 П 2 Zh П 3 П 1 Y(х1, 3) Zh Х 1 , 2 y(х 1 , 3 ) Zh нв h h 1= 2 3 Zh Y(х1, 3)

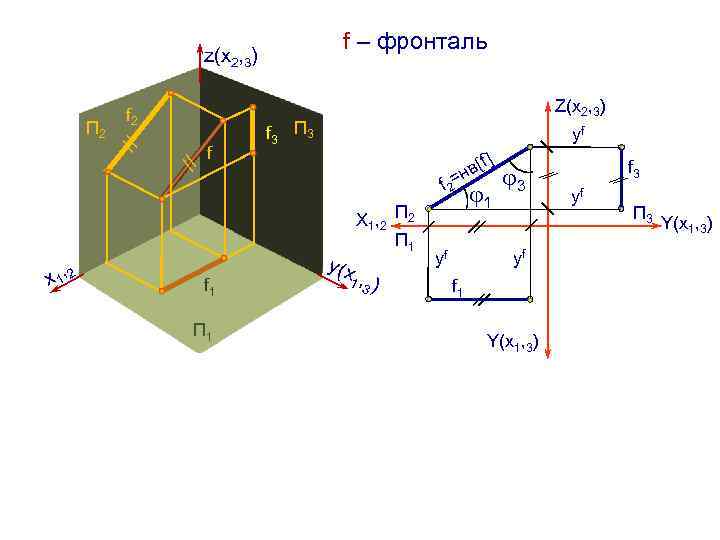
f – фронталь z(х2, 3) // // П 2 f 2 x 1, 2 f Z(х2, 3) f 3 П 3 yf f 2= f 1 П 1 y(х Х 1 , 2 П 1 1 , 3 ) в f н 1 3 yf yf f 1 Y(х1, 3) f 3 yf П 3 Y(х1, 3)

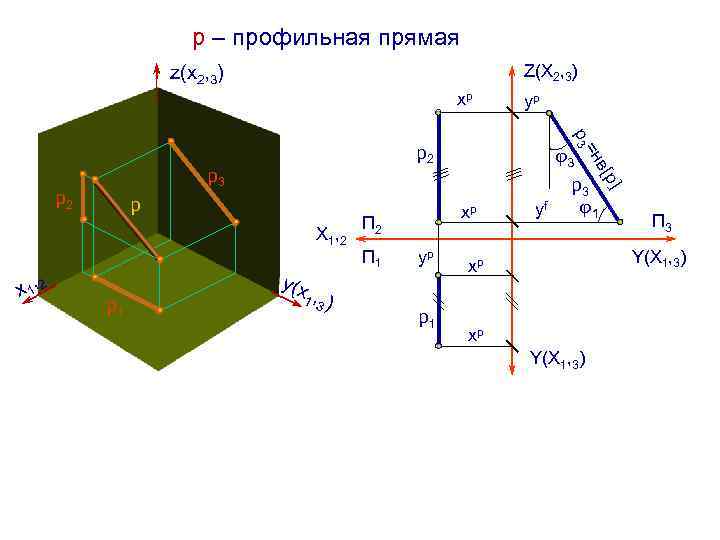
р – профильная прямая Z(Х 2, 3) z(х2, 3) хр 1 , 3 ) П 2 П 1 yр р1 yf 1 y(х хр в р р р1 =н р3 р3 Х 1 , 2 x 1, 2 3 р2 р3 р2 yр П 3 Y(Х 1, 3) хр хр Y(Х 1, 3)

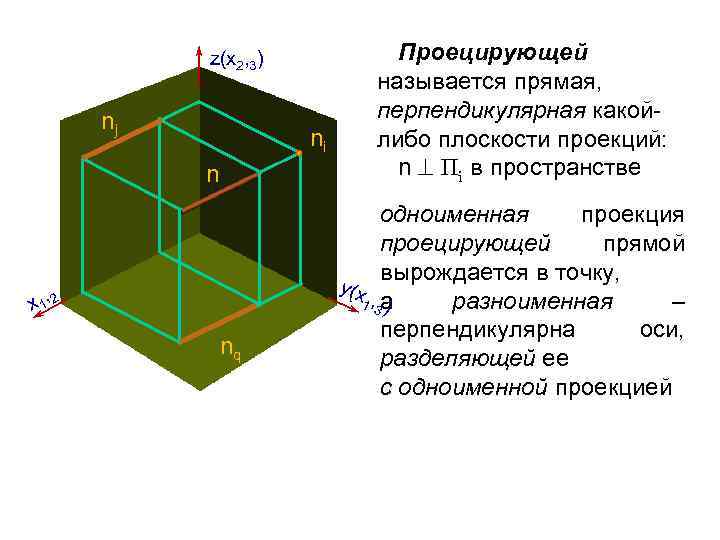
z(х2, 3) nj ni n x 1, 2 nq Проецирующей называется прямая, перпендикулярная какойлибо плоскости проекций: n Пi в пространстве одноименная проекция проецирующей прямой вырождается в точку, y(х 1 , 3 а разноименная – ) перпендикулярна оси, разделяющей ее с одноименной проекцией

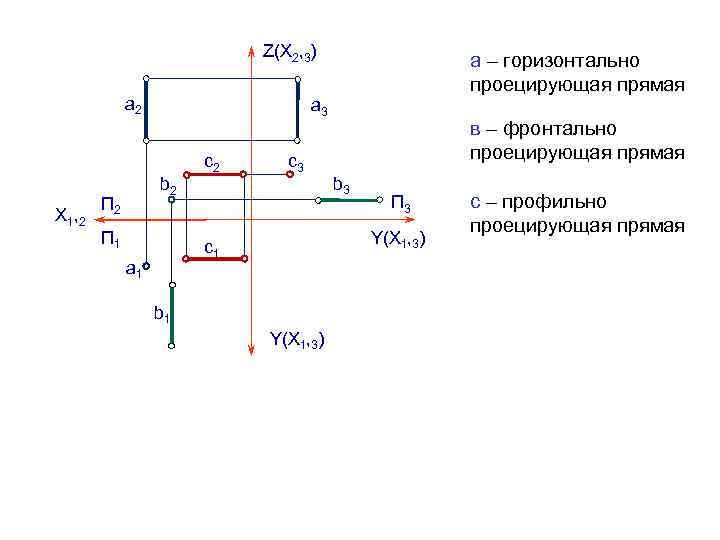
Z(Х 2, 3) а 2 Х 1 , 2 а 3 b 2 П 2 а – горизонтально проецирующая прямая П 1 c 2 c 3 b 3 П 3 Y(Х 1, 3) c 1 а 1 в – фронтально проецирующая прямая b 1 Y(Х 1, 3) с – профильно проецирующая прямая

Взаимное расположение двух прямых

Пересекающиеся прямые (a ∩ b = K) (ai ∩ bi = Ki), (aj ∩ bj = Kj), Ki Kj xi, j, т. е. если две прямые a и b пересекаются в точке K, то проекции Ki и Kj этой точки принадлежат одноименным проекциям пересекающихся прямых и лежат на линии проекционной связи Ki. Kj xi, j

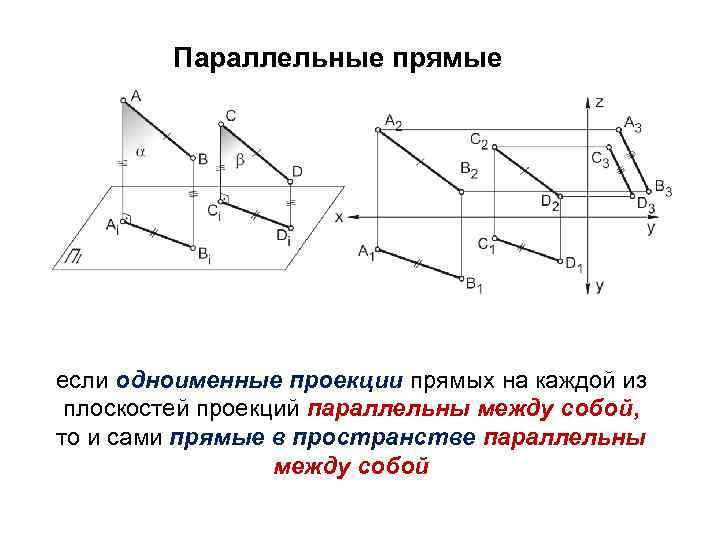
Параллельные прямые если одноименные проекции прямых на каждой из плоскостей проекций параллельны между собой, то и сами прямые в пространстве параллельны между собой

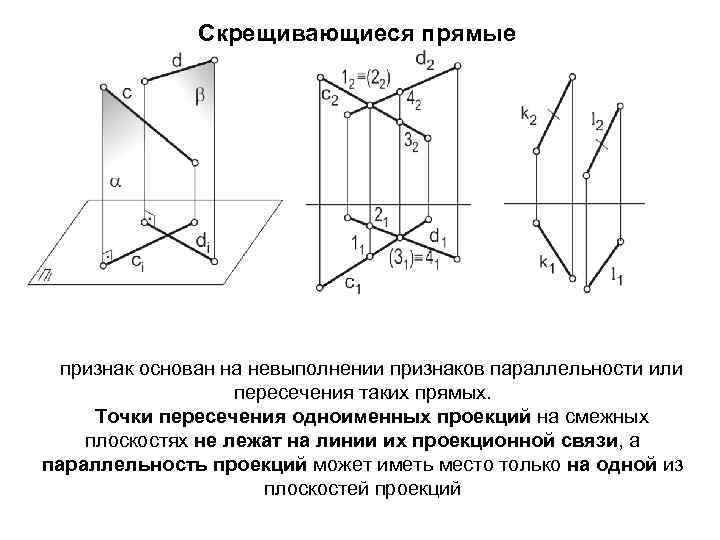
Скрещивающиеся прямые признак основан на невыполнении признаков параллельности или пересечения таких прямых. Точки пересечения одноименных проекций на смежных плоскостях не лежат на линии их проекционной связи, а параллельность проекций может иметь место только на одной из плоскостей проекций

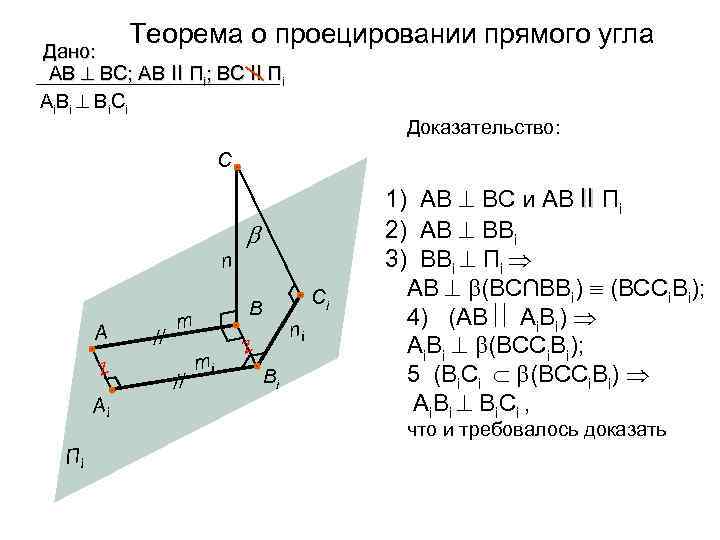
Теорема о проецировании прямого угла Дано: АВ ВС; АВ ll Пi; ВС ll Пi Аi. Вi Вi. Сi Доказательство: С n А Z Аi Пi // m // Сi В mi ni Z Вi 1) АВ ВС и АВ ll Пi 2) АВ ВВi 3) ВВi Пi АВ (ВС∩ВВi) (ВССi. Вi); 4) (АВ Аi. Вi) Аi. Вi (ВССi. Вi); 5 (Вi. Сi (ВССi. Вi) Аi. Вi Вi. Сi , что и требовалось доказать

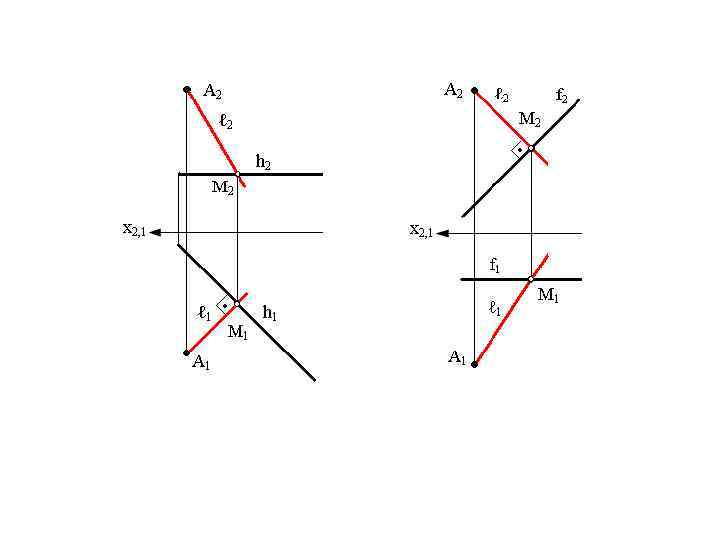
Преобразование комплексного чертежа

Способ замены плоскостей проекций

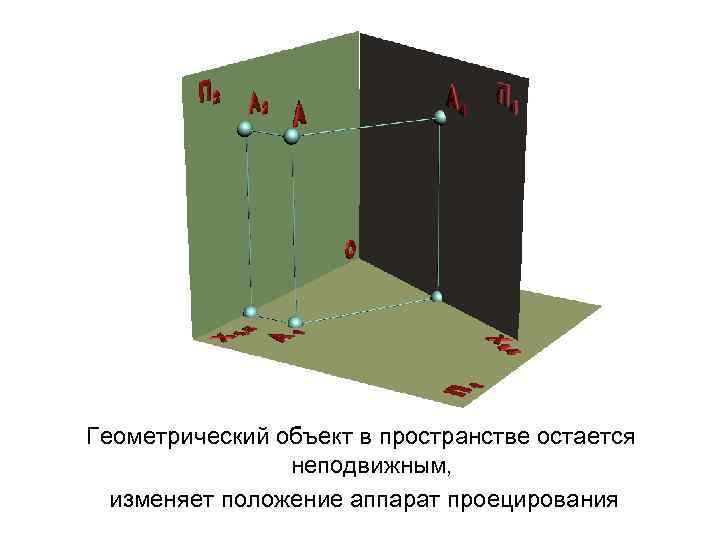
Геометрический объект в пространстве остается неподвижным, изменяет положение аппарат проецирования

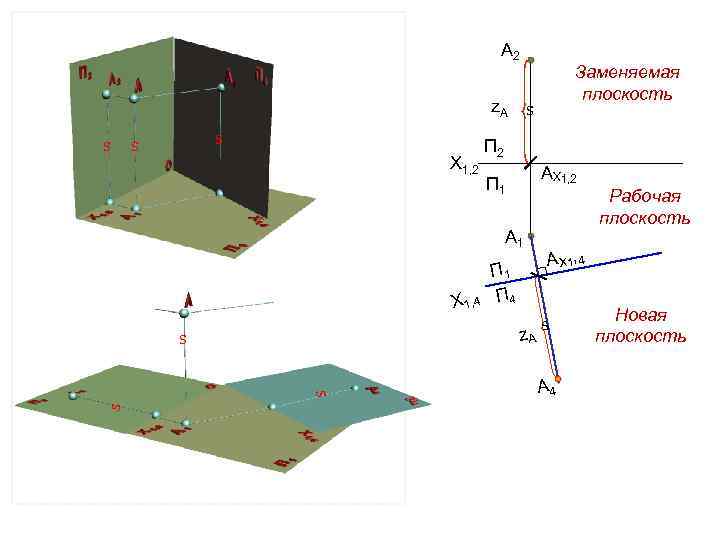
А 2 z. A s s s Х 1, 2 s П 2 АХ 1, 2 П 1 А 1 Х 1, 4 s s П 1 П 4 z. A s Заменяемая плоскость Рабочая плоскость АХ 1, 4 s А 4 Новая плоскость

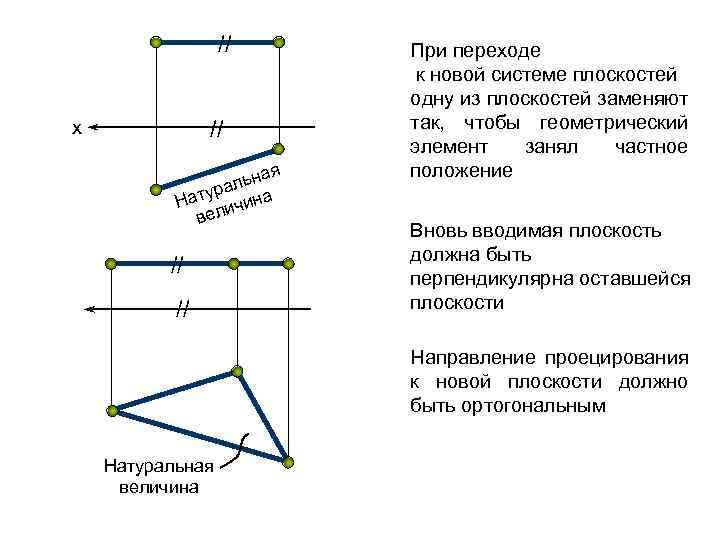
// // х я ьна л тура ина На ч ели в // // При переходе к новой системе плоскостей одну из плоскостей заменяют так, чтобы геометрический элемент занял частное положение Вновь вводимая плоскость должна быть перпендикулярна оставшейся плоскости Направление проецирования к новой плоскости должно быть ортогональным Натуральная величина

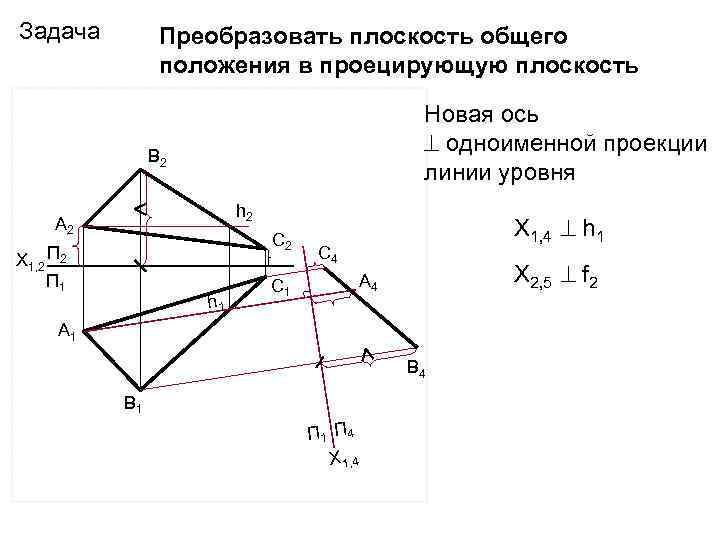
Задача Преобразовать плоскость общего положения в проецирующую плоскость Новая ось одноименной проекции линии уровня В 2 h 2 А 2 С 2 Х 1, 2 П 1 h 1 С 1 Х 1, 4 h 1 С 4 Х 2, 5 f 2 А 4 А 1 В 4 В 1 П 4 Х 1, 4

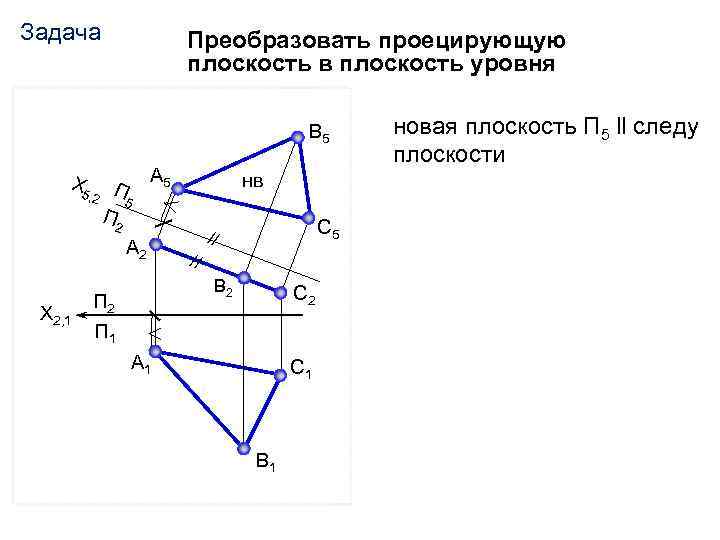
Задача Преобразовать проецирующую плоскость в плоскость уровня В 5 Х 5 , 2 П 5 П 2 А 5 А 2 Х 2, 1 нв С 5 // // В 2 П 1 С 2 А 1 С 1 В 1 новая плоскость П 5 ll следу плоскости

задачи, которые можно решить методом замены плоскостей проекций

1. Определение натуральной величины отрезка 2. Определение расстояния от точки до прямой (прямую преобразовать в проецирующую) 3. Определение расстояния между параллельными прямыми (прямые преобразовать в проецирующие) 4. Определение величины двугранного угла (общее ребро преобразовать в проецирующую прямую) 5. Определение расстояния между скрещивающими прямыми (одну из прямых преобразовать в проецирующую)

6. Определение расстояния от точки до плоскости (плоскость преобразовать в след) 7. Определение расстояния между параллельными плоскостями (обе плоскости преобразовать в след) 8. Определение натуральной величины плоской фигуры 9. Определение угла наклона прямой к плоскости 10. Определение угла наклона плоскости к плоскостям проекций

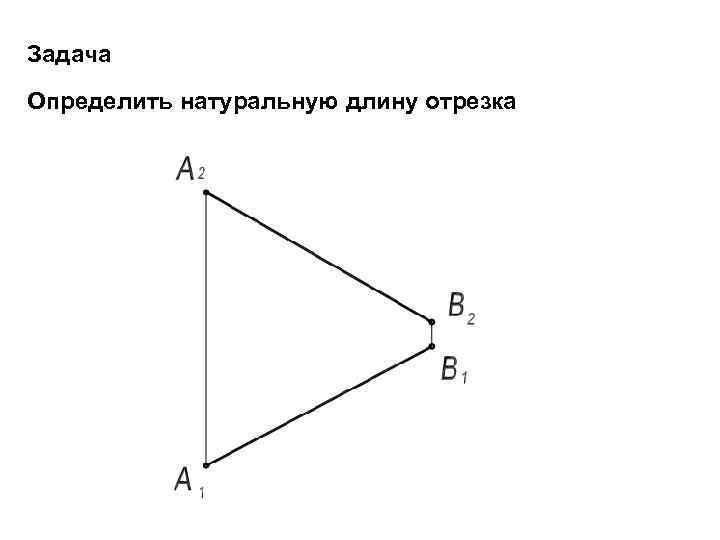
Задача Определить натуральную длину отрезка