Прямая доцент кафедры Инженерная графика и дизайн НИТУ

Прямая доцент кафедры Инженерная графика и дизайн НИТУ «МИСи. С» Дербенева О. Л. olderbeneva@mail. ru 2015 г. 1

Содержание лекции • • Задание прямой. Прямая общего положения. Прямые частного положения. Принадлежность точки прямой. Деление отрезка прямой линии в заданном отношении. Определение длины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций. Следы прямой линии. Взаимное положение прямых. Проекции плоских углов. 2

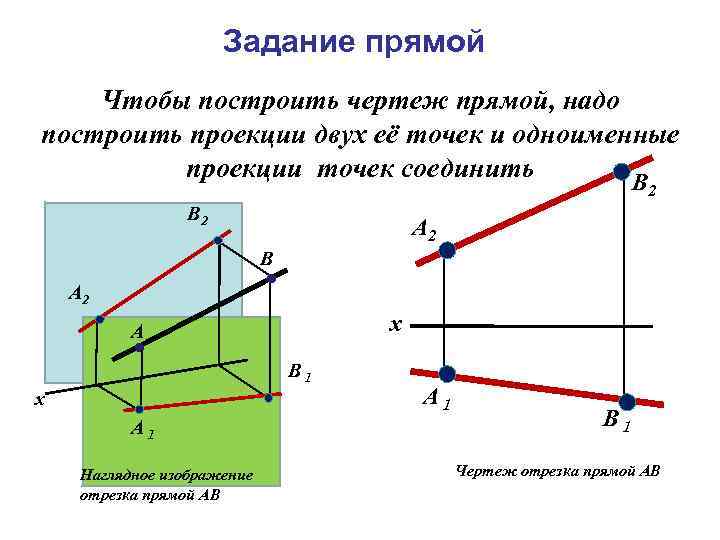Задание прямой Чтобы построить чертеж прямой, надо построить проекции двух её точек и одноименные проекции точек соединить В 2 А 2 В А 2 х А В 1 х А 1 Наглядное изображение отрезка прямой АВ А 1 В 1 Чертеж отрезка прямой АВ

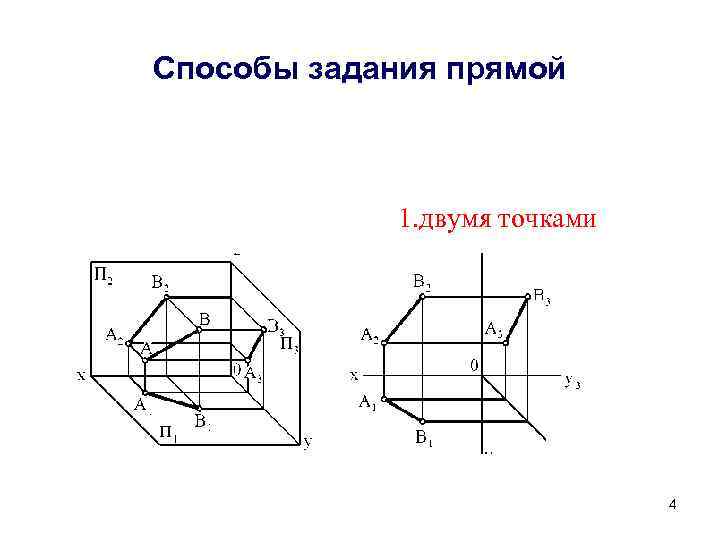Способы задания прямой 1. двумя точками 4

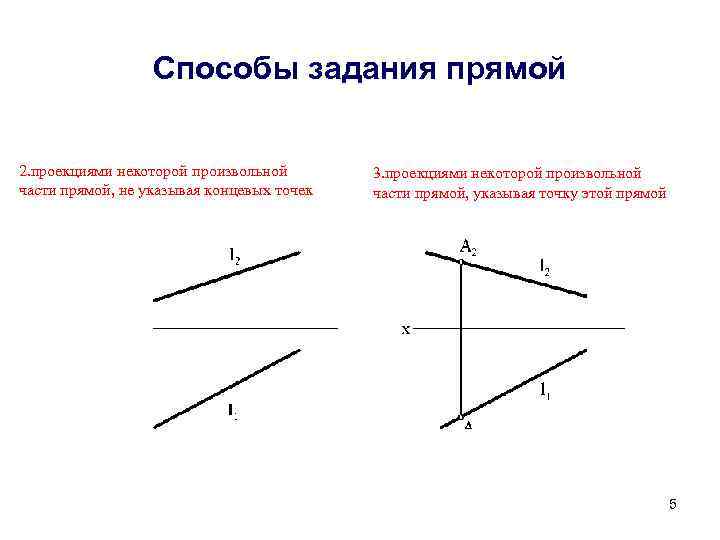Способы задания прямой 2. проекциями некоторой произвольной части прямой, не указывая концевых точек 3. проекциями некоторой произвольной части прямой, указывая точку этой прямой 5

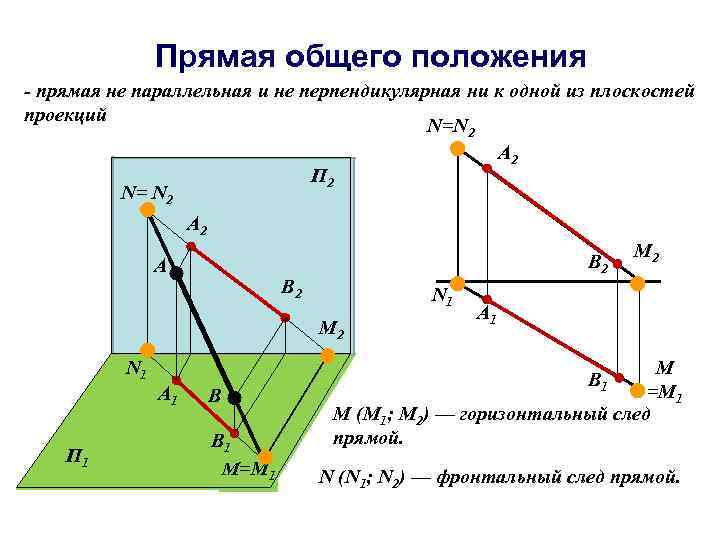Прямая общего положения - прямая не параллельная и не перпендикулярная ни к одной из плоскостей проекций N=N 2 A 2 П 2 N= N 2 A B 2 N 1 M 2 N 1 A 1 П 1 B B 1 M=M 1 M 2 A 1 M =M 1 M (M 1; M 2) — горизонтальный след прямой. B 1 N (N 1; N 2) — фронтальный след прямой.

Прямые частного положения Прямая уровня Проецирующая прямая (прямая, параллельная какой-нибудь одной плоскости проекций): (прямая, перпендикулярная к какой-нибудь одной плоскости проекций) : v. Горизонтальнопроецирующая; v. Фронталь v. Профильная v. Фронтальнопроецирующая; v. Профильнопроецирующая.

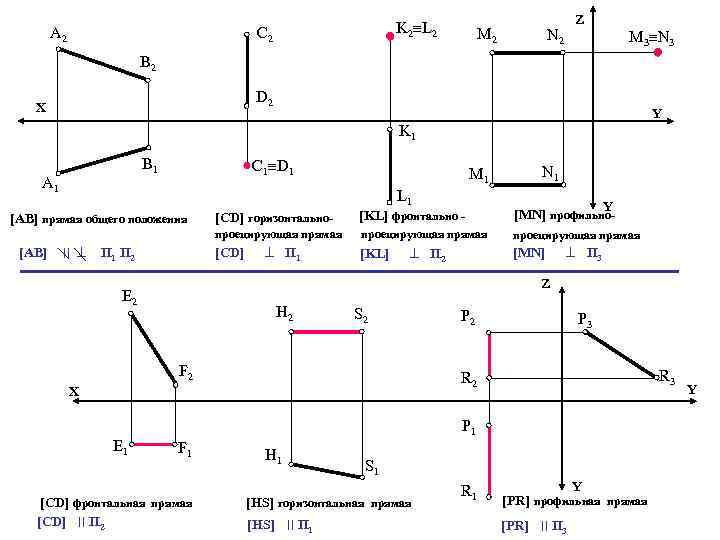A 2 K 2 L 2 С 2 M 2 Z N 2 M 3 N 3 В 2 D 2 Х Y K 1 В 1 A 1 C 1 D 1 M 1 L 1 N 1 [АВ] ׀׀ [CD] горизонтально- [KL] фронтально - Y [MN] профильно- проецирующая прямая [АВ] прямая общего положения проецирующая прямая [СD] П 1 П 2 П 1 [KL] П 2 П 3 Z E 2 H 2 S 2 F 2 P 3 R 2 Х E 1 [MN] P 1 F 1 [CD] фронтальная прямая [CD] ׀׀ П 2 H 1 S 1 [HS] горизонтальная прямая [HS] ׀׀ П 1 R 1 Y [PR] профильная прямая [PR] ׀׀ П 3 Y

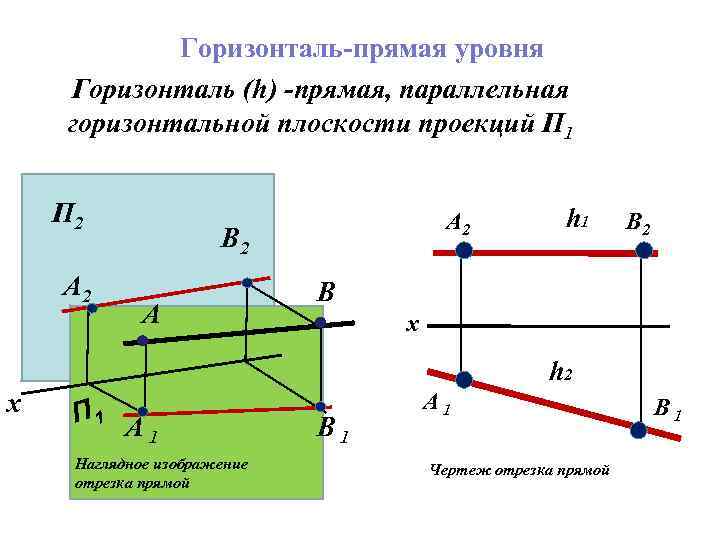Горизонталь-прямая уровня Горизонталь (h) -прямая, параллельная горизонтальной плоскости проекций П 1 П 2 A 2 B 2 А h 1 B 2 В х h 2 х П 1 A 1 Наглядное изображение отрезка прямой B 1 A 1 Чертеж отрезка прямой B 1

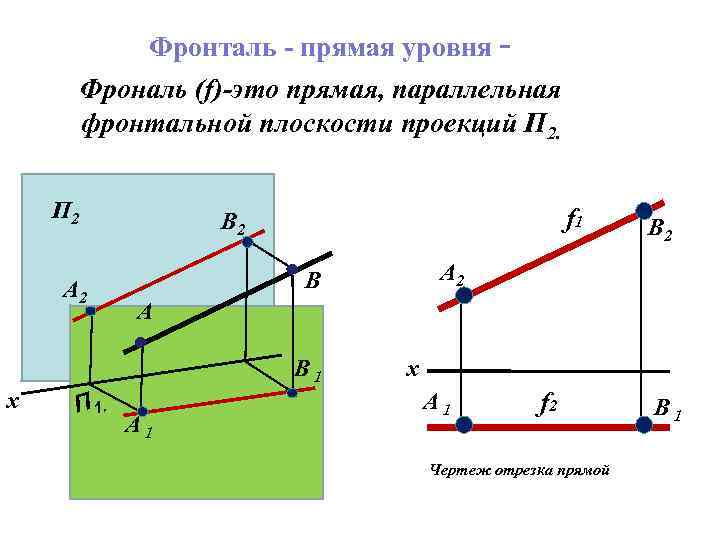Фронталь - прямая уровня Фрональ (f)-это прямая, параллельная фронтальной плоскости проекций П 2 A 2 f 1 B 2 П 1. A 2 В А B 1 х B 2 A 1 Наглядное изображение отрезка прямой х A 1 f 2 Чертеж отрезка прямой B 1

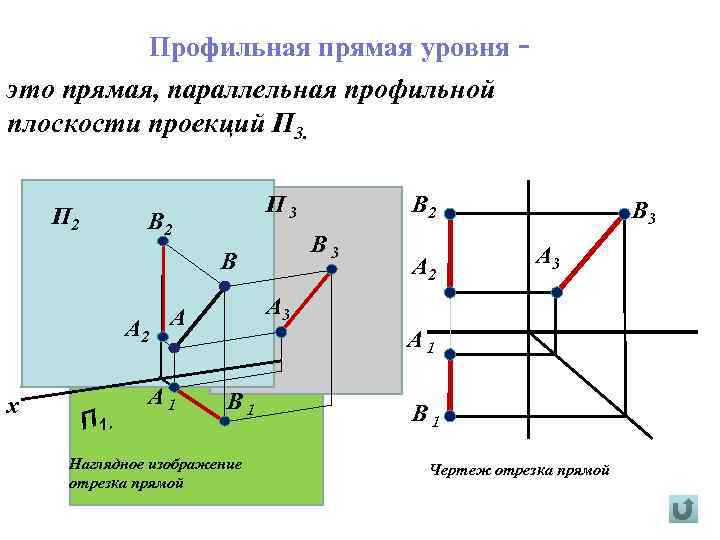Профильная прямая уровня это прямая, параллельная профильной плоскости проекций П 3. П 2 П 3 B 2 B 3 В A 2 х П 1. A 2 B 3 A 3 А A 1 B 2 A 1 B 1 Наглядное изображение отрезка прямой B 1 Чертеж отрезка прямой

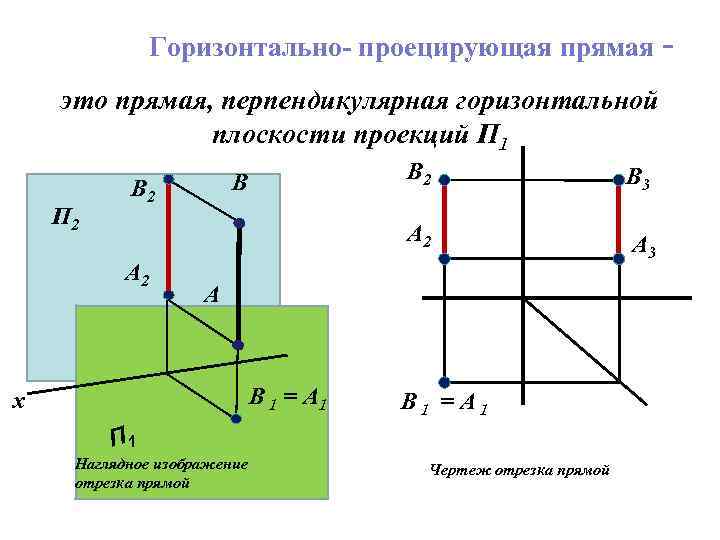Горизонтально- проецирующая прямая это прямая, перпендикулярная горизонтальной плоскости проекций П 1 П 2 B 3 A 2 B 2 В A 3 А B 1 = A 1 х B 1 = A 1 П 1 Наглядное изображение отрезка прямой Чертеж отрезка прямой

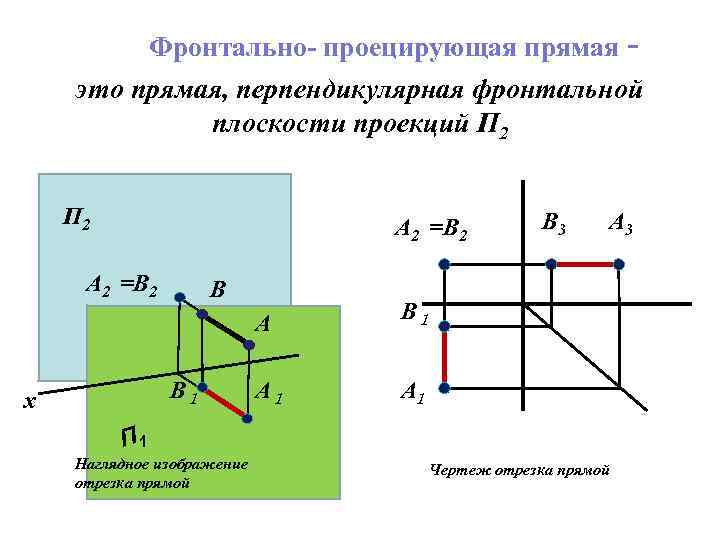Фронтально- проецирующая прямая это прямая, перпендикулярная фронтальной плоскости проекций П 2 A 2 =B 2 В А B 1 х A 3 B 1 A 1 B 3 A 1 П 1 Наглядное изображение отрезка прямой Чертеж отрезка прямой

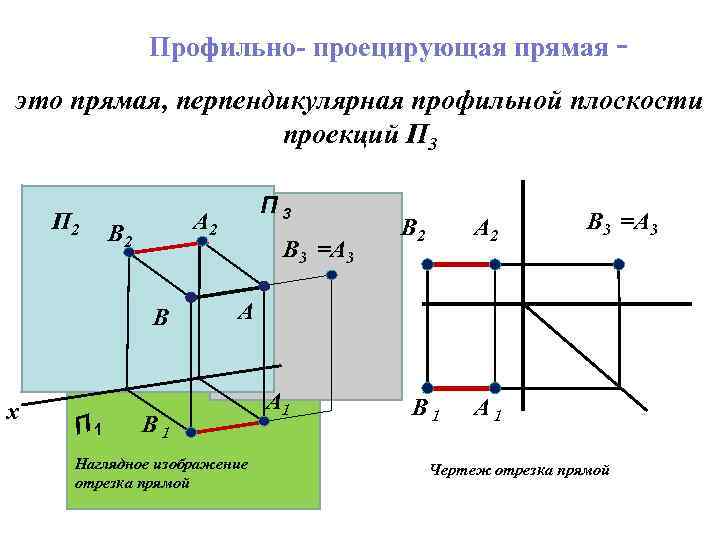Профильно- проецирующая прямая это прямая, перпендикулярная профильной плоскости проекций П 3 П 2 A 2 B 2 В х П 1 П 3 B 3 =A 3 B 2 A 2 B 3 =A 3 А B 1 Наглядное изображение отрезка прямой A 1 B 1 A 1 Чертеж отрезка прямой

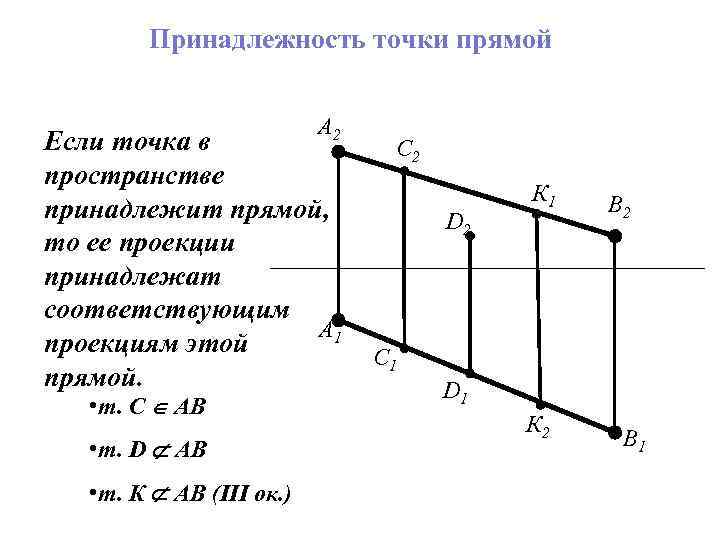Принадлежность точки прямой А 2 Если точка в пространстве принадлежит прямой, то ее проекции принадлежат соответствующим А 1 проекциям этой прямой. • т. С АВ • т. D АВ • т. К АВ (III ок. ) С 2 D 2 К 1 В 2 С 1 D 1 К 2 В 1

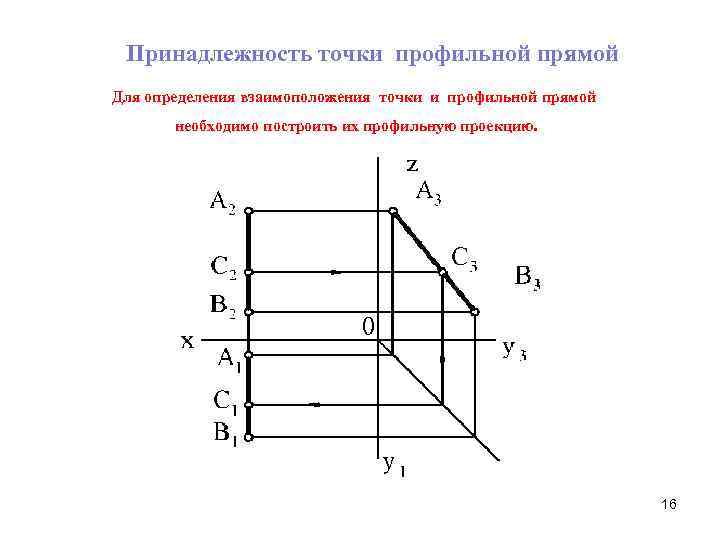Принадлежность точки профильной прямой Для определения взаимоположения точки и профильной прямой необходимо построить их профильную проекцию. 16

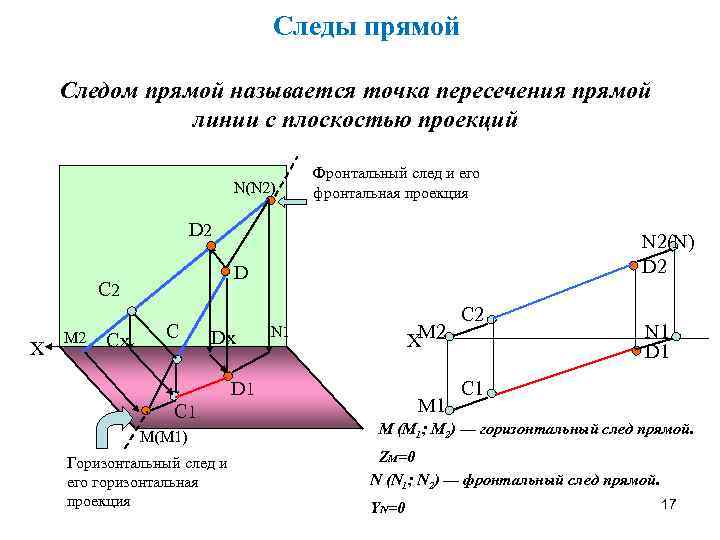Следы прямой Следом прямой называется точка пересечения прямой линии с плоскостью проекций N(N 2) Фронтальный след и его фронтальная проекция D 2 D С 2 Х M 2 Сх N 2(N) D 2 С Dx ХM 2 N 1 D 1 C 1 М(M 1) Горизонтальный след и его горизонтальная проекция M 1 С 2 N 1 D 1 С 1 M (M 1; M 2) — горизонтальный след прямой. ZM=0 N (N 1; N 2) — фронтальный след прямой. YN=0 17

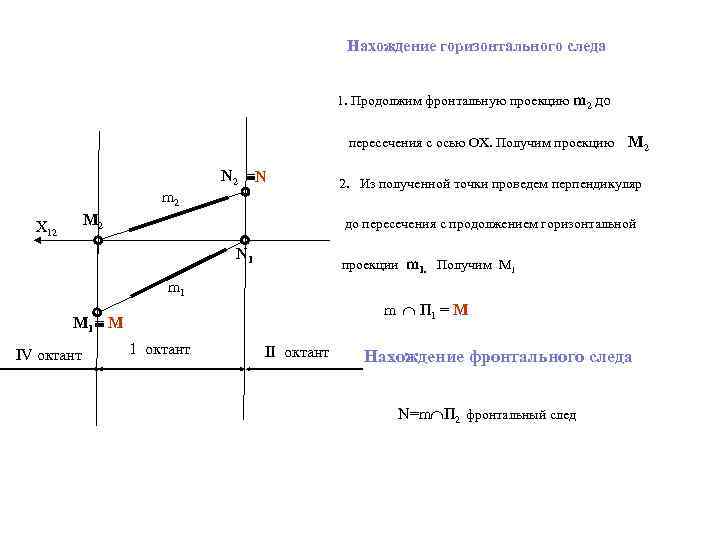Нахождение горизонтального следа 1. Продолжим фронтальную проекцию m 2 до пересечения с осью ОХ. Получим проекцию N 2 N m 2 M 2 Х 12 2. Из полученной точки проведем перпендикуляр до пересечения с продолжением горизонтальной N 1 проекции m 1. Получим М 1 m П 1 = М M 1 M IV октант М 2 1 октант II октант Нахождение фронтального следа N=m П 2 фронтальный след

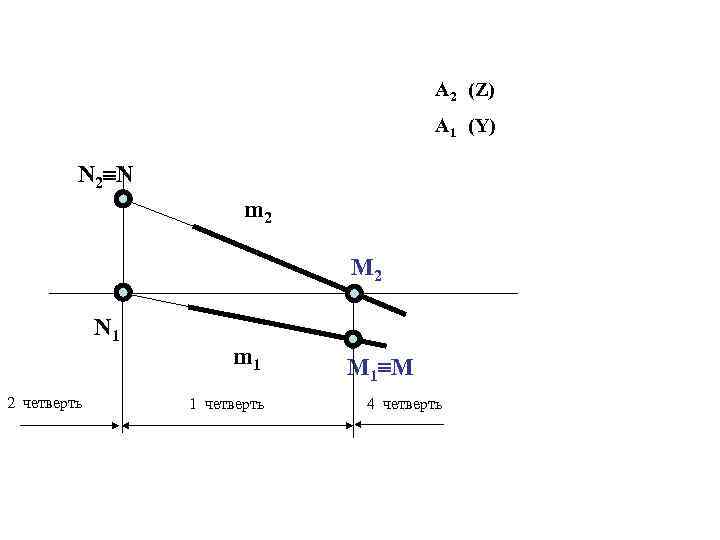А 2 (Z) А 1 (Y) N 2 N m 2 M 2 N 1 2 четверть m 1 1 четверть M 1 M 4 четверть

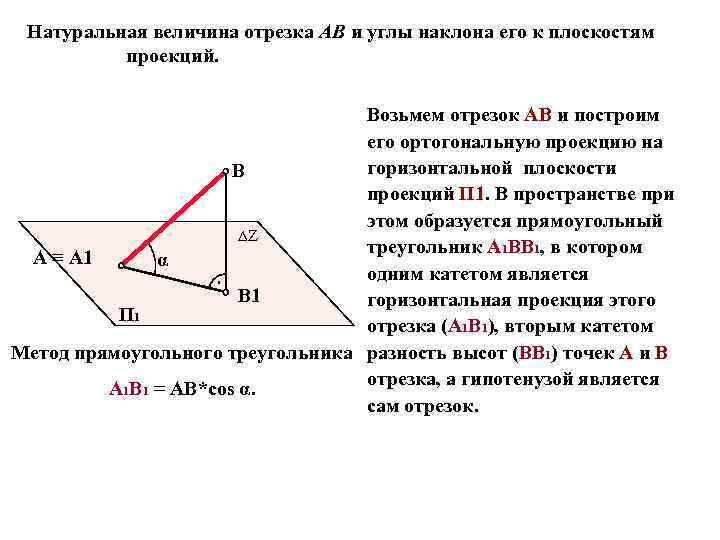Натуральная величина отрезка АВ и углы наклона его к плоскостям проекций. Возьмем отрезок АВ и построим его ортогональную проекцию на горизонтальной плоскости B проекций П 1. В пространстве при этом образуется прямоугольный ∆Z треугольник А 1 BВ 1, в котором A ≡ А 1 α одним катетом является В 1 горизонтальная проекция этого П 1 отрезка (А 1 В 1), вторым катетом Метод прямоугольного треугольника разность высот (BВ 1) точек А и В отрезка, а гипотенузой является А 1 В 1 = АВ*соs α. сам отрезок.

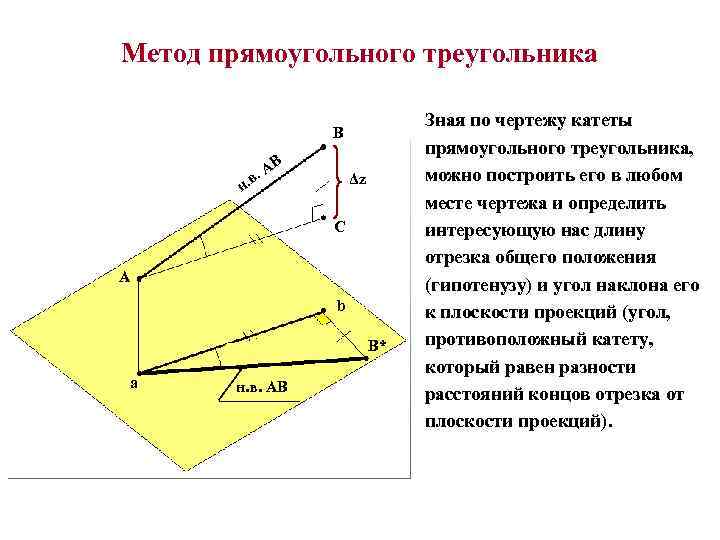Метод прямоугольного треугольника B В А. в. Δz н C A b B* a н. в. АВ Зная по чертежу катеты прямоугольного треугольника, можно построить его в любом месте чертежа и определить интересующую нас длину отрезка общего положения (гипотенузу) и угол наклона его к плоскости проекций (угол, противоположный катету, который равен разности расстояний концов отрезка от плоскости проекций).

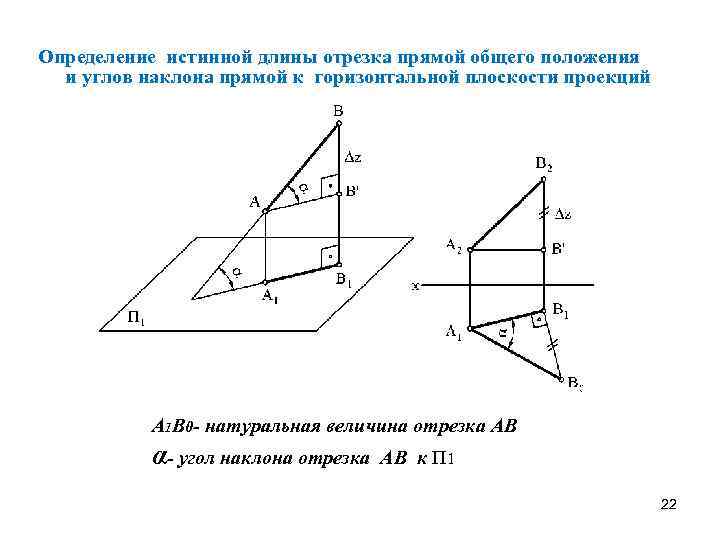Определение истинной длины отрезка прямой общего положения и углов наклона прямой к горизонтальной плоскости проекций А 1 В 0 - натуральная величина отрезка АВ α- угол наклона отрезка АВ к П 1 22

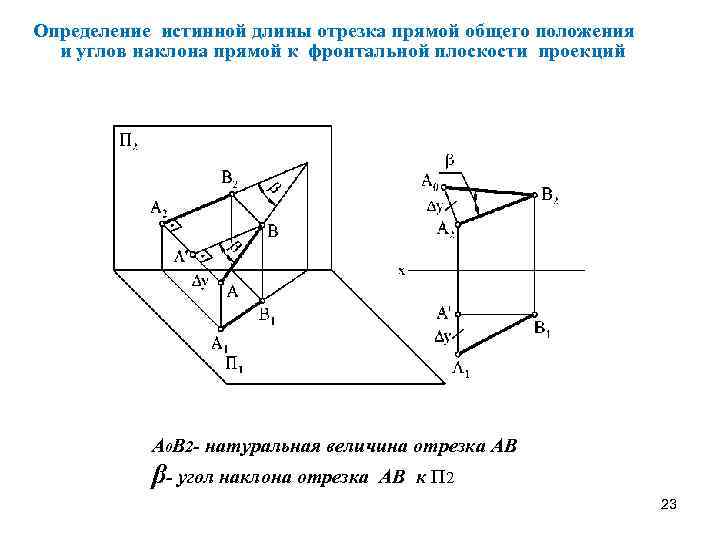Определение истинной длины отрезка прямой общего положения и углов наклона прямой к фронтальной плоскости проекций А 0 В 2 - натуральная величина отрезка АВ β- угол наклона отрезка АВ к П 2 23

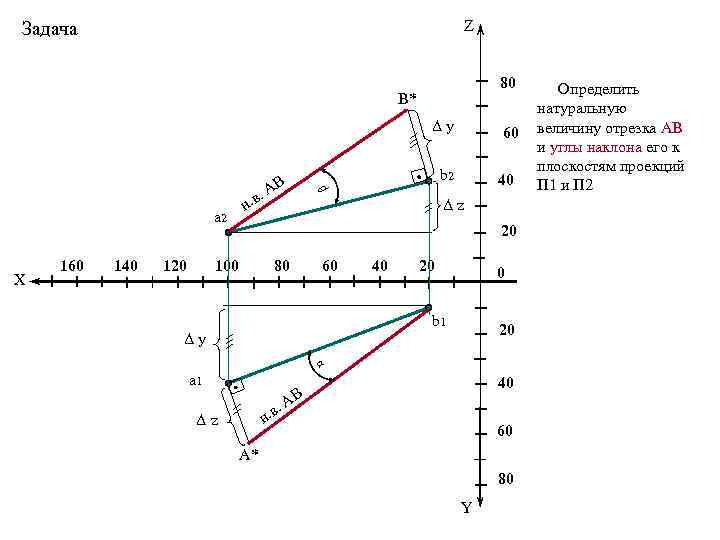Z Задача 80 B* . в. н a 2 X 160 140 120 АВ 60 b 2 40 β Δy Δz 20 100 80 60 40 20 0 b 1 20 Δy α a 1. н. в Δz 40 АВ 60 A* 80 Y Определить натуральную величину отрезка АВ и углы наклона его к плоскостям проекций П 1 и П 2

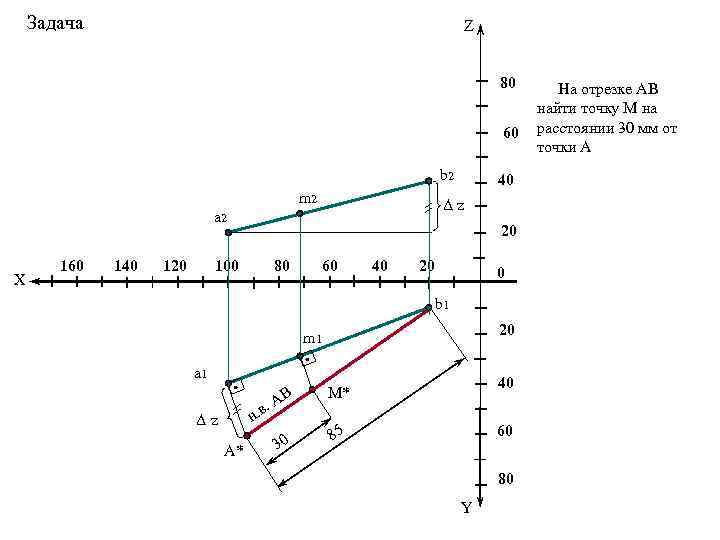Задача Z 80 60 b 2 m 2 Δz a 2 X 160 140 120 40 20 100 80 60 40 20 0 b 1 20 m 1 a 1 В. А н. в Δz A* 30 40 M* 60 85 80 Y На отрезке АВ найти точку М на расстоянии 30 мм от точки А

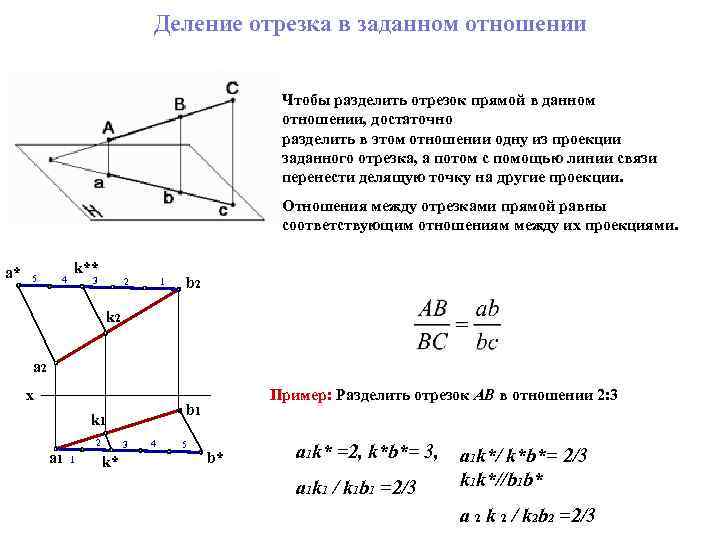Деление отрезка в заданном отношении Чтобы разделить отрезок прямой в данном отношении, достаточно разделить в этом отношении одну из проекции заданного отрезка, а потом с помощью линии связи перенести делящую точку на другие проекции. Отношения между отрезками прямой равны соответствующим отношениям между их проекциями. a* 5 4 k** 3 2 1 b 2 k 2 а 2 x k 1 2 a 1 1 3 k* Пример: Разделить отрезок АВ в отношении 2: 3 b 1 4 5 b* a 1 k* =2, k*b*= 3, a 1 k 1 / k 1 b 1 =2/3 a 1 k*/ k*b*= 2/3 k 1 k*//b 1 b* a 2 k 2 / k 2 b 2 =2/3

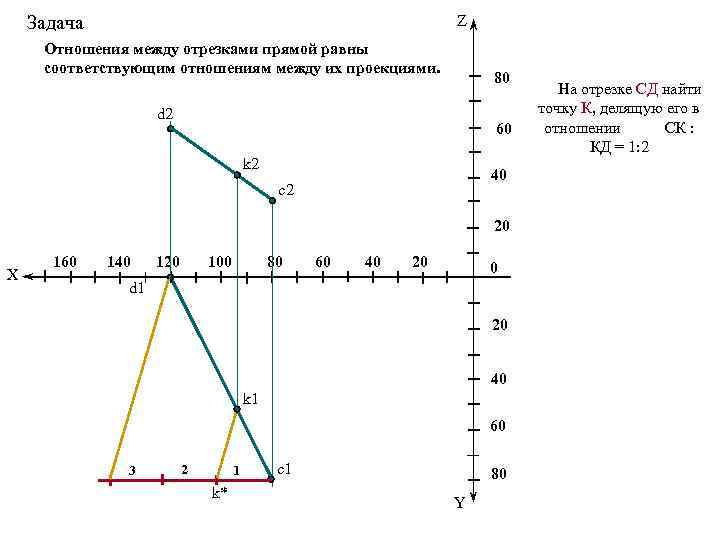Задача Z Отношения между отрезками прямой равны соответствующим отношениям между их проекциями. 80 d 2 60 k 2 40 c 2 20 X 160 140 120 100 80 60 40 20 0 d 1 20 40 k 1 60 3 2 1 k* c 1 80 Y На отрезке СД найти точку К, делящую его в отношении СК : КД = 1: 2

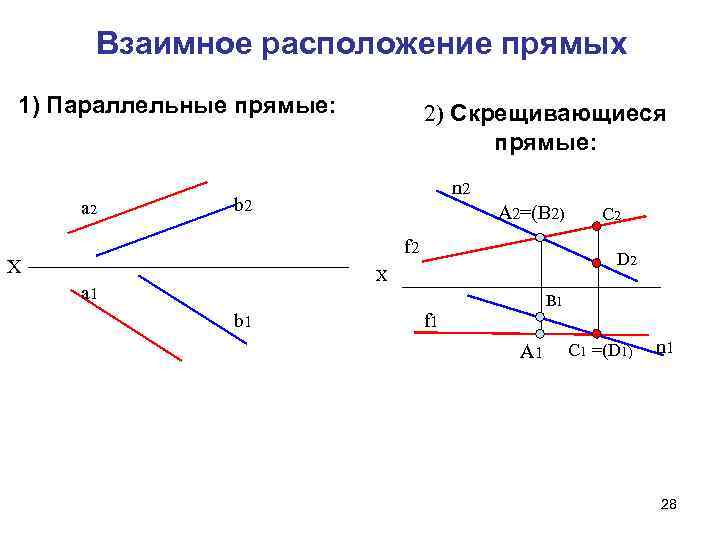Взаимное расположение прямых 1) Параллельные прямые: а 2 2) Скрещивающиеся прямые: n 2 b 2 A 2=(B 2) f 2 Х D 2 Х a 1 b 1 C 2 B 1 f 1 A 1 C 1 =(D 1) n 1 28

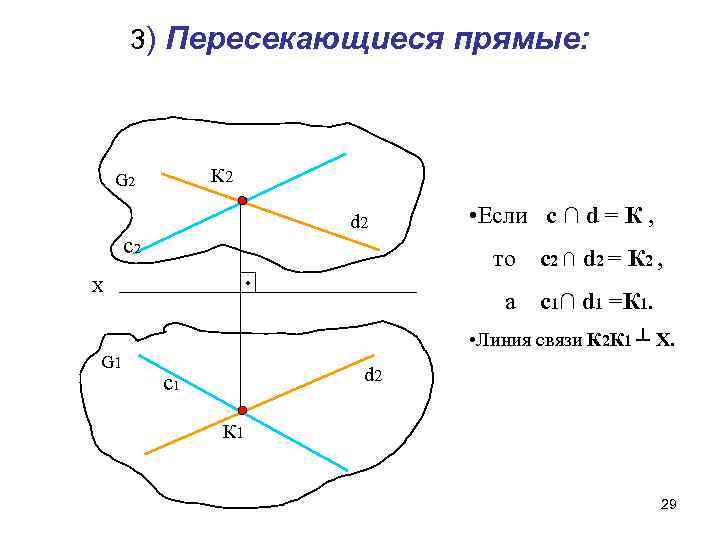3) Пересекающиеся прямые: К 2 G 2 d 2 с2 • Если с ∩ d = К , то а Х с 2 ∩ d 2 = К 2 , с1∩ d 1 =К 1. • Линия связи К 2 К 1 ┴ Х. G 1 d 2 с1 К 1 29

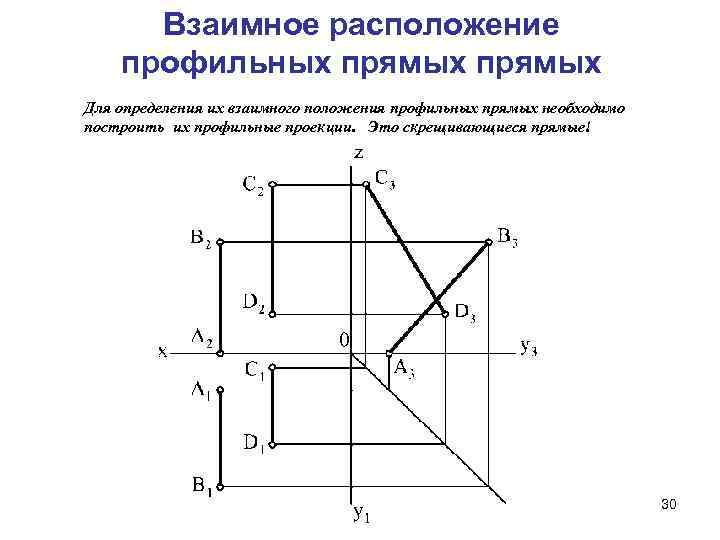Взаимное расположение профильных прямых Для определения их взаимного положения профильных прямых необходимо построить их профильные проекции. Это скрещивающиеся прямые! 30

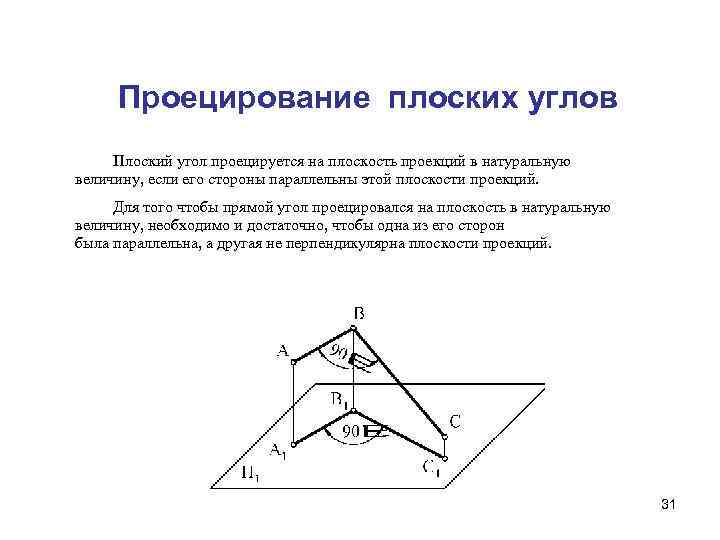Проецирование плоских углов Плоский угол проецируется на плоскость проекций в натуральную величину, если его стороны параллельны этой плоскости проекций. Для того чтобы прямой угол проецировался на плоскость в натуральную величину, необходимо и достаточно, чтобы одна из его сторон была параллельна, а другая не перпендикулярна плоскости проекций. 31

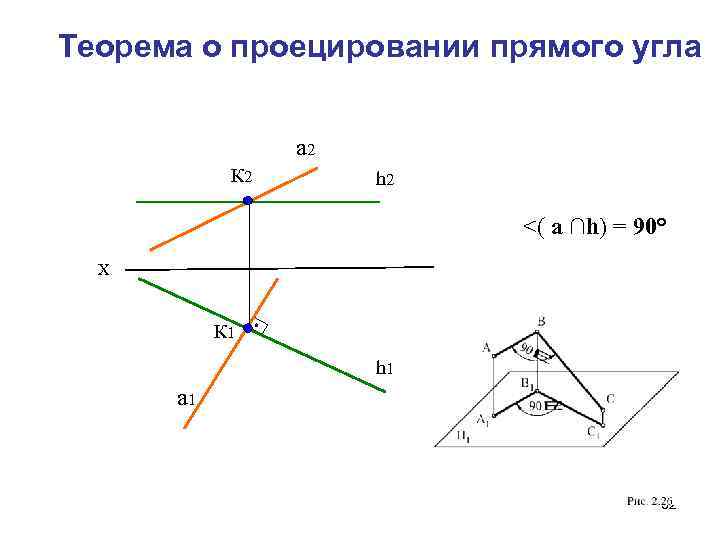Теорема о проецировании прямого угла а 2 К 2 h 2 <( a ∩h) = 90° Х К 1 h 1 а 1 32

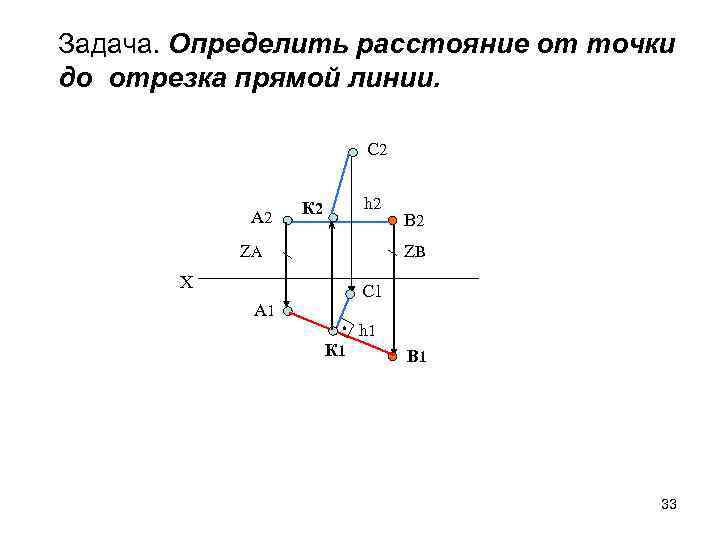Задача. Определить расстояние от точки до отрезка прямой линии. С 2 А 2 h 2 К 2 ZА В 2 ZВ Х С 1 А 1 К 1 h 1 В 1 33

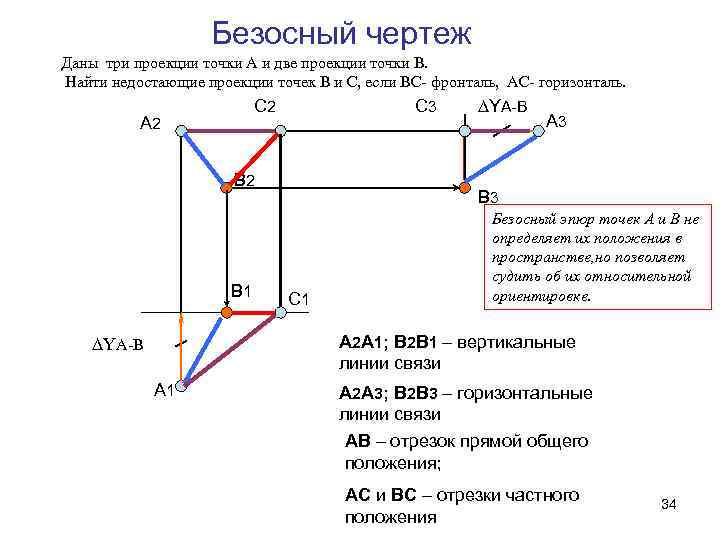Безосный чертеж Даны три проекции точки А и две проекции точки В. Найти недостающие проекции точек В и С, если ВС- фронталь, АС- горизонталь. С 2 А 2 С 3 B 2 B 1 ∆YA-B А 3 B 3 С 1 Безосный эпюр точек А и В не определяет их положения в пространстве, но позволяет судить об их относительной ориентировке. А 2 А 1; В 2 В 1 – вертикальные линии связи ∆YA-B А 1 А 2 А 3; В 2 В 3 – горизонтальные линии связи АВ – отрезок прямой общего положения; АС и ВС – отрезки частного положения 34

Рекомендуемая литература Основная литература 1. Соломонов К. Н. , Чиченёва О. Н. , Бусыгина Е. Б. Основы начертательной геометрии. -М. : МИСи. С, 2003 2. Соломонов К. Н. , Чиченёва О. Н. , Бусыгина Е. Б. Основы технического черчения. – М. : МИСи. С, 2004 3. Чекмарев А. А. Инженерная графика. М. : Высшая школа, 1998 4. Сборник «Национальные стандарты» . ЕСКД. ГОСТ 2. 301 -68 2. 321 -84. -М. : ИПК Издательство Стандартов, 2004 5. Крылов Н. Н. , Иконникова Г. С. , Николаев В. Л. , Васильев В. Е. , Начертательная геометрия. -М. : Высш. шк. , 2002. -224 с. Средства обеспечения освоения дисциплины 1. Пакет Auto. CAD, Компас 3 D, Симплекс 2. Курс лекций, созданный с использованием графического «Power Point « и средств Internet. редактора 35