Прямая 1 Задание прямой 2 Прямые общего положения

Прямая 1. Задание прямой 2. Прямые общего положения 3. Прямые частного положения 4. Принадлежность точки прямой. Деление отрезка прямой линии в данном отношении 5. Определение длины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций 6. Следы прямой линии

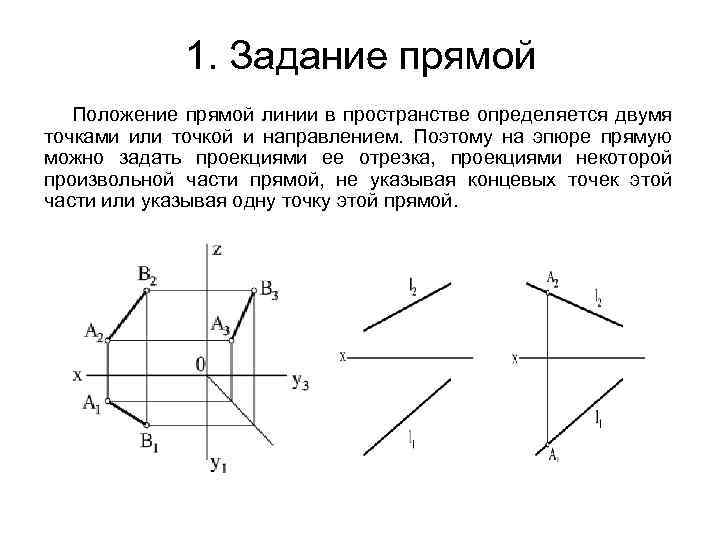
1. Задание прямой Положение прямой линии в пространстве определяется двумя точками или точкой и направлением. Поэтому на эпюре прямую можно задать проекциями ее отрезка, проекциями некоторой произвольной части прямой, не указывая концевых точек этой части или указывая одну точку этой прямой.

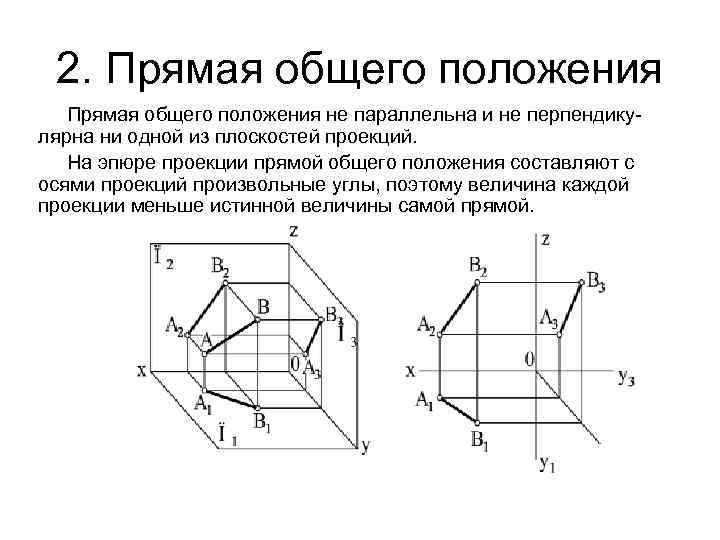
2. Прямая общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций. На эпюре проекции прямой общего положения составляют с осями проекций произвольные углы, поэтому величина каждой проекции меньше истинной величины самой прямой.

3. Прямая частного положения Прямые, параллельные или перпендикулярные плоскостям проекций называют прямыми частного положения. Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня: 1) прямую, параллельную горизонтальной плоскости проекций; называют горизонтальной или горизонталью h;

н. в.

2) прямую, параллельную фронтальной плоскости проекций; называют фронтальной или фронталью f; н. в.

3) прямую, параллельную профильной плоскости проекций, называют профильной р. н. в.

Каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона ( , , ), которые эта прямая образует с двумя другими плоскостями проекций, проецируются на эту плоскость без искажения. Все точки горизонтальной прямой АВ удалены на одинаковые расстояния от плоскости П 1, поэтому фронтальная проекция любой горизонтали параллельна оси ОХ, а профильная проекция – параллельна оси ОУ. Величина фронтальной и профильной проекций будут меньше натуральной величины самой прямой.

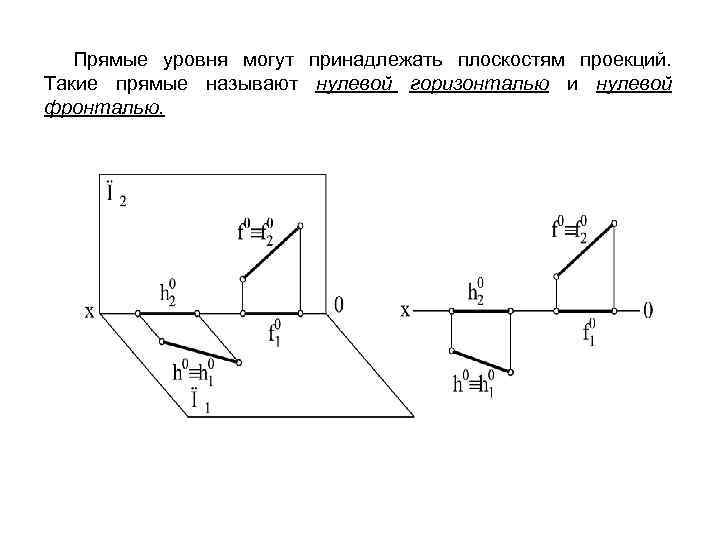
Прямые уровня могут принадлежать плоскостям проекций. Такие прямые называют нулевой горизонталью и нулевой фронталью.

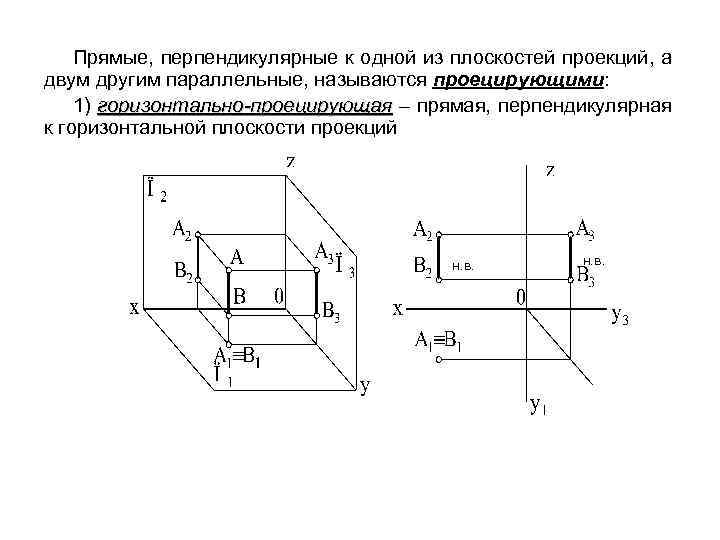
Прямые, перпендикулярные к одной из плоскостей проекций, а двум другим параллельные, называются проецирующими: 1) горизонтально-проецирующая – прямая, перпендикулярная к горизонтальной плоскости проекций н. в.

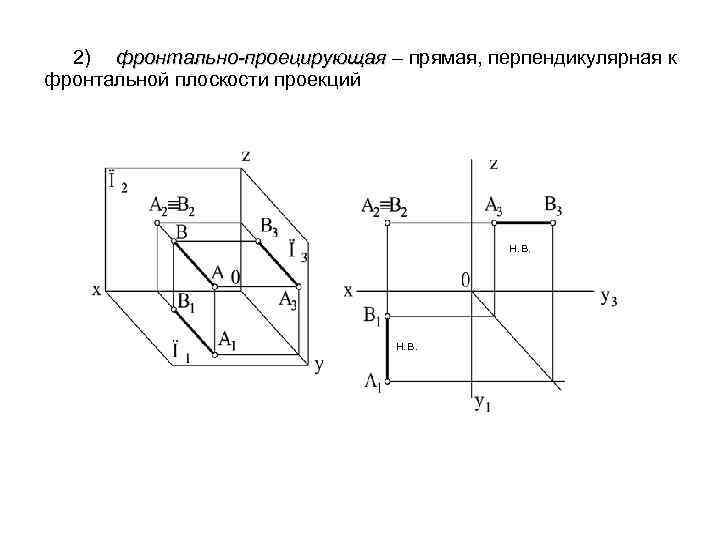
2) фронтально-проецирующая – прямая, перпендикулярная к фронтальной плоскости проекций н. в.

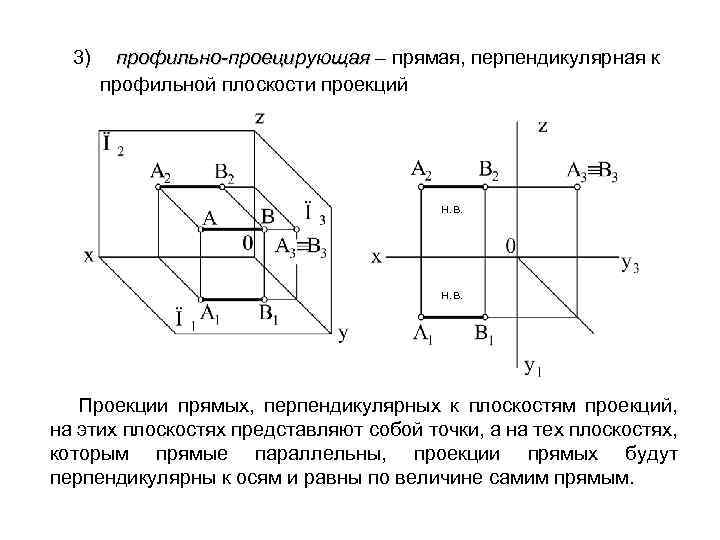
3) профильно-проецирующая – прямая, перпендикулярная к профильной плоскости проекций н. в. Проекции прямых, перпендикулярных к плоскостям проекций, на этих плоскостях представляют собой точки, а на тех плоскостях, которым прямые параллельны, проекции прямых будут перпендикулярны к осям и равны по величине самим прямым.

4. Принадлежность точки прямой. Деление отрезка прямой линии в данном отношении Если точка лежит на прямой, то ее проекции будут лежать на одноименных проекциях этой прямой. Точка А принадлежит прямой l, т. к. А 2 l 2, А 1 l 1, точки С и В – не принадлежат, т. к. С 1 l 1, а В 2 l 2.

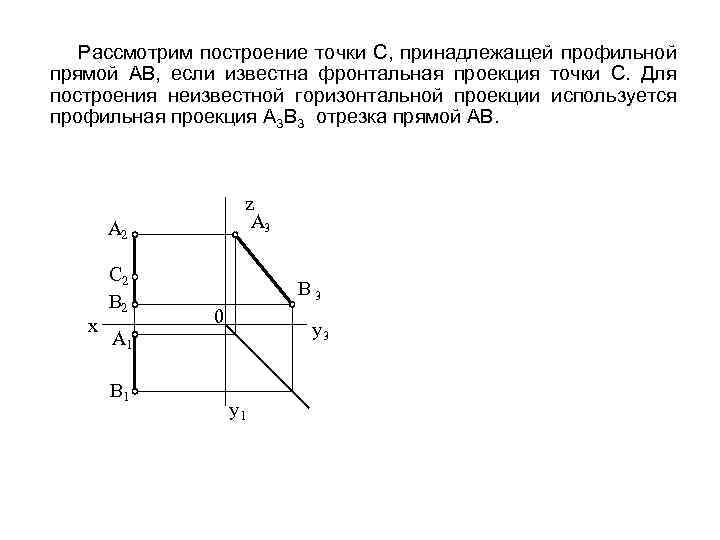
Рассмотрим построение точки С, принадлежащей профильной прямой АВ, если известна фронтальная проекция точки С. Для построения неизвестной горизонтальной проекции используется профильная проекция А 3 В 3 отрезка прямой АВ. z A 3 A 2 C 2 B 2 x A 1 B 3 0 y 3 y 1

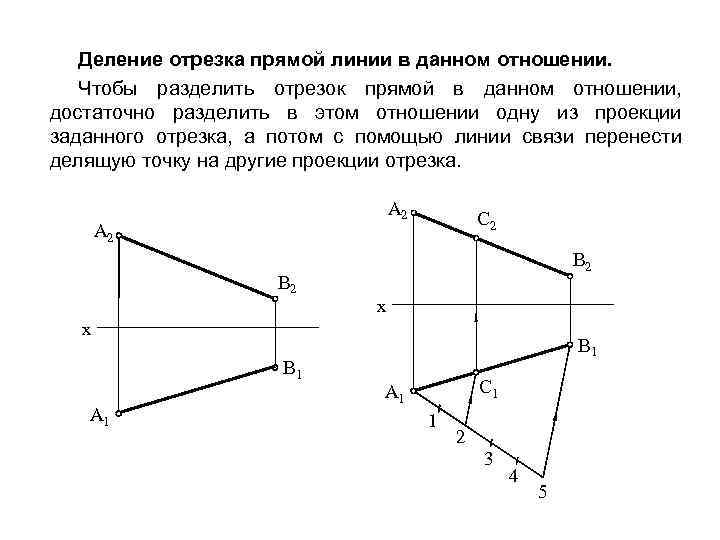
Деление отрезка прямой линии в данном отношении. Чтобы разделить отрезок прямой в данном отношении, достаточно разделить в этом отношении одну из проекции заданного отрезка, а потом с помощью линии связи перенести делящую точку на другие проекции отрезка. A 2 B 2 C 2 B 2 x x B 1 A 1 B 1 C 1 A 1 1 2 3 4 5

5. Определение длины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций Рассмотрим проецирование отрезка АВ на горизонтальную плоскость П 1. Через точку А проведена прямая АВ, параллельная горизонтальной проекции отрезка А 1 В 1. В полученном прямоугольном треугольнике АВВ' катеты АВ' равен проекции А 1 В 1, а ВВ' равен разности расстояний концов отрезка от плоскости проекций П 1( z). Гипотенуза этого треугольника равна длине отрезка АВ. Угол в треугольнике АВВ' является углом наклона отрезка прямой АВ к плоскости П 1.

Для определения угла наклона отрезка прямой АВ на фронтальной плоскости проекций П 2 строят прямоугольный треугольник аналогичным путем: через точку В проводят прямую ВА', параллельную А 2 В 2. Катет ВА'=А 2 В 2, а второй катет АА' равен ∆у – разности расстояний точек А и В от плоскости П 2.

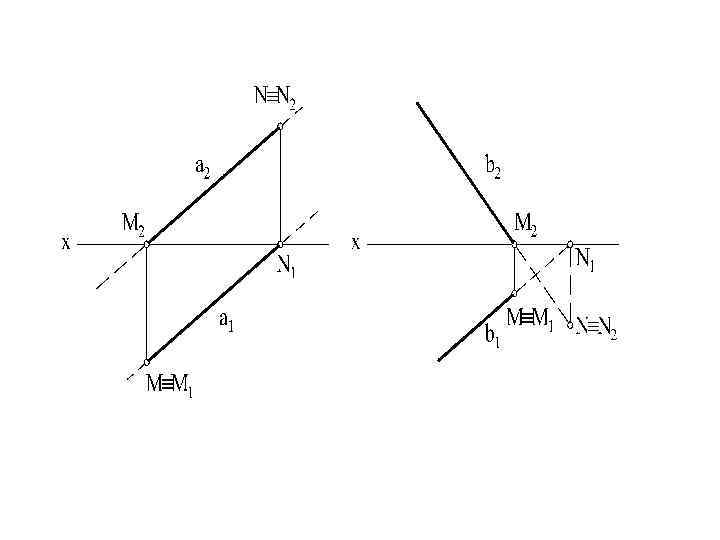
6. Следы прямой линии Прямая общего положения пересекает все плоскости проекций. Точки пересечения прямой линии с плоскостями проекций называют следами прямой. Точка М – горизонтальный след прямой, точка N – фронтальный. Горизонтальная проекция М 1 горизонтального следа прямой совпадает с самим следом – точкой М, а фронтальная проекция этого следа М 2 лежит на оси ОХ. Фронтальная проекция N 2 фронтального следа прямой совпадает с точкой N, а горизонтальная проекция N 1 лежит на оси ОХ. Для построения горизонтального следа М прямой необходимо продолжить фронтальную проекцию прямой до пересечения с осью ОХ и в этой точке восставить перпендикуляр до пересечения с горизонтальной проекцией прямой.

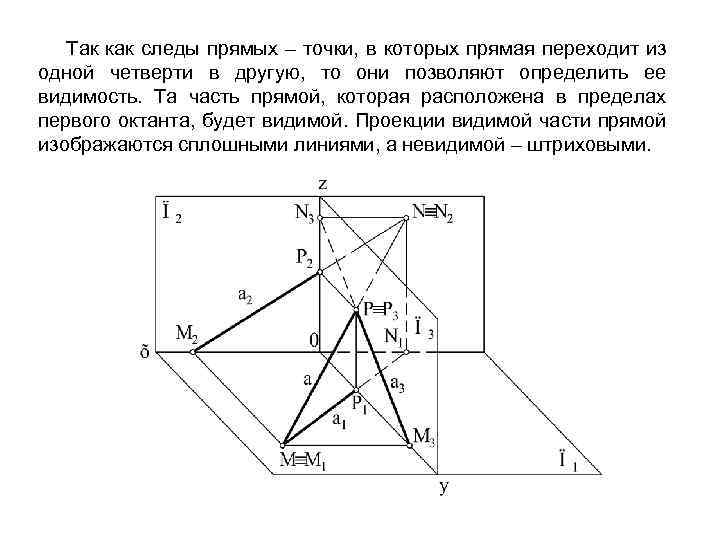
Так как следы прямых – точки, в которых прямая переходит из одной четверти в другую, то они позволяют определить ее видимость. Та часть прямой, которая расположена в пределах первого октанта, будет видимой. Проекции видимой части прямой изображаются сплошными линиями, а невидимой – штриховыми.

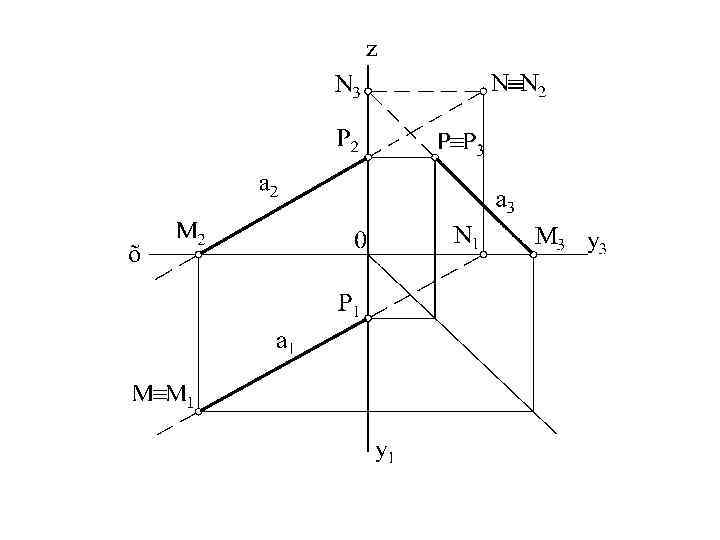
Профильный след Р находят как точку пересечения прямой ас профильной плоскостью проекций. Профильная проекция профильного следа прямой совпадает с самим следом, горизонтальная проекция этого следа Р 1 лежит на оси ОУ, а фронтальная проекция Р 2 лежит на оси ОZ. Чтобы построить профильный след прямой, продолжают фронтальную проекцию прямой а до пересечения с осью OZ. Отмечают точку Р 2 и из этой точки проводят перпендикуляр к оси OZ до пересечения с профильной проекцией прямой. Эта точка и будет искомым следом Р, с которым совпадает Р 3. Горизонтальная проекция Р 1 определяется как пересечение горизонтальной проекции прямой с осью ОУ.