ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ Лекция 9 Постановка задачи

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ Лекция 9

Постановка задачи проверки статистической гипотезы Понятие статистической гипотезы Статистическая проверка гипотез является вторым после статистического оценивания параметров распределения важнейшим разделом математической статистики. Определение. Статистической гипотезой называется предположение о виде распределения или о параметрах известных распределений.

Под статистической гипотезой понимают всякое высказывание о генеральной совокупности (случайной величине), проверяемое по выборке (по результатам наблюдений). Примеры. 1) Предположение о том, что генеральная совокупность имеет нормальный закон распределения. 2) Предположение о том, что дисперсии двух нормальных распределений и равны:

3) Предположение о том, что математические ожидания двух нормальных распределений и равны: Проверить статистическую гипотезу – это значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой. Определение. Гипотезу, выдвинутую для проверки ее согласия с выборочными данными, называют нулевой гипотезой и обозначают H 0. Определение. Альтернативной или конкурирующей гипотезой называется гипотеза, которая противоречит основной гипотезе и обозначается H 1.

Пример 1. При исследовании местности было произведено несколько проб древесины и вычислено, заболеваемости деревьев на 1 га равно что уровень . Через некоторое время произведено повторное исследование, и уровень заболеваемости деревьев стал , причем . Встает вопрос, расхождение случайно и связано с недостаточным числом измерений или закономерно и связано с изменением состояния леса.

Математическая постановка задачи. Х − состояние всех деревьев первоначально с математическим ожиданием числа заболевших деревьев − , Y – состояние всех деревьев через некоторое время с математическим ожиданием числа заболевших деревьев − .

Пример 2. Пусть в примере 1 за время между измерениями проводилась лечебная обработка деревьев и измерения показали, что . Встает вопрос, уменьшение показателя случайно и связано с недостаточным числом измерений или закономерно и связано с улучшением состояния леса вследствие проведенного лечения. Математическая постановка задачи.

Определение. Статистическая гипотеза называется простой, если она однозначно определяет закон распределения случайной величины. В противном случае, гипотеза называется сложной. Примеры простой гипотезы:

Примеры сложной гипотезы:

Пример. Радиостанция ведёт автоматическую передачу цифрового текста в течение 15 мкс. Работа происходит при наличии хаотической импульсной помехи, среднее число импульсов которой в одну секунду составляет 104. Для срыва передачи достаточно попадания 13 импульсов помехи в период радиопередачи. Число импульсов хаотической помехи во время радиопередачи текста – СВ Х. Классифицируем следующие гипотезы: Н 0(1): СВ Х распределена по закону Пуассона ; Н 0(2): СВ Х распределена по закону Пуассона с параметром = 0, 15; Н 0(3): СВ Х распределена по закону Пуассона, причём 0, 14 0, 16; Н 0(4): Р( 13 Х) = 0, 002 ; Н 0(5): вероятность срыва передачи зависит от сбоя в работе автономного источника электропитания. Н 0(1), Н 0(2), Н 0(3), Н 0(4) – статистические гипотезы: Н 0(1) – простая, непараметрическая, Н 0(2) - простая, параметрическая, Н 0(3)- сложная, параметрическая, Н 0(4)- сложная, непараметрическая, Н 0(5)- не является статистической гипотезой.

Ошибки принятия гипотез Принятие гипотезы в результате проверки не означает утверждения, что гипотеза верна. Это лишь означает, что результаты наблюдений не дают оснований её отвергнуть. Если основная гипотеза отвергается, то принимается альтернативная гипотеза. В процессе принятия гипотезы можно совершить ошибки 1 и 2 рода.

Ошибка 1 рода состоит в том, что будет отвергнута правильная нулевая гипотеза. Ошибка 2 рода состоит в том, что будет принята неправильная нулевая гипотеза. Вероятность допустить ошибку 1 рода, т. е. отвергнуть , когда она верна, называют уровнем значимости: Вероятность совершить ошибку 2 рода обозначается причем . ,

Вероятность не допустить ошибку 2 рода, т. е. отвергнуть гипотезу , когда она неверна, называется мощностью критерия: принимается верна неверна Решение правильное Ошибка 2 рода отвергается Ошибка 1 рода Решение правильное

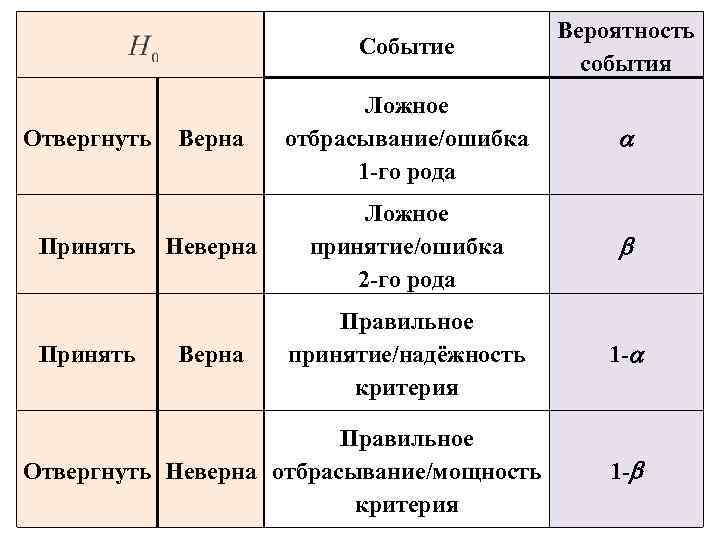Событие Отвергнуть Принять Вероятность события Верна Ложное отбрасывание/ошибка 1 -го рода Неверна Ложное принятие/ошибка 2 -го рода Верна Правильное принятие/надёжность критерия 1 - Правильное Отвергнуть Неверна отбрасывание/мощность критерия 1 -

Ошибки могут иметь разные последствия. Вероятность задается заранее, при этом обычно: 0, 1; 0, 05; 0, 001; 0, 005. Чем серьезнее последствия ошибки первого рода, тем меньше должен быть уровень значимости. Статистический критерий и критическая область Статистический критерий – это случайная величина, построенная по элементам выборки, точное или приближенное распределение которой известно, и по значению которого принимается решение о принятии или отклонении основной гипотезы .

Пусть К – статистический критерий гипотезы . Замечание. В дальнейшем, в зависимости от вида распределения критерия будут использоваться обозначения: - для нормального распределении - для распределения Фишера, - для распределения Стьюдента. Область принятия гипотезы – это множество значений критерия, при попадании в которое Kв основную гипотезу следует принять. Критические точки Kкр – точки, отделяющие область принятия гипотезы от критической области.

• Если принять оснований отклонить • если , отклонить принять . Критическая область бывает : - односторонней (правосторонней или левосторонней) - двусторонней. (нет и

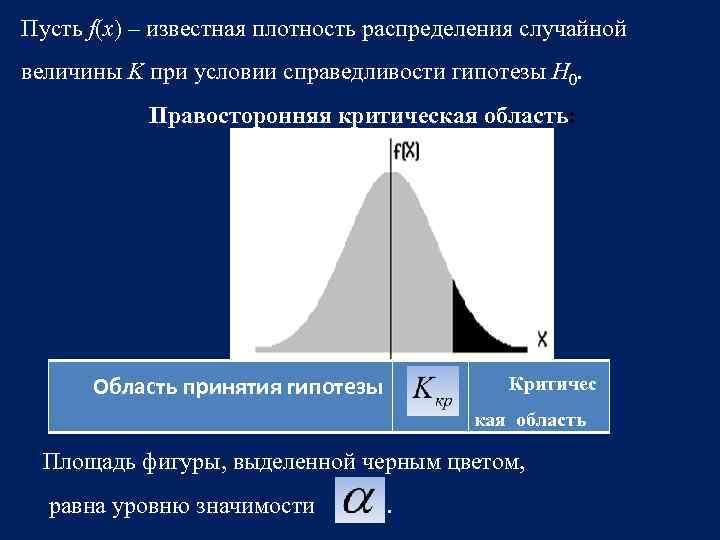Пусть f(x) – известная плотность распределения случайной величины K при условии справедливости гипотезы H 0. Правосторонняя критическая область: Область принятия гипотезы Критичес кая область Площадь фигуры, выделенной черным цветом, равна уровню значимости .

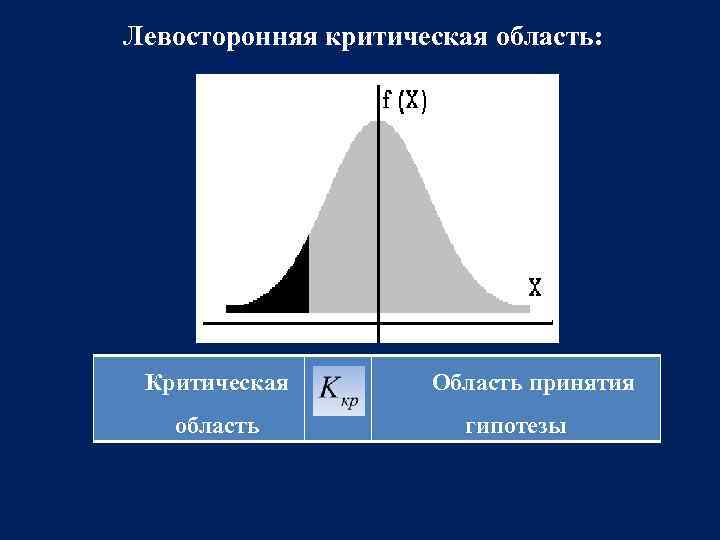Левосторонняя критическая область: Критическая область Область принятия гипотезы

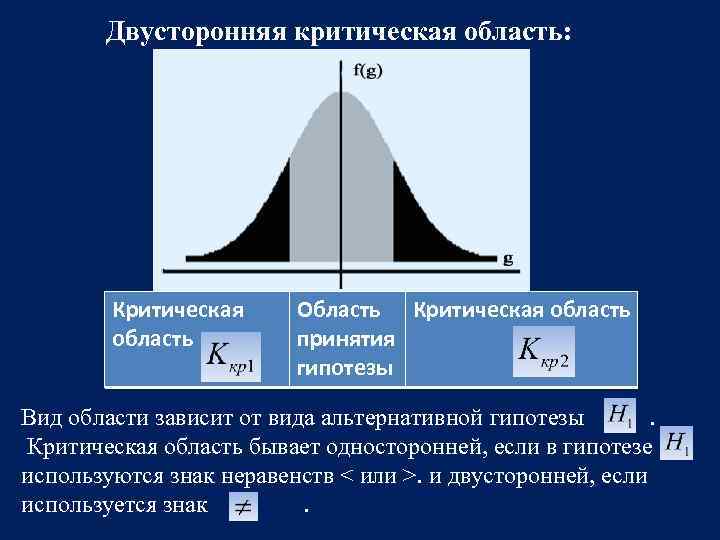Двусторонняя критическая область: Критическая область Область Критическая область принятия гипотезы Вид области зависит от вида альтернативной гипотезы. Критическая область бывает односторонней, если в гипотезе используются знак неравенств < или >. и двусторонней, если используется знак.

ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ На практике задача сравнения дисперсий возникает, если требуется сравнить точность приборов, инструментов, методов измерений, технологий. Очевидно, предпочтительнее взять тот прибор, инструмент и т. п. , который обеспечивает наименьшее рассеяние результатов измерений, т. е. наименьшую дисперсию. Проведем измерения на двух приборах. Пусть все возможные измерения первым прибором − Х и этим прибором проведено измерений , и по ним вычислена − оценка .

Пусть все возможные измерения первым прибором − Y и этим прибором проведено измерений, и по ним вычислена − оценка , причем . Требуется по выборочным средним и заданном проверить значимость этого различия. Краткое условие: Х: , Y: причем . Сформулируем гипотезу:

Зададим или в зависимости от конкретной задачи. Вычислим . где - большая дисперсия, а - меньшая дисперсия. Соответствующая случайная величина F − статистический критерий данной задачи − имеет распределение Фишера – Снедекора. Если , то выборочное значение критерия . Критическая область - правосторонняя.

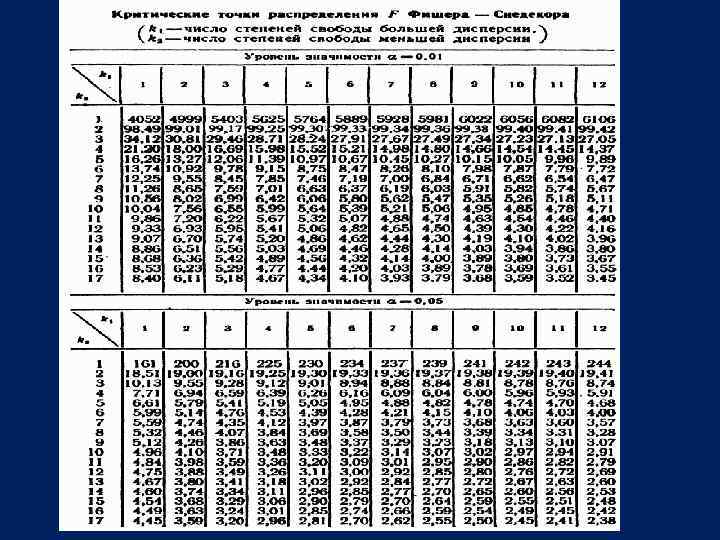
Для определения где найдем степени свободы: - объем выборки с большей дисперсией - объем выборки с меньшей дисперсией Используется таблица 7 .