Protein Structural Prediction Structure Determines Function The

Protein Structural Prediction

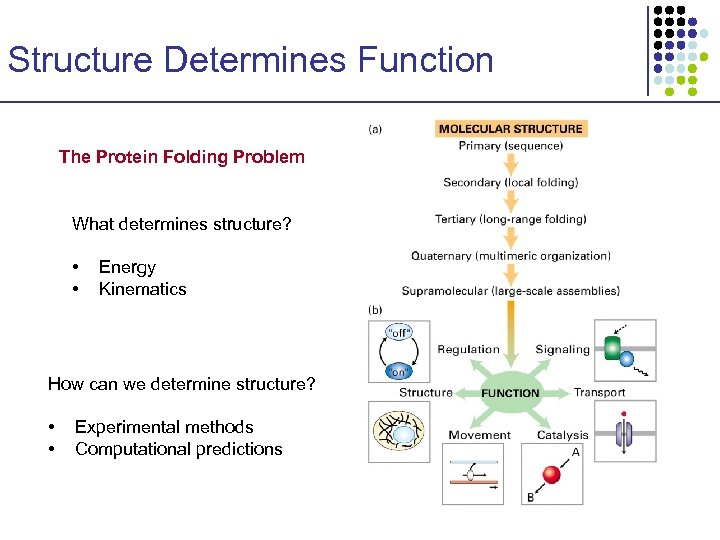Structure Determines Function The Protein Folding Problem What determines structure? • • Energy Kinematics How can we determine structure? • • Experimental methods Computational predictions

Protein Structure Prediction • ab initio § Use just first principles: energy, geometry, and kinematics • Homology § Find the best match to a database of sequences with known 3 Dstructure • Threading • Meta-servers and other methods

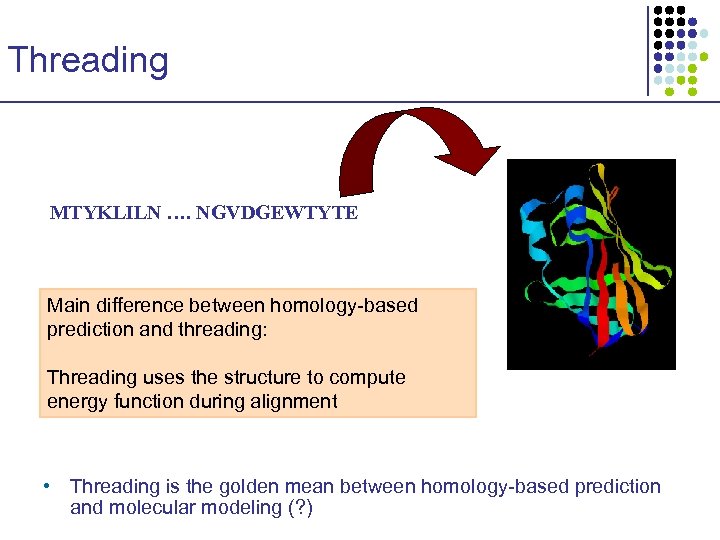Threading MTYKLILN …. NGVDGEWTYTE Main difference between homology-based prediction and threading: Threading uses the structure to compute energy function during alignment • Threading is the golden mean between homology-based prediction and molecular modeling (? )

Threading – Overview • Build a structural template database • Define a sequence–structure energy function • Apply a threading algorithm to query sequence • Perform local refinement of secondary structure • Report best resulting structural model

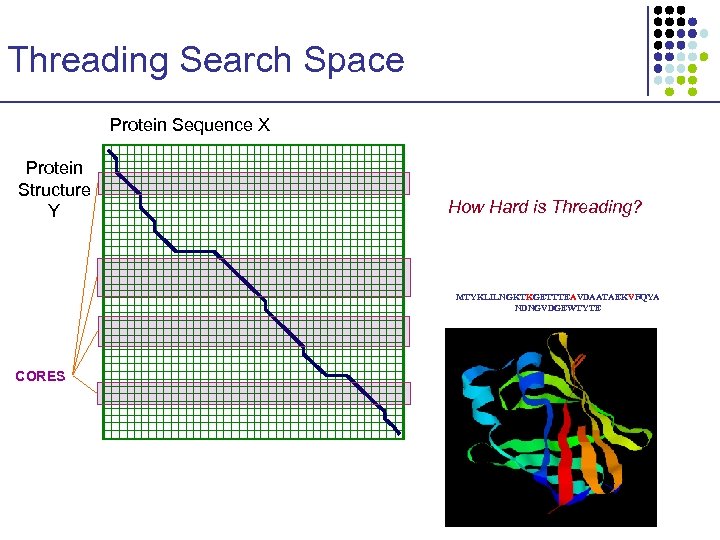
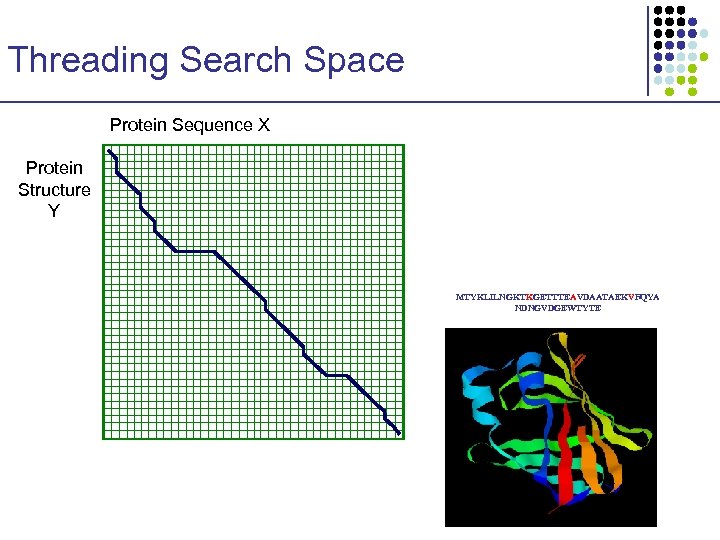Threading Search Space Protein Sequence X Protein Structure Y MTYKLILNGKTKGETTTEAVDAATAEKVFQYA NDNGVDGEWTYTE

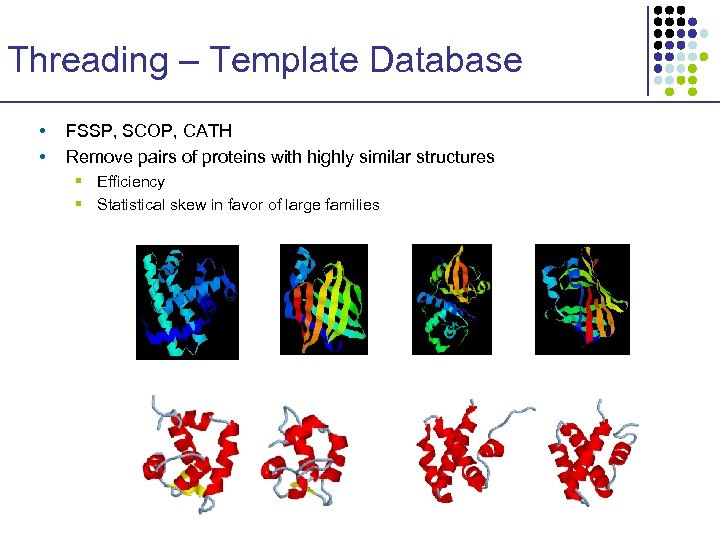Threading – Template Database • • FSSP, SCOP, CATH Remove pairs of proteins with highly similar structures § Efficiency § Statistical skew in favor of large families

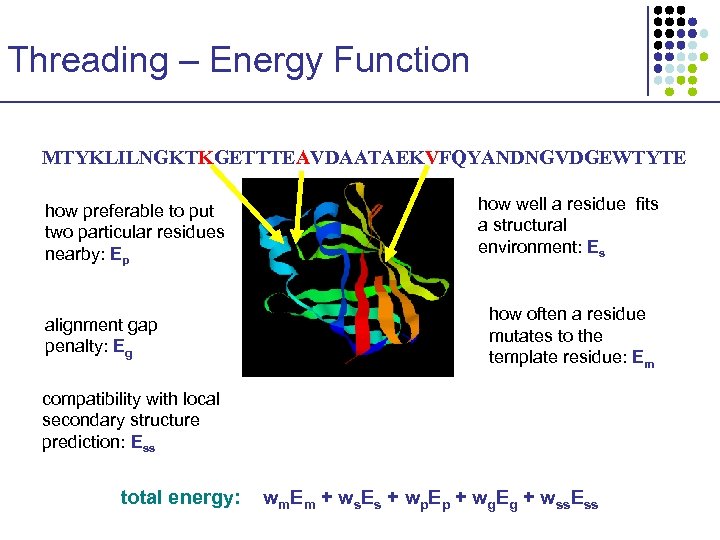Threading – Energy Function MTYKLILNGKTKGETTTEAVDAATAEKVFQYANDNGVDGEWTYTE how preferable to put two particular residues nearby: Ep alignment gap penalty: Eg how well a residue fits a structural environment: Es how often a residue mutates to the template residue: Em compatibility with local secondary structure prediction: Ess total energy: wm. Em + ws. Es + wp. Ep + wg. Eg + wss. Ess

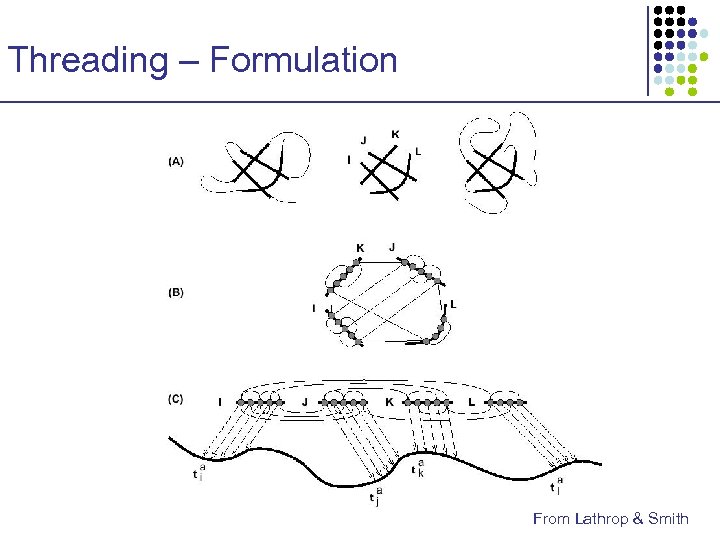
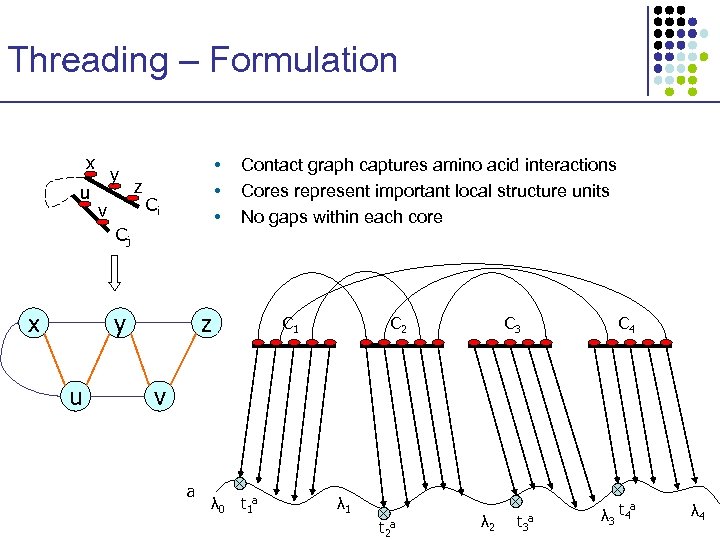Threading – Formulation x u y v z • • • Ci Cj x y u Contact graph captures amino acid interactions Cores represent important local structure units No gaps within each core z C 1 C 2 C 3 C 4 v a λ 0 t 1 a λ 1 t 2 a λ 2 t 3 a λ 3 t 4 a λ 4

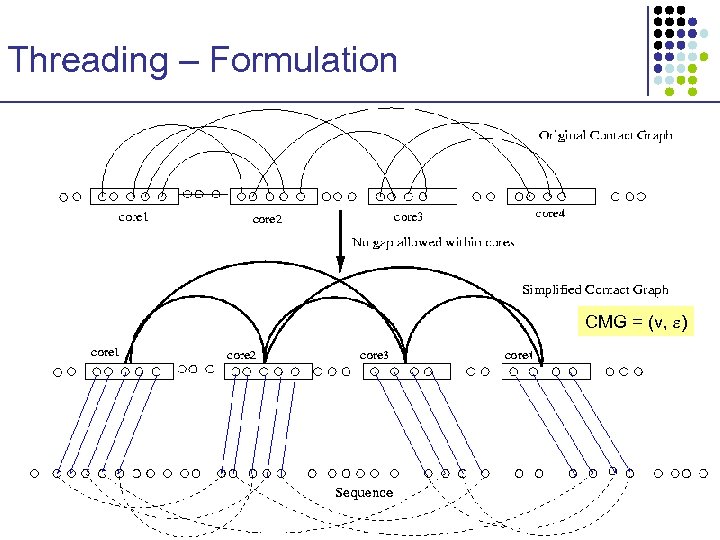Threading – Formulation CMG = (v, )

Threading – Formulation From Lathrop & Smith

Threading Search Space Protein Sequence X Protein Structure Y How Hard is Threading? MTYKLILNGKTKGETTTEAVDAATAEKVFQYA NDNGVDGEWTYTE CORES

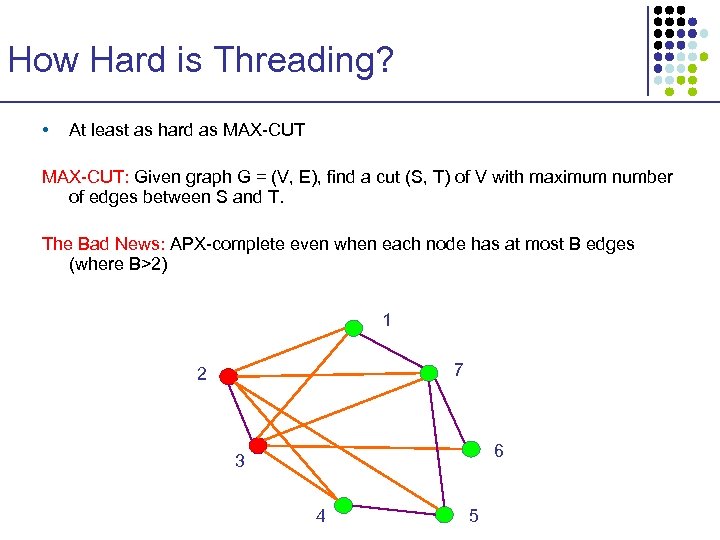How Hard is Threading? • At least as hard as MAX-CUT: Given graph G = (V, E), find a cut (S, T) of V with maximum number of edges between S and T. The Bad News: APX-complete even when each node has at most B edges (where B>2) 1 7 2 6 3 4 5

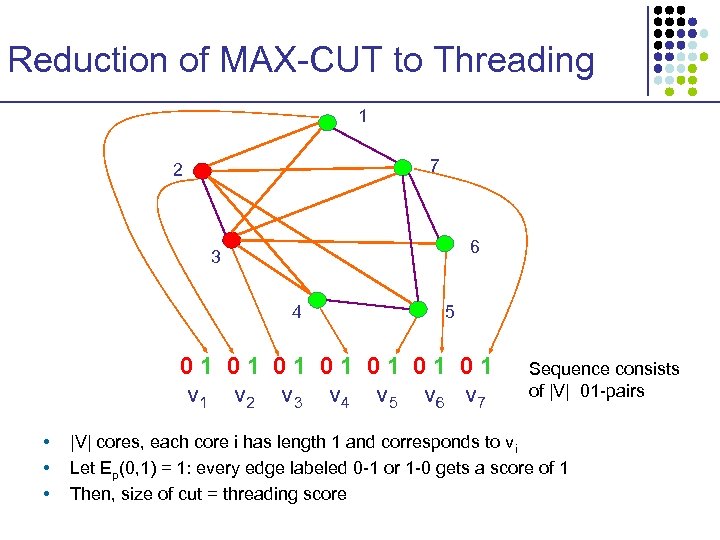Reduction of MAX-CUT to Threading 1 7 2 6 3 4 5 01 01 v 2 v 3 v 4 v 5 v 6 v 7 • • • Sequence consists of |V| 01 -pairs |V| cores, each core i has length 1 and corresponds to vi Let Ep(0, 1) = 1: every edge labeled 0 -1 or 1 -0 gets a score of 1 Then, size of cut = threading score

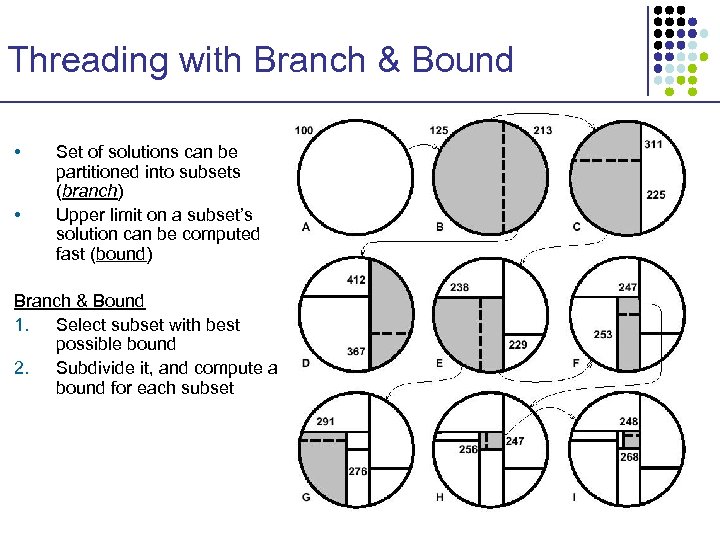Threading with Branch & Bound • • Set of solutions can be partitioned into subsets (branch) Upper limit on a subset’s solution can be computed fast (bound) Branch & Bound 1. Select subset with best possible bound 2. Subdivide it, and compute a bound for each subset

Threading with Branch & Bound • Key to this algorithm is tradeoff on lower bound § efficient § tight

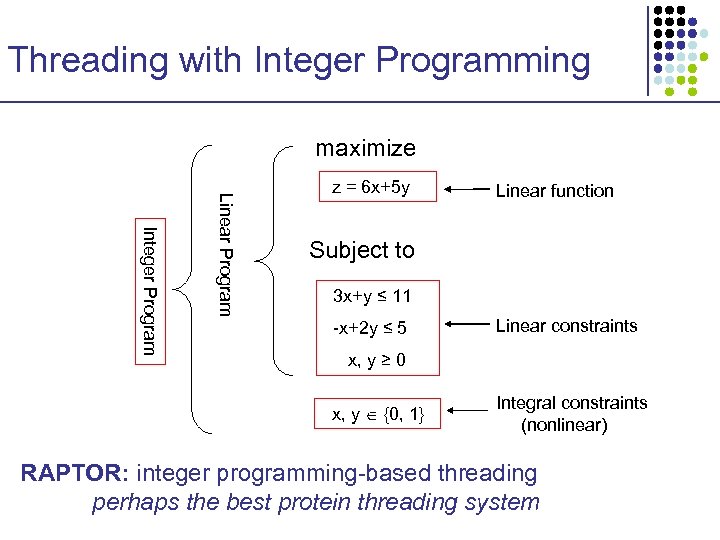Threading with Integer Programming maximize Integer Program Linear Program z = 6 x+5 y Linear function Subject to 3 x+y ≤ 11 -x+2 y ≤ 5 Linear constraints x, y ≥ 0 x, y {0, 1} Integral constraints (nonlinear) RAPTOR: integer programming-based threading perhaps the best protein threading system

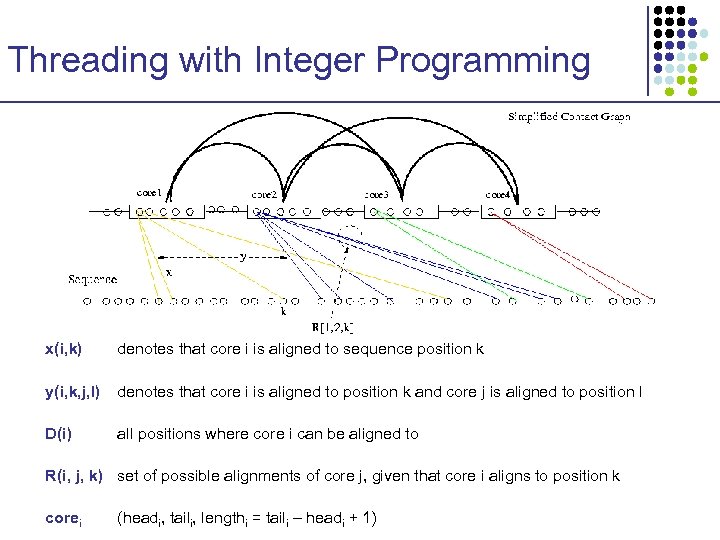Threading with Integer Programming x(i, k) denotes that core i is aligned to sequence position k y(i, k, j, l) denotes that core i is aligned to position k and core j is aligned to position l D(i) all positions where core i can be aligned to R(i, j, k) set of possible alignments of core j, given that core i aligns to position k corei (headi, taili, lengthi = taili – headi + 1)

Threading with Integer Programming Cores are aligned in order Each y variable is 1 if and only if its two x variables are 1 – x and y represent exactly the same threading Each core has only one alignment position

Energy Function is Linear • Sequence substitution score • Fitness of aa in each position (example, hydrophobicity) • Agreement with secondary structure prediction • Pairwise interaction between two cores • Gap between two successive cores

LP Relaxation and (again) Branch & Bound 1. Relax the integral constraint, to x(i, j), y(i, k, j, l) 0 2. Solve the LP using a standard method (RAPTOR uses IBM’s OSL) 3. If resulting solution is integral, done 4. Else, select one non-integral variable (heuristically), and generate two subproblems by setting it to 0, and 1 -- use Branch & Bound In practice, in RAPTOR only 1% of the instances in the test database required step 4; almost all solutions are integral !!!

CAFASP GOAL The goal of CAFASP is to evaluate the performance of fully automatic structure prediction servers available to the community. In contrast to the normal CASP procedure, CAFASP aims to answer the question of how well servers do without any intervention of experts, i. e. how well ANY user using only automated methods can predict protein structure. CAFASP assesses the performance of methods without the user intervention allowed in CASP.

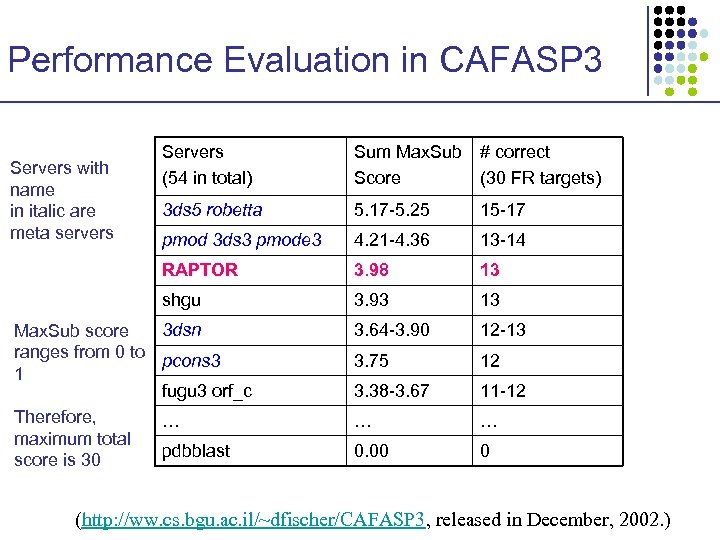Performance Evaluation in CAFASP 3 Sum Max. Sub # correct Score (30 FR targets) 3 ds 5 robetta 5. 17 -5. 25 15 -17 pmod 3 ds 3 pmode 3 4. 21 -4. 36 13 -14 RAPTOR 3. 98 13 shgu Servers with name in italic are meta servers Servers (54 in total) 3. 93 13 3. 64 -3. 90 12 -13 3. 75 12 3. 38 -3. 67 11 -12 … … 0. 00 0 3 dsn Max. Sub score ranges from 0 to pcons 3 1 fugu 3 orf_c Therefore, … maximum total pdbblast score is 30 (http: //ww. cs. bgu. ac. il/~dfischer/CAFASP 3, released in December, 2002. )

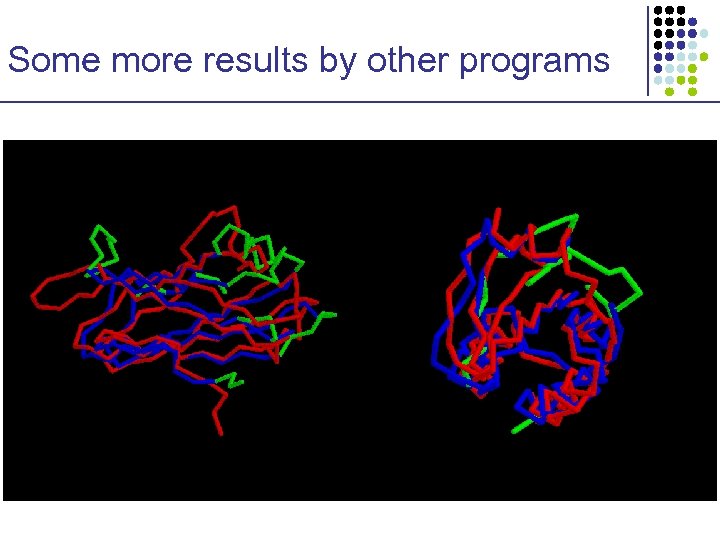
One structure where RAPTOR did best Red: true structure Blue: correct part of prediction Green: wrong part of prediction • Target Size: 144 • Super-imposable size within 5 A: 118 • RMSD: 1. 9

Some more results by other programs

Some more results by other programs

Some more results by other programs

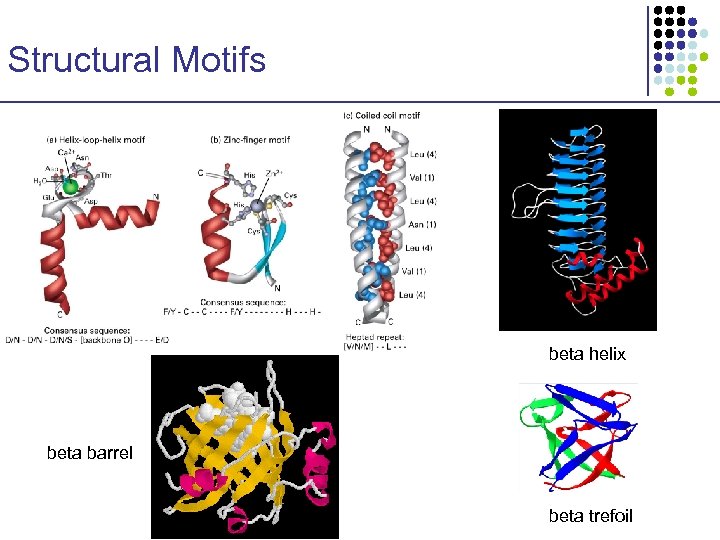Structural Motifs beta helix beta barrel beta trefoil

Structural Motif Recognition • Secondary Structure Prediction § Find the helices, sheets, loops in a protein sequence • Given an amino acid residue sequence, does it fold as a § § Coiled Coil? helix? barrel? Zinc finger? • Intermediate goals towards folding • Useful information about the function of a protein • More amenable to sequence analysis, than full fold prediction

Structural Motif Recognition 1. Collect a database of known motifs and corresponding amino acid subsequences 2. Devise a method/model to “match” a new sequence to existing motif database 3. Verify computationally on a test set (divide database into training and testing subsets) 4. Verify in lab

Structural Motif Recognition Methods • Alignment • Neural Nets • Hidden Markov Models • Threading • Profile-based Methods • Other Statistical Methods

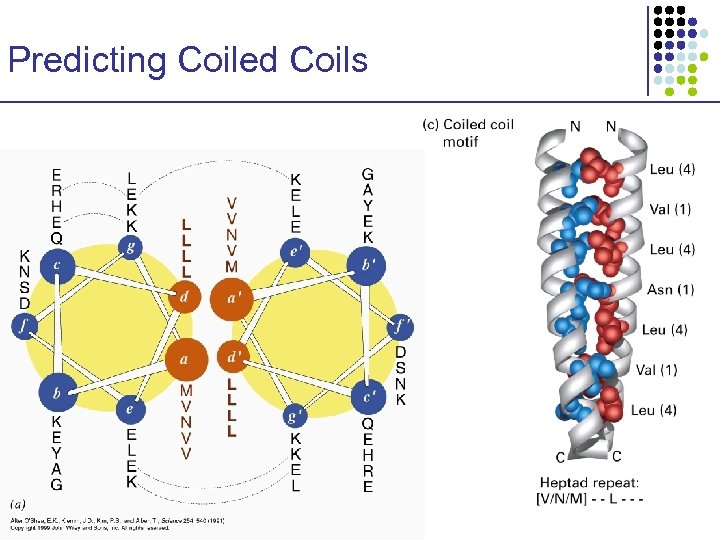Predicting Coiled Coils

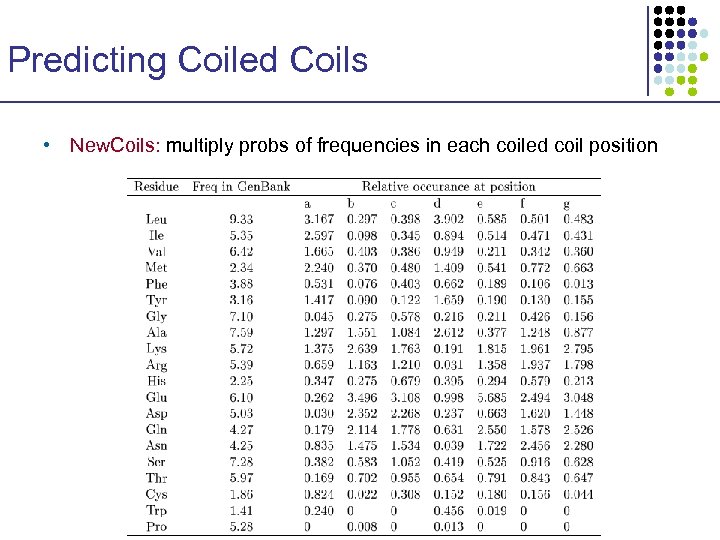Predicting Coiled Coils • New. Coils: multiply probs of frequencies in each coiled coil position

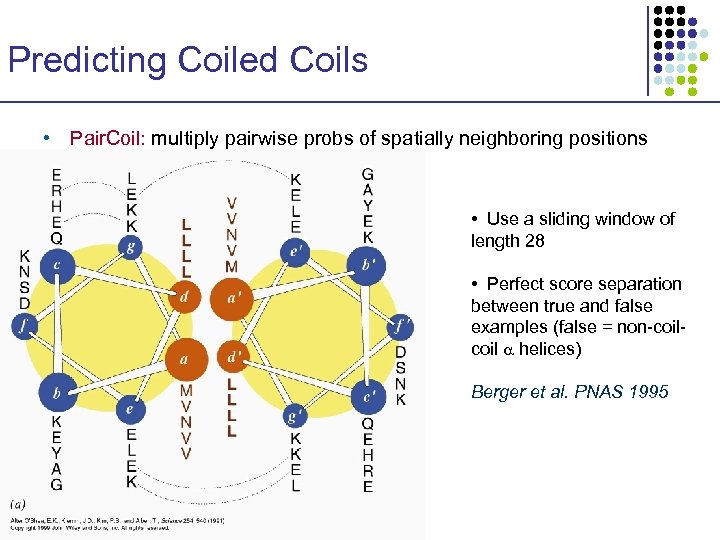Predicting Coiled Coils • Pair. Coil: multiply pairwise probs of spatially neighboring positions • Use a sliding window of length 28 • Perfect score separation between true and false examples (false = non-coil helices) Berger et al. PNAS 1995

Predicting helices • Helix composed of three parallel sheets • Very few solved structures, very different from one another • Absent in eukaryotes! § Probably evolved subsequent to prok/euk split

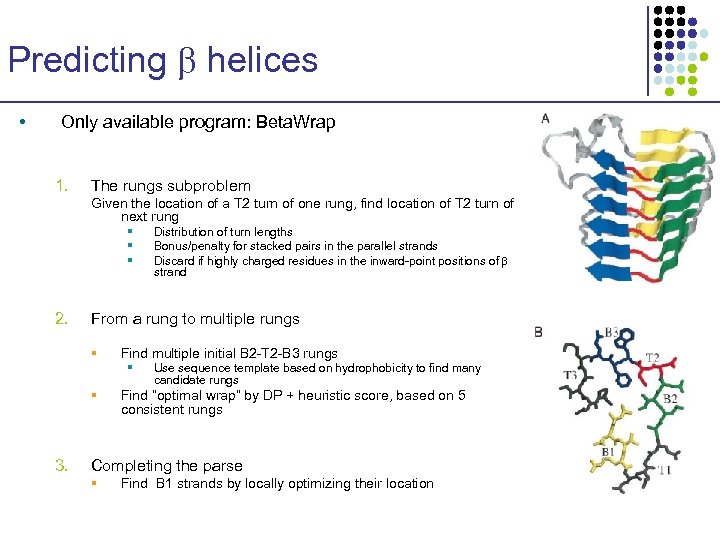Predicting helices • Only available program: Beta. Wrap 1. The rungs subproblem Given the location of a T 2 turn of one rung, find location of T 2 turn of next rung § § § 2. From a rung to multiple rungs § Find multiple initial B 2 -T 2 -B 3 rungs § § 3. Distribution of turn lengths Bonus/penalty for stacked pairs in the parallel strands Discard if highly charged residues in the inward-point positions of strand Use sequence template based on hydrophobicity to find many candidate rungs Find “optimal wrap” by DP + heuristic score, based on 5 consistent rungs Completing the parse § Find B 1 strands by locally optimizing their location

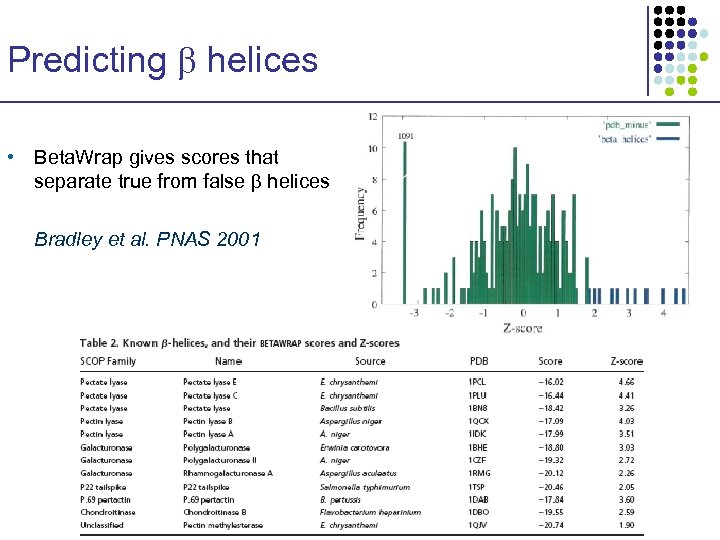Predicting helices • Beta. Wrap gives scores that separate true from false helices Bradley et al. PNAS 2001

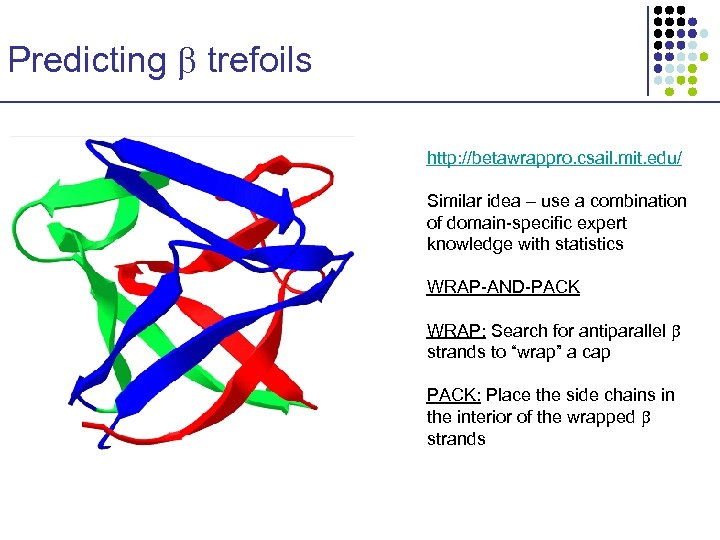Predicting trefoils http: //betawrappro. csail. mit. edu/ Similar idea – use a combination of domain-specific expert knowledge with statistics WRAP-AND-PACK WRAP: Search for antiparallel strands to “wrap” a cap PACK: Place the side chains in the interior of the wrapped strands

Predicting Secondary Structure • Given amino acid sequence, classify positions into helices, strands, or loops • In general, harder than protein motif identification • Best methods rely on Neural Networks § Similarly good separation can be achieved by SVMs PSIPRED 1. 2. 3. Given a sequence x, generate profile using PSI-BLAST Pass the profile to a pre-trained NN Output classification: helix / strand / loops

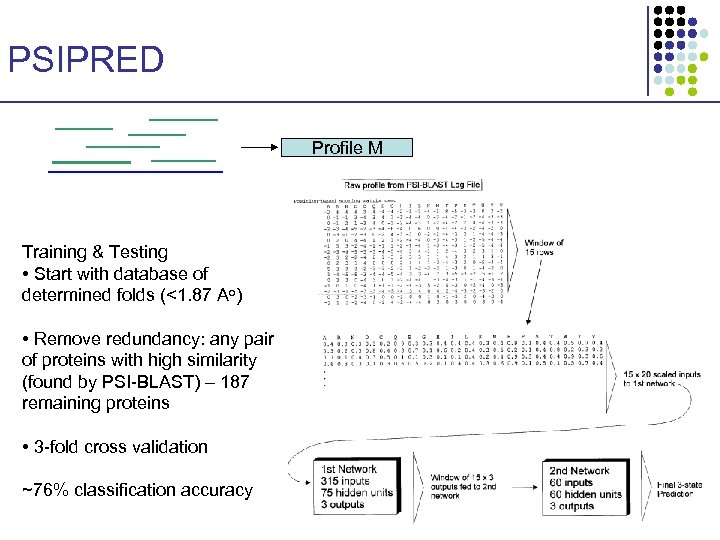PSIPRED Profile M Training & Testing • Start with database of determined folds (<1. 87 Ao) • Remove redundancy: any pair of proteins with high similarity (found by PSI-BLAST) – 187 remaining proteins • 3 -fold cross validation ~76% classification accuracy

PSIPRED server PSIPREDICTION RESULTS Conf: Confidence (0=low, 9=high) Pred: Predicted secondary structure (H=helix, E=strand, C=coil) AA: Target sequence # PSIPRED HFORMAT (PSIPRED V 2. 3 by David Jones) Conf: 988878877765688766579 Pred: CCCCCCCCCCCCCC AA: PEPTIDEPEPTIDE Conf: 998888872100111210012112359 Pred: CCCCCCHHHHCCCC AA: PTYPTYPTXXXXXXTEETEET PSIPREDICTION RESULTS Conf: Confidence (0=low, 9=high) Pred: Predicted secondary structure (H=helix, E=strand, C=coil) AA: Target sequence # PSIPRED HFORMAT (PSIPRED V 2. 3 by David Jones) Conf: 988888600148777777885001487777778842003789 Pred: CCCCCCCCEECCCCCCCCCCC AA: PPEEPPTTIIDDEEPPEEPPTTIIDDEE Conf: 91025687432236422336410232027743223653334679 Pred: CCCCCCCCCCCCEEEECCCCCCCCC AA: THISISAPRXTEINSEQXENCE

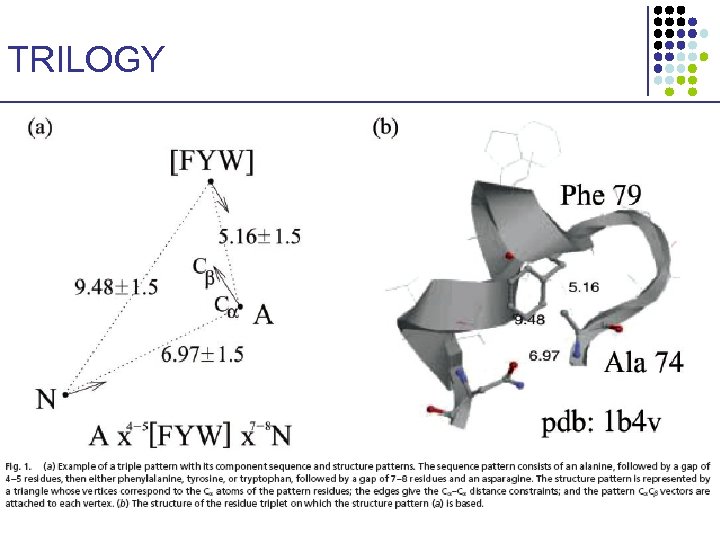
TRILOGY: Sequence–Structure Patterns • • Identify short sequence–structure patterns 3 amino acids Find statistically significant ones (hypergeometric distribution) § Correct for multiple trials • These patterns may have structural or functional importance 1. 2. Pseq: Pstr: • Start with short patterns of 3 amino acids R 1 xa-b. R 2 xc-d. R 3 3 C – C distances, & 3 C – C vectors {V, I, L, M}, {F, Y, W}, {D, E}, {K, R, H}, {N, Q}, {S, T}, {A, G, S} • Extend to longer patterns Bradley et al. PNAS 99: 8500 -8505, 2002

TRILOGY

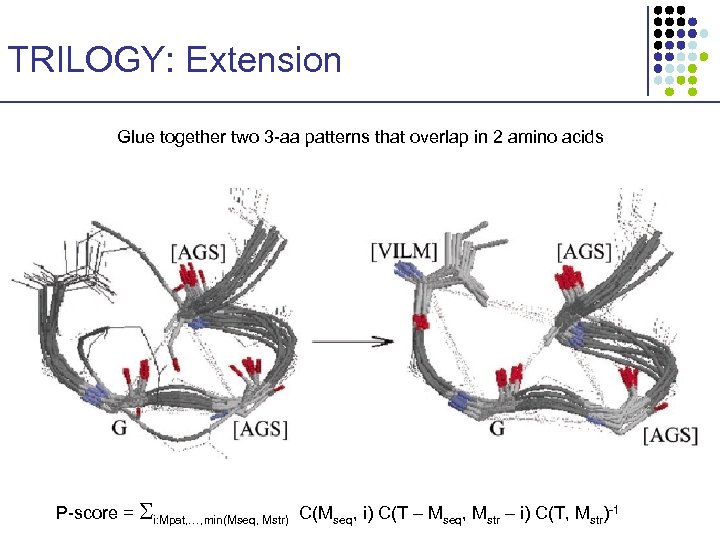TRILOGY: Extension Glue together two 3 -aa patterns that overlap in 2 amino acids P-score = i: Mpat, …, min(Mseq, Mstr) C(Mseq, i) C(T – Mseq, Mstr – i) C(T, Mstr)-1

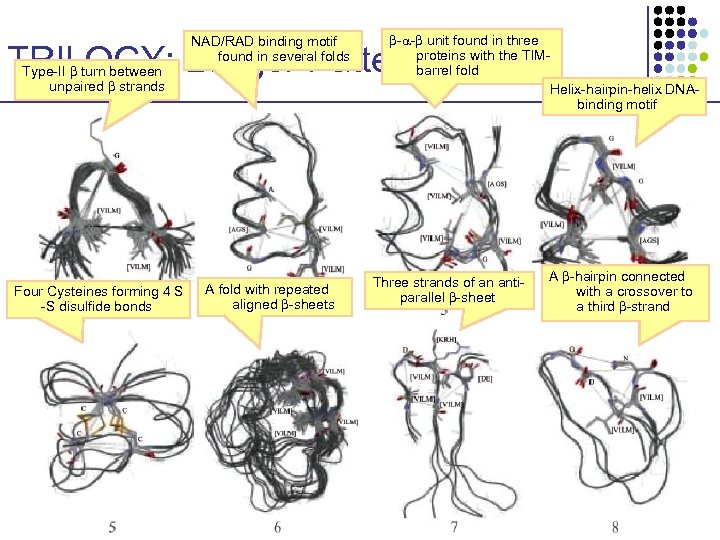NAD/RAD binding motif found in several folds - - unit found in three proteins with the TIMbarrel fold Helix-hairpin-helix DNAbinding motif TRILOGY: Longer Patterns Type-II turn between unpaired strands Four Cysteines forming 4 S -S disulfide bonds A fold with repeated aligned -sheets Three strands of an antiparallel -sheet A -hairpin connected with a crossover to a third -strand

Small Libraries of Structural Fragments for Representing Protein Structures

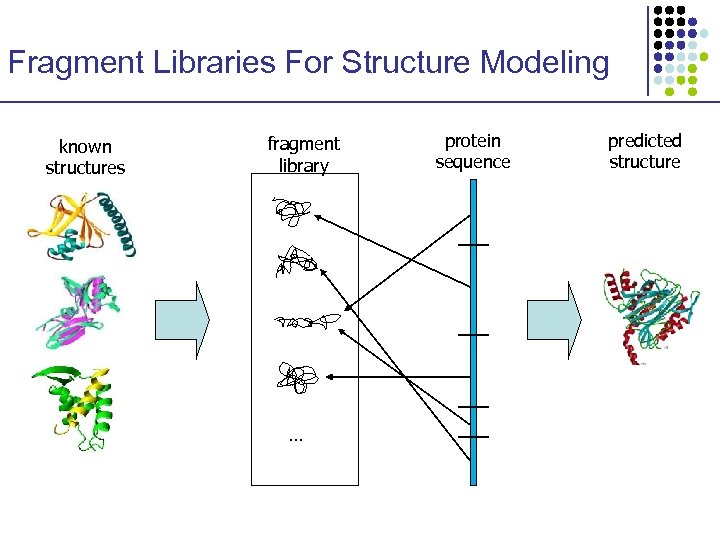Fragment Libraries For Structure Modeling known structures fragment library … protein sequence predicted structure

Small Libraries of Protein Fragments Kolodny, Koehl, Guibas, Levitt, JMB 2002 Goal: Small “alphabet” of protein structural fragments that can be used to represent any structure 1. 2. 3. Generate fragments from known proteins Cluster fragments to identify common structural motifs Test library accuracy on proteins not in the initial set f

Small Libraries of Protein Fragments Dataset: 200 unique protein domains with most reliable & distinct structures from SCOP § • 36, 397 residues Divide each protein domain into consecutive fragments beginning at random initial position Library: Four sets of backbone fragments § • 4, 5, 6, and 7 -residue long fragments Cluster the resulting small structures into k clusters using c. RMS, and applying k-means clustering with simulated annealing § § f Cluster with k-means Iteratively break & join clusters with simulated annealing to optimize total variance Σ(x – μ)2

Evaluating the Quality of a Library • Test set of 145 highly reliable protein structures (Park & Levitt) • Protein structures broken into set of overlapping fragments of length f • Find for each protein fragment the most similar fragment in the library (c. RMS) Local Fit: Average c. RMS value over all fragments in all proteins in the test set Global Fit: Find “best” composition of structure out of overlapping fragments § Complexity is O(|Library|N) § Greedy approach extends the C best structures so far from pos’n 1 to N

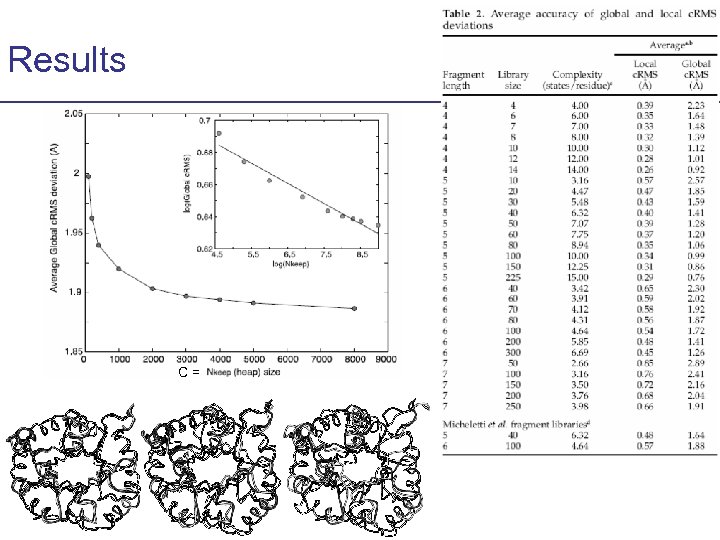Results C=