ПРОСТЫЕ ЧИСЛА ФЕРМА Если число с является

ПРОСТЫЕ ЧИСЛА ФЕРМА

Если число с является произведением двух чисел а и b (с = a∙b), мы называем числа а и b множителями или делителями числа с. Каждое число имеет тривиальное (простейшее) разложение на множители: с = с∙ 1 = 1∙с. Соответственно числа 1 и с мы называем тривиальными делителями числа с. Любое число с>1, у которого существует нетривиальное разложение на множители, называется составным. Если число, большее единицы, имеет только тривиальное разложение на множители, то оно называется простым. Среди первых ста чисел простыми являются следующие 25 чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, а все остальные числа, кроме 1, являются составными.

Пьер Ферма (1601— 1665)французский юрист, который был одновременно и выдающимся математиком. Он получил великолепное гуманитарное образование и был выдающимся знатоком искусства и литературы. Всю жизнь он проработал на государственной службе, последние лет был советником местного Пьер Ферма (1601 17 — 1665) парламента в Тулузе. К математике его влекла бескорыстная и возвышенная любовь, и именно эта наука дала ему всё, что может дать человеку любовь: упоение красотой, наслаждение и счастье. В те годы не было ещё математических журналов, и Ферма почти ничего не напечатал при жизни. Посредством переписки со своими современниками некоторые его достижения становились известными.

ПРОСТЫЕ ЧИСЛА ФЕРМА Общая формула для простых чисел Ферма Первыми пятью простыми числами Ферма являются

П. Ферма считал, что F 5=429496729 простое число, так как не смог найти для него делитель. В том же 1640 году Ферма доказал свою малую теорему: "Для всякого простого числа p и натурального x число xp-1 -1 делится на p". Если не делится, следовательно, p не является простым числом. Используя свою теорему, Ферма мог бы проверить 5 -е число, использовав всего 32 операции возведения в квадрат по модулю 232+1 получил бы число 3029026160 и этим доказал, что 5 -е число составное, даже не находя его делителей.

Леонард Эйлер опроверг утверждение Ферма, указав, что число F 5 раскладывается на множители: 641 и 6700417. Эйлер доказал, что всякий делитель числа Ферма имеет вид: k∙ 2 m+2+1 Леонард Эйлер (1707 -1783) Таким образом, Эйлер проверял всего 10 делителей вида 64 k+1.

В 1878 Эдуард Люка усилил этот результат: каждый делитель числа Ферма имеет вид: при любом k. Эдуард Люка (1842 -1891) После того, как Леонард Эйлер показал, что пятое число Ферма не является простым, предположение о том, что все числа Ферма простые было сдано в архив неоправдавшихся математических гипотез.

О ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКАХ Правильным многоугольником называется многоугольник, вершины которого лежат на некоторой окружности на одинаковых расстояниях друг от друга. Если у правильного многоугольника n вершин, то мы называем его правильным n-угольником. Если мы проведем n радиусов, соединяющих центр окружности с вершинами, то получим n центральных углов величиной каждый. Если можно построить угол, имеющий эту величину, то можно построить и сам многоугольник.

Древние греки очень хотели найти методы построения правильных многоугольников с помощью циркуля и линейки. Разумеется, они умели строить простейшие из них — равносторонний треугольник и квадрат. С помощью повторного деления пополам центрального угла они могли также построить правильные многоугольники с 8, 16, 32, . . . , и 6, 12, 24, . . , вершинами. Кроме того, они умели строить правильный пятиугольник и, следовательно, также правильные многоугольники с 10, 20, 40, . . . вершинами

Был также получен еще один тип правильного многоугольника. Центральный угол в правильном 15 -угольнике равен и он может быть получен с помощью угла в 72°, соответствующего правильному пятиугольнику, и угла в 120° , соответствующего правильному треугольнику, если удвоить первый угол и вычесть из него второй. Следовательно, мы можем построить правильные многоугольники с 15, 30, 60, 120, . . . сторонами.

В 1801 году Карл-Фридрих Гаусс В опубликовал работу по теории чисел «Арифметические исследования» . В ней Гаусс: üуказал метод для построения циркулем и линейкой правильного 17 угольника; Карл-Фридрих üопределил для всех чисел n, какие n. Гаусс (1777 -1855) угольники могут быть построены таким образом, а какие нет. Гаусс показал, что правильный многоугольник с нечетным числом вершин может быть построен с помощью циркуля и линейки тогда и только тогда, когда число n является простым числом Ферма или произведением нескольких различных простых чисел Ферма.

ü Когда "королю математиков" Карлу Гауссу было всего 19 лет, он доказал, что с помощью циркуля и линейки можно построить правильный n- угольник для простого n тогда и только тогда, когда - простое число. ü Таким образом, можно построить 3, 5, 17, 257 и 65537 угольники. ü Сам Гаусс построил 17 -угольник. ü Решил на 80 страницах указал построение 257 угольника. ü В гёттингенской библиотеке в чемоданах больших размеров хранится способ построения правильного 65537 -угольника, выполненное неким Гермесом.

Очевидно, треугольник и пятиугольник могут быть построены, в то время как семиугольник не может быть построен, так как 7 не является простым числом Ферма. Не может быть построен и девятиугольник, так как 9 = 3∙ 3 является произведением двух равных простых чисел Ферма. Открытие Гаусса, естественно, возродило интерес к числам Ферма. За последнее столетие были предприняты поистине героические поиски «вручную» , без помощи машин, новых простых чисел Ферма. В настоящее время эти вычисления ведутся с все возрастающей скоростью при помощи компьютера.

Проблема № 1. Существует ли бесконечно много простых чисел Ферма? Проблема № 2. Существует ли бесконечно много составных чисел Ферма? На сегодняшний день неизвестно, конечно или бесконечно количество простых чисел Ферма. Существуют весьма сильные аргументы как за одну, так и за другую гипотезу. Чтобы доказать, что число Ферма не простое, существует два принципиальных способа: 1 способ. Найти хотя бы один делитель. 2 способ. Воспользоваться детерминированным тестом Пепина. Теорема. Число Fm простое тогда и только тогда, когда 3 (Fm-1)/2 +1 делится на Fm.

Из-за большой редкости делителей и сложности их обнаружения каждый человек, нашедший новый делитель числа Ферма, попадает в историю математики. За три с половиной века поиска известно немногим более 200 делителей. На май 2001 года список их первооткрывателей включает 60 человек из разных стран мира.

Вот некоторые из них: Немецкий профессор Вилфрид Келлер ведет сегодня официальную статистику всех известных делителей чисел Ферма. В 1855 году немецкий астроном Томас Клаусен в письме к Гауссу сообщил о разложении 6 -го числа Ферма, но этот факт оставался более века неизвестным и еще три человека независимо, позже находили этот результат. Уральский самоучка священник-математик Иван Михеевич Первушин прославился открытием трех чисел. В 1903 году Вестерн за год титанической работы находит независимо пять новых делителей для различных чисел Ферма и после этого сообщает, что у любого числа Ферма не существует больше делителей меньше миллиона.

Ручным способом за 3 века было найдено лишь 16 делителей для чисел Ферма. Рафаэль Робинсон в начале 50 -х нашел 20 делителей на одном из первых компьютеров SWAC. Он один из первых показал очень хороший путь отыскания делителей на компьютерах. На сегодняшний день самым плодовитым искателем делителей для чисел Ферма является американский разработчик компьютерных систем Гари Гостин, который на суперкомпьютерах в разные годы нашел уже больше 6 -и десятков делителей. В 1993 году он приостановил свои вычисления. Один из ярых охотников за числами Ферма японец Тадаси Таура открыл 16 делителей.

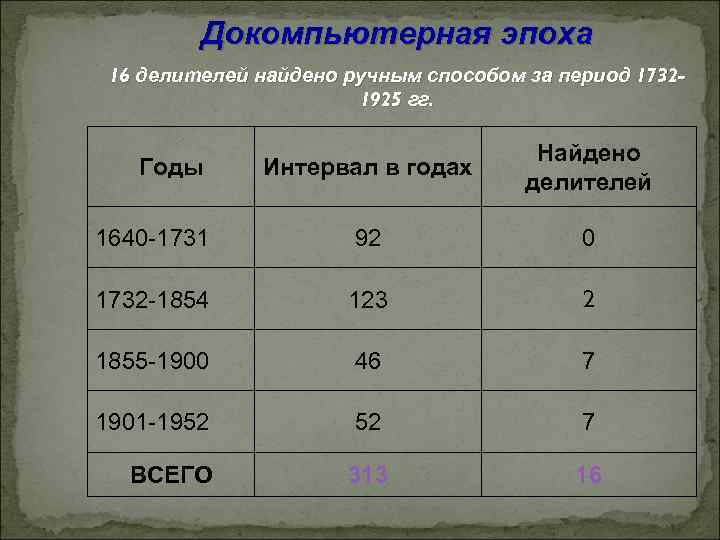Докомпьютерная эпоха 16 делителей найдено ручным способом за период 17321925 гг. Интервал в годах Найдено делителей 1640 -1731 92 0 1732 -1854 123 2 1855 -1900 46 7 1901 -1952 52 7 ВСЕГО 313 16 Годы

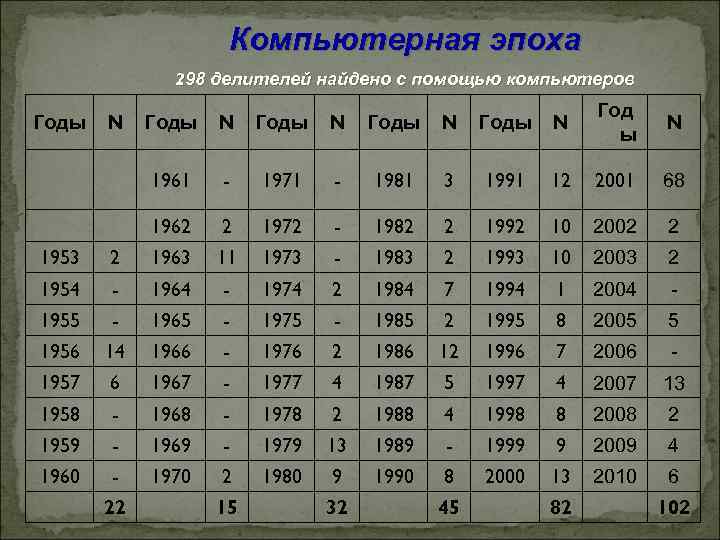Компьютерная эпоха 298 делителей найдено с помощью компьютеров N Годы N Год ы N - 1971 - 1981 3 1991 12 2001 68 1962 N N Годы 1961 Годы 2 1972 - 1982 2 1992 10 2002 2 Годы 1953 2 1963 11 1973 - 1983 2 1993 10 2003 2 1954 - 1964 - 1974 2 1984 7 1994 1 2004 - 1955 - 1965 - 1975 - 1985 2 1995 8 2005 5 1956 14 1966 - 1976 2 1986 12 1996 7 2006 - 1957 6 1967 - 1977 4 1987 5 1997 4 2007 13 1958 - 1968 - 1978 2 1988 4 1998 8 2008 2 1959 - 1969 - 1979 13 1989 - 1999 9 2009 4 1960 - 1970 2 1980 9 1990 8 2000 13 2010 6 22 15 32 45 82 102

Ø 206 делителей найдено с помощью компьютеров; Ø 222 делителя найдено за всю историю до мая 2001 года; Ø 12 апреля 2001 года немец Александр Крупа, используя программу MFAC Тони Форбеса обнаружил долгожданный делитель для особенного числа у математиков F 31. Вот этот делитель: 5463561471303∙ 2 +1=46931635677864055013377 Следующее число Ферма, характер которого не известен, – F 33.

Вывод: на сегодняшний день мы знаем судьбу всех чисел Ферма до F 32 включительно. Для большинства из этих чисел известны также их делители. Для разложения больших чисел наилучшим сегодня является ECM (метод эллиптических кривых), тесно связанный со стойкой криптографией и находящийся на переднем крае математической науки.

Многие величайшие математики увлекались этими забавными числами. Увлечение это не пропало и сегодня, особенно с возникновением компьютеров. В настоящее время эти вычисления ведутся с все возрастающей скоростью при помощи компьютера, однако до сих пор результаты были отрицательными. Ни одного нового простого числа Ферма пока не найдено. И сейчас многие математики склонны считать, что их больше нет.

Проблема № 1. Существует ли еще хотя бы одно простое число Ферма, отличное от 5 -ти известных? Проблема № 2. Существует ли бесконечно много составных чисел Ферма?

Список используемой литературы: Дурман Л. Гонки по вертикали, или Числа Ферма от Эйлера до наших дней // Компьютерра, 2001, № 16. Кирилов А. О правильных многоугольниках, функции Эйлера и числах Ферма // Квант, 1977, № 7, с. 2 -9. Оре О. Простые числа Ферма // Квант, 1979, № 12. – с. 31 -33. Историческая таблица всех людей, занимавшихся и занимающихся числами Ферма – http: //www. fermatsearch. org/history. htm