Пространство 1 Пространство Тема сегодняшней лекции связана

Пространство 1

Пространство Тема сегодняшней лекции связана с формированием представлений человека о пространстве 2

Представления о пространстве Пространство формировались по мере освоения человеком жизненно необходимых территорий. Древнейшая область математики – геометрия ( - землемерие) - наука о способах измерения площадей, объемов, расстояний. 3

n n n прямая есть такая линия, которая одинаково расположена относительно своих частей; поверхность есть то, что имеет только длину и ширину; плоскость есть поверхность, которая одинаково расположена по отношению ко всем прямым, лежащим в этой плоскости. Пространство 4

n n n От всякой точки до всякой точки можно провести прямую. Ограниченную прямую можно непрерывно продолжать по прямой. Из всякого центра всяким раствором может быть описан круг. Все прямые углы равны между собой. Параллельные линии нигде не пересекаются Пространство 5

«одинаково расположена» - характеристики окружающего Пространство физического мира. Они выявляют некоторые характерные свойства реальных объектов: натянутой струны или луча света, гладкой поверхности и т. п. . 6

Пространство n Евклидово ли пространство? n Не искривлено ли оно? n Не пересекутся ли параллельные линии на бесконечности? n Всегда ли сумма углов треугольника 180 о? 7

могут замкнуть часть пространства. Пространство n То есть, возникает вопрос - что такое прямая в физическом мире. Иначе говоря: "Как построить в действительности прямую линию? ". 8

Пространство "Как построить в действительности прямую линию? ". Ответ прост - возьмем луч света. Но Луч света - прямая линия, только в однородном пространстве. 9

Пространство Луч света - прямая линия, только в однородном пространстве. Миражи в Аравийской пустыне над дорогой 10

n Пространство В XIX веке Н. И. Лобачевский (1792 -1856) и Я. Бойаи (18021860) показали, что можно построить замкнутую геометрическую систему, в которой через заданную точку может проходить несколько прямых, параллельных заданной. 11

Пространство n n n Примерно тогда же появилась геометрия Г. Ф. Б. Римана (1826 -1866) - геометрия на сфере. В ней не может существовать ни одной прямой, параллельной заданной. Прямые здесь определяются как линии, проходящие через полюса сферы. 12

Пространство Как же все-таки определить, в каком пространстве мы живем, какой геометрией оно описывается? Евклида? Лобачевского? Римана? Какой-то еще? 13

Пространство Возможно, что проще всего это сделать, измерив углы большого треугольника n в геометрии Евклида сумма углов треугольника 1800, n в геометрии Римана больше 1800, n в геометрии Лобачевского - меньше 1800. 14

n n больших базах были проведены К. Ф. Гауссом (1777 -1855). Он с помощью геодезических приборов измерял углы треугольника, построенного на вершинах гор при расстоянии между ними около 100 км. Отклонений суммы углов от 180 0 не было обнаружено. Пространство 15

Пространство n Лобачевский измерял углы треугольника, основание которого совпадало с диаметром земной орбиты, а вершина находилась в месте положения яркой звезды (Сириуса). n Отклонений суммы углов от 180 0 не было обнаружено. 16

n n Пространство Выберем какой-то иной треугольник, произведем аналогичные описанным измерения и обнаружим, что сумма углов отличается от 180 0. Можем ли мы тогда сделать однозначный вывод: «Пространство не подчиняется геометрии Евклида» ? Нет Нам ведь известно, что лучи света не прямые линии 17

пространство евклидово, а частицы двигаются криволинейно только под действием сил. Пространство n В общей теории относительности Эйнштейна предполагается, что единое пространствовремя неевклидово, частицы перемещаются вдоль путей, которые при заданной кривизне пространства совпадают с кратчайшими расстояниями между любыми двумя точками. 18

n n Пространство Однако результаты обеих теорий в большинстве случаев совпадают. Это доказывает условность выбора точки зрения на геометрию пространства. Выбор — плод человеческой мысли. Наблюдаемые явления природы определяют адекватность выбора 19

Пространство Условность выбора точки зрения на геометрию пространства Географические карты 20

Пространство Линия имеет размерность (число координат, необходимых для n Способы описания пространства и объектов в пространстве определения положения лежащей на этой фигуре точки) 1, развиваются и сегодня плоскость – размерность 2, тело – размерность 3. Можем ли мы представить себе объект с размерностью 3/2? 21

Пространство n В 1919 году немецкий математик Ф. Хаусдорф (1868 -1942) математически строго определил пространство с нецелой размерностью. n В 1975 году математик Ш. Мандельбройт (1899 -1983) назвал пространства с дробной размерностью фрактальными (от англ. «fraction» – дробь). 22

Пространство Х. Кох (1870 -1924) 23

Пространство 24

бесконечностью и самоподобием снежинки Кох, писал в 1905 году: Пространство «Если бы она была одарена жизнью, то можно было бы лишить ее жизни, только уничтожив кривую в целом, в противном случае она возрождалась бы снова из глубины своих треугольников, как это делает жизнь во Вселенной» . 25

не гладкая, и молния не распространяется по прямой. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности. Существование этих структур бросает нам вызов в виде трудной задачи изучения тех форм, которые Евклид отбросил как бесформенные, - задачи исследования морфологии аморфного…» . Ш. Мандельбройт Пространство 26

Пространство Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы текста неразветвляющееся бесконечное дерево, тождественные самим себе с любой итерации ( «У попа была собака…» , «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится…» , «Ложно утверждение, что истинно утверждение, что ложно утверждение…» ) 27

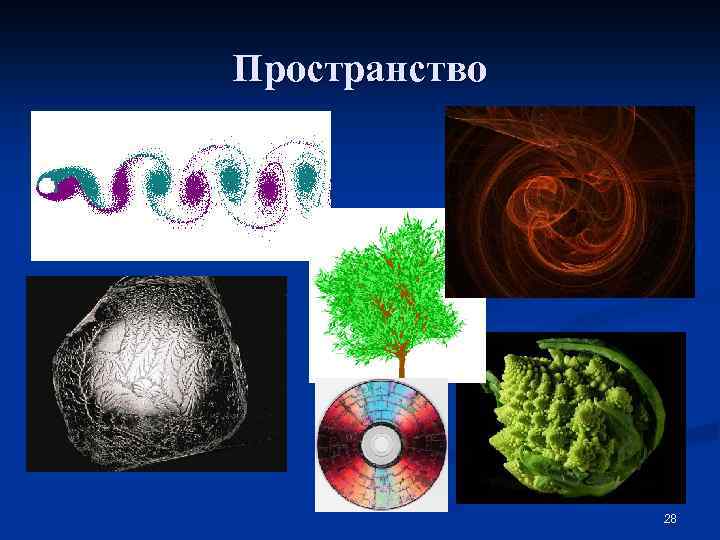Пространство 28

точками. Ими могут быть геометрические фигуры, функции, состояния физической системы и т. д. (Математика. Большой энциклопедический словарь). Пространство Физический энциклопедический словарь дает следующее определение пространства : «…пространство выражает порядок сосуществования отдельных объектов, время – порядок смены явлений…» 29

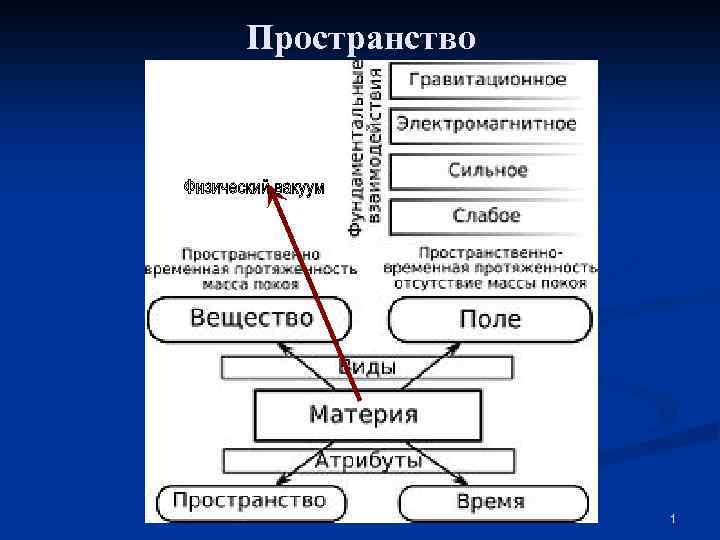
Вариант 1. Какие виды фундаментальных взаимодействий Вам известны Пространство Вариант 2. Дайте определение понятия «материя» Следующая лекция «Время» 30