Пространственно-локализованные структуры – осциллоны – в атомном БЭК в оптической решётке
Атомный БЭК в решётке Уравнение Гросса-Питаевского Условие нормировки: – внешний потенциал – оптическая решётка – объём структуры в размерности D – атом-атомное рассеяние в D-мерной структуре 1
Уравнение для огибающей Условие ортонормированности: Разложение ВФ: медленная огибающая Уравнение для 3 получаем блоховская функция -методом. Представляем в виде . Нормированная эффективная масса Выполняем разложение В точке первой ЗБ для двух первых энергетических зон (n=1, 2): Управляющее уравнение для 2
Дисперсия атомов БЭК в решётке Плоская волна: Дисперсионные соотношения: Изочастотная поверхность Поле Клейна-Гордона Поле Хиггса 3
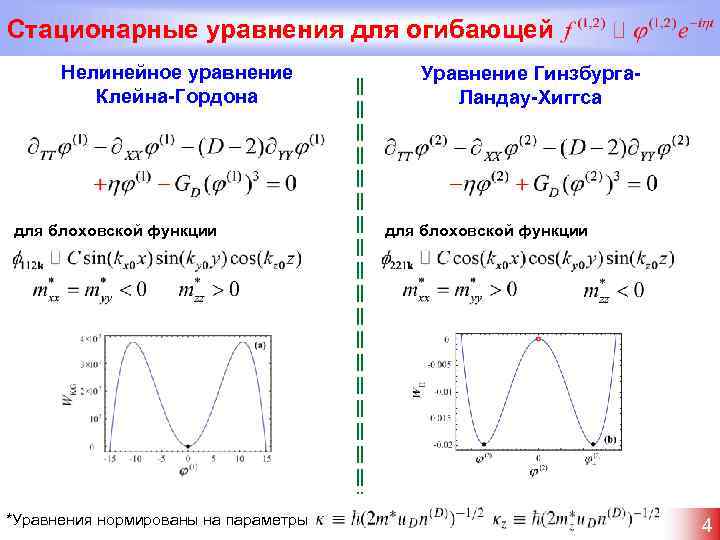
Стационарные уравнения для огибающей Нелинейное уравнение Клейна-Гордона для блоховской функции *Уравнения нормированы на параметры Уравнение Гинзбурга. Ландау-Хиггса для блоховской функции 4
Пространственно-локализованные структуры в поле Клейна-Гордона: осциллоны Решение НУКГ ищем методом растянутых переменных (теория возмущений) [N. Bogolyubov, Yu. A. Mitropol'skil, 1963] Координаты: – малый параметр задачи – амплитуда решения; Осциллоны в размерности D=1+1 “Квантованная” энергия осциллона – “квантовое число” Плотность вероятности осциллонов 5
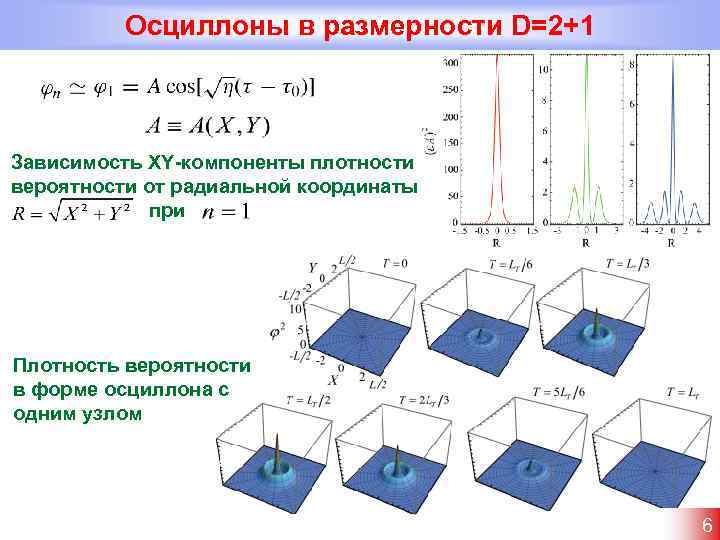
Осциллоны в размерности D=2+1 Зависимость XY-компоненты плотности вероятности от радиальной координаты при Плотность вероятности в форме осциллона с одним узлом 6
Осциллоны в поле Хиггса: размерность D=1+1 Уравнение Гинзбурга-Ландау-Хиггса Решение с малым возмущением: где – стационарное решение в форме кинка – осциллирующая по T добавка 1) Осциллон Хиггса 2) Масса кинка: Возмущение кинка 7
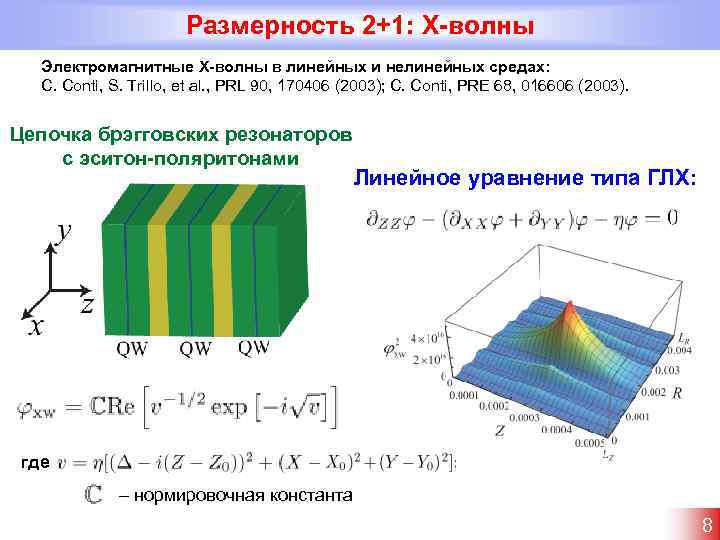
Размерность 2+1: X-волны Электромагнитные X-волны в линейных и нелинейных средах: C. Conti, S. Trillo, et al. , PRL 90, 170406 (2003); C. Conti, PRE 68, 016606 (2003). Цепочка брэгговских резонаторов с эситон-поляритонами Линейное уравнение типа ГЛХ: где – нормировочная константа 8
Заключение 1. Предложены механизмы создания атомных сред с гиперболической дисперсией за счёт управления величиной и знаком эффективной массы атомов в первой зоне Бриллюена. 2. Найдены локализованные стационарные решения нелинейного уравнения Клейна-Гордона в конечных структурах размерности 1+1 и 2+1 в форме осциллонов. 3. Найдены локализованные решения уравнения Гинзбурга-Ландау-Хиггса в конечной структуре размерности 1+1 в форме кинка с малым возмущением – осциллона Хиггса, обладающего эффективной массой. 4. Найдены решения линейного уравнения Гинзбурга. Ландау-Хиггса в конечной структуре размерности 2+1 в форме X-волн.
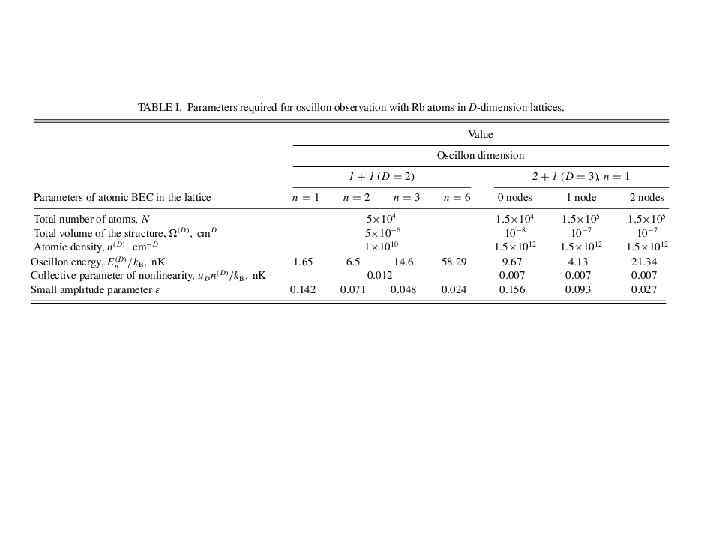
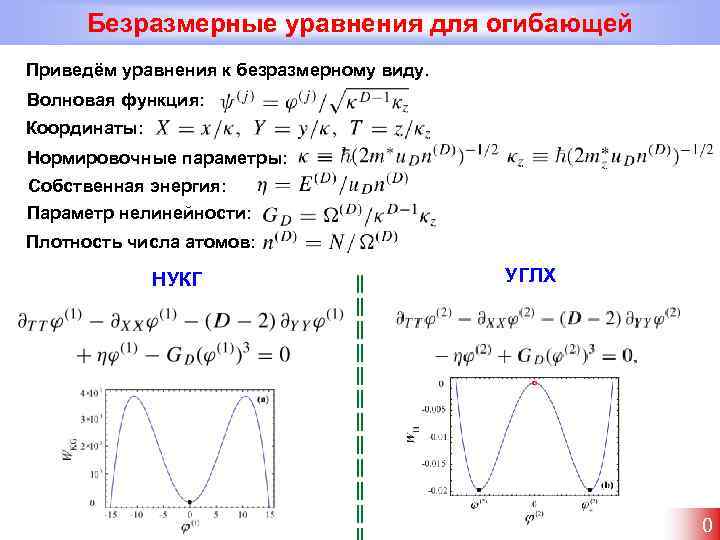
Безразмерные уравнения для огибающей Приведём уравнения к безразмерному виду. Волновая функция: Координаты: Нормировочные параметры: Собственная энергия: Параметр нелинейности: Плотность числа атомов: НУКГ УГЛХ 0
Скачать презентацию Пространственно-локализованные структуры осциллоны в атомном БЭК
доклад.pptx