Скачать презентацию Просторово частотні та спектральні методи і алгоритми
Lecture_5_filtering_color_transform_fusion_amp.ppt
- Количество слайдов: 31
Просторово – частотні та спектральні методи і алгоритми обробки даних ДЗЗ
План лекції Фільтрація зображень Аналіз кольорової композиції зображень Методи злиття даних Аналіз зображень за методом головних компонент
Фільтрація є дуже важливою частиною обробки цифрових зображень. Фільтрація базується на аналізі близькості значень характеристик пікселів і тим відрізняється від простих точкових операцій. Фільтрація базується на вивченні та трансформуванні просторового скручування (перетворенні функції згортки) ансамблю різночастотних хвиль, що складають спектральний відгук від об’єктів спостереження
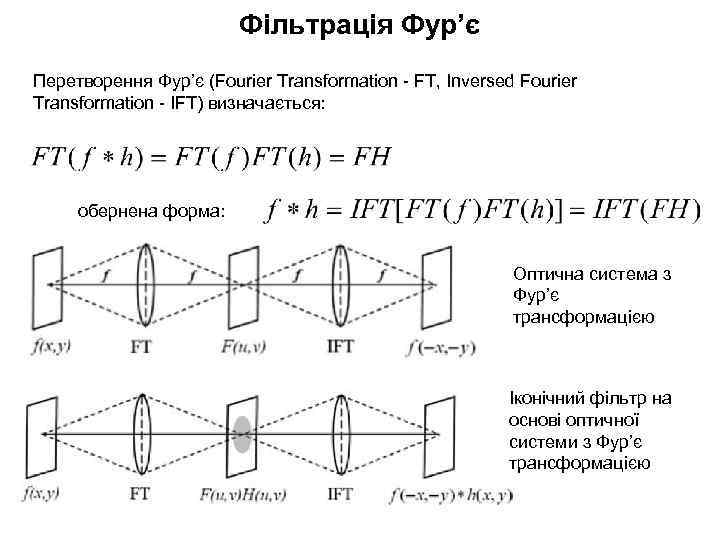Фільтрація Фур’є Перетворення Фур’є (Fourier Transformation - FT, Inversed Fourier Transformation - IFT) визначається: обернена форма: Оптична система з Фур’є трансформацією Іконічний фільтр на основі оптичної системи з Фур’є трансформацією
Фільтрація Фур’є також можна записати: Класична фільтрація базується на теоремі згортці, яка визначає властивості Фур’є – фільтрації для оптичних систем – згортку розподілу пікселів зображення f (x, y) та функцію точкового розподілу (point spread function – PSF, або гістограму) зображення h (x, y) як: Вхідне зображення f(x, y) Частотний спектр Фур’є F (u, v)
Низькочастотна фільтрація (low-pass filters / smoothing) або згладжування використовуються для видалення з цифрових зображень високочастотних компонент спектру і таким чином, видалення шуму, при цьому, однак, втрачається детальність. Основні фільтри: фільтр Гауса, медіанний фільтр, фільтр основної модуляції, умовний згладжувальний фільтр тощо Фільтр Гауса визначається через стандартне відхилення розподілу фототону зображення σ:
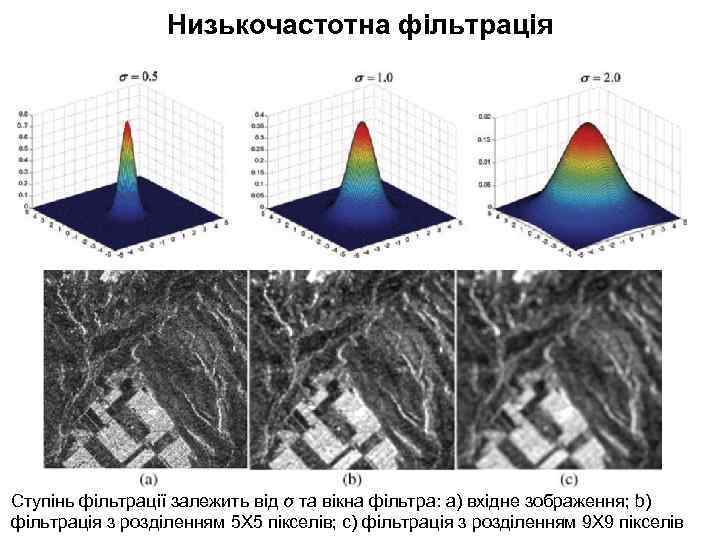Низькочастотна фільтрація Ступінь фільтрації залежить від σ та вікна фільтра: а) вхідне зображення; b) фільтрація з розділенням 5 Х 5 пікселів; c) фільтрація з розділенням 9 Х 9 пікселів
Високочастотна фільтрація (high-pass filters / edge enhancement) або підкреслювання країв використовується для видалення низькочастотної складової спектру цифрового зображення і, таким чином, підкреслювання ліній зміни контрастів. Відповідно, цій метод базується на аналізі першої (градієнтна фільтрація) і другої (фільтр Лапласа) похідних розподілу фототону зображень. градієнтний фільтр: де ,
Високочастотна фільтрація: градієнтний фільтр Алгоритм градієнтної фільтрації базується на розрахунку простої різниці між показниками розподілу щільності фотонону розрахункового пікселу і сусідніх пікселів у вікні фільтрації, віднесеної до відстаней між ними: Вхідне зображення а), і результати градієнтної фільтрації: b) gx, c) gy
Високочастотна фільтрація: фільтр Лапласа Фільтр Лапласа враховує всі наявні різниці між розрахунковим пікселом f(x, y) та його оточенням у вікні фільтрації δx, δy: Вхідне зображення а), b) – результат застосування фільтру Лапласа, с) – гістограма фільтрованого зображення
Локальне збільшення контрасту Ця процедура базується на значенні статистичних показників розподілів щільності фототону зображень. В найпростішому випадку використовується середнє значення по віконцю фільтрації та загальне середнє m 0: Існують інші алгоритми, що використовують додаткові статистичні показники (стандартне відхилення σ) та можливості параметричного контролю (параметр α):
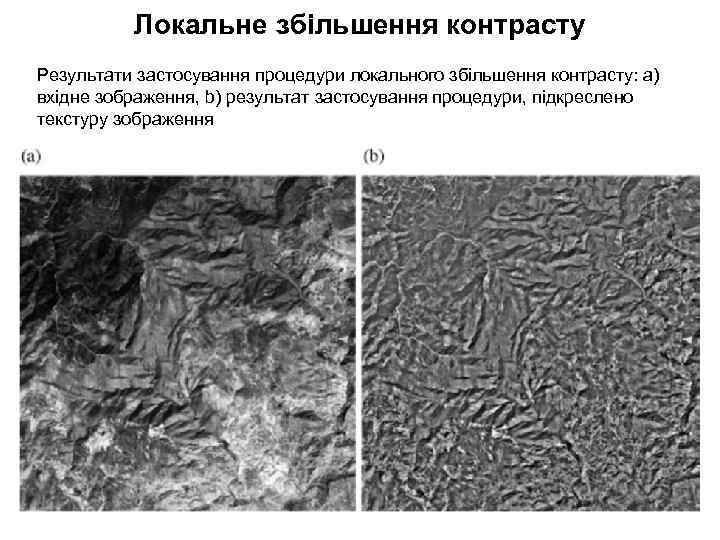Локальне збільшення контрасту Результати застосування процедури локального збільшення контрасту: а) вхідне зображення, b) результат застосування процедури, підкреслено текстуру зображення
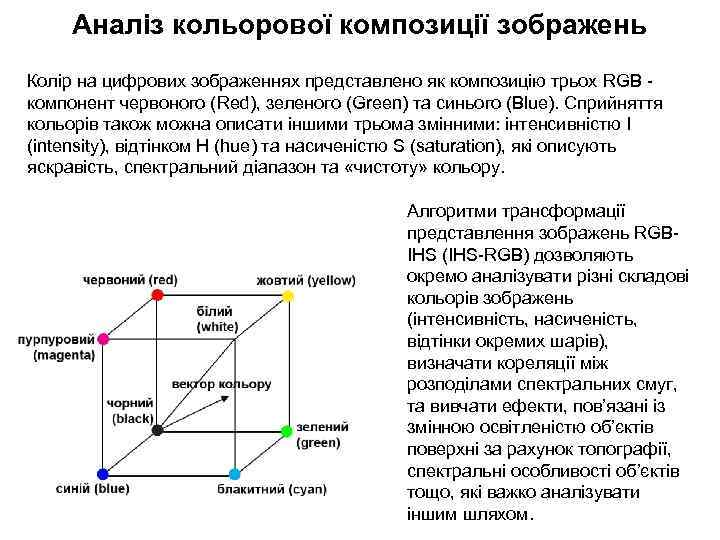Аналіз кольорової композиції зображень Колір на цифрових зображеннях представлено як композицію трьох RGB компонент червоного (Red), зеленого (Green) та синього (Blue). Сприйняття кольорів також можна описати іншими трьома змінними: інтенсивністю I (intensity), відтінком H (hue) та насиченістю S (saturation), які описують яскравість, спектральний діапазон та «чистоту» кольору. Алгоритми трансформації представлення зображень RGBIHS (IHS-RGB) дозволяють окремо аналізувати різні складові кольорів зображень (інтенсивність, насиченість, відтінки окремих шарів), визначати кореляції між розподілами спектральних смуг, та вивчати ефекти, пов’язані із змінною освітленістю об’єктів поверхні за рахунок топографії, спектральні особливості об’єктів тощо, які важко аналізувати іншим шляхом.
Аналіз кольорової композиції зображень Перетворення кольорового представлення цифрових зображень (RGB-IHS або IHS-RGB трансформація) визначається відповідно до:
Аналіз кольорової композиції зображень Основні методи перетворення кольорів: - розширення автокореляційної функції IHS (спрямована на збільшення об’єму кластеру зображення з максимальними значеннями інтенсивності), - метод лінійного розширення крос-кореляційних функцій (direct saturation stretch - DSS) безпосереднього RGB-IHS перетворення, - метод створення композитного зображення відтінків RGB зображення (HRGB – hue RGB color compotes), що дозволяє більш ефективно редукувати топографічні ефекти і відображати спектральні розподіли з великої кількості спектральних смуг існує ще кілька варіантів аналізу композиції кольорів і, відповідно, алгоритмів їхнього розподілу для різних задач
Розширення автокореляційної функції IHS Композиція зображень супутника Landsat сенсору ETM: a) вхідне RGB зображення (смуги 5, 3, 1), b) після процедури підвищення контрасту BCET, c) після процедури розширення автокореляційної функції IHS, d) після застосування DDS алгоритму
Лінійне розширення крос-кореляційних функцій Композиція зображень супутника EOS Terra-1 сенсору ASTER: a) вхідне RGB зображення (смуги 3, 2, 1) після процедури підвищення контрасту BCET, b), c), d) зображення після застосування DDS алгоритму з різними значеннями змінних (ахроматичний фактор k=0, 3, 0, 5, 0, 7 відповідно)
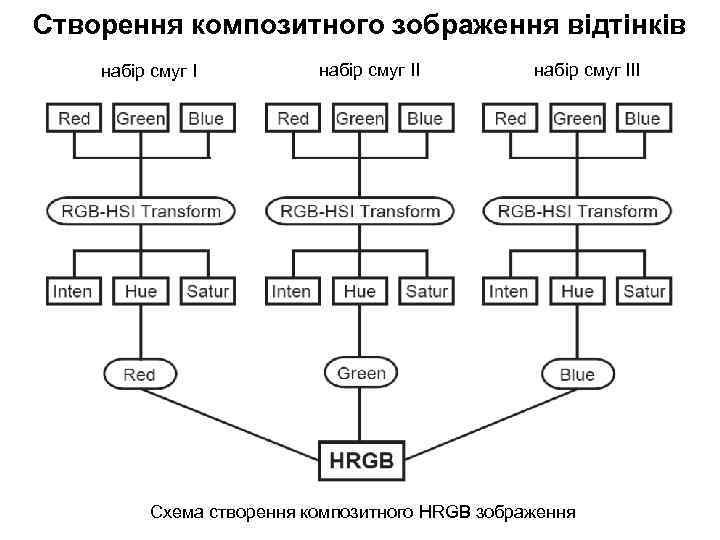Створення композитного зображення відтінків набір смуг ІІІ Схема створення композитного HRGB зображення
Створення композитного зображення відтінків Композиція зображень, отримані за допомогою сенсору авіаційного базування ATM (Airborne Thematic Mapper): a) HRGB композиція: канал R – відтінки отримані із смуг 10, 9, 8, канал G – відтінки, отримані із смуг 7, 6, 5, канал B – відтінки, отримані із 4, 3, 2, b) звичайне RGB зображення, скомбіноване із смуг 8, 5 і 2
Методи злиття даних ЗЛИТТЯ ДАНИХ - процедура оброблення системи даних, що отримуються з різних джерел, яка базується на законах сінергетики. Система даних включає як безпосереднє дані, так і засоби управління даними, і розглядається як відкрита система в нерівноважному стані. Алгоритмічно процедура З. д. носить послідовний, ітеративний характер, її ціллю є підвищення ступеню узгодженості та упорядкованості даних і, таким чином, певне зменшення ентропії системи Злиття зображень, в такому випадку можна розглядати у більш звуженому сенсі, як створення нового зображення на базі інтеграції набору зображень з різних джерел з різними просторовими та/або спектральними характеристиками
Методи злиття даних: RGB-IHS перетворення Злиття зображень супутників Landsat TM і SPOT: a) вхідне RGB - зображення Landsat TM (смуги 5, 4, 1) після процедури підвищення контрасту BCET, b) панхроматичне зображення SPOT Pan, c) синтезоване IHS зображення Landsat TM (смуги 5, 4, 1) та SPOT Pan, d) синтезоване зображення після застосування алгоритму модуляції інтенсивності, e) синтезоване зображення після застосування алгоритму модуляції інтенсивності із згладжуванням (SFIM) з розміром вікна фільтрації 5 Х 5, f) синтезоване зображення після застосування SFIM з розміром вікна фільтрації 3 Х 3
Методи злиття даних: модуляція інтенсивності Метод базується на визначенні вектору інтенсивності Р вихідного зображення по відношенню до кольорових компонент вхідних зображень (і, таким чином, наближається до IHS методик):
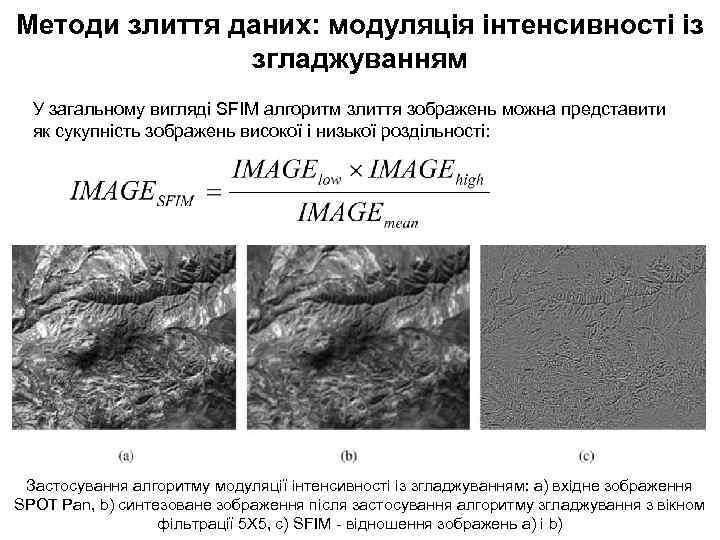Методи злиття даних: модуляція інтенсивності із згладжуванням У загальному вигляді SFIM алгоритм злиття зображень можна представити як сукупність зображень високої і низької роздільності: Застосування алгоритму модуляції інтенсивності із згладжуванням: а) вхідне зображення SPOT Pan, b) синтезоване зображення після застосування алгоритму згладжування з вікном фільтрації 5 Х 5, с) SFIM - відношення зображень а) і b)
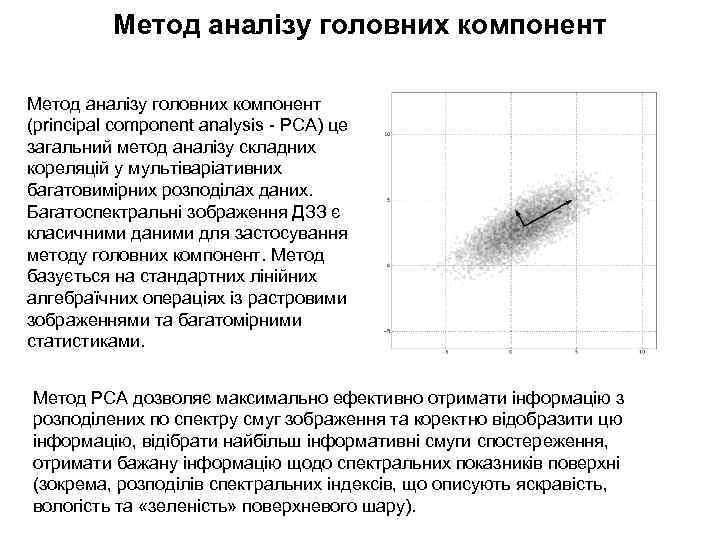Метод аналізу головних компонент (principal component analysis - PCA) це загальний метод аналізу складних кореляцій у мультіваріативних багатовимірних розподілах даних. Багатоспектральні зображення ДЗЗ є класичними даними для застосування методу головних компонент. Метод базується на стандартних лінійних алгебраїчних операціях із растровими зображеннями та багатомірними статистиками. Метод PCA дозволяє максимально ефективно отримати інформацію з розподілених по спектру смуг зображення та коректно відобразити цю інформацію, відібрати найбільш інформативні смуги спостереження, отримати бажану інформацію щодо спектральних показників поверхні (зокрема, розподілів спектральних індексів, що описують яскравість, вологість та «зеленість» поверхневого шару).
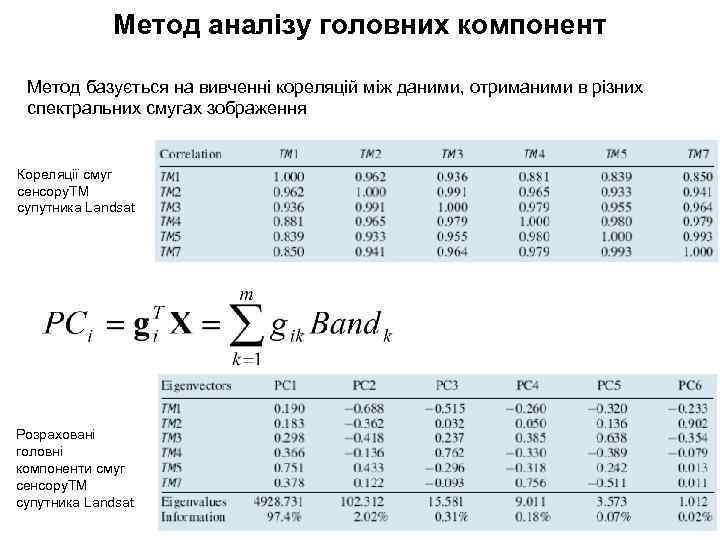Метод аналізу головних компонент Метод базується на вивченні кореляцій між даними, отриманими в різних спектральних смугах зображення Кореляції смуг сенсору. TM супутника Landsat Розраховані головні компоненти смуг сенсору. TM супутника Landsat
Метод аналізу головних компонент розподіл головних компонент зображення сенсору TM супутника Landsat
Вибірковий аналіз головних компонент Вибірковий аналіз (SPCA) включає картування спектрального контрасту (FPCS) та приведення кольорового спотворення (в тому числі – зменшення хроматичних аберацій) Зображення Landsat TM: а) RGB композиція з РС 4, РС 3, РС 5, b) SPCA композиція для зменшення хроматичних аберацій, с) SPCA композиція для картування спектрального контрасту, d) FPCS композиція для картування оксиду заліза (червоний), рослинності (зелений) і глини (синій)
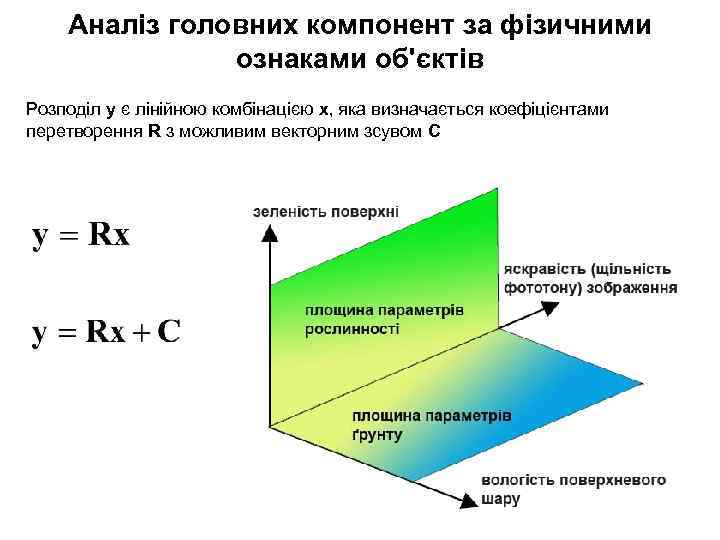Аналіз головних компонент за фізичними ознаками об'єктів Розподіл у є лінійною комбінацією х, яка визначається коефіцієнтами перетворення R з можливим векторним зсувом С
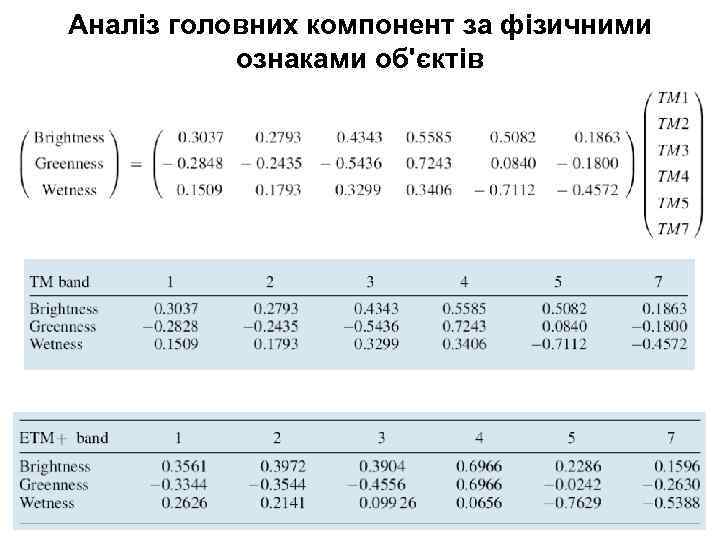Аналіз головних компонент за фізичними ознаками об'єктів
Статистичні методи вибору спектральних смуг На основі методу головних компонент розроблено низку методик об’єктно – орієнтованих алгоритмів визначення оптимальних наборів спектральних каналів на основі optimal index factor (OIF): де SD – стандартні відхилення, r коефіцієнти кореляції для смуг i, j. коефіцієнти кореляції визначаються через варіації в смугах i, j:
