Простір товарів Вектор цін Під товаром розуміють

Простір товарів. Вектор цін.

Під товаром розуміють деяку продукцію або послугу, яка надходить на ринок для продажу в певний час і в певному місці. Вважатимемо, що маємо п різних товарів. Обсяг і-того товару позначимо через , і = 1, 2, . . . , п.

Тоді деякий набір цих товарів можна записати у вигляді вектора x = (x 1, x 2, …, x n), тобто x є п-вимірним вектором. З економічних міркувань розглядатимемо тільки такі набори товарів, у яких компоненти x i ≥ 0 для довільного і = 1, 2, . . . , п. Множину всіх наборів товарів називають простором товарів С. Ця множина є простором тому, що в ній можна додавати два довільних набори й множити будь-який набір товарів на довільне невід’ємне число.

n Вважаємо, що кожен товар має певну ціну. Всі ціни строго додатні. Нехай ціна одиниці і-того товару становить р і , і = 1, 2, . . . , п. Тоді вектор р = (р 1, р 2 , . . . , р п ) називають вектором цін. Для набору товарів x = (x 1, x 2, …, x n) розглянемо вектор відповідних цін р = (р 1, р 2 , . . . , р п ). Скалярний добуток цих векторів

р ∙ х = р1∙ х1 + р2 ∙ х 2 +. . . + рп ∙ х п є числом, яке визначає ціну набору товарів і позначається с(х).

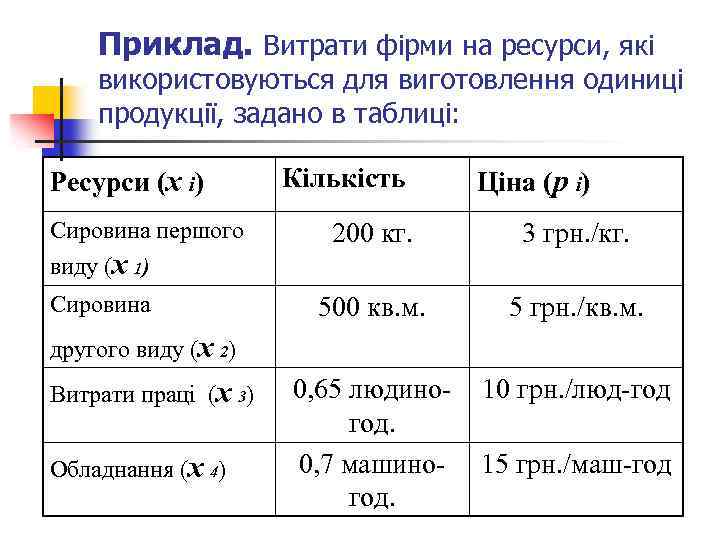Приклад. Витрати фірми на ресурси, які використовуються для виготовлення одиниці продукції, задано в таблиці: Ресурси (x i) Сировина першого виду (x 1) Сировина Кількість Ціна (р i) 200 кг. 3 грн. /кг. 500 кв. м. 5 грн. /кв. м. 0, 65 людиногод. 0, 7 машиногод. 10 грн. /люд-год другого виду (x 2) Витрати праці (x 3) Обладнання (x 4) 15 грн. /маш-год

Визначити ціну всіх ресурсів, що використовуються фірмою для виготовлення одиниці продукції. n Розв’язання. Введемо вектор витрат ресурсів на одиницю продукції x = ( 200; 500; 0, 65; 0, 7 ) та вектор цін одиниць відповідних ресурсів р = (3; 5; 10; 15). Вартість усіх ресурсів, що використовуються для виготовлення одиниці продукції, буде скалярним добутком цих векторів. Тому

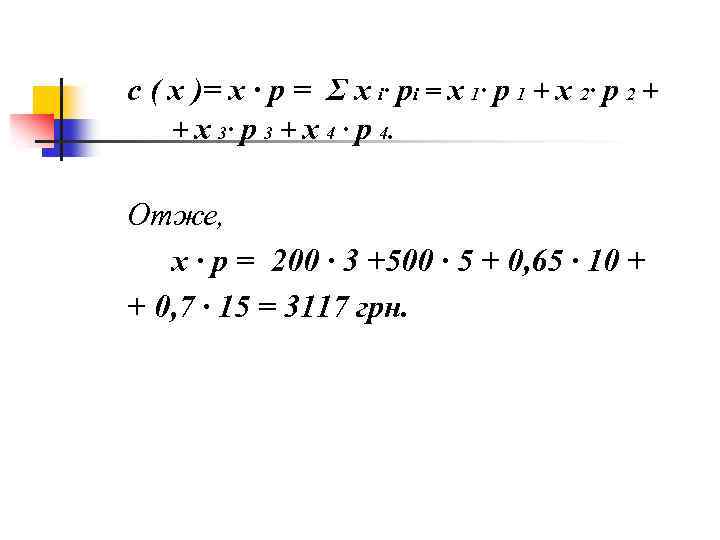с ( х )= х ∙ р = Σ x i∙ рі = х 1∙ р 1 + х 2∙ р 2 + + х 3∙ р 3 + х 4 ∙ р 4. Отже, х ∙ р = 200 ∙ 3 +500 ∙ 5 + 0, 65 ∙ 10 + + 0, 7 ∙ 15 = 3117 грн.

Приклад. Комерційний банк, що бере участь у будівництві багатоповерхових будинків на одному з масивів міста, одержав кредити від трьох комерційних банків. Кожен із них надав кредити в розмірі відповідно 200, 300, 400 тис. грн. під річну процентну ставку 40, 25 і 30 %. Визначити, яку суму треба заплатити за кредити наприкінці року.

Розв’язання. Розглянемо вектор кредитів x = (200; 300; 400) і вектор процентних ставок р = (1, 40; 1, 25; 1, 30 ). Простим розрахунком керівник комерційного банку може визначити, скільки потрібно заплатити наприкінці року за кредити взяті у банків: х ∙ р = 200 ∙ 1, 4 + 300 ∙ 1, 25 + 400 ∙ 1, 3 = 1175 тис. грн.

Моделі аналітичної геометрії 1. Модель рівноваги ринку Розглянемо просту математичну модель рівноваги ринку, в якій основними є співвідношення між двома величинами : ціною одиниці товару p та обсягом товару на ринку q.

В основу зазначеної математичної моделі покладено просту ідею: розглянути ціну одиниці товару p та обсяг товару q як упорядковану пару чисел (p, q) і поставити їй у відповідність на площині точку з координатами (p; q ). Через p позначимо вісь абсцис, а через q – вісь ординат. Наприклад, пара (7; 2000) відповідає ситуації, коли 2000 одиниць товару можна продати за ціною 7 грн. за одиницю.

Візьмемо деякий товар. За даної ціни p за одиницю товару через s (p) позначимо число одиниць товару, які продавці на ринку пропонують для продажу. Функцію s = s(p) називають функцією пропозиції товару. Через q (p) позначимо число одиниць товару, що покупці бажають купити. Функцію q= q (p) називають функцією попиту на товар. З економічних міркувань функція пропозиції s= s(p) зростаюча, а функція попиту q= q (p) спадна.

Означення. Ціну , за якої попит на певний товар дорівнює пропозиції цього товару на ринку, називають рівноважною ціною. Тобто за рівноважної ціни p* виконується рівність s (p*) = q(p*). Точку Е (p*; q*) називають точкою рівноваги. Рис. 1.

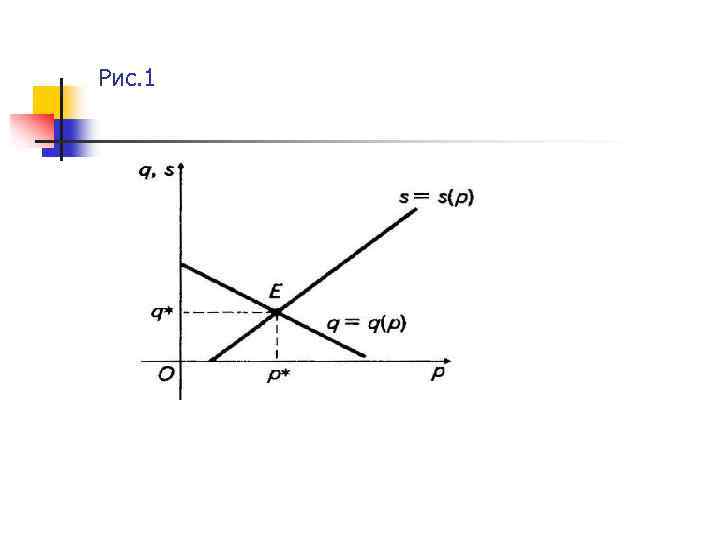Рис. 1

Розглянемо задачу. Нехай задано лінійні функції s(p) = bp – a і q(p) = c – dp, де a, b, c, d – додатні числа; ф-ія s = s(p) визначає пропозицію, ф-ія q = q (p) – попит на певний товар ринку. Потрібно знайти рівноважну ціну p*.

Розв'язання. Якщо відсутні всілякі податки, то рівноважна ціна визначається як розв’язок рівняння s (p*) = q(p*) або системи лінійних рівнянь

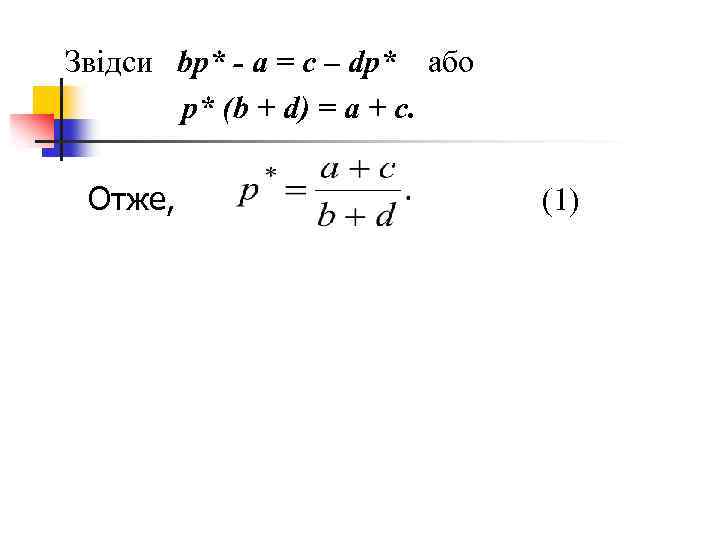Звідси bp* - a = c – dp* або p* (b + d) = a + c. Отже, (1)

Приклад. Нехай задано функцію попиту q = - 5 p + 40 функцію пропозиції s= Знайти точку рівноваги. Розв’язання. Координати точки рівноваги Е (p*; q*) задовольняють умову рівноваги s* = q*, тобто звідки p* = 4, а s* = q* = 40 – 5 p*= 20. Отже, шукана точка рівноваги – це точка Е (4; 20). Рис. 2.

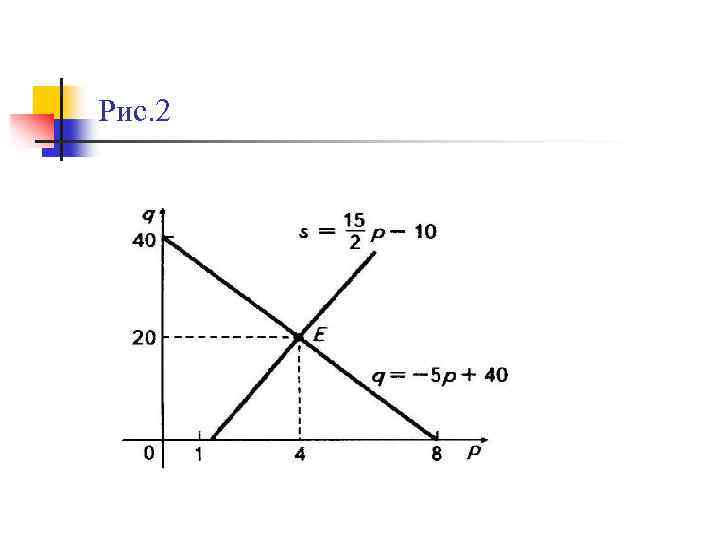Рис. 2

Приклад. Припустимо, що уряд деякої країни встановив акцизний податок Т за одиницю товару, причому цей податок є фіксованим числом, а не процентом від продажної ціни. Скориставшись даними прикладу. (функція попиту q = 40 – 5 p, функція пропозиції s = рівноважна ціна p* = 4). Визначити як зміняться при цьому рівноважна ціна та обсяг товару

Розв’язання. Якщо уряд установить акцизний податок Т за одиницю товару, то функція пропозиції зміниться й задаватиметься співвідношенням а функція попиту залишиться незмінною. Тоді нову точку рівноваги можна визначити з умови рівноваги , тобто.

Отже, нова рівноважна ціна , а відповідний обсяг товару . Дістали нову точку рівноваги . Наприклад, якщо податок Т = 1 грн. за одиницю продукції, то рівноважна ціна збільшиться від 4 до 4, 6 грн. , а обсяг товару (пропозиція) зменшиться з 20 до 17, тобто обсяг одиниць товару для продажу зменшується на 3 Т, а ціна збільшується на

Розглянемо загальнішу ситуацію, коли функції попиту q = c – dp і пропозиції s = bp – a лінійні ( a, b, c, d – деякі додатні числа). Якщо встановлено податок Т за одиницю товару, то нова ціна буде. Визначаємо нову точку рівноваги з умови , де , а. Тоді. Із цієї рівності знаходимо нову рівноважну ціну

Враховуючи результат попереднього прикладу та формулу (1), матимемо Отже, нова рівноважна ціна підвищується на Оскільки b > 0 і d > 0, то і