3_kurs_tatuzov_lecture_2.ppt
- Количество слайдов: 26
 Простейшие вероятностные модели Случайные величины Свойства и характеристики случайных величин Генерация псевдослучайных величин Примеры моделей
Простейшие вероятностные модели Случайные величины Свойства и характеристики случайных величин Генерация псевдослучайных величин Примеры моделей
 Случайные величины Определение термина Случайная величина: Случайная величина в теории вероятностей, величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями Число очков, выпадающее на верхней грани игральной кости, представляет собой случайную величину, принимающую значения 1, 2, 3, 4, 5, 6 с вероятностью 1/6 каждое Момент времени, когда происходит распад нестабильного ядра, представляет собой случайную величину, принимающую значения на интервале (0, ) с плотностью вероятностей
Случайные величины Определение термина Случайная величина: Случайная величина в теории вероятностей, величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями Число очков, выпадающее на верхней грани игральной кости, представляет собой случайную величину, принимающую значения 1, 2, 3, 4, 5, 6 с вероятностью 1/6 каждое Момент времени, когда происходит распад нестабильного ядра, представляет собой случайную величину, принимающую значения на интервале (0, ) с плотностью вероятностей
 Свойства случайных величин Математическое ожидание (момент второго порядка) для дискретной величины Математическое ожидание очков на игральной кости: для непрерывной величины Математическое ожидание времени, оставшегося до распада нестабильного ядра:
Свойства случайных величин Математическое ожидание (момент второго порядка) для дискретной величины Математическое ожидание очков на игральной кости: для непрерывной величины Математическое ожидание времени, оставшегося до распада нестабильного ядра:
 Свойства случайных величин Дисперсия (центральный момент второго порядка) для дискретной величины Дисперсия очков на игральной кости: для непрерывной величины Дисперсия времени, оставшегося до распада нестабильного ядра:
Свойства случайных величин Дисперсия (центральный момент второго порядка) для дискретной величины Дисперсия очков на игральной кости: для непрерывной величины Дисперсия времени, оставшегося до распада нестабильного ядра:
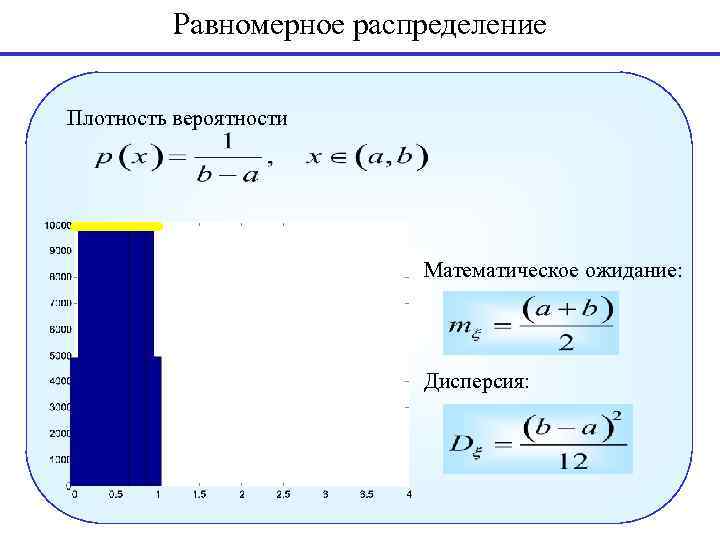 Равномерное распределение Плотность вероятности Математическое ожидание: Дисперсия:
Равномерное распределение Плотность вероятности Математическое ожидание: Дисперсия:
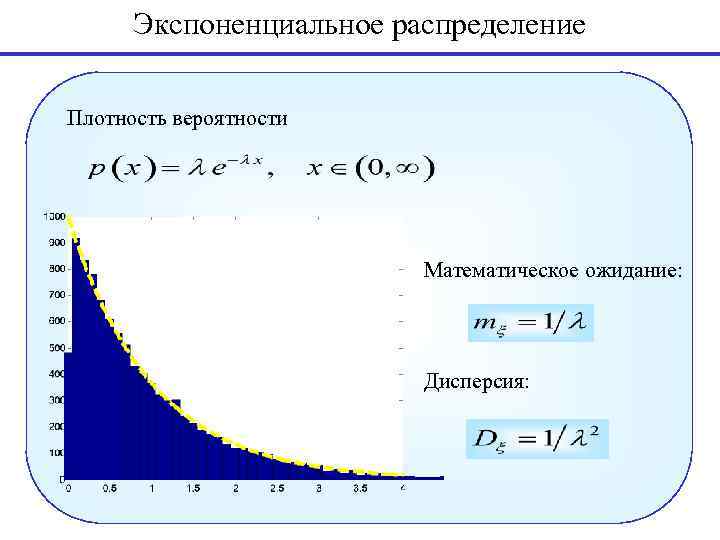 Экспоненциальное распределение Плотность вероятности Математическое ожидание: Дисперсия:
Экспоненциальное распределение Плотность вероятности Математическое ожидание: Дисперсия:
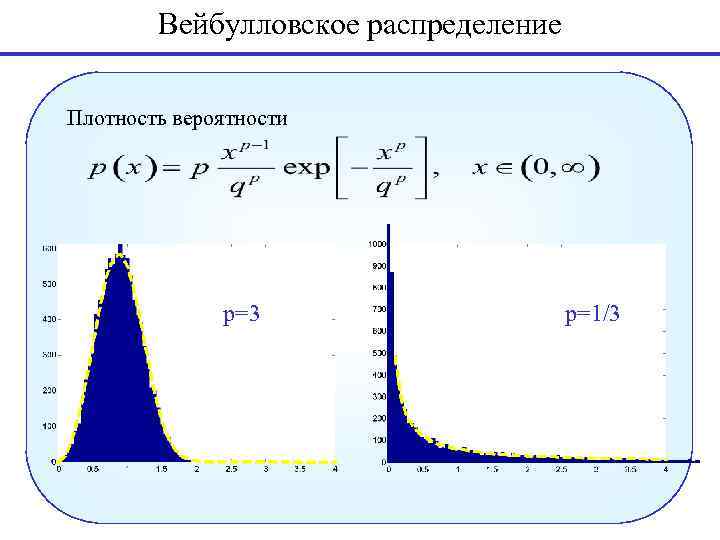 Вейбулловское распределение Плотность вероятности p=3 p=1/3
Вейбулловское распределение Плотность вероятности p=3 p=1/3
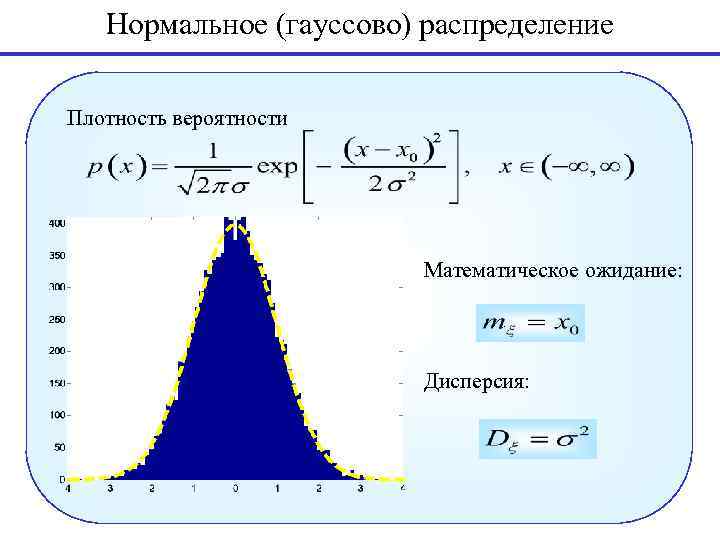 Нормальное (гауссово) распределение Плотность вероятности Математическое ожидание: Дисперсия:
Нормальное (гауссово) распределение Плотность вероятности Математическое ожидание: Дисперсия:
 Примеры простейших моделей Модель ожидания автобуса Необходимо оценить качество обслуживания пассажиров Формальная постановка Определить время ожидания автобуса Определить вероятность того, что за время T автобус прибудет Исходные условия и основные моделируемые факторы Автобусы прибывают на остановку с заданным фиксированным интервалом t Пассажир приходит на остановку в случайный момент времени Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе?
Примеры простейших моделей Модель ожидания автобуса Необходимо оценить качество обслуживания пассажиров Формальная постановка Определить время ожидания автобуса Определить вероятность того, что за время T автобус прибудет Исходные условия и основные моделируемые факторы Автобусы прибывают на остановку с заданным фиксированным интервалом t Пассажир приходит на остановку в случайный момент времени Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе?
 Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают на остановку с заданным фиксированным интервалом t Пассажир приходит на остановку в случайный момент времени Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе? tп t
Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают на остановку с заданным фиксированным интервалом t Пассажир приходит на остановку в случайный момент времени Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе? tп t
 Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, распределенными по равномерному закону (0, t) Пассажир приходит в момент отправления предыдущего автобуса Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе?
Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, распределенными по равномерному закону (0, t) Пассажир приходит в момент отправления предыдущего автобуса Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе?
 Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, распределенными по экспоненциальному закону с интенсивностью Пассажир приходит в момент отправления предыдущего автобуса Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе?
Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, распределенными по экспоненциальному закону с интенсивностью Пассажир приходит в момент отправления предыдущего автобуса Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе?
 Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, имеющими неизвестное распределение и среднее Пассажир приходит в момент отправления предыдущего автобуса Вопрос. Какова вероятность, что за время T пассажир уедет на автобусе? ?
Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, имеющими неизвестное распределение и среднее Пассажир приходит в момент отправления предыдущего автобуса Вопрос. Какова вероятность, что за время T пассажир уедет на автобусе? ?
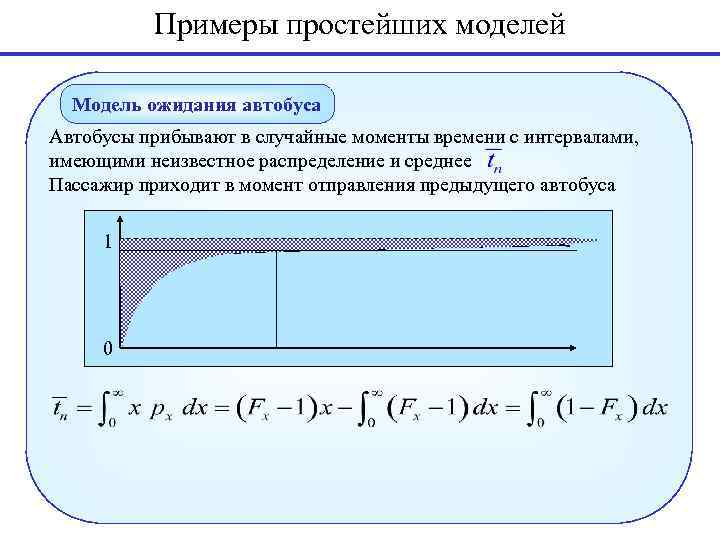 Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, имеющими неизвестное распределение и среднее Пассажир приходит в момент отправления предыдущего автобуса 1 0
Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, имеющими неизвестное распределение и среднее Пассажир приходит в момент отправления предыдущего автобуса 1 0
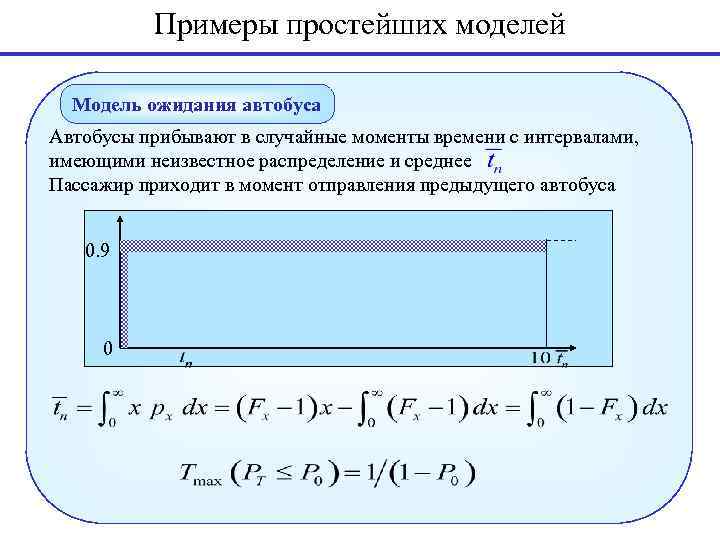 Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, имеющими неизвестное распределение и среднее Пассажир приходит в момент отправления предыдущего автобуса 0. 9 0
Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, имеющими неизвестное распределение и среднее Пассажир приходит в момент отправления предыдущего автобуса 0. 9 0
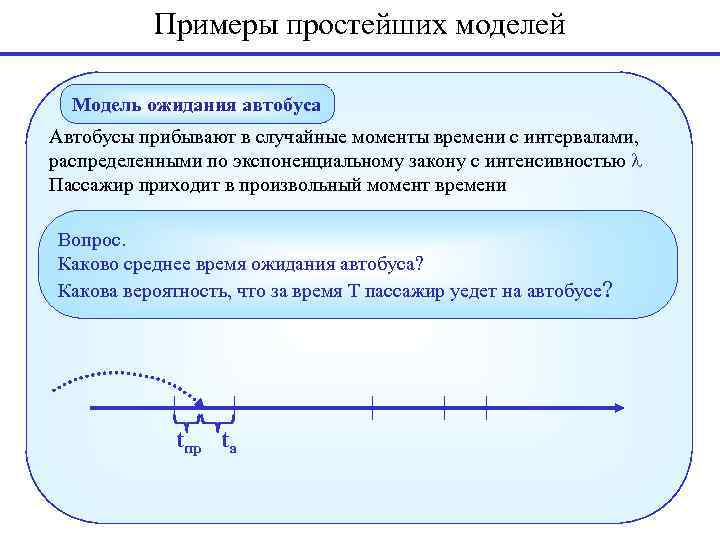 Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, распределенными по экспоненциальному закону с интенсивностью Пассажир приходит в произвольный момент времени Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе? tпр tа
Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, распределенными по экспоненциальному закону с интенсивностью Пассажир приходит в произвольный момент времени Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе? tпр tа
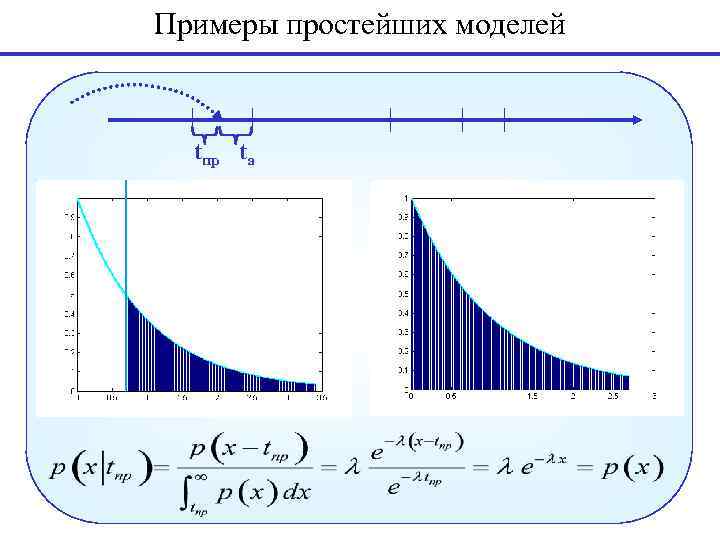 Примеры простейших моделей tпр tа
Примеры простейших моделей tпр tа
 Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, распределенными по экспоненциальному закону с интенсивностью Пассажир приходит в произвольный момент времени Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе? tпр tа
Примеры простейших моделей Модель ожидания автобуса Автобусы прибывают в случайные моменты времени с интервалами, распределенными по экспоненциальному закону с интенсивностью Пассажир приходит в произвольный момент времени Вопрос. Каково среднее время ожидания автобуса? Какова вероятность, что за время T пассажир уедет на автобусе? tпр tа
 Примеры простейших моделей Модель защиты объекта Необходимо оценить защищенность объекта от воздействия угроз Формальная постановка Определить вероятность того, что объект останется непораженным Исходные условия и основные моделируемые факторы Угрозы поступают на объект непрерывно с заданной интенсивностью Поток угроз простейший Меры защиты обеспечивают защиту от угроз с вероятностью p Вопрос. Какова вероятность, что за время T объект останется в сохранности?
Примеры простейших моделей Модель защиты объекта Необходимо оценить защищенность объекта от воздействия угроз Формальная постановка Определить вероятность того, что объект останется непораженным Исходные условия и основные моделируемые факторы Угрозы поступают на объект непрерывно с заданной интенсивностью Поток угроз простейший Меры защиты обеспечивают защиту от угроз с вероятностью p Вопрос. Какова вероятность, что за время T объект останется в сохранности?
 Примеры простейших моделей Модель защиты объекта Плотность вероятности для времени появления угрозы - вероятность противодействия угрозе Плотность вероятности для времени прохождения угрозы через систему защиты
Примеры простейших моделей Модель защиты объекта Плотность вероятности для времени появления угрозы - вероятность противодействия угрозе Плотность вероятности для времени прохождения угрозы через систему защиты
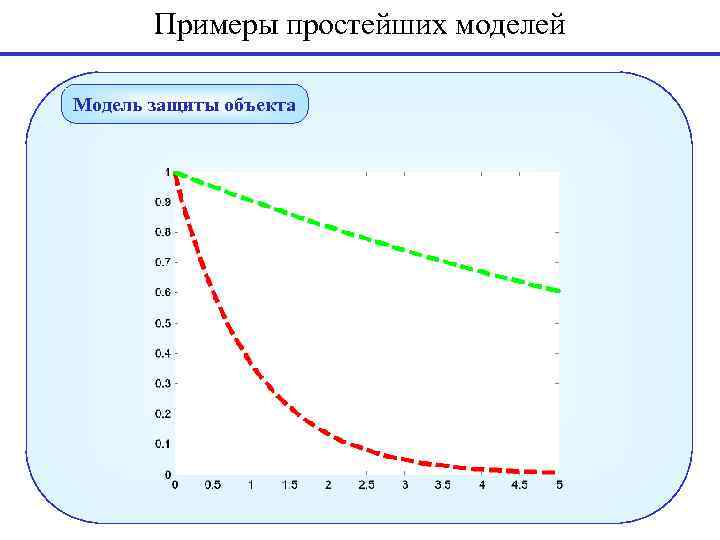 Примеры простейших моделей Модель защиты объекта
Примеры простейших моделей Модель защиты объекта
 Примеры простейших моделей Модель защиты объекта Необходимо оценить качество системы разведки опасных объектов Формальная постановка Определить вероятность того, что все опасные объекты за время T будут обнаружены Исходные условия и основные моделируемые факторы Объекты поступают на вход системы непрерывно с заданной интенсивностью . Поток угроз простейший Система обнаружения способнаружить объект с вероятностью p Вопрос. Какова вероятность, что за время T все объекты будут обнаружены?
Примеры простейших моделей Модель защиты объекта Необходимо оценить качество системы разведки опасных объектов Формальная постановка Определить вероятность того, что все опасные объекты за время T будут обнаружены Исходные условия и основные моделируемые факторы Объекты поступают на вход системы непрерывно с заданной интенсивностью . Поток угроз простейший Система обнаружения способнаружить объект с вероятностью p Вопрос. Какова вероятность, что за время T все объекты будут обнаружены?
 Примеры простейших моделей Модель защиты объекта Необходимо оценить качество системы разведки опасных объектов Формальная постановка Определить вероятность того, что все опасные объекты за время T будут обнаружены Исходные условия и основные моделируемые факторы Объекты поступают на вход системы непрерывно с заданной интенсивностью . Поток угроз простейший Система обнаружения состоит и M средств, каждое из которых способно обнаружить объект с вероятностью p. Объект считается обнаруженным, если K средств его увидели. Вопрос. Какова вероятность, что за время T все объекты будут обнаружены?
Примеры простейших моделей Модель защиты объекта Необходимо оценить качество системы разведки опасных объектов Формальная постановка Определить вероятность того, что все опасные объекты за время T будут обнаружены Исходные условия и основные моделируемые факторы Объекты поступают на вход системы непрерывно с заданной интенсивностью . Поток угроз простейший Система обнаружения состоит и M средств, каждое из которых способно обнаружить объект с вероятностью p. Объект считается обнаруженным, если K средств его увидели. Вопрос. Какова вероятность, что за время T все объекты будут обнаружены?
 Примеры простейших моделей Модель защиты объекта Необходимо оценить качество системы разведки опасных объектов Формальная постановка Определить вероятность того, что система обнаружения работает надежно Исходные условия и основные моделируемые факторы Объекты поступают на вход системы непрерывно с заданной интенсивностью . Поток простейший. Система обнаружения состоит и M средств, каждое из которых способно обнаружить объект с вероятностью p. Объект считается обнаруженным, если K средств его увидели. Вопрос. Какова вероятность, что за время T объекты будет обнаружено не менее 90% объектов?
Примеры простейших моделей Модель защиты объекта Необходимо оценить качество системы разведки опасных объектов Формальная постановка Определить вероятность того, что система обнаружения работает надежно Исходные условия и основные моделируемые факторы Объекты поступают на вход системы непрерывно с заданной интенсивностью . Поток простейший. Система обнаружения состоит и M средств, каждое из которых способно обнаружить объект с вероятностью p. Объект считается обнаруженным, если K средств его увидели. Вопрос. Какова вероятность, что за время T объекты будет обнаружено не менее 90% объектов?
 Примеры простейших моделей Модель надежности документов в wiki-энциклопедии Необходимо оценить качество wiki-энциклопедии Формальная постановка Определить вероятность того, что присутствующие в энциклопедии документы надежны Исходные условия и основные моделируемые факторы Документы поступают на вход системы непрерывно с заданной интенсивностью . Поступивший документ будет надежен с вероятностью p. Наблюдатели могут обнаружить ненадежный документ с вероятностью r и исправить его. Вопрос. Какова вероятность, что за время T все документы будут надежны?
Примеры простейших моделей Модель надежности документов в wiki-энциклопедии Необходимо оценить качество wiki-энциклопедии Формальная постановка Определить вероятность того, что присутствующие в энциклопедии документы надежны Исходные условия и основные моделируемые факторы Документы поступают на вход системы непрерывно с заданной интенсивностью . Поступивший документ будет надежен с вероятностью p. Наблюдатели могут обнаружить ненадежный документ с вероятностью r и исправить его. Вопрос. Какова вероятность, что за время T все документы будут надежны?
 Примеры простейших моделей Модель оценки качества деятельности ученых Необходимо оценить качество деятельности ученых Исходные условия и основные моделируемые факторы Каждый ученый имеет уровень квалификации Q. Он готовит публикации, научный уровень S которых случаен и имеет экспоненциальное распределение с параметром Q. Интенсивность публикаций равна Q. В зависимости от научного уровня, публикация может быть принята журналом. Импакт-фактор журнала, принявшего публикацию имеет экспоненциальное распределение с параметром S. Вопрос. Каков средний суммарный коэффициент публикаций ученого в зависимости от его уровня квалификации?
Примеры простейших моделей Модель оценки качества деятельности ученых Необходимо оценить качество деятельности ученых Исходные условия и основные моделируемые факторы Каждый ученый имеет уровень квалификации Q. Он готовит публикации, научный уровень S которых случаен и имеет экспоненциальное распределение с параметром Q. Интенсивность публикаций равна Q. В зависимости от научного уровня, публикация может быть принята журналом. Импакт-фактор журнала, принявшего публикацию имеет экспоненциальное распределение с параметром S. Вопрос. Каков средний суммарный коэффициент публикаций ученого в зависимости от его уровня квалификации?


